一个与3×3矩阵谱问题相关孤子方程的Darboux变换及精确解

张鑫，李新

（1.合肥科技职业学院基础部，安徽合肥230000；2.合肥师范学院实验实训中心，安徽合肥230601）

一个与3×3矩阵谱问题相关孤子方程的Darboux变换及精确解

张鑫1，李新2

（1.合肥科技职业学院基础部，安徽合肥230000；2.合肥师范学院实验实训中心，安徽合肥230601）

主要研究孤子方程的Darboux变换问题。文章从一个含两个位势的谱问题出发，构造其Darboux变换，并从在理论上给其证明，利用这种Darboux变换，就可以得到这组孤子方程多孤子解的一般表达式，以平凡解u=v=0作为种子解，得出精确解。通过Mathematica软件，绘制出其优美孤子图形。

孤子方程；Darboux变换；精确解；谱问题

日常生活中很多现象是由非线性规律来支配的。非线性科学已成为数学及整个自然科学研究的焦点，它主要包含三个核心问题：分形，混沌，孤子。孤子理论是以上三大核心问题之一[1-2]。寻求孤子方程的精确解一直是孤子理论探讨的重要问题。Darboux变换[3-6]是一种构造孤子方程显式解的非常有效的方法，它从孤子方程的一个平凡解（常称作种子解）出发能够得到孤子方程的非平凡精确解[7-9]。本文讨论孤子方程[10]

第一部分表达谱问题的Darboux变换，第二部分利用Darboux变换产生孤子方程的新精确解，并给出优美孤子图形。

1 Darboux变换

首先引入一个3×3矩阵谱问题以及与之相应的辅谱问题

其中U,V是以下矩阵形式：

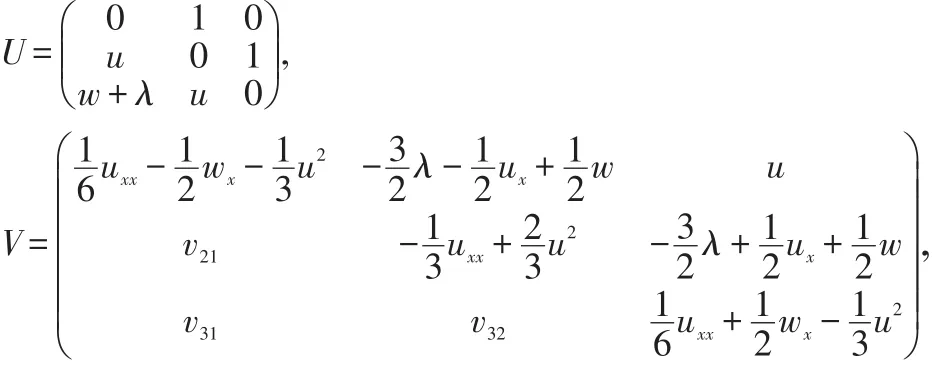
上式中的λ是等谱参数，u(x,t),w(x,t)是位势，而

由相容条件φxt=φtx可得零曲率方程

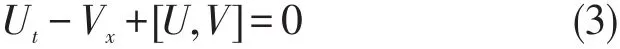
由(3)直接计算，得到如下孤子方程即（1）

为确定谱问题(2)的Darboux变换，我们先引入谱问题(2)的规范变换

这里的T可由下两式确定

从而谱问题(2)转化为

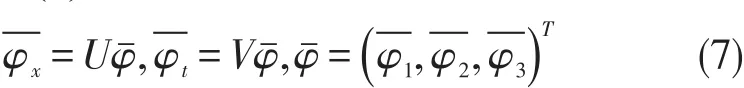
若谱问题的规范变换将谱问题转化为相同形式的谱问题，则谱问题的规范变换称为Darboux变换。由于U,V和具有相同形式，可得T=(tij)3×3的形式为

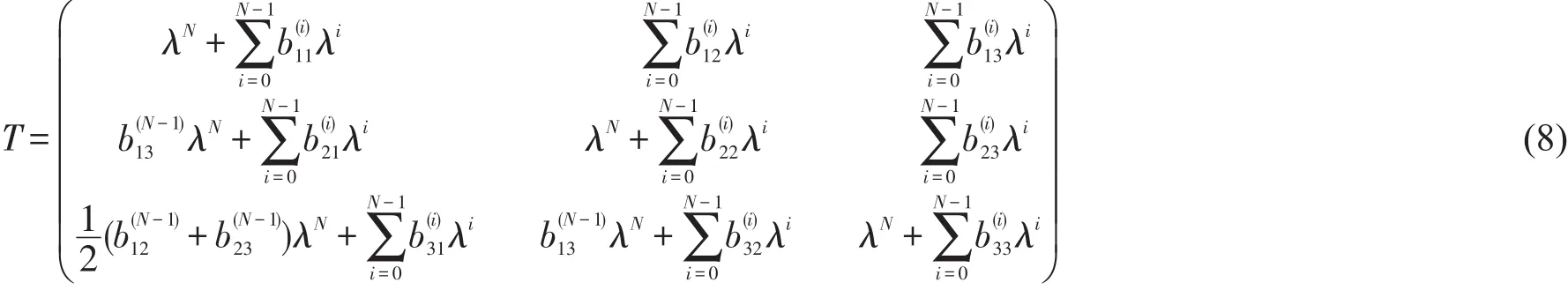
不妨令以下

上式可以写成线性系统

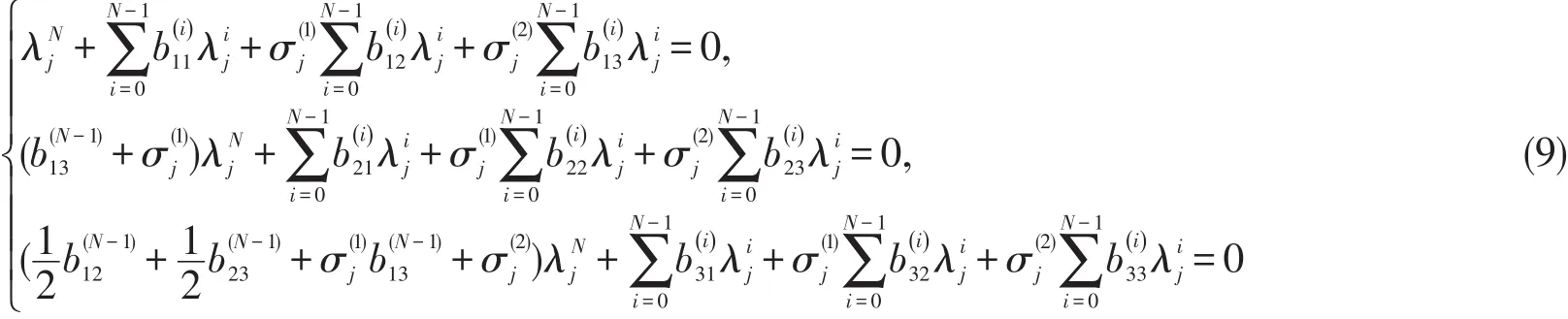
将(8)中的tij(i,j=1,2,3)代入(9)得

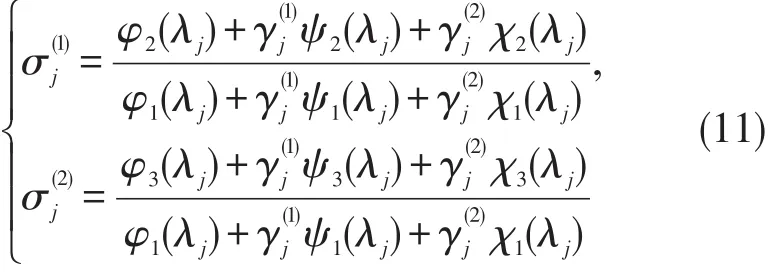
另一方面，由(9)可知

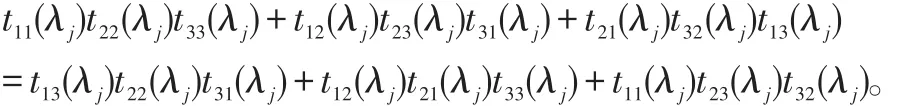
所以

这表明λj(1≤j≤3N)是Det(λ)的根(μ与λ无关)。

命题1由式子确定的矩阵与U具有相同的形式，即可以表示为

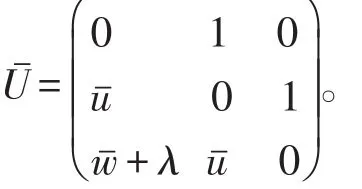
下面变换

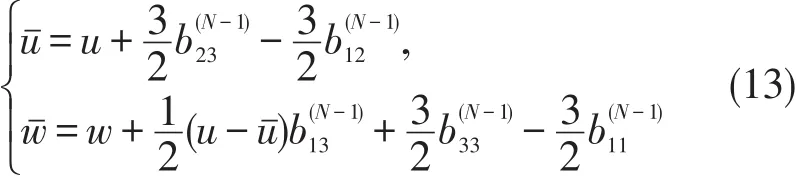
将原位势u,w映射为新位势。

证明设的伴随矩阵）且

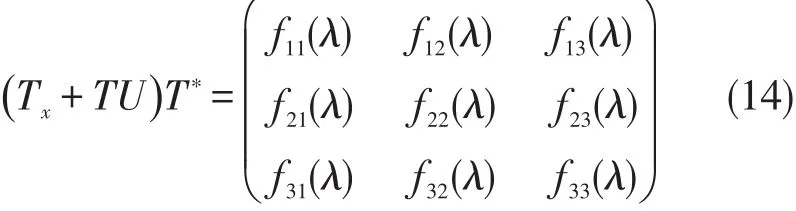
易证fsl(s,l=1,2,3)是关于λ的3N+1次或3N次多项式。当λ=λj(j=1,2,…,3N)时，通过(2)和(9)得出如下关系式

利用(15)可以得到所有的λj(j=1,2,…,3N)都是的根。故(14)能改写为

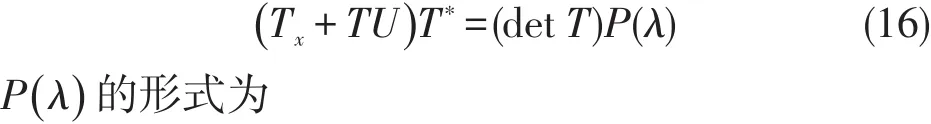
对比上式中的λN+1,λN和λN-1的系数，可以得

注计算式(21),(23)时需用式(26),计算(22)时需用式(25),(28)。对比(5)和(18)，易得

运用命题1的证明方法，同理可以得到。

命题2由式子确定的矩阵与V具有相同的形式，即为

在Darboux变换(4)和(13)作用下，将原位势u,w映射为新位势。其中

由命题1和命题2可知，Darboux变换(4)和(13)将Lax对(2)映射为形式相同的Lax对(7)，且由相容条件可知，两个Lax对都能得到孤子方程(1)。由以上所述可得：

定理1孤子方程(1)在Darboux变换(4)和(13)作用下，将一个解(u,w)映射为另一个解其中包含的由线性系统(9)唯一确定。

2 新精确解

其中，

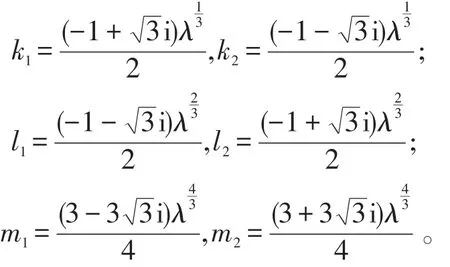
根据线性系统(9)，在简单情况N=1时，利用Cramer法则求得，孤子方程(1)的平凡解为

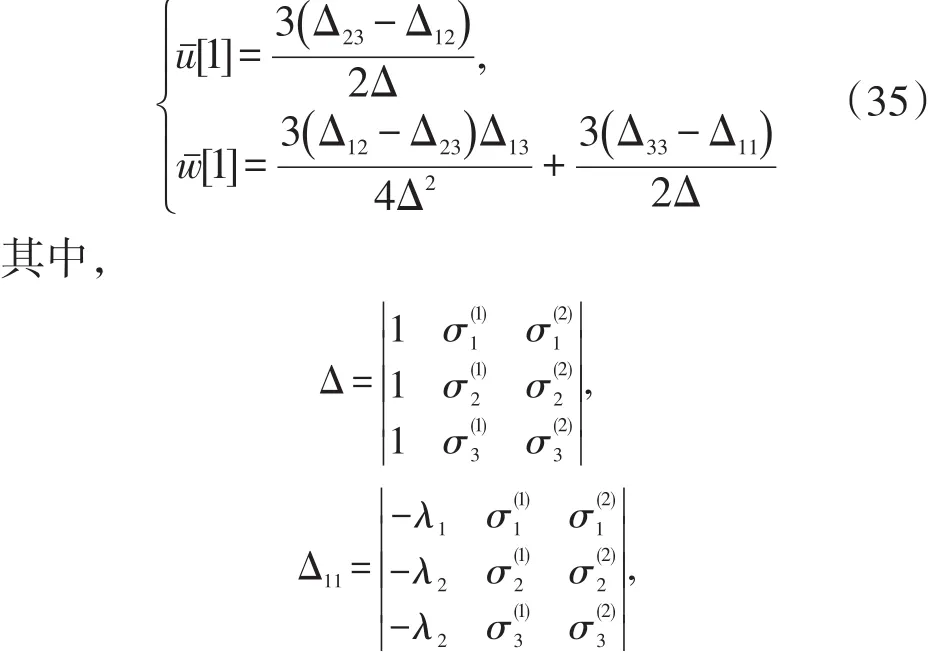
利用上面的Darboux变换可以得到孤子方程(1)的一系列精确解。以它的一平凡解u=w=0作为种子解，代入Lax对(2)中，可以得到(2)的一组基本解。它的三个基本解分别为

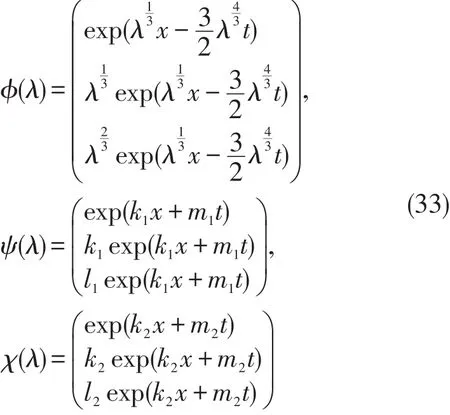
根据式(11)有

选取适当的参数可以得到以下的孤子图解。这里,

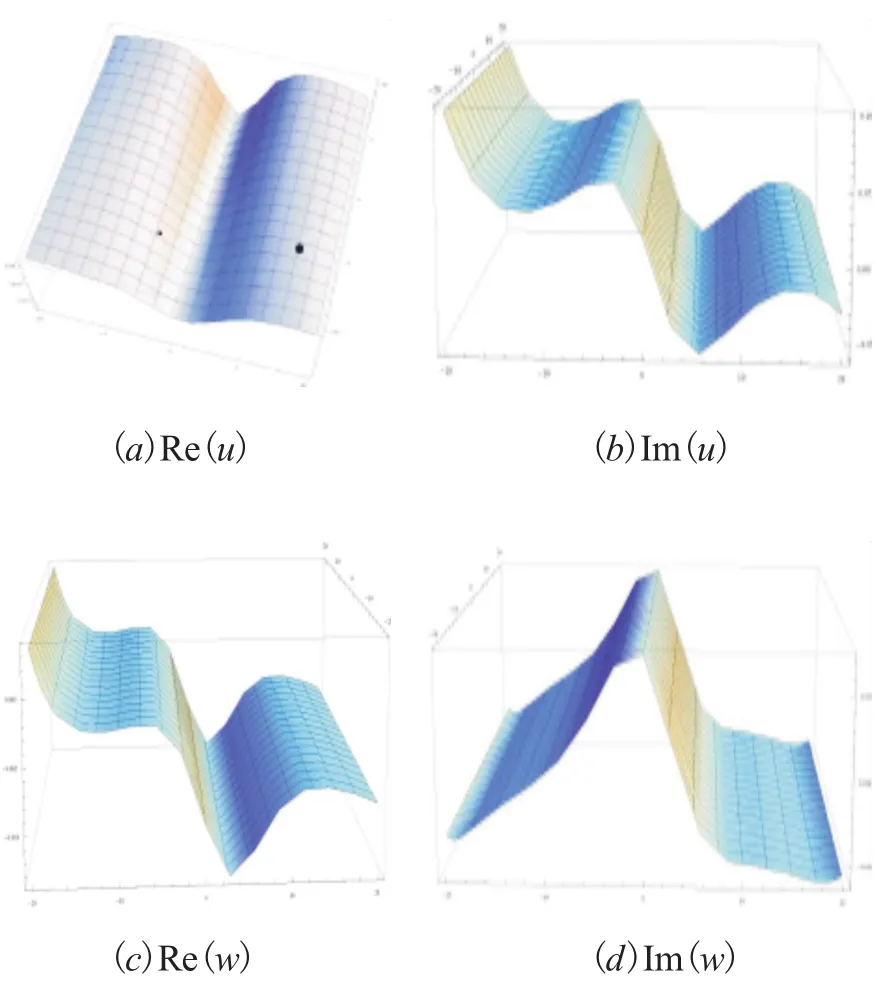
图1 由（35）式决定的孤子解图

通过上述的讨论，我们找出了它的新精确解，也进一步了解了Darboux变换的方法和技巧，同时也使得我们以后可以更好的解决此类问题。

[1]陈登远.孤子引论[M].北京：科学出版社，2008：230-267.

[2]Zhang Y F,Feng B L,Rui W J,et al.Algebro-Geometric solutions with characteristics of a nonlinear partial differential equation with Three-Potential functions[J]. Commun.Theor.Phys.，2015,64(7):81-89.

[3]Li Y S,Zhang J E.Darboux transformations of classical Boussinesq system and its multi-soliton solutions [J].Physics Letters a,2001,284(6):253-258.

[4]耿献国.MKP方程与变换[J].数学年刊，1990，11(3)：265-268.

[5]Wang X,Chen Y.Darboux transformations and n-soliton solutions of two(2+1)-Dimensional nonlinear equations[J].Commun.Theor.Phys.,2014,61(4):423-430.

[6]王振辉，李世金.孤子方程的达布变换及其精确解[J].江汉大学学报(自然科学版)，2014，34(2):34-36.

[7]韩元春.套格图桑.KdV方程的无穷序列新精确解[J].内蒙古师大学报(自然汉文版)，2013,42(5):505-509.

[8]李雪梅，周自刚.四波方程的孤子解[J].郑州大学学报(自然科学版)，2001,33(1):1-3.

[9]黄坤，陈友军.Broer-Kaup系统3类达布变换间的关系及其精确解[J].郑州大学学报(理学版)，2012,44 (3):38-41.

[10]李芳.与高阶谱问题相联系的孤子方程的分解与有限维可积系统[D].郑州：郑州大学，2009.

The Darboux transformation of a soliton equation associated with 3×3matrix spectral problem and its explicit solutions

ZHANG Xin1，LI Xin2
(1.Department of Basic Courses,Hefei Science and Technology College,Hefei Anhui230000,China；2.Experimental training Center,Hefei Normal University,Hefei Anhui230601,China)

The Darboux transformation of a soliton equation with3×3matrix spectral problem was studied.Beginning with the matrix spectral problem which contains two potentials,the Darboux transformation was constructed,and the results were proved completely in terms of the theory.Using this Darboux transformation,the general expression of this hierarchy of nonlinear differential-difference equations can be obtained from a trivial seedu=v=0,obtaining explicit solutions.With the help of Mathematica,some figures are plotted.

soliton equation;Darboux transformation;explicit solutions;spectral problem

O175.3

A

1004-4329（2017）01-008-05

10.14096/j.cnki.cn34-1069/n/1004-4329（2017）01-008-05

2016-11-07

张鑫（1988-），男，硕士，讲师，研究方向：孤立子与可积系统。