基于主成分分析的大学生兼职影响因素探究

潘陈蓉，孙鹏，汪芳凯，陈贝贝，张杰

（阜阳师范学院数学与统计学院，安徽阜阳236037）

基于主成分分析的大学生兼职影响因素探究

潘陈蓉，孙鹏，汪芳凯，陈贝贝，张杰*

（阜阳师范学院数学与统计学院，安徽阜阳236037）

近几年大学生兼职问题受到广泛关注。2015年对安徽省某地方高校在读大学生兼职影响因素进行调研，问卷采用Likert五分量表法，运用主成分分析理论和方差的性质等数理统计知识，对大学生兼职影响因素模型进行研究，得到三个主成分并进一步探究，最后对大学生兼职中存在的问题提出对策建议。

大学生兼职；主成分分析；兼职影响因素

“大学生兼职”意为在校大学生在学习之余从事有报酬的工作活动。考虑到经济发展和社会就业的形势，越来越多大学生选择兼职：既可以获得劳动收入，也是通过实践提升就业竞争力的一种方式。然而，选择兼职时通常存在着一些困惑，比如与所学专业关联度，对学业的冲击，性别因素、兼职中的侵权问题等[1-5]都会影响兼职选择。

主成分分析作为一种经典的综合评价方法，是基于考虑各指标间相互关系，把多个变量问题转换为一个或较少几个彼此独立的典型变量，这些较少的指标在反映原来多个指标的信息时具有代表性，称为主成分，是应用降维思想使问题简单化的多元统计方法。通常主成分分析更适于对模型进行精确的分析[6-7]。在社会与自然科学多要素交互影响的研究中，为了全面客观分析问题，通常要从多方面观察数据。主成分分析可以很好地处理不同角度数据的相关性，实现多指标的综合评价，从而在诸多学科领域有着广泛的应用[8-10]。

本文对安徽省某地方高校在读本科大学生兼职影响因素开展调查，在已有研究和实践基础上建立数学模型，运用主成分分析法得到三个主成分并进一步分析说明，最后为大学生兼职提出积极的建议。

1 模型构建与实证分析

1.1 数据收集

2015年10月，课题组对所在高校影响学生兼职的因素进行摸底[11]，访谈对象为50名在校大学生，涵盖文科、理工科、经管类和艺体类相关专业，主要从大二、大三学生中随机选取。访谈提纲由3个问题构成：(1)是否会选择兼职？（2）选择兼职会关注哪些问题？（3）在校大学生身份对兼职的影响？以这3个问题为主线，适时进行追问，时间控制在20分钟以内，使受访对象在相对轻松的坏境下表明真实想法。课题组由此获得经验数据并对观点归纳，确定大学生兼职的影响因素，进而设计调查问卷细化研究。

考虑到当前大学生兼职主要是机会型而非生存型，调查问卷主要涉及11个兼职影响因素指标，依次为：x1为工作经验，x2为朋友圈，x3为社交能力，x4为实践能力，x5为兼职时间，x6为兼职时段分布，x7为兼职收入，x8为兼职成本，x9为兼职与专业相关度，x10为专业影响力，x11为兼职与学业关系。采用Likert 5分制，1～5分由“非常同意”到“完全不同意”或是“很强”到“没有影响”表明程度。

课题组于2015年12月至2016年3月对省属某地方高校做过兼职的本科学生进行问卷调查，共发放调查问卷360份，回收有效问卷325份，有效回收率达到90%。假设调查得到的数据真实可靠；假设在模型建立过程中使用的数据都是随机选取的。

1.2 模型构建

首先应用主成分分析技术对兼职影响因素指标进行主成分提取。模型主成分的提取就是确定原来变量xj(j=1,2,…,11)在对应主成分zi（i=1,2,…,m)（m≤11)上的载荷lij（i=1,2,…,m；j=1,2,…,11)。

兼职影响因素指标构成一个325×11阶的数据矩阵：

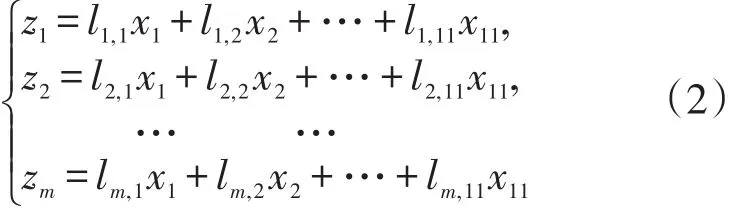
在（2)式中，系数lij由下列条件确定：

相关系数矩阵计算公式为：

R是一个实对称矩阵（rij=rji)，其主对角线上元素全为1，rij（i,j=1,2,…,11)为原变量xi与xj的相关系数：

主成分的贡献率就是主成分解释的方差比例，方差越大，表明这一主成分反映自变量的信息越多。累计贡献率的计算公式为：

主成分载荷矩阵计算公式

其中eki为向量ek的第i个分量。

由此可以进一步计算主成分得分Z[3]为：

1.3 模型分析

首先，选用标准差方法对数据进行标准化处理，用SPSS软件[12]对标准化数据进行KMO检验，得到KMO值为0.750，Bartlett's球形度检验结果中近似卡方值为884.179，sig=0.000，可知适合做主成分分析。

表1 KMO和Bartlett's检验

对标准化处理后的数据进行分析，得到兼职影响因素指标的相关系数矩阵，见表2。

根据相关系数矩阵，计算特征值和各个主成分的方差与累计贡献率，如表3。

由表3可知，第一，第二，第三主成分的特征值大于1且累计贡献率达到58%以上，且其他数据解释量呈明显递减趋势。

同时，由图1可以看出，在第三个成分之后，坡线的走势较为平坦，表示无公因子值得抽取，因而保留三个成分较为合适。记z1为第一主成分，z2为第二主成分，z3为第三主成分。应用最大方差法对成分矩阵进行旋转，使每个变量仅在一个因子上呈现较大的载荷，因子提取方法为主成分分析法，这里提取三个因子。具体数据见表4。

表2 兼职影响因素指标的相关系数矩阵

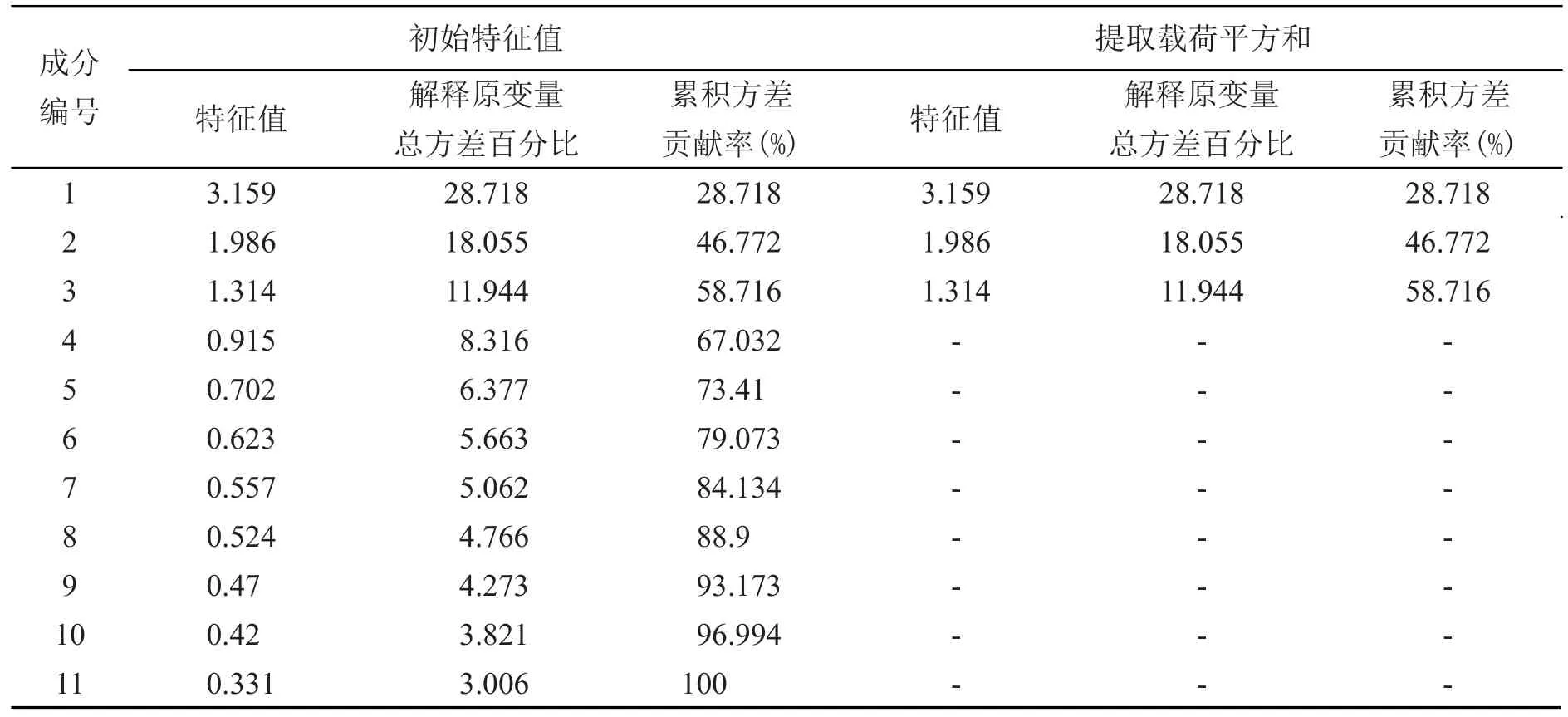
表3 主成分分析的特征值与方差解释量

由表4可以看出，第一主成分在x1、x2、x3、x4这 4项指标上呈现出较大的载荷量，而这4项指标体现了大学生通过兼职所得到的收获，因而命名为兼职收获影响因子。第二主成分由x5、x6、x7、x8这4项指标来体现兼职条件对大学生兼职意愿的影响，命名为兼职条件影响因子。第三主成分包含x9、x10、x11共3项指标，涵盖大学生的专业与学业对兼职的影响，命名为专业学习影响因子。其中，获取工作经验是大学生兼职选择最看重的，社交与实践能力的培养与提高比重也很高，也印证了当前大学生兼职并非传统意识下仅为获取经济收入的生存型。

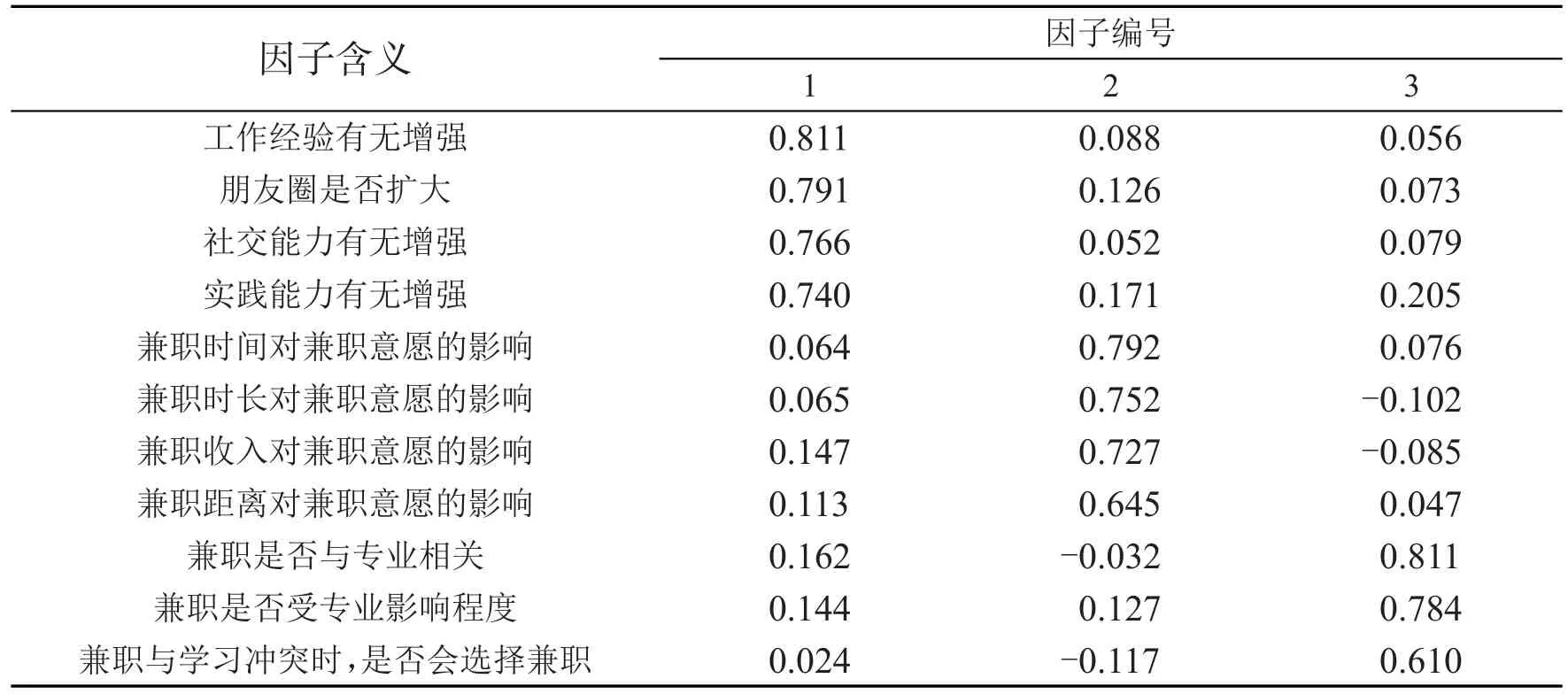
表4 旋转后的因子载荷矩阵

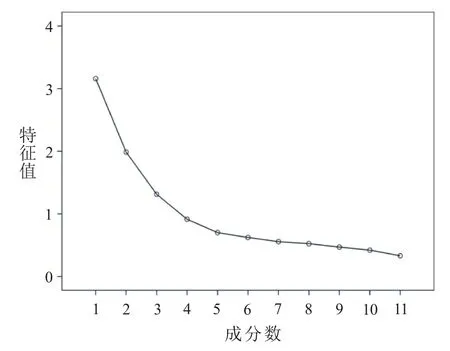
图1 皖北地区大学生兼职影响因素调查问卷的陡坡图

图2 初始因子及旋转后因子载荷分布

将初始载荷矩阵进行旋转后可见主成分更容易识别，图2(a)为初始因子对应于3个主成分的载荷分布图，旋转后的主成分分布如图2(b)。计算各主成分得分如表5所示。

由成分得分系数矩阵可以得出前三个主成分的线性组合表达式为：

表5 成分得分系数矩阵

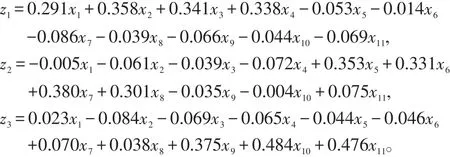
容易看出，第一主成分z1中指标x1,x2,x3,x4比重较大，指标x5,x6,x7,x8在第二主成分z2中比重较大，指标x9,x10,x11对第三主成分有较大影响。

本模型在样本选取方面有一定的局限性，比如选取高校的数量与所在地区、调查对象数等；还有一些影响因素没有体现使得主成分的累计贡献率不高，比如选择兼职对周围同学的辐射影响没有考虑，不同学科专业各年级可以分别展开研究等等。

2 对策与建议

高校应鼓励大学生兼职规划指导的专项研究。比如成立专门的服务机构，发布校内外的兼职岗位，使信息发布有专业化导向并使兼职有安全保障。开展就业指导课程的教学，普及职业发展和就业基础知识；建立并开放大学生职业规划工作室，开展个性化职业指导等。

学校对大学生兼职还应给予必要的理论引导。选择兼职不应局限于改善经济状况，更要考虑立足于自我发展。同时可以通过参加大学生创新创业项目、职业规划设计比赛、顶岗实习等锻炼方式提升自我就业竞争力。

需要注意的是，大学生在兼职中时有侵权现象发生，要树立和增强安全意识、维权意识，懂得自我保护。

[1]李林原，蒋佳芮，张静，等.层次分析法在大学生兼职规划中的研究[J].成都师范学院学报，2016,32(3): 119-124．

[2]颜艳.基于成本收益理论的大学生兼职分析[J].教育教学论坛，2015,44:57-59.

[3]徐悦，王军，郭宏.大学生兼职情况调查与对策研究[J].安徽工业大学学报(社会科学版),2015,32 (2):117-119.

[4]赵果.大学生兼职的现状调查与职业发展研究[J].辽宁师范大学学报(社会科学版)，2013,36(6):859-863.

[5]涂婷，黄文龙，华珊，等.在校女大学生兼职情况的调研报告[J].湖北经济学院学报(人文社会科学版)，2010,7(9):154-156.

[6]方开泰.实用多元统计分析[M].上海：华东师范大学出版社，1986：339-352.

[7]邓雪，江璐瑶，孙全德.多元统计分析方法的理论研究及应用分析[J].数学的实践与认识，2016,46(4): 190-197.

[8]马志飞，李在军，张雅倩.基于地理加权主成分的经济发展综合评价研究[J].华中师范大学学报:自然科学版，2016,50(2):276-281.

[9]刘二林，俞葵.基于主成分分析的安徽省区域产业结构优化效率评价[J].安徽工程大学学报，2014,29 (4):69-74.

[10]石洪景，黄和亮.基于主成分分析的食品价格影响因素研究[J].北京航空航天大学学报(社会科学版)，2012,25(5):77-80.

[11]刘星，李新建.基于扎根理论的多元雇佣工作群体的雇佣身份断层与激活因素研究[J].管理学报，2015,12(7):1001-1011.

[12]王苏斌，郑海涛，邵谦谦，等.SPPS统计分析[M].北京：机械工业出版社,2003:43-48.

Study on the influence factors of college students’part-time job based on principal component analysis

PAN Chen-rong，SUN Peng，WANG Fang-kai，CHEN Bei-bei，ZHANG Jie*
(School of Mathematics and Statistics,Fuyang Normal University,Fuyang Anhui236037,China)

The issue of college students'part-time job has attracted much attention recently.Applying Likert scale method to investigate the students'part-time job in a certain college of Anhui province in 2015,using principal component analysis and variance's properties in mathematical statistics,the problem of part-time job was studied,and three principal components are extracted for a further study.Finally,some countermeasures and suggestions are put forward for the problems appeared in the college students'part-time job.

college students'part-time job;principal component analysis;influence factors of part-time job

O212.4,G646

A

1004-4329（2017）01-021-05

10.14096/j.cnki.cn34-1069/n/1004-4329（2017）01-021-05

2016-08-20

安徽省大学生创新创业训练项目（201510371071）；阜阳师范学院教学团队（2014JXTD01）资助。

张杰（1981-)，女，硕士，讲师，研究方向：概率统计。Email：zjp562@126.com。