GM—AR模型在城市地面沉降预测中的应用

张玲霞 赵晓光 曹庆东

【摘要】随着城市的现代化进程，地面沉降已广泛发生在世界各地，给人民生活和社会发展造成极大损失。GM（1，1）模型作为经典的地面沉降预测方法得到了广泛应用，不适用于随机型数据预测。将AR模型与GM（1，1）组合成GM-AR模型对城市地面沉降数据进行预测，预测值残差小于GM（1，1）模型，未来2、3期预测值小于1mm，且趋势线更贴近实测值，效果优于传统的GM（1，1）模型。

【关键词】灰色模型；自回归模型；城市地面沉降

Application of GM - AR Model in Urban Ground Subsidence Prediction

Zhang Ling-xia1，Zhao Xiao-guang2，Cao Qing-dong1

（1.Shandong Yellow River Survey and Design InstituteJinanShandong250000；

2.Shandong Yellow River Information CenterJinanShandong250000）

【Abstract】With the modernization of the city， land subsidence has been widespread in the world， to the people's lives and social development caused great losses. GM （1，1） model has been widely used as a classical ground subsidence prediction method， and it is not suitable for stochastic data prediction. The AR model and GM （1，1） are combined into the GM-AR model to predict the urban ground subsidence data. The predicted residual value is less than GM （1，1） model， the predicted value of the next two is less than 1mm， and the trend line More close to the measured value， the effect is better than the traditional GM （1，1） model.

【Key words】Gray model；Autoregressive model；Urban land subsidence

1. 引言

（1）地面沉降是在自然和人為因素作用下，由于地表松散土体压缩而导致区域性地面标高降低的一种环境地质现象[1]，人类的生存活动如地下水资源、矿产资源的开采，高层建筑物的建造等，都会破坏原有的土层结构，打破地壳上部的受力平衡，使地表塌陷或凸起造成土壤变形。随着工业的发展和人口的增长，工业用水及居民生活用水量大大增加，资源的消耗量持续上升，高层建筑群的数量也逐年增加，致地面沉降广泛发生于世界各地，给人民生活和社会发展造成极大损失，今年来随着城市建设的逐步开展，随之也给地质带来了影响，为了保证城市建设的顺利进行，有必要对城市地面的变化进行监测和未来变化进行预测。

（2）采用数学模型进行逼近、模拟、揭示变形特性从而进行地面沉降预测成为近年来研究的热点，常用的数学预测模型有GM（1，1）模型（灰色模型）、Kalman滤波、人工神经网络模型、时间序列分析等预测模型，以上模型具有自己的使用条件和优缺点，采用不同的预测模型可以得到不同的预测结果。在数学预测模型中GM（1，1）模型（灰色模型）适用于分析具有确定性趋势的数据[2]，现已被广泛应用[3]；AR模型（Auto Regressive，自回归模型）采用的是随机过程中自身历史值的线性组合来描述整个过程[4]，该方法能够适用于分析平稳的随机监测数据[2]，但是由于城市地面沉降受到多种因素的影响，但大致可分为确定性部分和随机性部分，因此，本文将采用两种模型进行组合的方式GM-AR组合模型对城市地面沉降数据进行分析预测，并与只采用GM（1，1）模型（灰色模型）的预测结果对比，分析GM-AR组合模型的应用效果。

2. AR模型原理

AR模型设时间序列观测值为为y0，y1 ，…yn ，模型为P阶，序列中其余元素与前 P个元素可组成关系[5][6]如式（1）

y ^ p+1=yp1 +yp-12+…+y1p+Δp+1

y ^ p+2=yp+11 +yp2+…+y2p+Δp+2

……

y ^ n=yn-11 +yn-22+…+yn-pp+Δn

（1）

式中， y ^ i 为预报值，1，2，…，p 为参数， Δi为观测误差，共有 n-p个方程

则AR（P） 模型的预报方程为式（2）

y ^ =∑n i=P+1 yi ^ i-p （2）

3. GM-AR组合模型

3.1灰色模型GM（m，n）的基础概念是灰色模块，核心模拟建模方法是微分拟合法，其中模型参数m是模型微分方程的阶数，n是参与建模的序列个数，在建模时微分方程阶数越大，计算就复杂，但是精度的提高则不明显，因此本文中就采用m=1，n=1时的模型GM（1，1）作为预测模型，令非等间隔时间序列观测值x0， x1，…，xn，然后通过内插得到等间隔时间序列建立GM（1，1）模型，建立过程如下：

3.2对 x0（t）进行1次累加得到递增序列 x1（t）=x1（1），x1（2），…，x1（n）通过1阶灰色模块构成一阶线性微分方程 dx（1）dt+ax1=b，其中a是用以控制系统发展态势的大小称之为发展系数，b用来反应资料数据之间变化的关系，称之为灰色作用量；通过原始数据序列构成大于2的方程组，令Y=XB+E其中E为误差项，Y，B为：endprint

Y= x0（2） x0（3） x0（n） ，B= ab （3）

3.3根据最小二乘原理得到最小二乘解：B=（XTX） -1（XTY） =[ab]T，把a，b值带回原方程得

x（1）t= x0（t）-ba e-at + ba （4）

3.4求出其残差序列y0， y1，…，yn， 对残差序列建立AR模型，则利用GM-AR组合模型对沉降量的预测结果可写为： x（t） = x0（t）-ba e-at + ba

+∑yi ^ i-p

（5）

式中，前一项为GM（1，1）模型部分，后一项为AR（p）模型部分。

4. 实例分析

4.1采用某地二等水准测量沉降观测数据，应用GM（1，1）模型与GM-AR模型对比分析，取AR模型阶数P=4 ，预测结果及残差见表1。

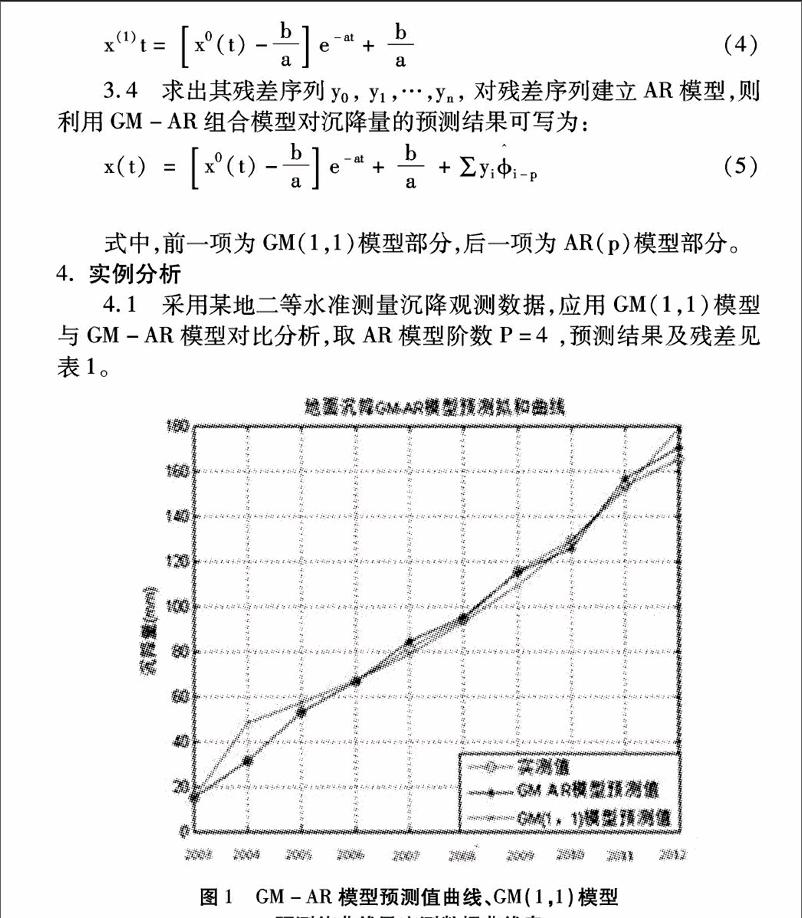
4.2为方便直观的表现模型效果，現将实验中的GM-AR模型预测值曲线、GM（1，1）模型预测值曲线及实测数据绘制成图，效果如图1所示：

4.3由表1可以看出，GM（1，1）模型虽能对沉降量做出预测，但残差很大，在预测第3期数据时残差绝对值已出现大于5mm的情况，在预测第6期数据时残差绝对值已大于10mm；GM-AR模型，预测值残差较小，在预测第6期数据时残差绝对值等于5mm，前5期均小于5mm，未来第2、3期数据的预测值残差绝对值在1mm之内。由图1可知，GM-AR模型预测值曲线、GM（1，1）模型预测值曲线及实测数据走势大致相同，但GM-AR模型预测值曲线走势更接近于实测数据，从图像未来发展趋势看，GM（1，1）模型曲线在未来第6期数据以后已偏离了实测数据，而GM-AR模型预测值曲线依然与实测数据走势相同，且更接近于实测数据。

5. 结论与展望

（1）GM（1，1）模型、GM-AR模型都是预测地面沉降的有效方法。GM（1，1）模型对确定性趋势的数据预测效果较好，AR模型适合分析随机性数据。本文将上述两种模型结合，在使用GM（1，1）模型对地面沉降观测值的确定性部分预测后，使用AR模型对其预测残差再进行拟合，补充GM（1，1）模型对于沉降数据随机性部分预测的缺失，从而达到对地面沉降的精确预测，且GM-AR模型形式简单、参数较少，满足城市地面沉降等相关工程的建模、预报需求。

（2）随着城市的发展，对于城市地面沉陷理论的研究也在逐步深入，预测模型之间的组合预测验证也将会得到进一步的研究，同事模型预测的精度需要大量数据的验证，所以未来对于沉陷数据的采集将会更加智能化和集中化，高效便捷的采集数据手段都已出现如三维扫描技术等。

参考文献

[1]郑铣鑫，沿海地区城市发展与地面沉降的系统控制[J]，海洋地质与第四纪地质，1992，（1）：57～65.

[2]高宁，崔希民，高彩云.灰时序GM-AR模型在建筑物沉降变形预测中的应用[J].测绘科学，2013，38（1）：139～141.

[3]王有良，唐跃刚.曲线拟合与GM（1，1）模型沉降预测及相关性分析[J].测绘科学，2008，（3）：98～99，78.

[4]金瑶，蔡之华.基于AR模型的Kalman滤波在股票价格预测中的应用[J].统计与决策，2013，（6）：80～82.

[5]焉建国， 陈正松， 罗志才， 等. 基于 AR 模型的上海地区地面沉降预测分析[J]. 大地测量与地球动力学， 2009， 28（5）： 121～124.

[6]兰孝奇，杨永平，黄庆，严红萍.建筑物沉降的时间序列分析与预报[J].河海大学学报（自然科学版），2006，34（4）：426～429.

[7]曾山，徐兮.基于AR模型的填方路基沉降检评方法[J].重庆交通大学学报（自然科学版），2013.endprint