涡激振动能量收集的理论建模与实验验证
2017-09-25杨敬东刘永臻张鸿鑫
杨敬东,刘永臻,张 敏,张鸿鑫
(重庆交通大学 航运与船舶工程学院,重庆 400074)
涡激振动能量收集的理论建模与实验验证
杨敬东,刘永臻,张 敏,张鸿鑫
(重庆交通大学 航运与船舶工程学院,重庆 400074)
为了研究涡激振动压电能量收集特性,根据压电理论和尾流振子模型建立二维涡激振动的压电能量收集数学模型,对一个圆柱加双压电臂的能量收集装置进行计算分析。结果表明:输出电压随着负载电阻的增大而增大,最大输出功率存在一个最佳匹配电阻。之后开展压电能量收集风洞实验,理论分析结果与实验结果吻合,验证了理论模型的正确性。该模型对进一步设计和优化涡激振动能量收集装置有参考价值。
机电工程;能量收集;尾流振子模型;VIV;圆柱
0 引 言
压电能量收集在近几十年中一直是能量收集研究领域关注的焦点,其原理是将周围结构的振动转换成电能[1]。从近几年学者们有关压电收集的综述来看,基于振动能量的压电发电的装置[2]的研究较多,因此出现了各种各样的压电发电装置。压电装置应用广泛,不仅用于传感器[3],也应用于能量收集。由于国内外对涡激振动(VIV)发电的应用尚处于理论和实验室阶段,其结构形式、性能特点、应用范围等都亟待进一步深入研究,因此该方面的研究相对较少。
涡激振动是在一定速度的流体流经钝体时,会在结构的尾迹中旋涡以一定频率交替脱落,产生周期振荡的升力,导致结构以一定的频率和振幅振动[4]。在一定流速下,旋涡脱落频率接近结构固有频率时,结构会发生共振,涡激振动的基本特点有锁定现象和滞回现象[5]。涡激振动具有非线性,因此可以采用尾流振子模型把结构近壁的尾涡动力特性通过非线性振子来模拟,例如采用Van der Pol方程或者Rayleigh方程来描述其自激自限的谐振动过程,并与结构振子联立构成方程组,共同预测流固耦合系统的响应[6]。
涡激振动能量收集应用潜力巨大,但是其中关键技术并不成熟。对于该问题,近年来学者们做了有意义的研究。如M.M.BERNITSAS等[7]提出了一种基于涡激振动的清洁水能源收集系统;WU Nan等[8]研究仿真了压电片的长度以及安装位置在涡激振动中的压电能量收集的影响;A.PERELLI等[9]利用压电技术以及涡激振动理论提出了用于水下能量收集的压电发电机设计和性能分析;张敏[10]等人对涡激振动压电能量收集进行了数值分析。
基于涡激振动能量收集的相关研究结果,笔者建立了双压电悬臂梁连接圆柱的涡激振动能量收集模型,进行流体激励振动的能量收集理论分析,研究不同负载电阻的输出电压以及功率特性。之后进行了能量收集实验,对理论分析结果与实验结果惊醒了对比,验证理论模型的正确性。
1 压电能量收集模型
图1为压电能量收集装置,两个双晶压电臂安装在圆柱的横向振动方向用以收集能量。图1中:U为风速、Rl为电阻、C为阻尼、K为弹簧刚度、Y(t)为圆柱横向位移。

图1 压电能量收集装置示意Fig.1 Schematic of a piezoelectric energy harvester
为便于研究,将压电能量收集系统等效为单自由度的弹簧-质量-阻尼系统[11],则系统控制方程为弹性支撑的刚性圆柱振动与高斯公式的耦合方程[12],如式(1)、(2):
(1)
(2)
式中:M为振动质量;ξ为阻尼比;ωn为结构固有频率;F(t)为流体力;θ为机电耦合系数;V为负载上的电压;R为负载电阻;Ce为压电等效电容。
M.L.FACCHINETTI等[13]所建立的尾流振子模型如式(3)、(4):
(3)

(4)
式中:mf=1/4πCmρD2为附加质量;Cm为附加质量系数,当钝体为圆柱时,Cm=1;cf=ΩfγρD2为附加阻尼,γ=CD/4πSt=0.8;q(t)=2CL(t)/CL0,CL0=0.3;Ωf=2πUSt/D为涡脱频率,St=0.21,CD=2;ε和A为经验参数,ε=0.3,A=12。
应用尾流振子模型将式(1)可改写为式(5):

(5)
式(2)、(3)、(5)即为基于尾流振子模型的涡激振动压电能量收集装置的数学模型。
系统的结构、电路连接与等效电路如图2。双晶压电臂采用串联方式,两个压电臂使用导线采用并联方式连接至负载电阻R。

图2 系统结构和电路示意Fig.2 Schematic of system structure and circuit
压电等效电容Ce及机电耦合系数θ可用式(6)和(7)表示[14]:

(6)
θ=e31(hp+hs)b
(7)
式中:Cp为单压电层的电容;e31为压电常数;ε0为真空介电常数(相对介电常数);L、b、hp分别为压电层的长、宽、高;hs为基层高度。
2 理论计算
装置具体参数见表1和表2。压电材料选用PZT-5H,基层材料为铜。通过改变风速和电阻值获得不同情况下负载上输出电压的值,从而得到不同负载电阻输出电压随风速的变化曲线,如图3。

表1 压电装置结构参数

表2 压电振子材料属性
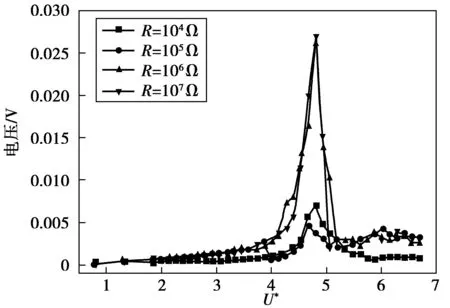
图3 不同电阻时输出电压VIV响应曲线Fig.3 VIV response curves of output voltage with different resistances
由图3可知,当在共振频率值附近时,振动达到最大值,且随着电阻的增大,电压随之增大。当电阻值介于104~105Ω时,电压的绝对值较低,增大的幅度较小;当电阻值达到106Ω时,电压有一个明显的升高,当电阻值介于106~107Ω时,电压仍然增大,但增大的幅度也变小。其最大电压随电阻变化的趋势如图4。

图4 最大电压随电阻变化的趋势Fig.4 The trend of the maximum voltage changing with resistance
由图3中来流速度与输出电压之间的关系曲线可知,各电阻的最大电压出现在U*=4.81时。其中风速可调范围为0.82≤U*≤7.03,U*为折合速度,其表达式为:U*=2πU/ωnd。
3 实验研究
实验选用一个直径d=10 mm的圆柱,压电材料选用PZT-5H,压电基层为铜,压电装置各参数与表1一致。实验在亚音速开路风洞中进行,空气由一组1.5 kW的电机带动离心风机驱动,测试段剖面为300 mm2×300 mm2,长度为2 000 mm;压电装置的两个压电臂垂直夹持在测试段的中部,用以进行VIV实验;负载电阻的输出电压使用TEK2002B示波器进行记录,主要实验装置及安装情况如图5。

图5 压电能量收集实验装置Fig. 5 Experiment device of piezoelectric energy harvesting
VIV实验选用4个电阻值作为负载,分别为104、105、106、107Ω,在同一风速下更换不同阻值的负载,示波器并联在负载上进行数据采集,通过逐步增大风速进行实验,并记录电压的输出情况。实验的风速可调范围控制在0.82≤U*≤7.03。将采集到的数据进行整理分析,绘制其不同电阻时输出电压及输出功率VIV响应曲线如图6。
由图6(a)可知,实验中各电阻出现最大输出电压的位置大部分都在U*=4.91附近,表明此时系统处于锁定状态,振动达到最大值。随着电阻的增大,电压随之增大。当电阻值介于104~105Ω时,电压的绝对值较低,增大的幅度较小;当电阻值达到106Ω时,电压有一个明显的升高,当电阻值介于106~107Ω时,电压仍然增大,但增大幅度也变小。
由图6(b)可知,各电阻的最大功率也出现在U*=4.91处,系统的最大功率出现在电阻值为106Ω时。通过实验可知,能量收集系统存在一个最佳的电阻值使得系统的输出功率最优。
将实验得到的结果与理论计算结果相比较,如图7。由图7可看出:实验结果与理论结果的量级以及总体变化趋势一致。

图7 理论计算与实验输出电压对比Fig.7 Comparison of theoretic calculation and experimental output voltage
4 结 语
笔者建立了基于涡激振动的能量收集模型并进行了理论计算分析,得到不同阻值时最大值出现在U*=4.81位置与实验结果U*=4.91非常接近,证明理论模型是正确的。
理论计算及实验结果均表明:输出电压随着负载电阻的增大而增大,输出功率存在一个最佳电阻值,当阻值超过这个最佳值后电压会相应的增大,而功率会随着降低。下一步,将该模型用于能量收集装置的设计及优化过程中,进一步提高该装置的能量转换效率和输出功率。
[1] MICHELIN S,DOARÉO.Energy harvesting efficiency of piezoelectric flags in axial flows[J].JournalofFluidMechanics, 2012, 714(1):489-504.
[2] 陆兆峰,曹源文,秦旻.压电式加速度计在工程测振中的应用分析[J].重庆交通大学学报(自然科学版),2008,27(4):643-646. LU Zhaofeng, CAO Yuanwen, Qin Min. Analysis and application of piezoelectric accelermeter on vibration measurement[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2008, 27(4): 643- 646.
[3] MARQUI C D, ERTURK A, INMAN D J. Piezoaeroelastic modeling and analysis of a generator wing with continuous and segmented electrodes[J].JournalofIntelligentMaterialSystems&Structures, 2010, 21(21):983-993.
[4] ROUNDY S, WRIGHT P K, RABAEY J M.EnergyScavengingforWirelessSensorNetworks:WithSpecialFocusonVibrations[M]. Amsterdam: Kluwer Academic Publishers, 2004.
[5] 秦伟.涡激振动的非线性振子模型研究[D].哈尔滨:哈尔滨工程大学,2011. QIN Wei.TheStudyofNon-linearCouplingModelinVortex-InducedVibration[D]. Harbin: Harbin Engineering University, 2011.
[6] 秦伟,康庄,宋儒鑫.基于离散点涡的双自由度涡激振动尾流振子模型研究[J].工程力学,2012,29(9):294-299. QIN Wei, KANG Zhuang, SONG Ruxin. Research on wake-oscillator model in 2-DOF vortex-induced vibration of cylinder based on discrete point vortex[J].EngineeringMechanics, 2012, 29(9): 294-299.
[7] BERNITSAS M M, RAGHAVAN K, BEN-SIMON Y, et al. VIVACE(vortex induced vibration aquatic clean energy): a new concept in generation of clean and renewable energy from fluid flow[J].JournalofOffshoreMechanics&ArcticEngineering, 2006, 130(4):619-637.
[8] WU Nan, WANG Quan, XIE Xiangdong. Wind energy harvesting with a piezoelectric harvester[J].SmartMaterials&Structures, 2013, 22(9): 23-31.
[9] PERELLI A, FAGGIONI O, SOLDANI M, et al. Design and performance analysis of a piezoelectric generator by Von Karman vortexes for underwater energy harvesting[J].JournalofEnergyChallengesandMechanics, 2014, 1(3): 127-132.
[10] 张敏,谢玉林,雷林,等.基于XFlow的涡激振动压电能量收集数值研究[J].重庆交通大学学报(自然科学版),2017,36(1):103-109. ZHANG Min, XIE Yulin, LEI Lin, et al. Numerical research of piezoeletric energy harvesting from VIV based on Xflow[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2017, 36(1): 103-109.
[11] NOЁL E D, BRIAN L W, SANG-GOOK K. Design considerations for mems-scale piezoelectric mechanical vibration energy harvesters[J].IntegratedFerroelectrics, 2005, 71(1): 121-160.
[12] ZHANG Min, LIU Yingzheng, CAO Zhaomin. Modeling of piezoelectric energy harvesting from freely oscillating cylinders in water flow[J].MathematicalProblemsinEngineering, 2014, 2014: 360-373.
[13] FACCHINETTI M L, LANGRE E D, BIOLLEY F. Coupling of structure and wake oscillators in vortex-induced vibrations[J].JournalofFluids&Structures, 2004, 19(2):123-140.
[14] LONGINI I M J, ACKERMAN E, KEMPER J. An experimentally validated bimorph cantilever model for piezoelectric energy arvesting from base excitations[J].SmartMaterials&Structures, 2009, 18(2):9-18.
(责任编辑:刘韬)
ModelingofVortex-InducedVibrations(VIV)EnergyHarvestingandExperimentalValidation
YANG Jingdong, LIU Yongzhen, ZHANG Min, ZHANG Hongxin
(School of Shipping & Marine Engineering, Chongqing Jiaotong University, Chongqing 400074, P.R.China)
In order to study vortex-induced vibration of piezoelectric energy harvesting characteristics, a two-dimensional mathematical model about piezoelectric energy harvesting was established based on the theory of piezoelectric and wake oscillator model. An energy harvesting device of a cylinder with double piezoelectric cantilever beam was calculated and analyzed. The results show that the output voltage increases with the increase of load resistance. The maximum output power has an optimum matching resistance. Then the wind tunnel experiment of piezoelectric energy harvesting was conducted. It is demonstrated that the experimental results are consistent with the calculation results and the correctness of the proposed theoretical model is verified. The proposed model provides reference to further design and optimization of vortex-induced vibration energy harvesting system.
electromechanical engineering; energy harvesting; wake oscillator model; vortex-induced vibration; cylinder
U664.1;TN384
:A
:1674-0696(2017)09-104-04
10.3969/j.issn.1674-0696.2017.09.19
2016-07-15;
:2016-11-08
福建省科技厅重点资助项目(2014H0010)
杨敬东(1970—),男,重庆人,高级工程师,主要从事现代造船技术与新能源开发方面的研究。E-mail:274245970@qq.com。
