基于公交动态网络的发车频率优化研究

张卫华，吴镇宇，柏海舰，王胜萍

(合肥工业大学 汽车与交通工程学院，安徽 合肥 230009)

基于公交动态网络的发车频率优化研究

张卫华，吴镇宇，柏海舰，王胜萍

(合肥工业大学 汽车与交通工程学院，安徽 合肥 230009)

以公交站点作为动态网络的节点，融合车辆分布与站点乘客需求对公交网络服务均衡性的影响，构建以站点乘客总等车时间为边权的公交动态网络模型，确立公交网络服务与公交动态网络结构的对应关系。在此基础上，以动态网络的时空均衡性为目标，构建网络的状态识别机制，并分析了客流高峰、平峰条件下，公交动态网络在时空上的变化规律。最后，以优化动态网络的时空均衡性为目标，建立普通线路发车频率优化模型。通过实例计算发现，该模型可以获取稳态网络目标下普通线路的最优发车频率，为公交车辆调度的相关问题研究提供一种新的思路。

交通工程；公交客流；公交动态网络；公交调度；发车频率

作为由拓扑网络子系统和流量子系统共同构成的复杂、动态的巨系统[1]，公交系统不仅具备网络的基本属性，还有客流加载的加权网络特性。复杂网络理论的发展为公交系统研究提供了全新的理论方法，由此可将其抽象为由公交线路和停靠站点构成的复杂网络。现有对城市公交行为的特征分析，多集中于研究公交网络静态拓扑结构，主要有L空间方法、P空间方法和公交线路空间处理3种方法[2]。高自友等[3]从城市交通系统的角度出发，探索了城市交通网络的时空复杂性，并对其演化机理进行研究分析；袁春岭[4]和王锟[5]在复杂网络理论的研究基础上，从公交动态网络角度出发，结合不同建模机制，对公交动态加权网络拓扑结构特性进行分析。

目前公交建模研究多集中于静态建模机制[6]，短期内网络的拓扑结构稳定性强，但当线路面临调整，如线路的走向发生变化、节点失效，节点关联性的失效会对网络的拓扑结构产生影响。考虑到传统的公交静态线网实时性较差，给公交调度策略的制定带来一定的困难，因此在公交调度研究领域中引入公交动态网络理论，可通过车辆在网络上的实时分布位置，进而形成一种新的网络评价方法。

1 面向客流需求的公交动态网络

1.1 建模思路

笔者构建的面向客流需求的公交动态网络模型是以各个公交站点来构成城市公交系统网络的节点集合，且节点间相互连接关系则由公交线路客流及公交车辆在网络中的具体运营位置共同确定。模型旨在对公交站点间的服务机会进行研究，也即是分析在公交运营方向上是否存在服务站点i、j的车辆，且其到达站点时间在乘客候车的上下限时间之间。模型以公交网络中站点间的连接关系为权重系数，以乘客总候车时间为权值，若两站点间不存在连接关系，则权重为0[7]。随着时间、地点以及网络环境的不断变化，网络拓扑结构也发生改变。以这种方式构建的公交网络具有时空动态复杂性，是一个逐渐演化的过程。

1.2 网络拓扑结构

在对城市公交网络模型的复杂性进行研究分析时，以邻接矩阵O表示网络中节点间的连接关系，通过建立加权公交复杂网络邻接矩阵O=(oij)对公交网络的结构进行研究；其中：i、j=1,2,…,N。N为站点总数，N个节点构成的邻接矩阵是一个N阶方阵；oij表示节点i、j之间的连接权重(其值为任意非负数)，它不仅表现两节点间是否存在连边，还表明节点间连接强度，oij越大节点联系越密切，反之越疏远。网络中任意节点的点权值可表示为该节点与所有相邻节点的边权值之和，点权值越大的节点在公交网络中地位越重要，则此类公交停靠站点可定义为关键节点。

tv=ta+tcro+tst

(1)

该模型中，乘客只选择出行时间最短的公交线路。考虑换乘客流时，整个公交网络的客流矩阵FC可当作由直达客流矩阵FZ和换乘客流矩阵FT叠加共同组成的，且换乘客流可表示为由若干条换乘线路的子直达客流，如式(2)：

FC=FZ+FT

FT=FT1+FT2+…+FTn

(2)

式中：FTn为换乘乘客在第n条线路直达量。

笔者以一条实际公交线路举例，分析邻接矩阵及拓扑结构的构建。给定任一公交线路，假定其发车间隔为6 min，该线路站点设置和车辆运行时刻分布状态如图1，从左至右依次对站点和公交车辆进行标号，站点编号为1-7，车辆编号为A-F。

给定每个公交站点的客流OD量以及某个时刻各站点的车辆最短到站时间Ti如下，其中假设服务于第i站点到其余站点车辆与其余站点车辆到达第i个站点的时间是相同的。

图1 公交站点设置及车辆运行状态分布Fig. 1 Setting of bus station and distribution of vehicle running state

(3)

其中：乘客可接受的等车时间默认为10 min，车辆在站点的服务时间默认为1 min。假定站点1为公交线路的始发站，默认此处乘客的最短候车时间为车辆的发车间隔。当车辆D到达站点5时，其车辆最短等车时间为站点的服务时间。

根据上述规则，网络节点的邻接矩阵如式(4)：

(4)

根据邻接矩阵构建网络的拓扑结构，如图2。

图2 基于邻接矩阵的城市公交网络拓扑结构Fig.2 Topology diagram of urban public transport networkbased on adjacency matrix

2 公交动态网络状态的均衡性分析

2.1 不均衡性指标的定义

研究客流分布状态与公交车辆运行之间的内在规律，即是研究网络中车辆的分布状态与站点客流需求是否相匹配。在公交动态复杂网络当中，各节点强度的差异性越大，车辆分布与客流需求之间的匹配性越差。假定在一定发车间隔内，客流与车辆分布的不均衡性指标P用式(5)表示：

(5)

不均衡性指标P表示网络中各节点强度与网络平均节点强度的差异情况。在公交系统运力一定的前提下，P值越小表明各节点强度的差异性越小；而当P趋向于0时，各节点强度几乎无差异，此时公交车辆处于最优的分布状态。

2.2 不均衡性指标的计算分析

笔者旨在建立一种实时变化的网络，通过公交车辆在路网上的位置随时间的变化而延伸得到。分析网络的拓扑结构时，通过调整公交调度策略使整个网络达到稳定。由于公交运营过程中受到较多的因素干扰，为建模和研究方便，建立公交加权网络模型时做如下假设：

1)假定网络中各公交线路的始发站与其后续站点之间总存在车辆服务，且乘客在首站的最短候车时间即为对应公交线路的发车间隔；

2)假定乘客在除始发站外的其余站点的候车时间不超过发车间隔的最大值，即小于等于25 min；

3)公交车辆与乘客到站车站的时间[8]是相互独立的，且车辆的停靠时间服从威布尔分布[9-10]，乘客的到达率服从均匀分布。

文中模型中所构建为虚拟的城市公交线网，调查获取真实的客流数据具有很大难度，因此依据客流的规律特性进行加载，选取工作日平峰和晚高峰两个时段的客流特点作为参考。假定仿真时刻间隔为30 s，进而确定任一仿真时刻各公交线路站点的客流OD矩阵，其中矩阵元素为30 s内到达站点的站间客流量。公交网络模型中各公交线路单位站点的客流OD矩阵如表1。

表1 公交线路单位站点的客流OD矩阵

为更好地分析公交动态网络结构的基本特性，笔者构建了由30条公交线路共100个站点组成的公交网络，当网络中两站点存在公交服务则这两节点之间存在连接线，其具体分布结构如图3。当用MATLAB软件进行仿真分析，设定仿真步长为30 s，仿真时间为16 500 s，最终得到550组不同时间节点的网络不均衡性指标，进而得到平峰和高峰客流下P值的变化情况(图4)。

图3 城市公交网络拓扑结构简化Fig.3 Simplified diagram of urban public transport network topological structure

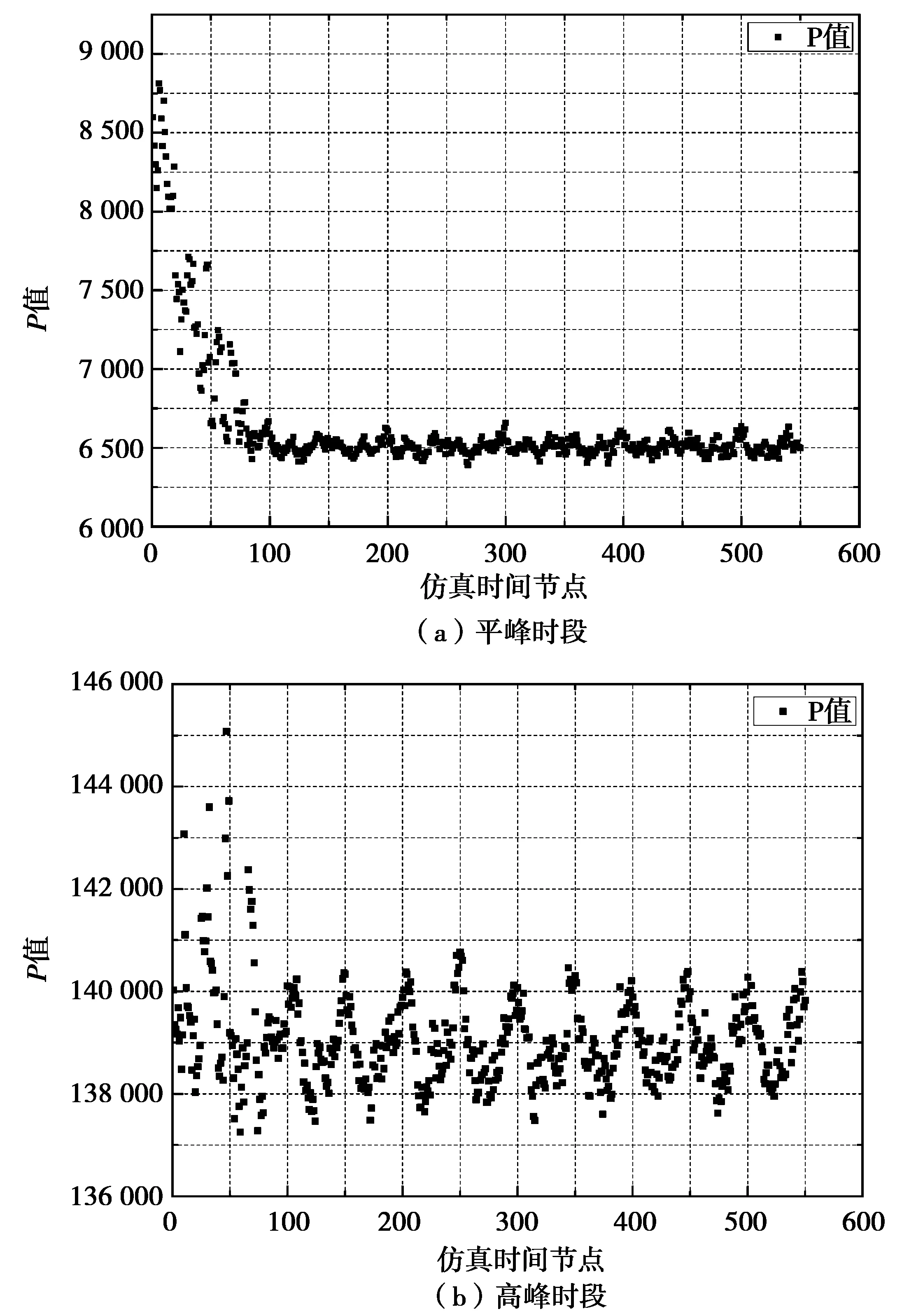
图4 城市公交网络P值变化曲线Fig.4 P value variation diagram of urban public transport network

由图4可知：平峰时段网络中公交运营车辆数越少，P值越大，随着车辆数趋于稳定时，P值逐渐减小至相对稳定状态，也即是提高公交线路车辆的发车频率、缩小发车间隔对降低P值有正向作用；在高峰时段内，随着仿真时间的推移，P值在一定的范围内波动，数值较大且没有明显的降低的趋势，故高峰时段内仅通过提高运营公交车辆数对减小P值作用不大，还应结合科学的公交调度策略，以寻求最佳调度模式。

3 发车频率优化模型

3.1 正班车发车频率优化模型

现有的公交调度相关研究中[11-14]，通常情况下公交网络的控制目标不仅包含乘客等车的时间成本，还应考虑公交运营部门的经济成本，并以此为约束对公交车辆资源进行优化配置。笔者从优化公交网络的节点稳定性角度出发，以不均衡性指标P表征网络中各节点间的差异性，通过优化公交网络中各条线路发车频率，实现网络节点的差异性最小化，进而达到公交网络的最优化状态。

为便于研究，对模型的目标函数和约束条件做出如下假设：

1)不考虑信号交叉口、拥堵排队等客观因素对车辆行车时间的影响；

2)车辆在公交线网中任意两相邻站点间的运行时间一定；

3)不考虑公交车辆的载客容纳量，及乘客在公交站点的滞留时间；

4)乘客在公交站点的候车时间不超过车辆发车间隔，否则认为选择其他出行方式；

5)只考虑车辆单边运行情况。

从网络的层面研究公交车辆与客流OD匹配性，通过对影响P值的线路发车间隔、配车数及其相互关系的分析，建立发车频率优化模型为：

(6)

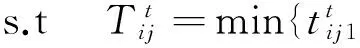
(7)

(8)

(9)

此模型最重要的是包括车辆最短到站时间的约束处理与节点强度计算的处理，下面分别介绍其处理方法。

3.1.1 车辆最短到站时间的处理方法

最重要的约束处理是车辆最短到站时间约束。以单条公交线路而言，当车辆速度固定时，车辆到站时间也确定了。假定站点的位置为Li、线路的运行速度为vn、车辆在站点的停靠时间为Ts、线路发车时刻为T0。则在Tt时刻，这条线路上最快到达站点i的车辆x的行驶时间如式(10)：

(10)

式中：m为车辆x已经过的站点数目；y为从Tt时刻车辆x达到站点i需经过的站点数目。

3.1.2 节点强度的处理方法

节点强度定义为某站点公交车辆到达的最短时间与在此站点等候乘车的乘客数之积，同时可得到不均衡系数P，其计算如式(11)：

(11)

发车间隔影响车辆在路网中的位置，从而影响网络中某一时刻各站点的等车时间。基于此，模型求解主要采用枚举法。其具体步骤如下：

Step1依据公交站点客流OD矩阵，给定各站点等车人数的初始状态。

Step2根据最大配车数，确定每条公交线路的发车间隔区间及网络中运营的车辆数，得到n中发车间隔组合方式。

Step3初始化第一种发车间隔组合S1，利用车辆位置，求出其最短到站时间，确定每个站点的节点强度，得到不均衡系数P1。

Step4调整发车间隔组合，依次得到n组不均衡系数：P1,P2,…,Pn。

Step5比较P1,P2,…,Pn；最小的P值所对应的发车间隔组合即为最优值。

3.2 实例分析

以上述100个公交站点为基础，以线路1、2为例，不考虑其他线路的影响，此两条线路的站点位置如表2。假定公交线路1、2的总长度均为12 km，相邻站间距均为1 km，公交车辆的运行速度定义为6 m/s，站点停靠时间服从函数分布Ts=wblrnd(60, 15)。

表2 公交线路1、2站点及车辆分布

各站点的等车人数如表3，参考站间乘客到达率矩阵，并结合模型相关假设，可以得到公交线路1、2各相邻站点之间的客流OD。

表3 高、平峰时段线路1、2各站点的等车人数

选取公交车辆配车数最大时对应的发车间隔，作为公交线路在高峰时期的最小发车间隔，假定最大发车间隔为10 min；平峰时段的最小和最大发车间隔分别定义为8、15 min。由此得到高、平峰时段的线路发车间隔范围及线路1、2的运行车辆数如表4。此外，对于两条线路的交叉站点，乘客还应考虑两条线路中的最短到站时间。

通过组合线路1、2的发车间隔，平峰时段共有64种组合方式，高峰时段共有42种组合方式，由此得到高、平峰时段所对应的公交网络的不均衡性指标P的变化曲线，如图5，此两条公交线路的最优发车间隔和配车数以及最小P值Pmin如表5。

表4 公交线路1、2发车间隔范围及对应运行车辆数

图5 不同发车间隔对应的公交网络P值变化曲线Fig. 5 P value variation curve of bus network corresponding to different departure intervals

时段线路名称发车间隔/min配车数/辆Pmin平峰时段1路2路885524560高峰时段1路2路587550533

4 结 论

1)在既有公交动态网络建模基础上，考虑车辆位置和站点客流，定义了动态公交网络的邻接矩阵，并建立了面向客流需求的公交动态网络模型；

2)提出了车辆分布与客流不均衡性的评价指标，以构建的公交网络为基础，考虑客流加载方式，研究了不同仿真时段评价指标的变化形式；

3)笔者以网络评价指标为研究对象，建立公交线路发车频率的优化模型，并结合实例进行验证分析，旨在为公交车辆调度提供一定的依据。

[1] LATORA V, MARCHIORI M. Is the Boston subway a small-world network? [J].PhysicalStatisticalMechanics&itsApplications, 2002, 314(1/4):109-113.

[2] 黄爱玲．公交客流加权复杂网络结构及动力学行为研究[D]．北京：北京交通大学，2014． HUANG Ailing.StudyonStructureandDynamicBehaviorsinWeightedComplexPublicTransitNetworkBasedonPassengerFlow[D]. Beijing: Beijing Jiaotong University, 2014.

[3] 高自友，赵小梅，黄海军，等．复杂网络理论与城市交通系统复杂性问题的相关研究[J]．交通运输系统工程与信息，2006，6(3)：41-47． GAO Ziyou, ZHAO Xiaomei, HUANG Haijun, et al. Research on problems related to complex networks and urban traffic systems [J].JournalofTransportationSystemsEngineering&InformationTechnology, 2006, 6(3): 41-47.

[4] 袁春岭．不同调度模式下公交网络复杂性研究[D]．合肥：合肥工业大学，2013． YUAN Chunling.StudyontheComplexityofPublicTransportationNetworkunderDifferentSchedulingModes[D].Hefei:Hefei University of Technology, 2013.

[5] 王锟．基于复杂网络的公交车辆动态分布状态识别与控制策略[D]．合肥：合肥工业大学，2014． WANG Kun.DynamicIdentificationandControlStrategyofBusDistributionBasedonComplexNetworkMethod[D].Hefei:Hefei University of Technology, 2014.

[6] 郑健琛．加权城市公交网络复杂性研究[D]．成都：西南交通大学，2013． ZHENG Jianchen.ResearchontheComplexityofWeightedUrbanBusNetwork[D]. Chengdu: Southwest Jiaotong University, 2013.

[7] 王胜萍．面向客流需求的公交动态网络特征机理研究[D]．合肥：合肥工业大学，2015． WANG Shengping.StudyonCharacteristicMechanismsofBusDynamicNetworkOrientedbyDemandofPassengerFlow[D]. Hefei: Hefei University of Technology, 2015.

[8] 胡华，高云峰，刘志钢．基于AVL数据的公交到站时间实时预测模型[J]．重庆交通大学学报(自然科学版)，2012，31(5)：1014-1017． HU Hua, GAO Yunfeng, LIU Zhigang, Dynamic prediction model of bus arrival time based on AVL data [J].JournalofChongqingJiaotongUniversity(NaturalScience), 2012, 31(5): 1014-1017.

[9] 侯文宇．BRT停靠时间的统计估算研究[J]．山西建筑，2014，40(15)：2-4． HOU Wenyu. The research of statistical estimation and distribution about BRT dwell time[J].ShanxiArchitecture,2014,40(15):2-4.

[10] ZHANG Jian, BAI Haijian. Statistical analysis of the dwell time in a bus station [J].CotaInternationalConferenceofTransportationProfessionals, 2015, 7(1): 1430-1439.

[11] 赵安岭．基于公交动态客流OD的车辆调度优化模型研究[D]．重庆：重庆交通大学，2014． ZHAO Anling.StudyontheOptimalBusVehicleDispatchingModelBasedonDynamicOD[D].Chongqing: Chongqing Jiaotong University, 2014.

[12] 吕林剑．基于公交乘客流构成的公交调度优化模型[D]．成都：西南交通大学，2012． LV Linjian.ResearchonPublicTransitDispatchOptimizationBasedontheCompositionofPublicTransitPassengerFlow[D].Chengdu:Southwest Jiaotong University, 2012.

[13] 李细霞．公交线路车辆调度优化模型研究[D]．武汉：华中科技大学，2007． LI Xixia.StudyonModelsofOptimizingPublicTransportationDispatching[D].Wuhan: Huazhong University of Science and Technology, 2007.

[14] 徐瑜婷，宋瑞，郑锂．区域公交的多车场车辆调度优化[J]．重庆交通大学学报(自然科学版)，2013，32(2)：258-262． XU Yuting, SONG Rui, Zheng Li, Optimization of vehicles dispatching model for multiple depots in regional traffic [J].JournalofChongqingJiaotongUniversity(NaturalScience), 2013, 32(2): 258-262.

(责任编辑：刘韬)

OptimizationofPublicTransportServiceFrequencyBasedonBusDynamicNetwork

ZHANG Weihua, WU Zhenyu, BAI Haijian, WANG Shengping

(School of Automotive and Transportation Engineering, Hefei University of Technology, Hefei 230009, Anhui, P.R.China)

Taking the bus station as the node of dynamic network, the influence of vehicle distribution and passenger demand for bus stops on the balance of public transport network service was mixed to build the bus dynamic network model, which took the passengers’ total waiting time at stops as its edge weight. Then the corresponding relationship between bus network service and bus dynamic network structure was established. On this basis, the space and time balance of the dynamic network was set as the objective, and the network state recognition mechanism was built. Besides, the temporal and spatial variation rule of bus dynamic network was analyzed under the condition of peak passenger flow and flat peak. Finally, taking the time and space balance of dynamic network as the optimization goal, the ordinary line service frequency optimization model was established. Through the computation of case studies, it is found that the proposed model can obtain the optimal service frequency of ordinary line under the steady state network, which provides a new train of thought for the research of public transport scheduling.

traffic engineering; bus passenger flow; bus dynamic network; bus scheduling; service frequency

U492.2

：A

：1674-0696(2017)09-091-07

10.3969/j.issn.1674-0696.2017.09.17

2016-06-12；

：2016-09-14

国家自然科学基金项目(51578207)；国家自然科学青年基金项目(51308176，61304195)

张卫华(1967—)，男，安徽宿松人，教授，博士生导师，主要从事交通规划方面的研究。E-mail：ahweihua@163.com。

吴镇宇(1993—)，男，安徽合肥人，硕士研究生，主要从事交通规划方面的研究。E-mail：125217958@qq.com。