汽车ACC系统算法仿真研究

熊 坚，王秀圣，刘 丁

(昆明理工大学 交通学院，云南 昆明 650500)

汽车ACC系统算法仿真研究

熊 坚，王秀圣，刘 丁

(昆明理工大学 交通学院，云南 昆明 650500)

巡航车辆的跟随特性和安全车距控制是ACC控制系统算法的核心。ACC算法采用分层式控制结构，以线性二次型算法为上层控制器核心，根据传感器测得车辆信息进行运算，通过间距控制策略和控制算法得到期望加、减速度；下层控制器以逆车辆动力学为基础，以MATLAB为平台建立节气门和制动力控制模型，得到期望节气门开度和制动力，实现车辆加速、减速运动控制。通过MATLAB和CarSim联合仿真方式进行仿真实验，对经典线性二次型算法、改进线性二次型算法、综合线性二次型算法3种算法的间距策略进行仿真研究对比。对比3种算法的优缺点，并进行“走-停”工况进行验证。实验结果表明：改进后的算法更适合车辆自适应巡航特点，具有良好的平顺性与安全性，尤其较紧急制动工况下，停车平稳，提高了乘员舒适性与安全性。

车辆工程；汽车ACC；线性二次型控制算法；仿真实验；车辆安全

0 引 言

汽车自适应巡航(ACC)控制技术是先进汽车智能驾驶辅助技术之一，是新一代汽车驾驶智能辅助系统。它根据传感器测得车辆信息并进行间距策略判断，然后通过最优算法得到车辆期望的加、减速度，再通过车辆纵向动力学模型控制车辆加速、匀速、减速，并保持自车与前车的安全车间距，实现车辆自适应巡航的功能。汽车自适应巡航控制技术可降低驾驶员驾驶负担，减少交通事故发生，缓解交通拥堵问题[1]。

汽车ACC控制算法的控制品质，需通过车辆速度、位移、车距的跟随性方面进行评价[2]。目前，许多研究结构和汽车企业正在加快对汽车ACC系统的研究和开发，其控制算法为研究重点[3-4]，CHAN Yuenfong等[5]认为PID是经典的控制方法，并不需要非常精准的控制模型，同时设计算法和控制结构简单，适用于工程控制，在FPGA中广泛应用，同时可以兼顾决策和控制。朱丽丽等[6-8]对PID算法在ACC控制系统中的应用已有深入研究，发现对于ACC系统，其控制结构简单、便于实现等优点。

吴利军等[9]将LQR应用于汽车ACC控制系统，以巡航车辆与前车之间的速度与位移之间的关系，将LQR分为以车距控制和相对车速控制为目的的两种控制模式，并根据两车之间的速度关系实现两种模式的切换，以此生成更接近驾驶员行为的车辆控制目标。宾洋[10]基于LQR最优控制理论，重新构建纵向动力学模型，使得系统对车距控制更加精准，并改善胞核函数控制方式，能很好的抑制系统振动，提高系统抗扰动能力，改善动态品质。张振东[11-13]等将模糊PID算法在ACC系统上的应用进行深入的研究，将模糊算法和经典PID算法相互改进完善，使其具有两种算法所各自拥有的优势，同时又相互弥补两种算法的不足之处。模糊PID控制下的ACC系统控制效果更加突出，使其控制车辆跟随效果突出，在制动和加速中过程更加平顺，更加舒适。

由于最优控制系统就是使系统性能指标达到最优，线性二次型的线性反馈可以构成闭环最优控制系统，可兼顾多项性能指标，并且结构简单。笔者着力于在线性二次型算法状态反馈增益上增加缓和函数的方式，改进LQR算法，提高LQR算法的平缓控制特性。

1 车辆动力学系统建模

1.1 车辆模型

汽车ACC控制系统根据设计需求的要求，为实现各项功能精准的设计和实现，以及对汽车ACC控制系统仿真结果的评判，必须以精准的车辆动力学模型为设计基础。笔者根据已有的强非线性车辆动力学模型计算，推导整个控制方程，建立逆纵向车辆动力学模型。依靠CarSim软件创建精准的车辆动力学模型，并以此为基础建立上层控制算法，为实现整个控制系统的闭环仿真验证提供下层基础[14]。

根据整车参数，利用CarSim中的图形用户界面，建立合理的整车模型。在设定整车及各大系统时，也根据实际的车辆参数进行设定。通过查找资料选定125 kW的发动机，并依据发动机选定125 kW的液力变矩器；同时选用6速一体自动变速器，传动比为1:1；制动系统选用带有ABS的制动系统；悬架为前后都为独立悬架，轮胎选用215/55R17，其滚动半径为335 mm。相关参数如表1。

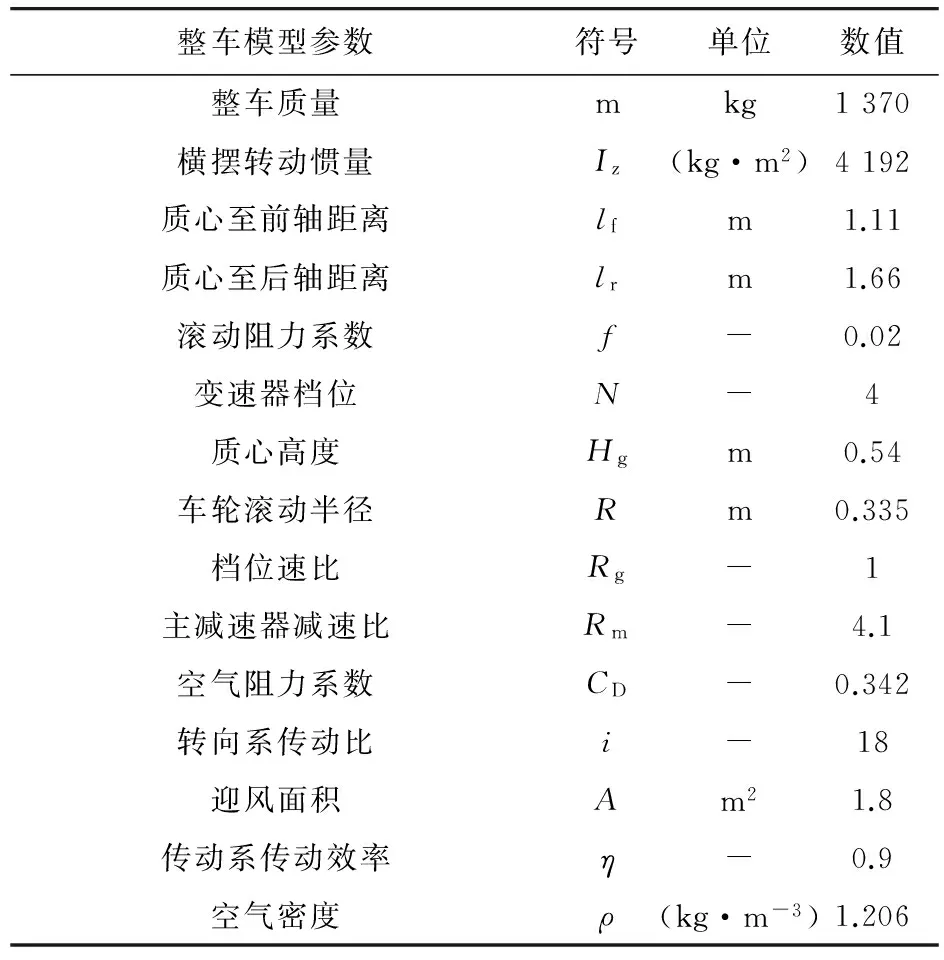
表1 模型参数Table 1 Parameters model

1.2 车辆动力学模型建立

在车辆动力学建立的过程中，可以通过CarSim中的整车参数设计建立整车模型，然后再根据变速器参数建立合适的变速器模型，根据实际制动系统的参数选择合适的制动模型，同样根据转向系的参数建立合适的转向模块，以此选择和设定合理的模型；而一些其他控制系统的逆动力学模型则通过MATLAB建立，如节气门控制模型和制动力控制模型[15]。

Ma=Ft-Fxb-∑F(v)

(1)

式中：Fxb为制动器制动力，N；M为整车质量，kg；a为汽车加速度，(m·s-2)；F(v)为车辆各种阻力的总和，N。

1.2.1 发送机节气门开度与车辆加速的关系

在整个设计的过程中，因为车辆的强非线性，对整车模型进行简化，则驱动力可表示为

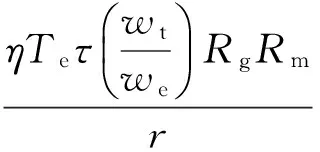
(2)

式中：wt为涡轮转速，(r/min)；we为发动机转速，(r/min)；Rg为变速器档位速比；Rm为主减速器减速比；Te为发动机输出扭矩，(N·m)；r为滚动半径，m；τ为液力变矩器扭矩特性系数。

依据动力学公式获得期望发动机转矩，通过查表求得对应节气门开度：

Ft=KdTe

(3)

(4)

(5)

αdes=f(Te,we)

(6)

式中：α为发动机节气门开度;Ft为由于地面反作用力(左右轮之和)，N；αdes表示期望的节气门开度，f(Te,we)为逆发动机扭矩特性函数。根据已知的不同转速，以及分别对应的不同扭矩下的节气门开度值，可得到一个逆发动机模型的Map图，最终求得期望节气门开度值。下层控制器中节气门控制模型，通过MATLAB/Simulink完成模型建立。

1.2.2 制动压力与减速度的关系

通过上层控制器计算获得期望减速度，下层控制器依据期望减速度计算车辆制动系统中油路的制动压力，最后将制动压力通过车辆4个制动蹄，将制动力施加于车辆刹车片，实现车辆的制动降速。通过上述公式(1)可推导出期望制动压力Pdes：

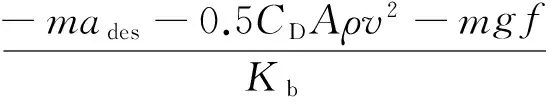
(7)

式中：Pdes为期望制动压力，N；CD为空气阻力系数；f为滚动阻力系数；Kb为制动力和制动压力的比值，经计算得到Kb=1 346。

依据实际客观条件，制动力不可大于地面最大制动力，同时制动力可以简化为制动油路的压力，表达式如式(8)、式(9)：

(8)

(9)

式中：Pb为实际制动压力，N；Tbf为前轮制动力矩，(N·m)；Tbr为后轮制动力矩，(N·m)；根据对应以上的数学模型通过MATLAB建立相应汽车逆纵向动力学模型。

2 ACC系统跟车时距控制算法研究

2.1 ACC系统分析及控制结构设计

文中ACC算法采用分层式控制结构，以线性二次型算法为上层控制器核心，根据传感器测得车辆信息进行运算，通过间距控制策略和控制算法得到期望加、减速度；下层控制器以逆车辆动力学为基础，以MATLAB为平台建立节气门和制动力控制模型，得到期望节气门开度和制动力，实现车辆加速、减速运动控制。

2.2 典型控制目标分析

根据对自适应巡航运行工况的分析，取期望车距和实际车距之差为相对车距误差：ex=ddes-dr，dr两车实际相对距离；相对车速：ev=vf-vh，vf和vh分别为前车和自车速度。同时定义期望车距为ddes=thvf+d0，d0为两车都停止后的安全车间距，th为用户设定期望车间时距。

根据巡航车辆和前车之间的相对速度、相对距离以及两车之间的运动状态来建立车辆间的运动状态空间方程：

(10)

状态向量xT=[exev]，输入量u=ah是自车加速度，扰动量ε=af是前车加速度。

2.3 线性二次型(LQR)及改进算法分析

LQR(linear quadratic)线性二次型最优控制器是以状态方程给出的线性方程为对象，而目标函数为对象状态和控制输入的二次型函数。二次型问题就是在线性系统的约束条件下，选择适当的控制输入，使得二次型目标函数最小[16]。

2.3.1 经典LQR算法

二次型性能指标为

(11)

式中：Q为n×n半正定实对称常数矩阵；R为r×r正定实对称常数矩阵，为使系统所满足上述要求，必须求取u(t)，控制指标函数达到最小。根据Riccati代数方程[17]：

PA+ATP-PBR-1BTP+Q=0

(12)

u=-KX=R-1BTP

(13)

则可得到状态反馈向量k：

K=R-1BTP

(14)

通过以上可以看出，整个二次型控制指标取决于x(t)和Riccati方程的解P(t)，但是P(t)的求解是非常难的，再基于现实这种方程下求解就更加难以实现，所以我们通过现有的工具来实现。通过在MATLAB中调用线型二次型最优模块，进而求取所需要的值[18]:

[KPE]=lqr[ABQR]

(15)

通过推导得到性能指标最小的K：

ades=Kx0ex+Kv0ev

(16)

加速度限制在-8.5～8.5 m/s2之内。

2.3.2 改进LQR算法

改进的LQR算法可以有效的缓解车辆速度冲击过大，并且使系统保持快速的响应，改变形式如式(17)、式(18)：

(17)

(18)

根据控制系统状态可控性判据可知，该系统状态完全可控。利用最优跟踪问题的求解方法，可导出如式(19)：

ades=Kxex+Kvev

(19)

2.3.3 综合LQR算法控制策略

根据跟车时距的大小变换控制算法，能够满足人们对于ACC系统灵敏度与平顺性平衡的要求[19]，为避免经典和改进线性二次型两种算法的频繁切换，设置合理的过渡区域，这样既保持经典LQR控制的优点，也拥有改进LQR的优点。具体设置如下：

当ades≥a+Δh时，经典LQR控制

当ades≤a-Δh时，改进LQR控制

通过MATLAB/Simulink创建选择控制模型，当Th-Tt≥1+0.2时，经典线性二次型控制，实现车辆控制；否则，输出0。当Th-Tt≥1+0.2时，改进LQR控制，将改进的线性二次型算法的期望加速度结果作为输出到下层控制器，实现车辆速度和距离控制；否则，输出0。

3 线性二次型算法仿真分析

对整个控制模型进行联合仿真分析评价，通过CarSim建立前方引导车辆的运行速度模型。前方引导车辆速度模型如图1，车辆速度以55 km/h在原点出发，然后减速到45 km/h，并保持5 s，再加速到60 km/h，保持5 s，再进行减速，并在35 s进行紧急制动，直至车辆速度为0。整个仿真时间为50 s，道路设置为直道。

图1 前车车速Fig.1 Front vehicle speed

3.1 经典LQR算法仿真分析

仿真结果如图2，自车与前车跟随效果分析。

图2 仿真结果Fig.2 Simulation result

1)通过图2可知，巡航车辆具有良好的速度跟随性，再整个跟随过程中，超调量较小，但因控制算法灵敏度较高，使得巡航车辆的速度和加速度波动较大，使平顺性和乘员舒适性较差。因此，通过分析可知，经典线性二次型控制算法具有良好的速度跟随性，能够满足巡航车辆低速运行要求。

2)通过位移曲线分析可知，在前方车辆进行紧急制动时，巡航车辆也进行了紧急制动，停车后两车相距10 m左右，显示出良好的主动避撞性能。

两车车距在巡航过程中逐渐变大，位移控制效果不理想。

3.2 经典LQR算法与改进算法仿真分析对比

仿真结果如图3，车距误差为实际车距与期望车距之差。

图3 仿真对比Fig.3 Simulation comparison

仿真评价：

1)经典算法巡航车辆具有良好的速度跟随性，再整个跟随过程中，超调量较小，但因控制算法灵敏度较高，使得巡航车辆的速度和加速度波动较大，使平顺性和乘员舒适性较差。因此，通过分析可知，经典线性二次型控制算法具有良好的速度跟随性，能够满足巡航车辆低速运行要求。改进线性二次型算法整个控制过程中，速度跟随性良好，在速度发生突变的情况下，体现出良好的抗干扰能力；位移跟随性方面良好，并且车距变化合理，巡航车辆与前方引导车辆跟随紧密；达到驾驶员对灵敏度和乘坐舒适性的要求。

2)当前方引导车辆发生紧急制动时，经典算法控制下的巡航车辆也进行了紧急制动，停车后两车相距10 m左右，显示出良好的主动避撞性能，但乘坐舒适性较差。在改进算法控制下的巡航车辆，整个制动过程制动缓慢合理，虽在一定程度上能保证巡航车辆的安全性和乘坐舒适性，但是后期制动效果差，并且制动距离稍大，避撞性能较差。

3.3 改进LQR算法与综合LQR算法对比仿真分析

仿真结果如图4。

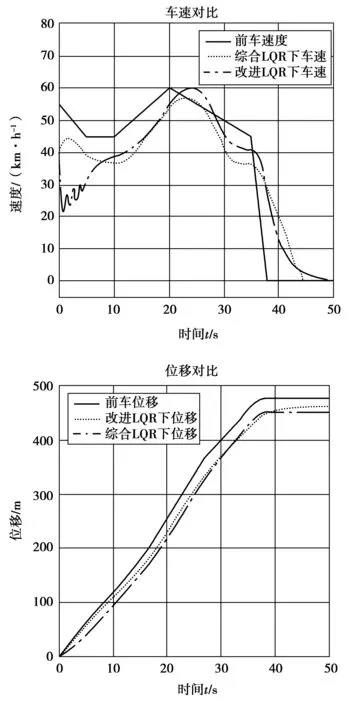
图4 仿真对比Fig.4 Simulation comparison

仿真评价：

1)巡航车辆在跟随过程中，经典算法和改进算法都呈现出良好的速度跟随性，整个过程超调量较小。改进算法控制过程中，达到车辆对灵敏度和平顺性的要求；综合算法控制下的巡航车辆，在速度跟随上稍有滞后，但整个控制过程依然保持在合理的范围之内，灵敏度和平顺性达到平衡。

2)在改进算法控制下的巡航车辆，整个制动过程制动缓慢合理，虽在一定程度上能保证巡航车辆的安全性和乘坐舒适性，但是后期制动效果差，并且制动距离稍大，避撞性能较差。在综合算法控制下的巡航车辆，制动及时，并且制动力都适中，体现出良好的安全性和舒适性，并且具有良好的车辆避撞性能，后期制动合理。

通过对3种控制算法的仿真结果分析可知，综合线性二次型控制算法，具有良好的速度跟随性和位移跟随性，在车辆灵敏度和乘坐舒适性达到平衡。

改进的LQR算法的控制下，拥有良好的乘坐舒适性；经典的LQR算法使得巡航车辆具有良好的响应性能。

3.4 走-停工况仿真分析

因走-停工况是城市交通中比较常见的危险场景，能处理此类紧急状况的自适应巡航车辆也越来越受到人们的关注[20]。本节选用极限工况前车急走急停工况对改进LQR算法进行仿真，验证算法的有效性，走-停工况仿真结果如图5。

图5 走-停工况仿真结果Fig.5 Simulation results of go-stop condition

仿真评价：

在城市“走-停”工况控制过程中，巡航车辆加速缓慢，并且与前方牵引车辆失踪保持合理车距。10 s时前方引导车辆紧急制动，巡航车辆进入紧急制动控制，巡航车辆进行合理的快速跟随；21 s时车辆间车距达到最小2 m；在20 s时前方车辆加速起动，巡航车辆加速缓慢，使得两车间的车距达到理想车距，直至稳定行驶。根据仿真结果可知，在城市“走-停”工况下，巡航车辆具有良好的响应速度，整个控制过程平滑，超调量小，达到算法设计要求。

4 结 语

通过MATLAB和CarSim联合仿真结果分析可知，建立的强非线性逆车辆动力学模型，能够满足系统的要求。

整个控制系统采用分层式控制模式，改进LQR算法与综合LQR控制算法都呈现出量好的控制品质；在设定的仿真工况下，巡航车辆能够准确的跟随前车，并且整个控制过程中车距合理变化，保持在安全车距左右；LQR控制算法控制品质突出，车辆速度跟随性良好，并且使得灵敏度、行驶平顺性、乘坐舒适性达到平衡，体现出良好的避撞性能。

[1] 甘志梅. 基于激光雷达的 Stop & Go 巡航控制技术研究[D].上海:上海交通大学, 2009：20-45. GAN Zhimei. ResearchonStop&GoCruiseControlTechnologyBasedonLaserRadar[D].Shanghai: Shanghai Jiaotong University, 2009: 20-45.

[2] 龚李龙. 车辆自适应巡航控制系统的算法研究[D].杭州:浙江大学,2012：10-36. GONG Lilong.ResearchontheAlgorithmofVehicleAdaptiveCruiseControlSystem[D]. Hangzhou: Zhejiang University, 2012: 10-36.

[3] 黄升宇. 基于模糊MPC算法的自适应巡航控制系统研究[D].长沙:湖南大学,2012：1-50. HUANG Shengyu.ResearchonAdaptiveCruiseControlSystemBasedonFuzzyMPCAlgorithm[D]. Changsha: Hunan University, 2012: 1-50.

[4] 薛玲, 王旭东, 李晓艳,等. 基于PIC16F873汽车巡航控制系统的实验与仿真分析[J].哈尔滨理工大学学报, 2005,10(1):47-51. XUE Ling, WANG Xudong, LI Xiaoyan, et al. Experimental and simulation analysis of PIC16F873 car cruise control system[J].JournalofHarbinUniversityofScienceandTechnology, 2005, 10 (1): 47-51.

[5] CHAN Yuenfong,MOALLEM M,WANG W.Efficient implementation of PID control algorithm using FPGA technology[J].IEEEConferenceonDecision&Control,2005,5(5):4885-4890.

[6] 朱丽丽, 赵秀春.汽车自动巡航系统的PID控制[J]. 科技信息, 2009(34):776. ZHU Lili, ZHAO Xiuchun. PID control of automatic cruise system for automobiles,[J].ScienceandTechnologyInformation, 2009(34): 776.

[7] SERRANO J V Control basado en PID inteligentes: aplicación al control robusto de velocidad en entornos urbano[J].RevistaIberoamericanaDeAutomaticaEInformaticaIndustrial, 2010, 7(4): 44-52.

[8] Minh-Duc Hua, Claude Samson. Time sub-optimal nonlinear PI and PID controllers applied to longitudinal headway car control[J].InternationalJournalofControl, 2011, 84(10): 1717-1728.

[9] 吴利军,刘昭度,何玮. 汽车ACC跟随控制策略研究[J].汽车工程,2005(5):11-14+18. WU Lijun, LIU Zhaodu, HE Wei. Research on vehicle ACC following control strategy[J].AutomotiveEngineering, 2005(5): 11-14+18.

[10] 宾洋,汽车行驶车间纵向距离自适应控制系统的研究[D].重庆:重庆大学,2002. BIN Yang.ResearchonLongitudinalDistanceAdaptiveControlSystemofAutomobileWorkshop[D].Chongqing:Chongqing University, 2002.

[11] 杨振东.基于模糊PID 电子节气门控制系统的研究与开发[D].长沙:湖南大学,2008. YANG Zhendong.ResearchandDevelopmentofElectronicThrottleControlSystemBasedonFuzzy[D].Changsha: Hunan University,2008.

[12] 张强,曲仕茹.车辆自适应巡航控制系统的模糊PID实现[J].汽车工程,2008(7):569-572. ZHANG Qiang, QU Shiru. Fuzzy PID vehicle adaptive cruise control system[J].AutomotiveEngineering, 2008(7): 569-572.

[13] LUO Lihua, LIU Hong, LI Ping, et al. Model predictive control for adaptive cruise control with multi-objectives: comfort, fuel-economy, safety and car-following[J].JournalofZhejiangUniversity(ScienceA), 2010, 11(3): 191-201.

[14] 周晓宏, 刘红军.基于MATLAB的线性二次型最优控制器设计[J].长安大学学报(自然科学版), 2002,22(3):88-90. ZHOU Xiaohong, LIU Hongjun. Design of linear two order optimal controller based on MATLAB[J].JournalofChang’anUniversity(NaturalScienceEdition), 2002, 22(3): 88-90.

[15] 李诗福. 汽车避撞控制系统建模与仿真研究[D].长沙:湖南大学,2009. LI Shifu.AutomobileCollisionAvoidanceControlSystemModelingandSimulationResearch[D].Changsha: Hunan University, 2009.

[16] HUA Minh-Duc, CLAUDE Samson. Time sub-optimal nonlinear PI and PID controllers applied to longitudinal headway car control[J].InternationalJournalofControl, 2011, 84(10): 1717-1728.

[17] KIM S G, TOMIZUKA M, CHENG K H. Smooth motion control of the adaptive cruise control system by a virtual lead vehicle[J].InternationalJournalofAutomotiveTechnology, 2012, 13(1): 77-85.

[18] 毕玉春. MATLAB在线性二次型最优控制器设计中的应用[J]. 齐齐哈尔师范高等专科学校学报,2004(4):125-127. BI Yuchun. Application of MATLAB in the design of linear quadratic optimal controller[J].JournalofQiqiharTeachersCollege, 2004 (4): 125-127.

[19] AUFRèRE R, MARMOITON F, CHAPUIS R, et al. Road detection and vehicle tracking by vision for adaptive cruise control[J].TheInternationalJournalofRoboticsResearch, 2001, 20(4): 267-286.

[20] TSAI C C, HSIEH S M, CHEN C T. Fuzzy longitudinal controller design and experimentation for adaptive cruise control and stop & go[J].JournalofIntelligent&RoboticSystems, 2010, 59(2): 167-189.

(责任编辑：朱汉容)

SimulationofVehicleACCSystemAlgorithm

XIONG Jian, WANG Xiusheng, LIU Ding

(Faculty of Traffic Engineering, Kunming University of Science and Technology, Kunming 650500, Yunnan, P.R.China)

The following characteristics of cruise vehicle and the control of vehicle safety distance are the core of the control system ACC algorithm. ACC algorithm adopted a hierarchical control structure, in which linear quadratic algorithm was taken as the core of the upper controller, and the calculation on the vehicle information measured by sensors was carried out; the expected acceleration and deceleration was obtained through the spacing control strategy and control algorithm; the lower controller was based on inverse dynamics of vehicle, and throttle valve and braking force control model were established on the MATLAB platform. Therefore, the expected throttle valve opening and braking force were obtained, which realized the control of vehicle acceleration and deceleration. Through the combined simulation experiments of MATLAB and CarSim, the comparative simulation research on the spacing strategy among the classical linear quadratic algorithm, the improved linear quadratic algorithm, comprehensive linear quadratic algorithm was carried out. The advantages and disadvantages of the three algorithms were compared and then verified by go-stop condition. The experiment results show that the improved algorithm is more suitable for the characteristics of the vehicle adaptive cruise, with good ride comfort and safety; particularly under emergency braking conditions, parking is steady, which improves occupant’s comfort and safety.

vehicle engineering; vehicle adaptive cruise control system; LQR (linear quadratic algorithm) control algorithm; simulation experiment; vehicle safety

U270

：A

：1674-0696(2017)09-108-07

10.3969/j.issn.1674-0696.2017.09.20

2016-03-17；

：2016-04-21

熊 坚(1959—)，男，四川威远人，教授，博士生导师，主要研究方向为虚拟现实与交通仿真和汽车动力学。E-mail：xjebox@163.com。