数形结合方法在高中数学教学中的应用探究

王菊

数学在各个科学中的地位都十分重要，不仅是由于数学是刻画自然规律与社会规律的重要语言工具，更是由于数学科学的科学性与有效性所决定的，也正是因此，数学有着“科学之母”的美誉。数学在高中阶段是研究空间关系与数量关系的科学，这就决定了数形结合教学法在高中数学教学中广泛运用的理论基础。数形结合法在形式上有助于学生将抽象概括的数学知识与具象的数学图形有机结合在一起，是极为有效的数学学习方式，在高中数学教学过程中，不仅可以使学生进行基础数学知识的构建，还可以加强学生数学能力的培养和数学思想方法的应用。

一、数形结合方法在三角函数定义教学中的应用

在高中数学教学与学习中，有着许许多多的知识点，在这中间“数量关系”、“空间形式”、“数形结合”等是高中数学重点的学习思维方式，在数形结合思想中，高中学生第一个接触的就是三角函数，三角函数不仅仅是函数知识，更是描述周期性的数学模型，从定义上就可以看出三角函数是数形结合思想的产物。如果学生仅依靠代数知识对三角函数进行计算，不仅加大了学生的运算量，还违背了数学计算的简要性原则。假使学生仅依靠图形知识对三角函数进行求导，由于缺乏逻辑与数值进行约束，学生也无法得出三角函数的周期性。因此教师在对学生进行三角函数知识点教学时，就应当为学生引入数形结合法为学生提供思想学习方案，提高学生的数学学习效率、例如：求三分之五π的正弦、余弦和正切值。多数情况下学生仅能依靠已学得的两种定义进行求解，但通过定义法进行学习不利于学生快速求解，当学生计算能力较差时更是容易出错。当采用数形结合法进行学习时可以快速求解，其逻辑过程是这样的：在直角坐标系中在角五分 [y][x][o][A][P（1，y）][图3-1] 之三π上任取点P，画辅助线AP，得到一个三角形Rt△PAO（图3-1所示），通过各点的坐标得出各线段的长度，再根据定义1求解。这就是数形结合法在三角函数中的应用示例。

二、数形结合方法在直线与圆锥曲线教学中的应用

直线与圆锥曲线在高中教学范围内同属于解析几何的知识范畴，同属于近代数学的基础。在这一知识点的学习过程中学生明显会感到不适应，因为在初中阶段的几何问题学习中，几何问题是常量问题并不牵扯变量，但在高中阶段这一情况就发生了巨大变化，几何数学问题中开始充斥着变量给学生带来了巨大的运算量变化的同时也带来的学习困难。而通常数学教师在这一章节中教师最常用的教学法就是“坐标法”，而坐标法所代表的内涵即是数形结合思想。例如：判断直线AB和PQ的位置关系（ ）。A（2，3）B（-1，0）P（1，0）Q（0，-1）在这一问题中学生可以通过方程进行计算，但这样会给学生带来 [y][x][A][B][o][Q][P][2][-1][-1][3][图3-10] 较大的运算量，给学生带来麻烦，而当学生采用数形结合思想的坐标法时，可以进行定点作图（如图3-10所示）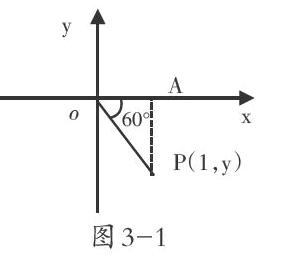

這样的优势在于图形可以绘画的简单明了并便于验证，这种思想及方式不仅为学生带来了便利性的问题解决方式，更是带来了新的问题解决角度。

三、数形结合方法在向量教学中的应用

向量知识在高中知识范围内所涉及的知识点不多也并不复杂，但由于高考试卷中是常考问题其重要性不言而喻。向量知识的起源在于物理学的矢量，这种数字变量的特性在于既有大小又有方向，学生在进行学习时往往无法了解到这一点，经常会在向量的方向学习上出错。这是由于学生是将原有的代数解题法套用到了向量问题中，但由于代数解题法在这种具有多重属性问题中的先天劣势，往往会使学生感到手足无措。当教师采用数形结合法进行向量问题的教学时就会有利于学生对向量问题的理解，从而将向量中的代数关系与几何关系紧密联系起来。在这样的关系结构中不仅可以将向量中的数量关系图形化，更可以将图形数量化，从而打通其二者间的联系。

四、结语

数形结合思想不仅有利于学生解决数学中的几何、代数问题，更有利于帮助学生将二者进行有机联系及转化。学生在初中数学学习中学习的知识多数是直观的具象问题，而高中数学问题多数是抽象化的理念运用问题，当学生可以娴熟运用数形结合方法到数学问题解决中，就可以很轻松地在初中数学与高中数学知识中构建过渡衔接的桥梁。作为教师应当充分发挥数形结合法在数学教学中的优势作用，促进学生数学学习成绩的提高。endprint