地籍测量中直角型房屋界址点坐标的平差计算

赵 梦

(山东省地质矿产勘查开发局第五地质大队，山东 泰安 271000)

·测量·

地籍测量中直角型房屋界址点坐标的平差计算

赵 梦

(山东省地质矿产勘查开发局第五地质大队，山东 泰安 271000)

基于条件平差的函数模型，对地籍测量中直角型房屋的界址点坐标进行了计算，通过所列的条件方程，对含有误差的观测点坐标数据进行了平差计算，得到了各界址点坐标的平差值。计算表明，所得结论具有较好的可操作性和实用性。

地籍测量，直角型房屋，界址点，坐标计算，条件平差

0 引言

在地籍测量中，经常需要进行建筑物界址点的测量，尤其是一些直角型的房屋。利用这些界址点的坐标，从而可以计算建筑物的面积、容积。由于测量误差的存在，实际测量得到的这些房屋界址点的坐标之间不满足直角的几何条件，因此本文基于平行、垂直等几何条件进行了相关的条件平差计算，以求得这些界址点坐标的平差值。

1 理论部分

地籍测量中直角型房屋的形式大体上包括以下几种，如图1所示。图1a)所示形状的建筑物轮廓图，常称为直角型四边形；图1b)所示形状的建筑物轮廓图，常称为直角型六边形；它们都常称为直角型多边形。对于直角型多边形，可以采用多种平差方法进行，本文选择条件平差的函数模型进行了平差计算。

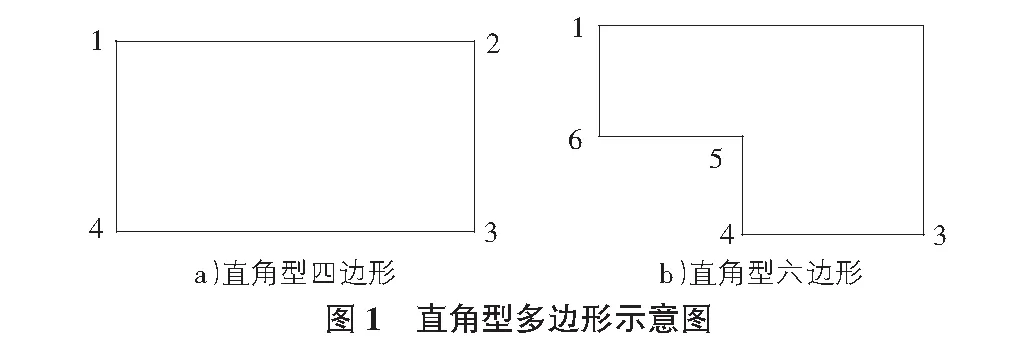
1.1 条件方程的个数及类型的确定

对于图1所示的直角型多边形，设其点的总个数N，则观测值总数n=2N，必要观测数t=N+1，则多余观测数(即条件方程的个数)r=n-t=N-1。

为了确定直角型多边形，还需要列出其条件方程。根据其具有的直角几何关系，可以列出的条件类型包括平行、垂直或同一点两条边的斜率乘积为-1、或同一点两条边的坐标方位角之差为90°，270°。

1.2 条件平差的函数模型

如图1a)所示，设1～4各界址点坐标为(Xi，Yi)(i=1,2,3,4)，则各种条件方程的函数模型如下：

1)平行条件方程。

以边1-2∥边3-4为例，则条件方程为:

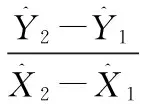
2)垂直条件方程。

以边2-1⊥边2-3为例，则条件方程为:

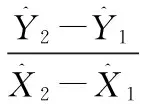
3)直角条件方程。

以点2所在的两条边2-1和2-3为例，两者的坐标方位角之差为90°，则条件方程为：

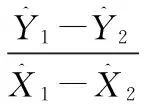
2 实例计算

2.1 实例数据

某测绘单位在一次地籍测量中，需要量测一房屋面积，其相关示意图如图1a)所示。测得该房屋4个角上的坐标观测值(Xi，Yi)，如下所示:

X1=39.943 m,Y1=28.969 m;X2=39.901 m,Y2=35.858 m;

X3=20.362 m,Y3=35.921 m;X4=20.462 m,Y4=28.907 m。

2.2 数据计算

2.2.1 条件方程个数的确定

在该例中，N=4，n=2N=8，t=N+1=5，r=3，即需要列出3个条件方程。

2.2.2 条件方程列立

选取点1～点3所在的边，它们的坐标方位角之差为90°，列出3个直角条件。通过泰勒级数展开，转化为改正数形式为:

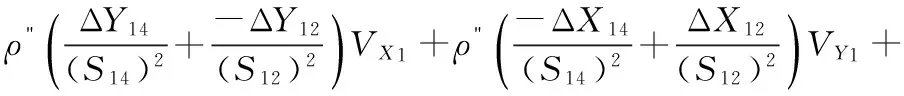
(1)

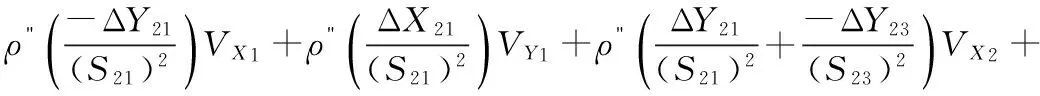
(2)

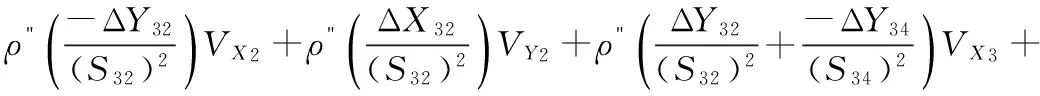
(3)

2.2.3 数据计算

1)各改正数的系数和闭合差。

将已知数据代入式(1)～式(3)，经过计算，可得各改正数的系数和闭合差向量，如表1所示。

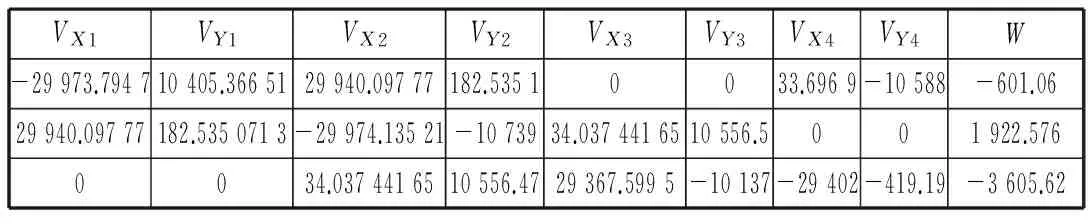
表1 条件方程的各改正数的系数和闭合差向量

2)权的确定。

在此，认为各点的观测精度相同，设它们的权为单位权。

3)各界址点坐标的平差值。

利用最小二乘准则，通过对条件方程进行解算，得出各界址点坐标的平差值如下：

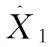
3 结语

以上的计算是基于Excel进行的，计算结果操作可行。同时，文中所提到的函数模型，对于解决地籍测量中界址点坐标的计算具有很强的实用性。但需要注意以下几点：

1)所列的条件方程是非线性的，在进行线性化时舍去了二次以上各项，因此造成了平差后的数据之间的几何条件未改观太大；

2)在进行计算时，要注意单位的换算。

[1] 王 永.利用Excel绘制误差椭圆的方法[J].矿山测量，2008(5):49-51.

[2] 泥立丽.基于Excel的绘制误差曲线的方法[J].矿山测量，2010(3):20-23.

[3] 王 永.Excel应用于《误差理论与测量平差基础》辅助教学[J].中国科技信息，2012(15):141-142.

[4] 翟学敏.Excel在高斯投影坐标正算公式中的应用[J].科技信息，2010(5):44-46.

[5] 苗元欣.基于一元线性回归的变形监测数据处理与分析[J].山西建筑，2013,39(33):206-207.

Vertical-shapehouseboundarypointcoordinationadjustmentincadastralsurvey

ZhaoMeng

(ShandongGeologyMiningSurveyDevelopmentBureau5thGeologyDepartment,Tai’an271000,China)

Based on the function model of adjustment of condition equation, the paper calculates vertical-shape house boundary point coordinate in cadastral survey. Through the listed condition equation, it carries out adjustment calculation of the observation coordination with errors, and obtains the boundary point coordination adjustment value. The calculation shows that: the above-mentioned conclusions has better operability and practicability.

cadastral survey, vertical-shape house, boundary point, coordinate calculation, adjustment of condition equation

TU198.2

：A

1009-6825(2017)24-0189-02

2017-06-11

赵 梦(1984- )，女，工程师