浅水中质量源造波方法

田正林，孙昭晨，梁书秀

(大连理工大学 海岸及近海工程国家重点实验室，大连 116024)

浅水中质量源造波方法

田正林，孙昭晨，梁书秀

(大连理工大学 海岸及近海工程国家重点实验室，大连 116024)

针对质量源造波过程中源区上方水体高度难以确定的问题提出了改进方法，将源区高度值考虑到源强方程中，避免了造波过程中源区上方水体高度值多次试算带来的不便。该方法弥补了质量源造波方法在水深小于1.5 m的浅水中所造波浪与理论波浪之间差距较大的缺陷，尤其是水平网格步长与源区高度值相比小于10的情况，推广了质量源造波方法在浅水中的应用。文中验证了波高对所造波浪的影响以及时间步长对浅水中所造波浪的影响，得出结论：当波高与水深的比值小于0.2时所造波浪波高与理论值的拟合较好；当时间步长小于0.005 s时所造波浪无明显的上下漂浮现象，波形稳定，符合理论波形要求。

质量源造波；浅水造波；源区高度；改进方法

数值波浪水槽是港口海岸工程数值模拟的基础，造波系统与消波系统是数值波浪水槽的重要组成部分，造波系统造波能力及消波系统消波能力又是数值波浪水槽可用性的关键。大多数值模拟采用加长计算域或是波动没有达到准稳定状态时结束模拟避免二次反射波的影响[1]。为了得到长时间稳定的数值模拟，对数值水槽的要求是一能够降低二次反射波，二所造目标波浪不受反射波的影响，流体域内部造波方法能够很好地解决该问题。Larsen和Dancy[2]在水域内部沿一定长度的直线段上通过扰动水面生成目标波浪，避免了二次反射波的影响。

目前，流体内域造波主要有动量源造波和质量源造波。动量源造波是将目标波浪作为人工源项加到动量方程中生成所需波浪场，质量方程保持不变，自由水面以下区域均属造波源区，造波过程中在整个造波源区内施加动量源方程；质量源造波是将目标波浪作为人工源项加到质量方程中生成所需波浪场，造波过程中并不是自由水面以下区域均属造波源区，源区顶部与自由水面之间存在一定高度无质量源的水体，正因为此部分水体的存在使得源区高度的确定变得繁琐。Lin和Liu[3]通过试算得出质量源造波源区中心到静水面之间的距离为13～12水深时所造波浪比较理想。周玲玲，丁全林，兰庆琳等[4]指出质量源距离水面13水深时的模拟结果较为精确，并将此处定义为质量源的标准位置。余勇飞[5]在深水数值水槽造波时质量源区上方水体高度采用一倍波高时所造波浪精度较高，与理论波浪匹配较好。李宏伟[6]在造孤立波时质量源区上方水体高度采用半倍波高时，所造孤立波波形与理论波形匹配较好。Chen和Hsiao[7]在FLOW-3D中开发了水体内域造波质量源区域的设计方法，详细描述了质量源位置的确定公式，为质量源造波方法的应用提供了便利。

已有文献质量源区上方水体高度大多采用试算法确定，只给出经验高度区间，并且试算法的成功快慢取决于个人经验，对于经验不足者尤显耗时。笔者造波过程中发现质量源区上方水体高度为一倍波高时在水深大于1.5 m的深水情况下所造波浪极好，但在水深小于1.5 m的浅水中所造波浪并不理想，尤其是在水平网格步长与源区高度值相比小于10时所造波浪波高与目标波浪波高相差较大，必须不断地加大或减小源区上方水体高度以减小差距。而通常情况下需要造多种波高的目标波浪，这样每次变化波高时都需要不断调整源区上方水体高度，既费时也是没有必要的。故本文针对质量源造波源区上方水体高度难以确定的问题，提出改进方法，避免了多次试算带来的麻烦，进一步完善了质量源造波方法。

1 数值模型

基于FLUENT求解器，求解雷诺平均N-S方程，采用雷诺应力粘性模型封闭方程组。采用有限体积法离散方程，PISO压力速度耦合算法求解离散方程，对流项采用三阶MUSCL格式，用改进的QUICK方法跟踪自由表面。边界条件为左右侧为对称边界条件，底部为墙边界条件，上部为压力进口边界条件。以下仅就文中的控制方程、造波方法及消波方法进行描述。

1.1控制方程

张量形式的连续性方程和动量方程如下

(1)

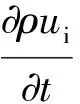
(2)

对于二维问题i,j=1,2；ui,uj为速度；p为压强；ρ为密度；g为重力加速度。粘性应力张量τij为

(3)

μ为分子运动粘性。

1.2造波方法

数值波浪水槽的质量源设置于计算域内，质量源区距离左侧消波区至少一倍波长的距离可以很好地消除波浪二次反射(Lin & Liu[1])，本文造波源区距离左侧消波区2L(L为波长)。

造波源区内质量守恒方程为

(4)

s(xi,t)为质量源强方程，其大小由设计的入射波波面方程决定，造波源区内非零，造波源区外为零。理论上，当质量源宽度远小于波长时，可作点源处理，假定质量源引起的质量增减对应于入射波波面的变化，并且源区内质点的水平速度等于设计波浪的水平速度，因为质量源可以看做均匀分布的点源，所以在造波源域Ω内每个网格中应满足下列关系[5-6，8-9]

s(xi,t)ΔxΔyΔt=2u(xi,t)ΔyΔt

(5)

化简式(5)得下式

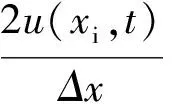
(6)

式中：xi为“源强”的水平位置；Δx为网格的水平尺度；Δy为网格的垂向尺度；右端系数2表示质量源产生传播方向相反的两列波。

二维二阶Stocks 波的水平速度方程如下

(7)

将式(7)代入(6)得源强方程如下

(8)

式中：H为波高；k为波数；ω为频率；D为水深。

以下通过对造波源区域源强方程的改进，可以得到更适合浅水区域的造波方法。造波源区简图如图1所示，造波源区底部为墙边界并无水体向下喷出，考虑单位时间内造波源区其他3个方向喷出的水体质量守恒可推得

s(t)·Δx·Hs=2u·Hs+Δx·v

(9)

式中：u为造波源区流体质点水平速度；v为造波源区流体质点垂向速度；Hs为造波源区高度。化简(9)可得

s(t)=2uΔx+vHs

(10)

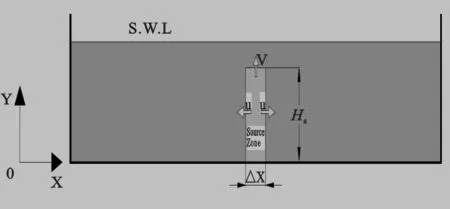
图1 源造波区简图Fig.1 Sketch of the source wave-maker zone

质量源造波假定源区内各点产生的水平速度等于波生成对应点产生的水平速度，造波源区上方水体依靠水体自重形成的恢复力产生波浪，因此源区上方至自由水面高度的确定比较关键。仔细研究方程(10)可以发现：造波过程中u和v的量级相当，由于Δx一般小于波长的5%，非常小，而Hs一般大于23倍的水深，对于水深大于1.5 m的深水Δx相比Hs更为小量，至少小一个量级，式中的第二项对源强的贡献较小可以忽略，但对于水深小于1.5 m的浅水，第二项会随着水深的减小而增大，其对造波源的贡献也会逐渐增大，如果第二项继续忽略会影响所造波浪的波高。数值波浪水槽造波时如果水深小于1.5 m，Hs小于1.0 m，Δx又小于0.1 m，可以看出此时第一项与第二项相比在10以内，不足一个量级，如果水深继续减小，Hs继续减小，式中第二项对源强的贡献会更大，不应忽略。根据Broren.M.,Larsen.J.[10]描述，源造波的原理类似于“水下爆炸”原理，那么源爆炸瞬间质点各个方向的速度大小应该相等。所以质量源向外喷出的流体速度各方向应该大小相等，因此u=v，最终可得源强方程为

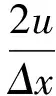
(11)

周玲玲，丁全林，兰庆琳等[4]指出为避免数值振荡，质量源初始时刻应设置为0，二阶Stocks波令初始相位为-π2，并在计算历程开始时刻设置软启动缓慢施加质量源驱动波面变化。本文采用此种做法，最终施加的源强方程如下

图2 源区右侧数值水槽示意图Fig.2 Right side schematic diagram of numerical wave tank

(12)

式中：N为缓变控制参数；t0为缓变时间。

1.3消浪层

为了吸收二次反射波和不需要的源造波，数值波浪水槽左右端应布置至少一倍波长的海绵吸波层耗散波能。本文采用的吸收方程是由Niels and David[11]提出的椭圆方程(13)，x0表示消波层起始点x坐标；xs表示消波层长度，方程从海绵层起点1逐渐减小到海绵层终点0。

图3 实际波形与理论波形的对比Fig.3 Comparisons of present wave elevation and theory wave elevation

海绵层消波方程μ(X)

(13)

数值波浪水槽源区右半侧示意图，如图2所示。

2 数值模拟结果

本文数值波浪水槽长36 m，高0.7 m，水深0.5 m，质量源高度Hs为水深的23，△x小于波长的5%。以下对所造波浪结果、波形沿程变化、波高对目标波浪的影响以及时间步长对波形的影响进行描述。

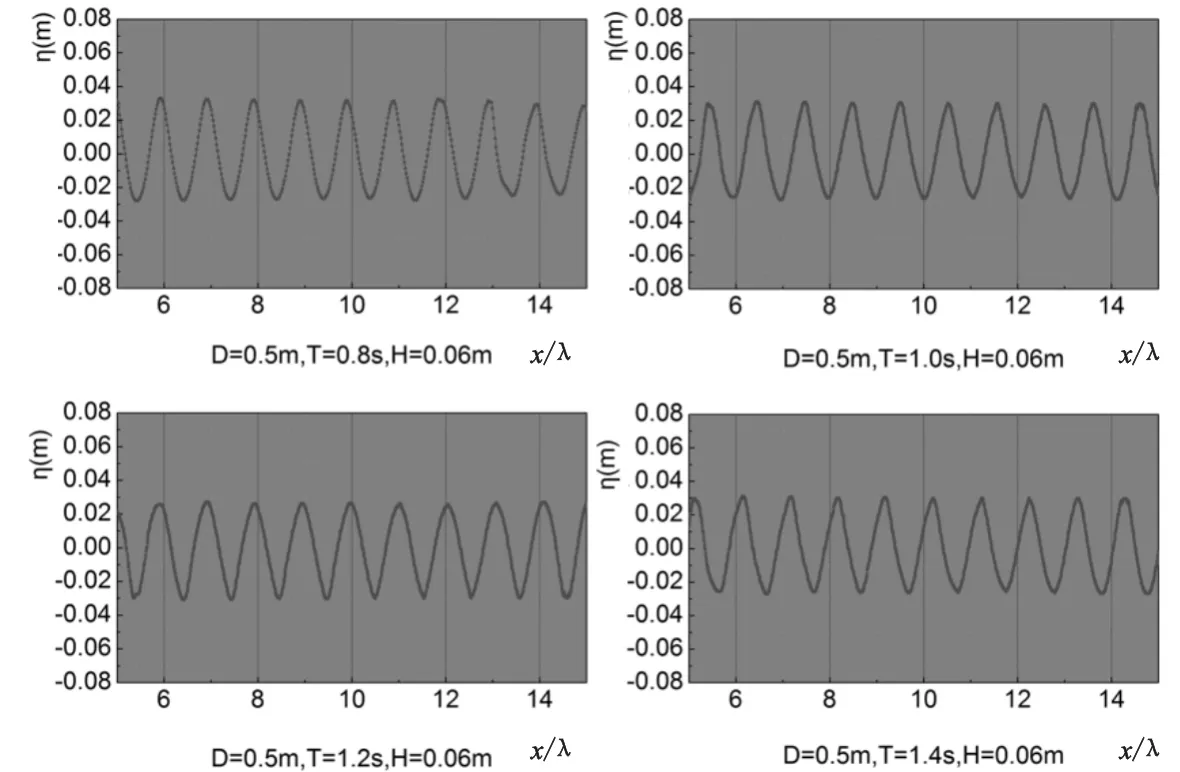
图4 波形沿程变化图Fig.4 Wave elevation displacement of present model with distance from the source zone

2.1实际波形与理论波形对比

为了验证所造波浪的有效性，给出水深D=0.5 m，波高H=0.06 m，周期T分别为0.8 s、1.0 s、1.2 s、1.4 s时的实造波浪波形与理论波浪波形的对比(图3)。从图3中可以看出：不同周期时的实际波形与理论波浪波形匹配较好，虽波谷处振幅值比理论值略小但仍都可以满足精度要求。

2.2波浪沿程变化情况

为了说明波浪沿程变化情况，给出了水深D=0.5 m，波高H=0.06 m，周期T分别为0.8 s、1.0 s、1.2 s、1.4 s时造波源区(约5倍波长处)右侧波浪10倍波长范围内的波浪沿程变化情况(图4)。从图4可以看出：所造波浪沿程衰减较小，满足目标波浪精度要求。

图5 所造波浪波高与理论波高的对比Fig.5 Comparisons of the targeted wave height and theoretical wave height

2.3波高对目标波浪的影响

为了检验改进的质量源造波方法所造不同波高的波浪与理论波浪的差距，本部分计算了D=0.5 m，T=1.2 s，波高H分别为0.06 m、0.08 m、0.10 m、0.12 m造波源区(约5倍波长处)右侧波浪10倍波长范围内的波浪随时间的变化(图5)。从图5可以看出：随着波高的增大，所造波浪波高与理论波高的差距在增大；波高H=0.10 m时所造波浪波高只是在波峰处略小于理论值，波谷处仍与理论值拟合较好，但是当波高H=0.12 m时所造波浪波峰和波谷处均与理论值有偏差，所造波浪效果变差。由此可知当波高与水深的比值超过0.2时所造波浪波高与理论值的拟合较差，所以此种造波方法适合于波高与水深的比值在0.2以下的情况。

2.4时间步长的影响

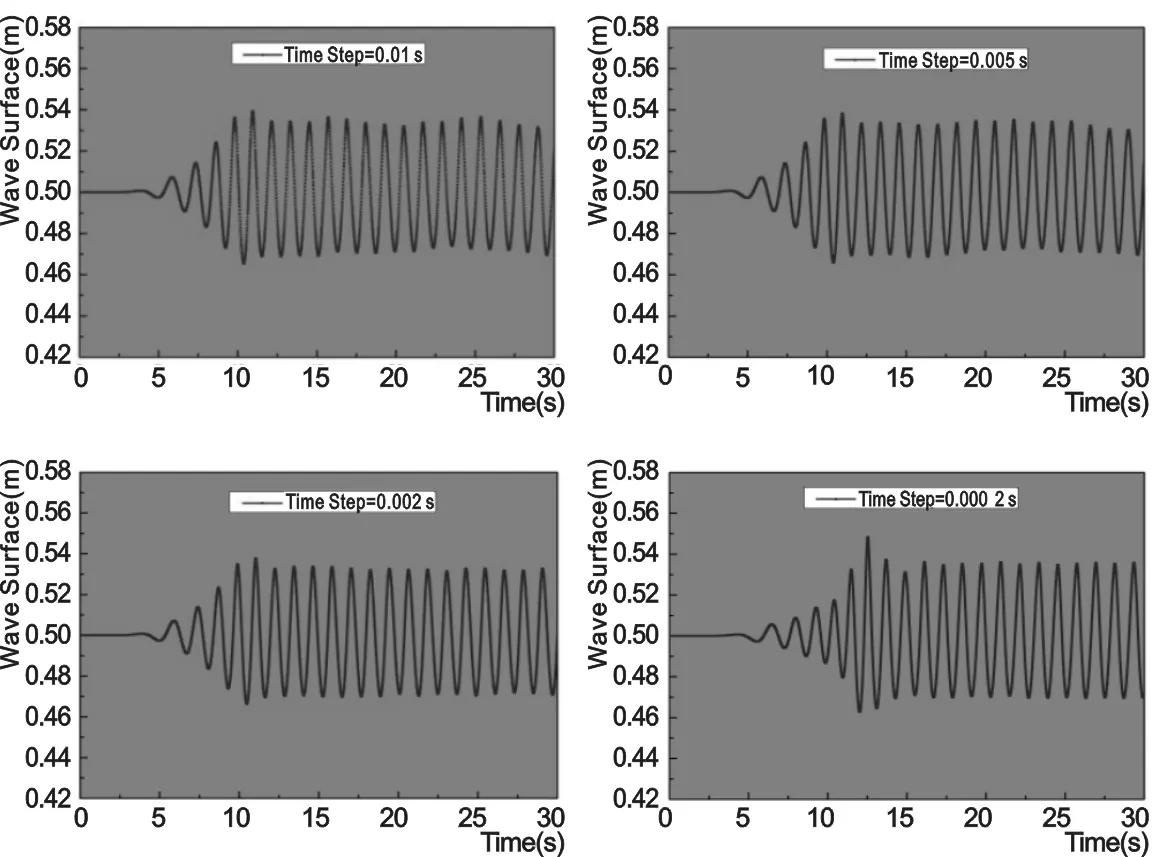
图6 波形随时间变化图Fig.6 Time step effects on wave surface

为了检验时间步长对改进的质量源造波方法所造波浪的影响，给出了水深D=0.5 m，周期T=1.2 s，波高H=0.06 m时所造波浪波形随时间的变化。时间步长验证之前需要对网格进行反复调整验证，当网格连续3次调整后的波形无较大变化后停止，进行时间步长验证。时间步长分别取0.01 s、0.005 s、0.002 s、0.000 2 s进行验证。对比所得波面由图6可以看出：当dt=0.01 s、dt=0.005 s时，随着时间的增长波面出现了幅度较大的上下飘动现象，而当dt=0.002 s、dt=0.000 2 s时，波面已无明显的上下飘动现象，波面较稳定。

3 结论

将质量源区高度值考虑到造波源强方程之中，量化源区上方水体高度，克服了水深小于1.5 m时造波过程中源区上方水体高度难以确定的困难，得到了适合于浅水的质量源造波方法。该方法可以在水深小于1.5 m的浅水中造出比较理想的波浪，更适合于水平网格步长相比于源区高度值小10倍的情况。文中验证了波高对所造波浪的影响、时间步长对浅水中所造波浪的影响及波浪沿程变化，得出结论：当波高与水深的比值小于0.2时所造波浪波高与理论波高值的拟合较好；当时间步长小于0.005 s时所造波浪无明显的上下漂浮现象，波形稳定，符合理论波形要求，波浪沿程衰减较小。

[1]Lin P, Liu L F. Discussion of "Vertical variation of the flow across the surf zone" [Coast. Eng. 45 (2002) 169-198][J]. Coastal Engineering, 2004, 50(3):161-164.

[2]Larsen J, Dancy H. Open boundaries in short wave simulations-A new approach[J]. Coastal Engineering, 1983, 7(3):285-297.

[3]Lin P, Liu L F. Internal Wave-maker for Navier-stokes Equations Models[J].Journal of Waterway, Port, Coastal and Ocean Engineering, 1999,125(4): 207-215.

[4]周玲玲,丁全林,兰庆琳,等.基于LB方法的质量源造波的数值波浪水槽[J].水电能源科学，2015,33(3):99-103. ZHOU L L,DING Q L,LAN Q L, et al.Numerical Wave Tank with Mass Source Generating Waves Based on LB Method[J]. China Civil Engineering Journal, 2015, 33(3): 99-103.

[5]余勇飞.波浪的数值模拟及其流场结构分析[D].哈尔滨：哈尔滨工业大学，2013.

[6]李宏伟.造波理论与方法研究[D].哈尔滨：哈尔滨工程大学，2013.

[7]Chen Y L, Hsiao S C. Generation of 3D water waves using mass source wavemaker applied to Navier-Stokes model[J]. Coastal Engineering, 2016, 109:76-95.

[8]房卓,张宁川,臧志鹏.透空式梳式防波堤的数值模拟和波浪透射系数的研究[J].水道港口,2011,32(2)：86-93. FANG Z, ZHANG N C, ZANG Z P. Numerical simulations of open comb-type breakwater and research on its wave transmission coefficient[J].Journal of Waterway and Harbor,2011,32(2):86-93.

[9]FANG Z, ZHANG N C, ZANG Z P. Experimental and Numerical Study on Hydrodynamic Performance of Impermeable Comb-Type Breakwater[J]. Journal of Ship Mechanics, 2012, 16(6):632-645.

[10]Brorsen M, Larsen J. Source generation of nonlinear gravity waves with the boundary integral equation method[J]. Coastal Engineering, 1987, 11(2):93-113.

[11]Jacobsen N G, Fuhrman D R, Fredsφe J. A wave generation toolbox for the open-source CFD library: OpenFoam[J]. International Journal for Numerical Methods in Fluids, 2012, 70(9):1 073-1 088.

The method of mass source wavemaker in shallow water

TIANZheng-lin,SUNZhao-chen,LIANGShu-xiu

(StateKeyLaboratoryofCoastalandOffshoreEngineering,DalianUniversityofTechnology,Dalian116024,China)

In view of the problem that the distance between the top of the source region and the still water level is difficult to determine in the process of mass source wavemaker, the improved method was proposed in this paper. In the mass source functions took the height of the source region into account, the inconvenience of many trials to get the height of the mass source region can be eliminated in the process of wavemaker. This method remedies the defect that the difference between targeted wave and theoretical wave in the shallow water whose depth less than 1.5 m, especially horizontal grid step is an order of magnitude 10 smaller than the source region height, the mass source wave-maker method is promoted in the shallow water.The effects of wave height and the time step on simulated waves were studied. The conclusions show that the fitting between made wave and theoretical wave is good when the ratio of wave height and water depth is less than 0.2;when the time step is less than 0.005 s, the floating phenomenon of the simulated waves is well controlled, waves surface is stable and conforms to the requirements of the wave theory.

mass source wavemaker; shallow-water wavemaker; height of source region; improved method

TV 139.2

：A

：1005-8443(2017)04-0325-05

2017-01-13；

：2017-04-06

国家自然科学基金资助项目(51279028)；国家海洋局公益性行业科研专项(201405025-1)

田正林(1985-),男，黑龙江省哈尔滨人，博士研究生，主要从事波浪与结构物相互作用的研究。

Biography： TIAN Zheng-lin(1985-),male, doctor student.