魔芋真空干燥特性及动力学模型的建立

黎斌，彭桂兰，吴绍峰，罗传伟，邱光应，杨玲

(西南大学 工程技术学院,重庆,400715)

魔芋真空干燥特性及动力学模型的建立

黎斌，彭桂兰*，吴绍峰，罗传伟，邱光应，杨玲

(西南大学 工程技术学院,重庆,400715)

为了实现魔芋的规模化真空干燥，缩短干燥时间，提高脱水制品的品质，降低生产能耗和成本。该文采用真空干燥技术将其干燥至安全含水率15%，选取温度(50、60、70 ℃)和真空度(0.04、0.05、0.06 MPa)为试验因素进行研究，考察了温度和真空度对魔芋切片干燥水分比MR和干燥速率DR的影响、水分扩散系数以及干燥活化能。利用6种常见食品干燥数学模型对实验数据进行非线性拟合，通过比较评价决定系数R2、卡方χ2、和标准误差eRMSE以及平均相对误差E得到较优模型模型并与BP神经网络模型进行对比检验。结果表明，魔芋切片真空干燥是内部水分扩散控制的降速干燥过程；魔芋真空干燥最佳动力学模型为BP神经网络模型，模型平均相对误差E为1.32%；在不同干燥条件下对魔芋有效扩散系数Deff和活化能Ea进行求解表明，有效水分扩散系数Deff与真空度和温度成正比，平均干燥活化能Ea为28.96 kJ/mol。

魔芋；干燥；模型；真空干燥；动力学

魔芋(konjac)为天南星科(araceae)魔芋属(amorphophallus blume)多年生草本植物[1-2]，原产于亚洲中南半岛北部和云南南部北纬16°～24°地带[3]，我国现已发现和命名的品种有26个。魔芋富含葡甘聚糖、纤维素、淀粉、氨基酸、生物碱、可溶性糖等大量特殊物质，其中葡甘聚糖含量高达60%(干基)，因此魔芋具有丰富的药用和食用价值[4]。由于刚采收的魔芋含水率较高(80%～85%)，使得魔芋贮藏过程中易变质腐烂，干燥是保证其品质和营养价值的重要手段[5]。

农产品在干燥过程中易发生Maillard反应从而引起褐变，干燥温度和干燥时间对农产品颜色变化有很大影响[6-8]，因此魔芋采摘后的快速干燥是很有必要的。目前真空干燥技术被广泛应用于食品行业，TAKAHIRO ORIKASA等[9]运用真空干燥技术分析了猕猴桃切片在干燥过程中水分、硬度、VC含量、抗氧活化性以及色泽的变化。VISHAL KUMAR等[10]在不同热烫时间、热烫温度和干燥温度下对魔芋片干燥动力学及品质特性(色泽、质地、褐变和感官品质)进行了研究，得到魔芋热风干燥的最佳工艺参数。SYARIEF[11]、SADOWSKA[12]等用真空干燥方法对油菜籽进行薄层干燥特性研究，并建立该试验品种的薄层干燥数学模型。

我国对魔芋的干燥技术研究也逐渐受到广泛关注。冯亚运等[13]研究了魔芋气体射流冲击干燥特性，其试验中所采用的切片厚度为3～5 mm，风温为70～100 ℃，风速为10～13m/s，其水分有效扩散系数在1.232 3×10-9～2.217 8×10-9m2/s随着切片厚度、风温和风速的增加而增加；并利用阿伦尼乌斯公式计算魔芋片的干燥活化能，气体射流冲击干燥的魔芋活化能为6.601 kJ/mol；叶维等[14]研究了魔芋热泵干燥特性，并建立了魔芋热泵干燥的数学模型，其最大的特点是考虑了魔芋品质及褐变的问题，在对魔芋干燥前，对魔芋进行了护色处理，且经过护色处理后，魔芋热泵干燥的色泽良好；和智坤等[15]研究了魔芋葡甘露寡糖的干燥加热硒酸化及其产物的抗氧化性，试验表明，葡甘露聚糖硒酸化有利于提高葡甘露聚糖的抗氧化性。

本文将真空干燥技术应用于魔芋干燥，选用真空度和干燥温度2个因素进行全面实验，利用6种经典数学模型拟合试验数据，对经典模型和BP神经网络模型进行对比，得到魔芋真空干燥最佳模型。计算出魔芋真空干燥有效水分扩散系数Deff和干燥活化能Ea，以期能够较准确地预测魔芋真空干燥过程中水分变化规律和干燥速率，为魔芋真空干燥工艺参数选择提供理论依据和实践指导。

1 材料与方法

1.1材料

新鲜白魔芋，一年生，购于四川宜宾市，选择个体完整、无机械损伤、大小均匀的魔芋。

1.2仪器与设备

DZF型真空干燥箱，北京科伟永兴仪器有限公司；KW-2型旋片式真空泵，北京科伟永兴仪器有限公司；JA5002电子精密天平(测量精度为10 mg)，上海精天电子仪器有限公司。

1.3方法

1.3.1 魔芋加工工艺流程

鲜芋→挑选→清洗→去皮→清理→切片→干燥

1.3.2 魔芋真空干燥特性实验方案

真空干燥实验前对干燥仓内进行预加热，减小热惯性对干燥温度造成的影响，根据前期干燥预实验，选取大小均匀、没有质量缺陷的魔芋进行切片处理，洗净削皮后将其切成厚度为4mm的正方形的小块，准确称量(50±0.1) g放置于预先加热的真空干燥箱内进行干燥处理，干燥温度采用50、60、70 ℃，真空度选取0.04、0.05、0.06 MPa进行全面实验。采用间歇式称量，每隔20 min记录一次物料的质量，当干燥至前后2次称量质量差不超过0.10 g时即认为物料达到平衡含水率Me，停止干燥，每组实验进行3次平行试验。

1.3.3 试验各指标

(1)初始含水率的测定

105 ℃恒温干燥法，参考GB /T 5009. 3—2003。

(2)含水率比MR及干燥速率DR

根据水分比定义可得，含水率比及干燥速率计算公式如下：

MR=(Mt-Me)/(M0-Me)

(1)

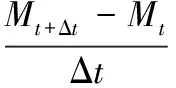
(2)

式中：Me，试样平衡含水率，%d.b.；M0，试样初始含水率，%d.b.；Mt，试样在t时刻的含水率，%d.b.；Mt+Δt：试样在t+Δt时刻的含水率，%d.b.；Δt，时间差值，h。

(3)有效水分扩散系数Deff

在降速干燥阶段，生物制品的干燥特性可以用Fick扩散方程来描述，方程的解法由Crank提出，适用于长方形、圆柱形和球形等形状的物料。当所有的魔芋样品都有相同的初始含水率时，魔芋的有效水分扩散系数可用式(3)来计算[16]：

(3)

式中：Deff为有效水分扩散系数；L0为魔芋片厚度的一半，L0=2 mm。

通过绘制lnMR相对于干燥时间t的曲线，将曲线进行线性拟合，则通过此直线的斜率k可计算出魔芋的有效水分系数Deff。

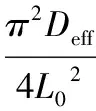
(4)

(4)活化能Ea

有效水分扩散系数Deff与温度T的相关性遵循Arrhenius关系[17],关系式如下所示：

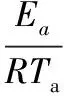
(5)

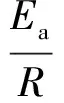
1.4各数学模型评价指标

本实验采用平均相对误差E、决定系数R2、卡方χ2及均方根误差eRMSE4个参数来衡量模型拟合效果的好坏，平均相对误差在研究中被广泛的应用，E值低于10%说明拟合度比较好；R2值越大说明模型拟合效果越好；χ2和eRMSE越小则模型拟合度越高。各评价指标计算式如下：

(1) 平均相对误差E

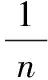
(6)

(2) 决定系数R2

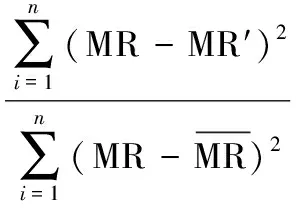
(7)

(3) 卡方χ2

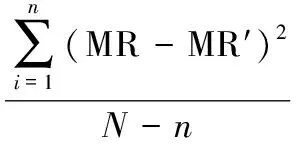
(8)

(4) 均方根误差eRMSE

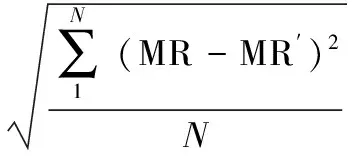
(9)

1.5BP神经网络设计

(1) 输入层节点的选择

将影响魔芋真空干燥综合指标的包括干燥温度、真空度和时间3个因素作为BP神经网络模型的输入节点。

(2) 输出层节点数的确定

将魔芋真空干燥的含水率比作为评价参数，即输出层节点数为1。

(3) 隐含层节点数的确定

根据经验公式可以进行隐含层节点数的选择。经验公式如下：

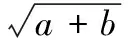
(10)

式中：m为隐含层节点数；a为输入节点数；b为输出节点数；n为1～10之间的调节常数。

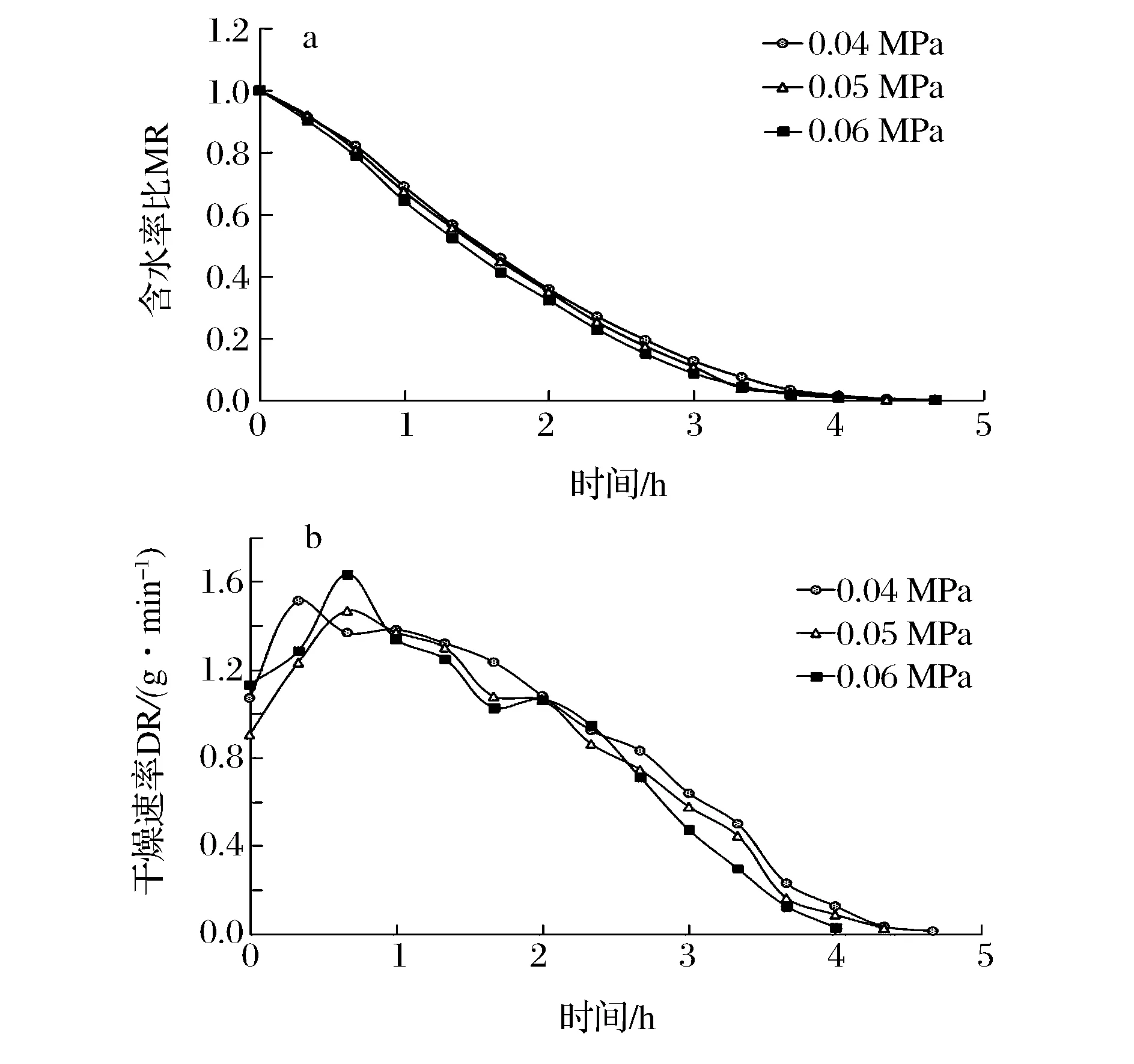
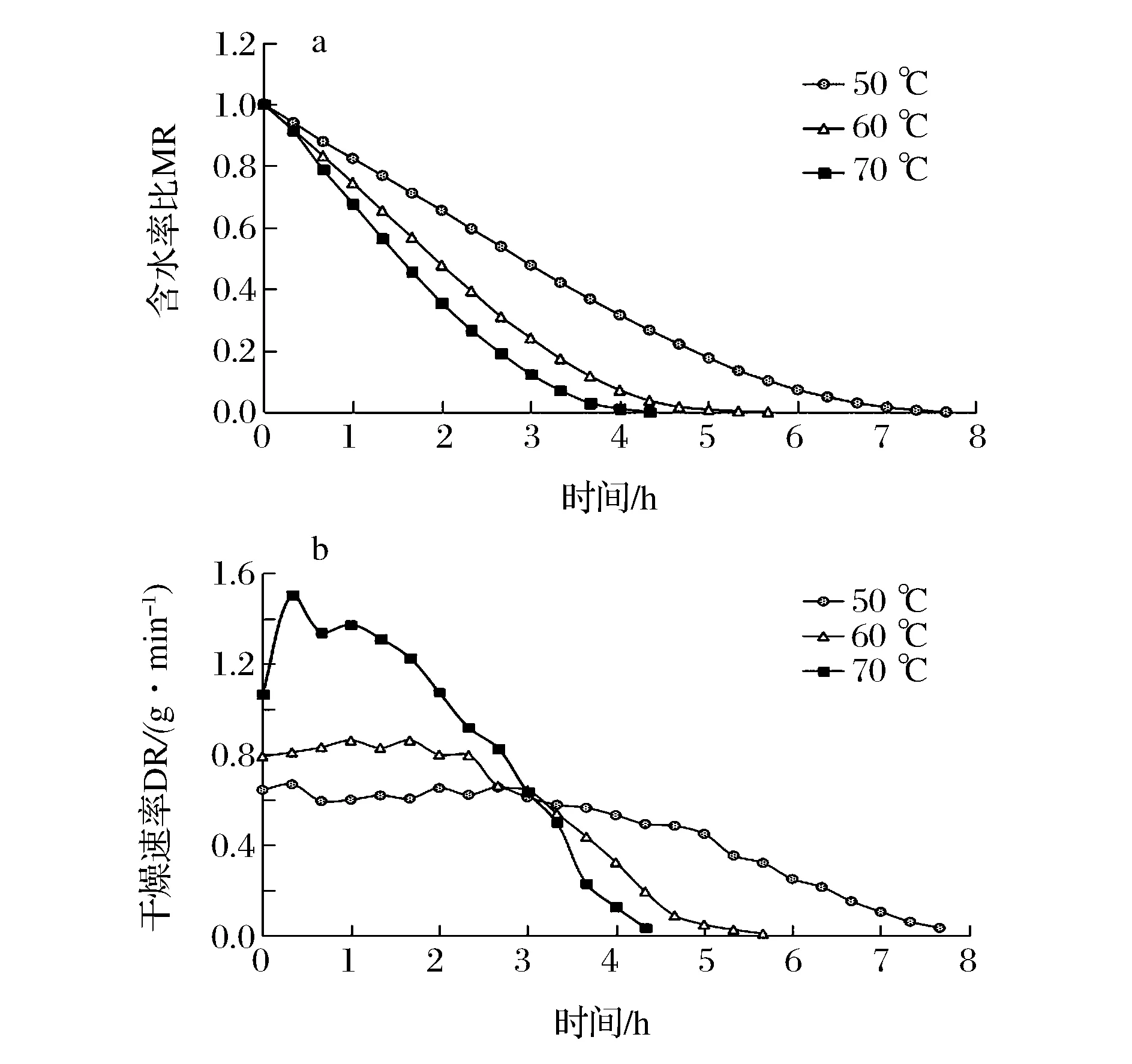
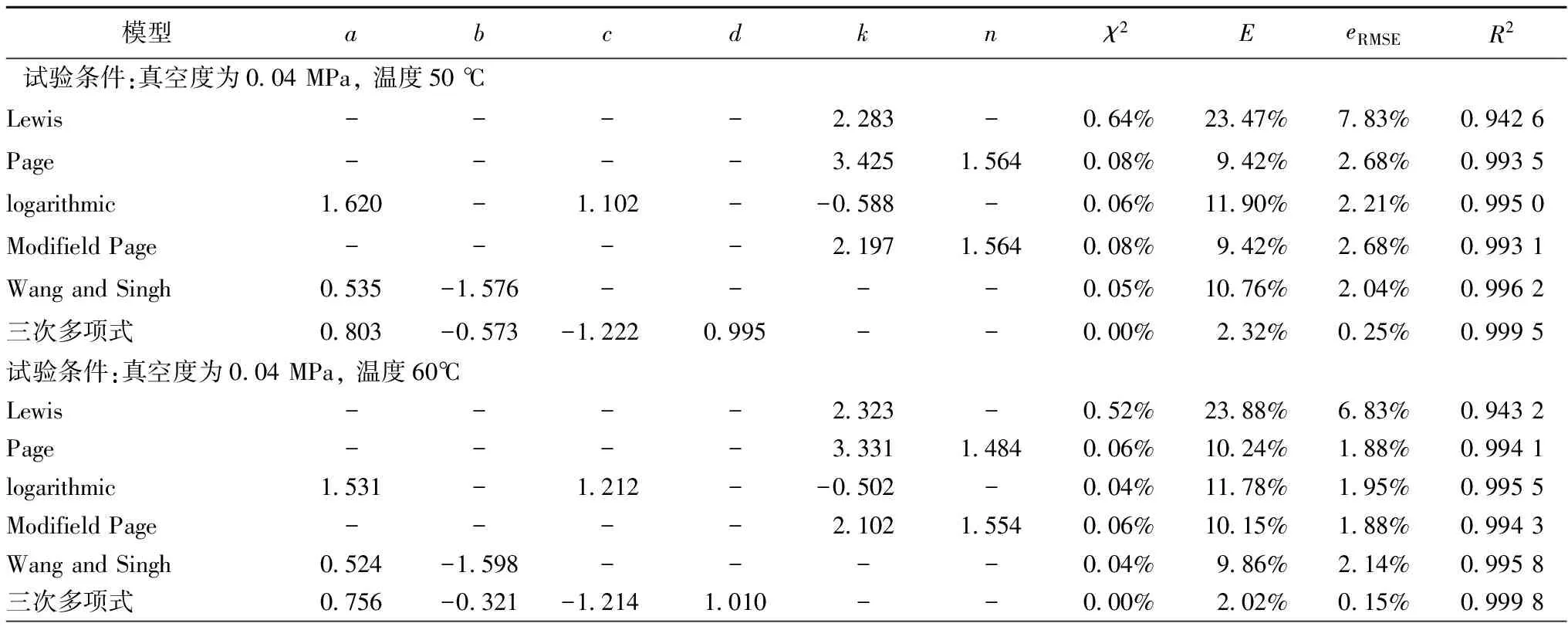
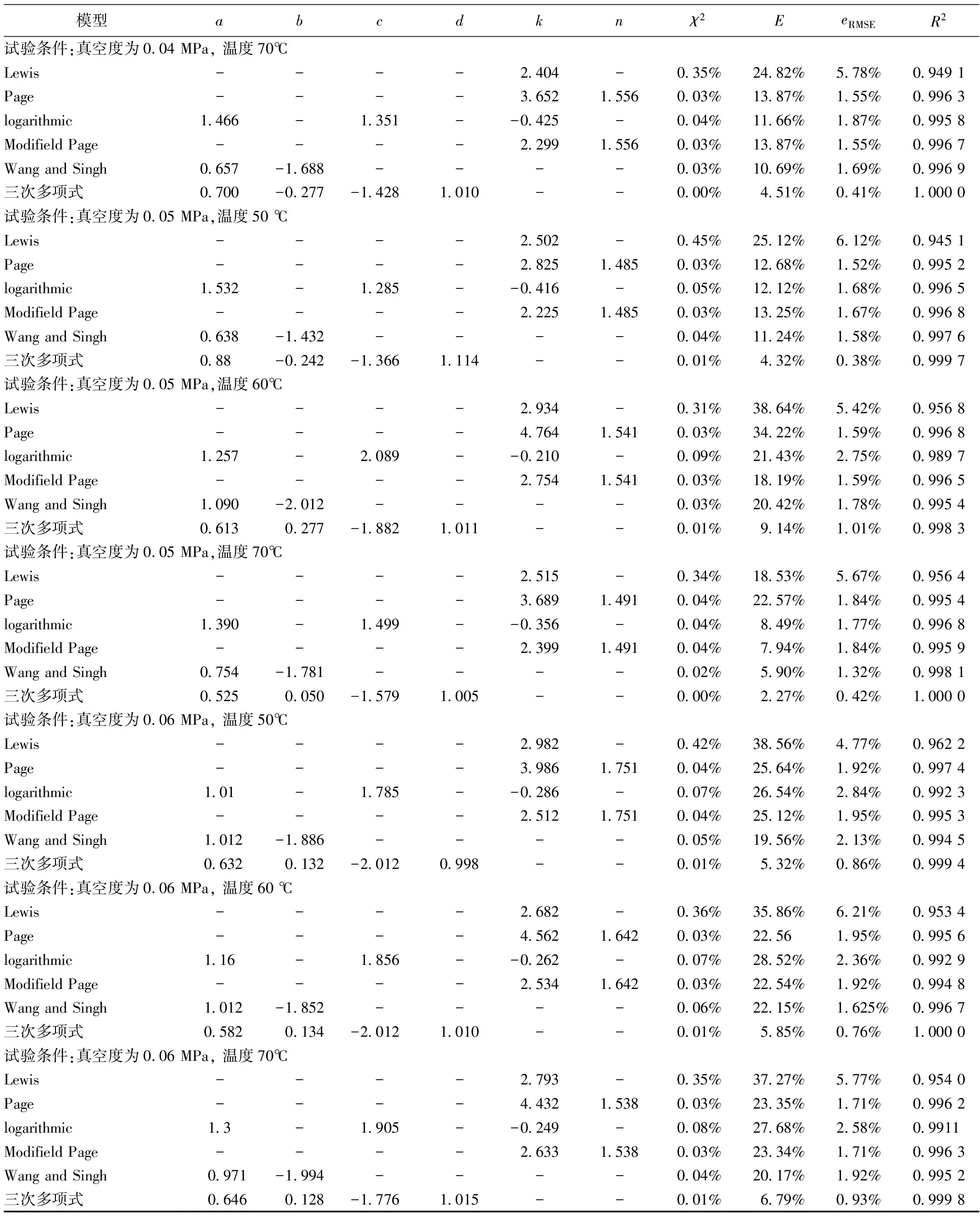
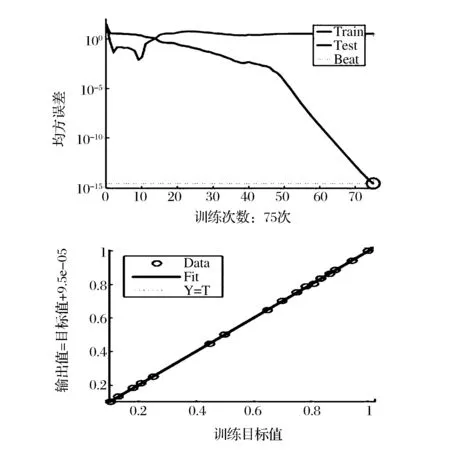
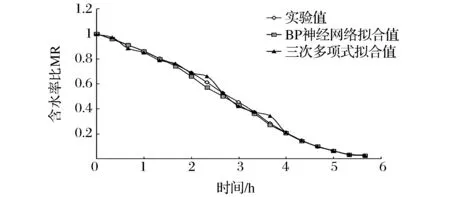
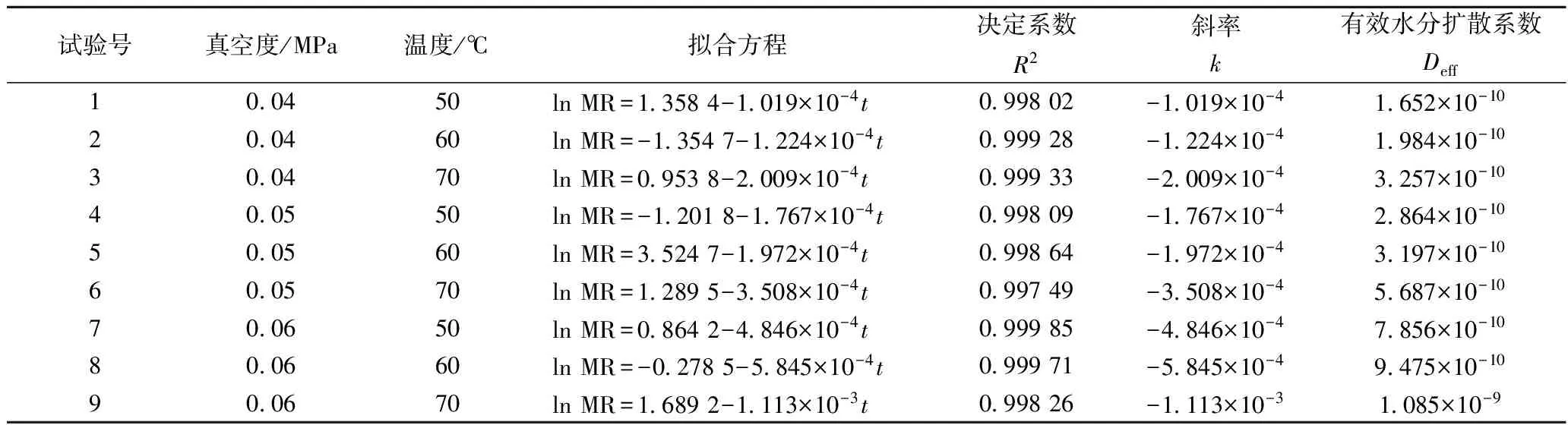
在本文中，a=3,b=1。则依据公式可得3

(4) 传递函数及算法

选择Tansig函数和Logsig函数作为隐含层的传递函数，线性函数Purelin作为输出层的传递函数。与传统BP算法相比，Levenberg-Marquardt算法梯度下降更快，在整个网络的收敛上能以很少的迭代次数达到误差要求[18]。因此采用Levenberg-Marquardt算法进行训练。

1.6数据预处理

由于本系统采用S型函数作为传递函数，当输入输出范围在区间[0,1]时，训练效果最佳，对各因素进行归一化处理：

xi=(x-xmin)/(xmax-xmin)

(11)

式中：xi为归一化处理后的数据；x为归一化处理前的数据xmax为原始数据组中最大值；xmin为原始数据组中最小值。

1.7统计方法

每组实验进行3次平行实验，取其平均值。运用SPSS20软件对6个经典模型进行拟合，采用MATLAB8.0对数据进行BP神经网络训练和拟合。

2 结果与分析

2.1真空度对干燥特性的影响

在干燥温度为70 ℃的条件下，分别设定干燥仓内真空度为0.04、0.05、0.06 MPa，考察真空度对魔芋干燥特性的影响。不同真空度条件下魔芋含水率比变化曲线以及干燥速率变化曲线如下图1所示。

图1 干燥温度为70 ℃时，不同真空度条件下魔芋含水率比MR和干燥速率DR随时间变化曲线Fig 1 Variation of moisture content and drying rate of konjac at different vacuum and a constant drying temperature at 70 ℃ with time

由图1-a可以看出，在温度相同的条件下，真空度越高，干燥过程中魔芋的水分比变化就越大，魔芋达到平衡含水率的时间就越短。其中，真空度在0.04、0.05、0.06 MPa条件下，干燥样品达到平衡含水率时间分别为243、262、280 min；一方面是由于在不同真空度下水的沸点不同，气压愈低，水的沸点愈低，较高的真空度加速了水分的汽化。另一方面在真空干燥过程中，魔芋内部及外部还存在着压力差，使得被汽化的水分子加速向真空空间移动。因此，真空度越高，越有利于水分在较低的温度下汽化。由图1-b可以看出：在不同真空度条件下，干燥速率达到最大值的时间均在30～45 min，真空度为0.04、0.05、0.06 MPa时干燥速率最大值分别为1.518%d.b/h、1.39%d.b/h和1.68%d.b/h。

2.2干燥温度对魔芋干燥特性的影响

在真空度为0.04 MPa的条件下，分别设定温度为50、60、70 ℃，考察干燥温度对魔芋干燥特性的影响。不同温度条件下魔芋含水率比以及干燥速率曲线如图2所示。

图2 真空度为0.04 MPa时，不同真空度条件下魔芋含水率比MR和干燥速率DR随时间变化曲线Fig.2 Variation of moisture content and drying rate of konjac at different drying temperature and a constant vacuum of 0.04 MPa with time

由图2-a可得：温度越高，魔芋达到平衡含水率所需的时间越短，在50℃条件的干燥时间约是70 ℃条件下的1.71倍，干燥前期的干燥速率比干燥后期的干燥速率快；魔芋为含湿多孔介质，含湿多孔介质在对流对流干燥时，传热传质过程同时发生且相互耦合。温度越高，魔芋表面就能快速获得足够的热量从而促进自由水分的蒸发，而多余的潜热则由魔芋表面传向魔芋内部，促使内部液相蒸发。从图2-b中可以看出魔芋真空干燥过程中没有明显的恒速干燥期，当干燥发生30 min左右时达到最大干燥速率为1.58%d.b/h，干燥发生前180 min均为加速期，这是由于干燥初期脱水主要成分为魔芋球茎组织内的大量游离水。当干燥发生180 min时，水分从内部迁移到表面的速率小于从表面蒸发到空气中的速率，导致干燥速率减小，进入降速阶段。

2.3魔芋真空干燥数学模型

根据前人研究成果，常见的食品薄层干燥数学模型如表1所示。采用SPSS20软件，运用表1中6种数学模型分别对试验数据进行拟合，所有模型参数及评价指标(E、R2、χ2和eRMSE)均列于表2。结果表明：在9种试验条件下，三次多项式模型的决定系数R2值均大于0.998 3，高于其他几种模型的决定系数值。平均相对误差E值都低于10%，最大值为9.14%，均小于其他五个模型的E值，其卡方χ2值均小于0.01%，也都高于其它几种模型的卡方值；均方根误差eRMSE值最大为1.01%，均低于其他5种模型的均方根误差值。由此可见，最适合魔芋真空干燥特性的数学模型是三次多项式模型。

表1 食品真空干燥数学模型

表2 数学模型相关参数及评价指标

续表2

模型abcdknχ2EeRMSER2试验条件：真空度为004MPa，温度70℃Lewis----2404-035%2482%578%09491Page----36521556003%1387%155%09963logarithmic1466-1351--0425-004%1166%187%09958ModifieldPage----22991556003%1387%155%09967WangandSingh0657-1688----003%1069%169%09969三次多项式0700-0277-14281010--000%451%041%10000试验条件：真空度为005MPa，温度50℃Lewis----2502-045%2512%612%09451Page----28251485003%1268%152%09952logarithmic1532-1285--0416-005%1212%168%09965ModifieldPage----22251485003%1325%167%09968WangandSingh0638-1432----004%1124%158%09976三次多项式088-0242-13661114--001%432%038%09997试验条件：真空度为005MPa，温度60℃Lewis----2934-031%3864%542%09568Page----47641541003%3422%159%09968logarithmic1257-2089--0210-009%2143%275%09897ModifieldPage----27541541003%1819%159%09965WangandSingh1090-2012----003%2042%178%09954三次多项式06130277-18821011--001%914%101%09983试验条件：真空度为005MPa，温度70℃Lewis----2515-034%1853%567%09564Page----36891491004%2257%184%09954logarithmic1390-1499--0356-004%849%177%09968ModifieldPage----23991491004%794%184%09959WangandSingh0754-1781----002%590%132%09981三次多项式05250050-15791005--000%227%042%10000试验条件：真空度为006MPa，温度50℃Lewis----2982-042%3856%477%09622Page----39861751004%2564%192%09974logarithmic101-1785--0286-007%2654%284%09923ModifieldPage----25121751004%2512%195%09953WangandSingh1012-1886----005%1956%213%09945三次多项式06320132-20120998--001%532%086%09994试验条件：真空度为006MPa，温度60℃Lewis----2682-036%3586%621%09534Page----45621642003%2256195%09956logarithmic116-1856--0262-007%2852%236%09929ModifieldPage----25341642003%2254%192%09948WangandSingh1012-1852----006%2215%1625%09967三次多项式05820134-20121010--001%585%076%10000试验条件：真空度为006MPa，温度70℃Lewis----2793-035%3727%577%09540Page----44321538003%2335%171%09962logarithmic13-1905--0249-008%2768%258%09911ModifieldPage----26331538003%2334%171%09963WangandSingh0971-1994----004%2017%192%09952三次多项式06460128-17761015--001%679%093%09998

2.4BP神经网络预测模型

2.4.1 隐含层节点数的选择

由式(10)所初步设置的隐含层节点通过BP神经网络工具箱进行训练拟合，训练拟合结果见表3。

表3 不同隐含层节点训练结果Table 3 The training results based on variationalhidden-layer nodes

由表3可知：当隐含层节点数为10时，训练样本的均方误差最小为2.521 08e-2，说明当节点数为10时训练效果最好，因此选取隐含层节点数为10构造神经网络进行训练，训练结果如图3所示。从图中可以看出，经过75次训练，停止误差平方和达到2.640 5e-15，此时模型R值为0.999 98，说明此时模型拟合度较高，具有较高的可靠性。

图3 10个隐含层节点的神经网络训练图Fig.3 The training figure of neural network based on 10 hidden-layer nodes

此时网络权矩阵为：

W{2,1}=[0.396 04 0.187 66 -0.273 57 -0.954 5 -0.783 97 -0.774 05 0.691 29 0.634 23 1.092 9]

b{1}=[2.889 2 -2.112 8 1.240 9 -0.944 59 -0.944 59 0.625 39 -2.274 4 -2.192 6 2.607 1]

b{2}=[0.357 37]

2.5三次多项式模型和BP神经网络模型的检验

追加一组工艺参数条件为：真空度为0.55 MPa，干燥温度为55 ℃的实验对三次多项式模型和BP神经网络模型进行检验。在此条件下，三次多项式模型为：MR=0.982t3-0.528t2-1.521t+1.125，根据方程计算出拟合值，此时三次多项式模型平均相对误差E值为6.86%。将数该组实验数据通过已训练好的神经网络模型进行拟合，结果表明BP神经网络模型平均误差为1.32%。魔芋样品含水率比MR的实验值、三次多项式模型拟合值和BP神经网络拟合值对比如图4所示。从图中可以看出BP神经网络模型拟合曲线与实际值几乎完全吻合，拟合效果相对更好。综上所述，BP神经网络模型为魔芋真空干燥特性的最佳模型。

图4 三次多项式模型和BP神经网络模型的检验曲线Fig.4 Curves of testing results for Cubic Polynomial Model and BP neural network

2.6有效水分扩散系数和活化能

根据式(3)将9组实验数据进行线性拟合，得到拟合方程的斜率k，根据式(4)计算魔芋真空干燥的有效水分扩散系数Deff，不同干燥条件下魔芋的有效水分扩散系数如表4所示。从表中可以看出，在温度相同的情况下，真空度越高，Deff值越大，这主要是由于较高的真空度有利于魔芋水分的汽化，且魔芋内外部之间存在压强差同真空度成正比，真空度越内外部压强差越大，被汽化的水分子向空间迁移速度越快。相同真空度条件下，魔芋有效水分扩散系数Deff值随温度的升高而增加，随着温度的升高，热量传输速度加快，热量从介质外环境传递至魔芋表面的速度加快，外界向魔芋表面传递的热量用于蒸发消耗的潜热有剩余，使得介质温度升高促使液相蒸发加快，因此温度越高魔芋有效水分扩散系数Deff值越大。在真空度为0.04、0.05、0.06 MPa和温度为50、60、70 ℃条件下，魔芋有效水分扩散系数值在1.652×10-10～1.085×10-9，此结果与MADAMBA等[24]报道的食品物料干燥过程中测得的有效扩散系数范围10-9～10-11十分接近，证明实验结果可靠性较高。

将式(5)取对数可得：lnDeff=lnD0-Ea/(RTa),将lnDeff和 1/Ta的曲线进行线性拟合，根据拟合直线的斜率-Ea/R计算出魔芋真空干燥平均活化能Ea值为29.86 kJ/mol。表明魔芋真空干燥过程中，样品蒸发1 mol水时所需要的启动能量为28.96 kJ，其平均干燥活化能在同类型食品干燥中相对较小，代表着魔芋干燥较为容易，利于推广。

表4 不同条件下魔芋有效水分扩散系数

3 结论

(1) 同样条件下，魔芋真空干燥到达安全含水率时间分别与真空度和温度成反比，真空度、温度越高，到达安全含水率时间越短。魔芋真空干燥过程是典型的水分扩散降速过程，没有明显的恒速干燥阶段，结果与吴绍峰等[25]的魔芋热风干燥结论基本吻合。

(2) 将试验数据用6种经典数学模型进行非线性拟合，将平均相对误差E、决定系数R2、卡方χ2和标准误差eRMSE作为评价标准对6种经典模型进行比较，结果表明最适合描述魔芋真空干燥过程的模型是三次多项式模型其平均相对误差为6.86%，将其与BP神经网络模型进行比较得到魔芋真空干燥最佳模型为BP神经网络模型。其平均相对误差E为1.32%。

(3) 对试验数据进行线性化处理，得到魔芋有效水分扩散系Deff值在1.652×10-10～1.085×10-9，此结果与MADAMBA等报道的食品物料干燥过程中测得的有效扩散系数范围10-9～10-11十分接近，证明实验结果可靠性较高。魔芋真空干燥平均活化能Ea值为28.96 kJ/mol。

[1] 刘佩瑛.魔芋学[M].北京:中国农业出版社,2004:21-22.

[2] 张盛林.魔芋栽培与加工技术[M].北京:中国农业出版社,2005:18-20.

[3] 牛义,张盛林,王志敏,等.中国魔芋资源的研究与利用[J].西南农业大学学报(自然科学版),2005(5):69-73.

[4] 张诚博. 魔芋葡甘聚糖生物复配膜的研究及其在芒果保鲜中的应用[D].福州：福建农林大学,2010：36-38.

[5] 刁英,滕彩珠,吴金平，等. 魔芋的研究进展[J]. 安徽农学通报,2006,12(6):137-139.

[6] 李静,王志民,张忠，等.魔芋的应用价值与开发前景[J].西昌学院学报,2006,20(4):17-19.

[7] MASKAN M.Microwave/air and microwave finish drying of banana[J].Journal of Food Engineering,2000,44(2):71-78．

[8] ORAK H H, AKTAS T, YAGAR H, et a1.Effects of hot air and freeze drying methods on antioxidant activity, colour and some nutritional characteristics of strawberry tree (ArbutusunedoL.) fruit[J]．Food Science and Technology International,2012,18(4):391-402.

[9] TAKAHIRO O,SHOJI K,SHINATARO O,et al. Impacts of hot air and vacuum drying on the quality attributes of kiwifruit slices[J].Journal of Food Engineering,2014,125:51-58.

[10] VISHAL K, MANISH K, SANJAY K.热烫温度和时间对魔芋片干燥动力学和品质的影响(摘选)[J]. 农业工程, 2012,2(4):72-75.

[11] ChAN C, D S.JAYAS. Dynamic equilibrium moisture content for grain drying[J].Canadian Agricultureal Engineering,1998, 40(4):299-303.

[12] SADOWSKA J.Drying conditions andprocessability of dried rapeseed[J]. Journal of Science of Food and Agriculture, 1996,72(2):257-262.

[13] 冯亚运,催田田,张宝善，等. 魔芋气体射流冲击干燥特性及干燥模型[J].陕西师范大学学报(自然科学版), 2016,44(1):118-124.

[14] 叶维, 李保国.魔芋热泵干燥特性及数学模型的研究[J]. 食品与发酵科技, 2015,51(5):32-36.

[15] 和智坤, 赵改红, 李梦婷,等. 魔芋葡甘露寡糖的干燥加热硒酸化及其产物的抗氧化性[J]. 食品科学,2013,34(5):5-9.

[16] FALADE K O,ABBO E S.Air-drying and rehydration characteristics of date palm (PhoenixdactyliferaL.) fruits[J].Journal of Food Engineering,2007,79(2):724-730．

[17] WANG Zheng-fu,SUN Jun-hong,LIAO Xiao-jun,et al.Mathematical modeling on hot air drying of thin layer apple pomace[J].Food Research International,2007,40(1):39-46.

[18] 郭树国,李成华,王丽艳. 基于正交设计与BP网络优化人参真空冷冻干燥工艺参数[J].食品工业科技,2011，32(11):26-29.

[19] BRUCE D M.Exposed-layer barley drying，three models fitted to new data up to 150℃[J].Journal of Agricultural Engineering Research,1985,32(4): 337-347.

[20] PAGR G E.Factors influencing the maximum rates of air drying shelled corn in thin layers[D]. Purdue USA: Purdue University, 1949:138-142.

[21] TOGRUL I T,PEHLIVAN D.Mathematical modeling of solar drying of apricots in thin layers[J]. Journal of Food Engineering,2002,55(3):209-216.

[22] DIAMANTE L M,MUNRO P A.Mathematical modeling of hot air drying of sweet potato slice[J]. International Journal of Food Science and Technology,1991,26(1):99-109.

[23] BALASUBR AMANIAN S,SHAMA R,GUPTA R K.Validation of drying models and rehydration characteristics of betel(PiperbetelL.) leaves[J]. J·Food Sci·Technol,2011,48(6):685-691.

[24] MADAMBA P S,DRISCOLL R H,BUCKLE K A.Thin-layer drying characteristics of garlic slices[J]. Journal of Food Engineering, 1996,29(1):75-97.

[25] 吴绍峰,邱兵涛,彭桂兰.魔芋薄层干燥试验及数学模型的建立[J].中国粮油学报,2016,31(8):105-110.

Vacuumdryingcharacteristicsandmodelingofkineticsforkonjac

LI Bin,PENG Gui-lan*,WU Shao-feng,LUO Chuan-wei, QIU Guang-ying,YANG Ling

(College of Engineering and Technology, Southwest University,Chongqing 400715,China)

The vacuum drying technology was adopted to dry konjac slices to shorten the drying time for konjac large-scale operation. The initial moisture content of konjac is approximately 80%-85%, and this has to be reduced to below 15% for its long term storage. Drying characteristics of konjac slices, the effective moisture diffusion coefficient and the activation energy were investigated under varying conditions of drying temperature(50,60 and 70 ℃) and vacuum degrees (0.04,0.05 and 0.06 MPa). Different drying models were compared by the value ofE,R2,χ2andeRMSE. The best model was then compared with BP neural network model. The results showed that BP neural network was the best and E value of the network was 1.32%. The drying process of konjac is a controlled internal water diffusion and reduced dying process. The effective moisture diffusion coefficientDeffand the activation energyEawere calculated under different drying conditions. The results showed thatDeffis proportional to the vacuum and drying temperature, the average value ofEawas 28.96 kJ /mol.

konjac; drying;model; vacuum drying; dynamic

10.13995/j.cnki.11-1802/ts.013613

硕士研究生(彭桂兰教授为通讯作者,E-mail:pgl602@163.com)。

国家自然科学基金项目(31301575)

2016-12-13，改回日期：2017-01-17