基于刚-柔耦合模型的高速机车齿轮传动系统断齿故障仿真分析

, , ,

(1.石家庄铁道大学 机械工程学院，河北 石家庄 050043；2.石家庄铁道大学 土木工程学院，河北 石家庄 050043)

基于刚-柔耦合模型的高速机车齿轮传动系统断齿故障仿真分析

王贞云1,刘永强1,廖英英2,石鹏飞1

(1.石家庄铁道大学 机械工程学院，河北 石家庄 050043；2.石家庄铁道大学 土木工程学院，河北 石家庄 050043)

用三维建模软件SOLIDWORKS对DF4B型机车走行部传动系统进行建模，并利用有限元软件ANSYS对故障齿轮进行柔性建模，再将三维模型导入动力学仿真软件ADAMS中，建立刚-柔耦合模型并进行仿真，最后分析了不同测点处的振动仿真结果。结果表明：通过对不同故障齿轮的振动信号进行频谱分析可准确的判断出故障的发生频率及故障的严重程度。通过对同一故障的不同测点进行分析可知振动信号的传递性，从而为状态监测中传感器的布置提供了理论依据。

机车齿轮系统；断齿故障；刚-柔耦合模型；动力学仿真

0 引言

随着近年来我国经济的快速发展，我国的铁路事业得到了长足的进步，近10万km的铁路总里程位居亚洲首位，“四纵四横”高速铁路系统初步成形，“八小时城市圈”计划方兴未艾，大秦线重载铁路技术居世界前列。但是在铁路系统运营中也出现了各种各样的问题，在形形色色的问题中，机车故障无疑是铁路技术人员无法回避的麻烦。而在机车故障中，传动系统、齿轮箱故障是比较常见的故障，其中断齿故障又占到了齿轮箱故障的60%[1]，所以对于齿轮系统断齿故障的研究是非常有意义的。

国内外对于齿轮故障的研究方法有很多，目前对齿轮故障信号的检测手段主要是振动检测方法[1-4]，因为齿轮发生故障时，传动系统的振动频率和振幅会有明显的变化，易于监测。例如沈阳铁路局的JL-601A机车走行部检测系统就是对轮对、齿轮轴承的振动信号(主要是时域方法)进行分析以检测故障[5]。又如JK00430A铁路列车轴承齿轮故障诊断装置，也是分析轴承、齿轮的振动信号(主要是频域方法)，此装置采用共振解调技术[6-8]，可以辨别干扰噪音中的微小故障。此外，声发射技术也是目前较为精确、可靠的实时监测技术。

对于齿轮故障诊断的方法有很多，但是对于如何准确的采集齿轮箱中振动信号以及振动信号如何传递的研究比较少，针对此问题提出了基于刚-柔耦合模型的高速机车齿轮传动系统断齿故障仿真分析。首先利用三维建模软件SOLIDWORKS对DF4B型机车走行部传动系统进行建模，利用有限元软件ANSYS对故障齿轮进行柔性建模，再将三维模型导入动力学仿真软件ADAMS中，建立刚-柔耦合模型并进行仿真，通过建立刚柔耦合模型研究了如何在齿轮箱上布置传感器能准确的采集故障信号，并且对同一故障的不同测点进行分析可知振动信号的传递性，从而为状态监测中传感器的布置提供了理论依据。

1 齿轮传动系统模型的建立

图1 装配体

选择东风4B内燃机车(DF4B)的传动系统作为断齿故障的研究对象，模型由轮对、车轴、啮合齿轮、齿轮箱、电机、电机输出轴、防滑垫圈、轴承、齿轮等组成。传动系统中大、小齿轮的模数为12 mm，分度圆压力角20°，齿厚140 mm。大齿轮的齿数为63，分度圆直径为756 mm。小齿轮齿数为14，分度圆直径为168 mm。使用SOLIDWORKS[10]三维建模软件进行建模，各零部件的模型建好后，需要根据各部件间的配合关系进行装配。装配体的模型在ADAMS[11]中也需要用到，所以装配过程中要以相互间正确的配合关系进行装配。完成的装配体如图1所示。

由SOLIDWORKS输出parasolid文件(.x_t文件)，再将其导入ANSYS[12]。通过ANSYS软件对导入的模型划分有限元单元，然后建立刚性区域，最后输出小齿轮的中性文件(mnf文件，即柔性体文件)，再导入ADAMS中，从而实现对柔性体的仿真。在ANSYS中柔性体的模型的参数(杨氏模量、泊松比、密度等)要做到尽量和实际情况一致，因为这些参数的精确与否直接影响了ADAMS中的仿真精度。

2 基于ADAMS的齿轮传动系统刚柔耦合动力学仿真

断齿故障通常都发生在小齿轮上，所以只需将小齿轮进行柔性体替换即可。虽然ADAMS本身的flex插件可以生成柔性体，但其生成的柔性体精确度低、易丢失重要信息，所以采用ANSYS生成中性文件，再替换ADAMS中的刚体，这样建模比较精确。ANSYS建立的小齿轮的柔性模型如图2所示。用柔性体齿轮替换完刚体之后的刚柔耦合模型如图3所示。

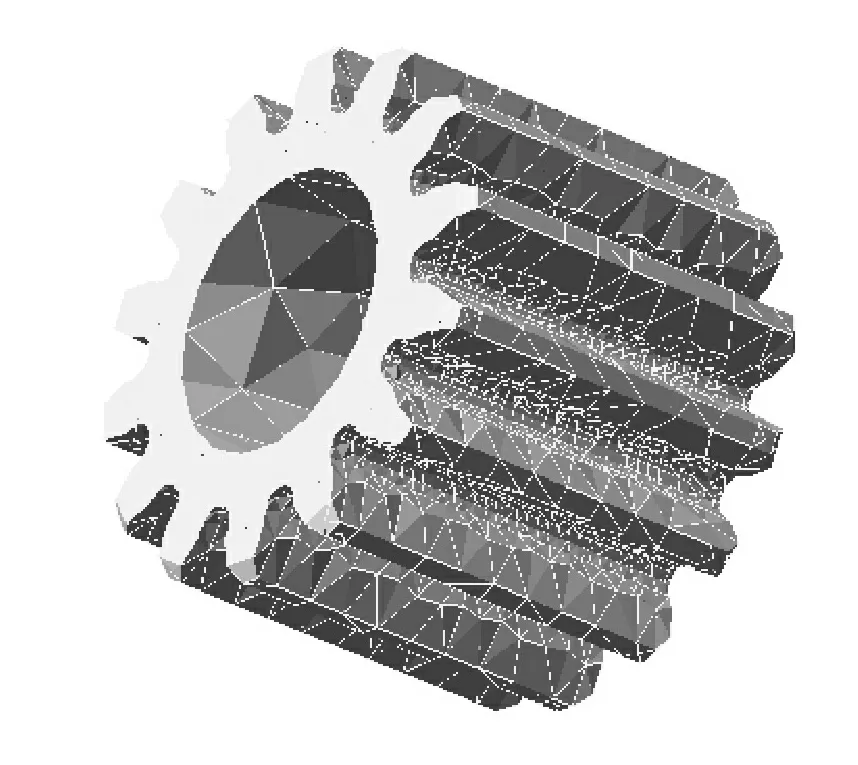
图2 小齿轮的柔性体模型

图3 刚柔耦合模型

一共建立4个刚柔耦合模型，与4个刚体小齿轮模型相对应，分别为：

(1)完整小齿轮刚柔耦合模型；

图4 插入测量点

(2)故障代号A(较轻断齿故障)小齿轮刚柔耦合模型；

(3)故障代号B(中等断齿故障)小齿轮刚柔耦合模型；

(4)故障代号C(严重断齿故障)小齿轮刚柔耦合模型。

为测量齿轮箱的振动加速度，以及振动加速度的传递性，需要在齿轮箱上插入若干个测量点，点的分布尽量均匀。从齿轮箱电机输出轴附近到车轴上方均匀插入了5个测量点，测量齿轮箱上箱体表面在这些位置的竖直方向上的振动加速度。齿轮箱插入测量点如图4所示。

3 振动信号时、频域分析及振动的传递性

3.1对振动信号进行时、频域分析

采用了故障诊断时域特征量中的峰值、平均幅值、均方根幅值、方根幅值4种指标对信号进行评测。

经Matlab[13]计算后列出4个模型在测点1处振动加速度的时域指标见表1。

表1 不同故障测点1处时域特征比较

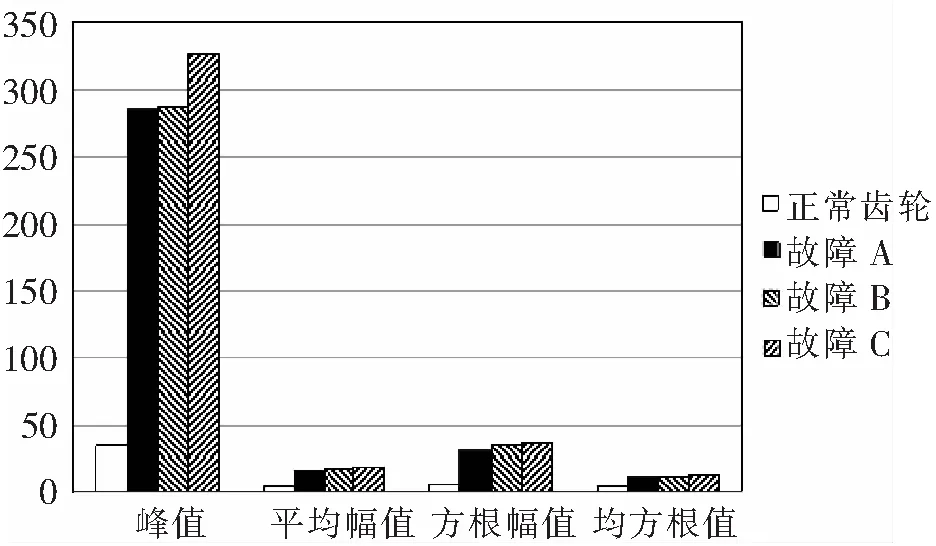
图5 不同故障测点1处时域特征柱状图比较

为了更直观的表现不同故障时域特征的区别，由表1中的数据绘制柱状图，如图5所示。

由图5可以直观的看出，完整齿轮传动系统4个时域特征的幅值远远小于有断齿故障传动系统的时域特征幅值。对4种模型在齿轮箱测点1的振动加速度的信号分别进行离散傅里叶变换，对比得到的频域特征，以找到断齿故障的故障特征频率。

对4组数据进行频谱分析后得到的频谱图如图6所示。

图6 不同故障齿轮测点1频谱图

由图6可以清晰的看出，完整齿轮传动系统齿轮箱振动信号频谱图中各频率幅值均较低。这说明完整齿轮传动系统啮合平稳，没有振动能量较高的频率，也间接的反映了此传动系统没有故障。

与完整齿轮的振动信号相比，A、B、C 3个故障齿轮传动系统振动信号的频谱图幅值相对较高，并且幅值最大值均出现在10.7 Hz附近，由此可以认为断齿故障传动系统的故障频率在10.7 Hz附近。并且在故障频率处幅值随着故障严重程度的增加而增大，这是因为断齿故障越严重，在断齿处啮合时的冲击能量就越大，所以相应的在故障频率处的幅值就会增大(在此频率处的能量增大)。

3.2振动的传递性讨论

首先对故障C(严重断齿故障)5个不同的测量点的时域特征进行分析。经Matlab计算后列出5个不同测量点处振动加速度的时域指标见表2。

表2 不同测点时域特征比较

为了更直观的表达，现画出平均幅值与均方根幅值的折线图，如图7。

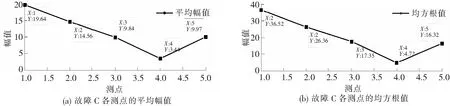
图7 故障C齿轮的平均幅值与均方根幅值

从图7可以看出测点1到测点4，时域特征大小随着与故障点距离的增加而减小，初步证明了振动的传递性。但是，无论是从图中还是表中都可以看出测点5处的时域特征值大于测点4处的数值。为什么会出现这种情况，为研究这个问题，通过分析正常齿轮模型所得到各测点的时域特征，见表3和折线图8。

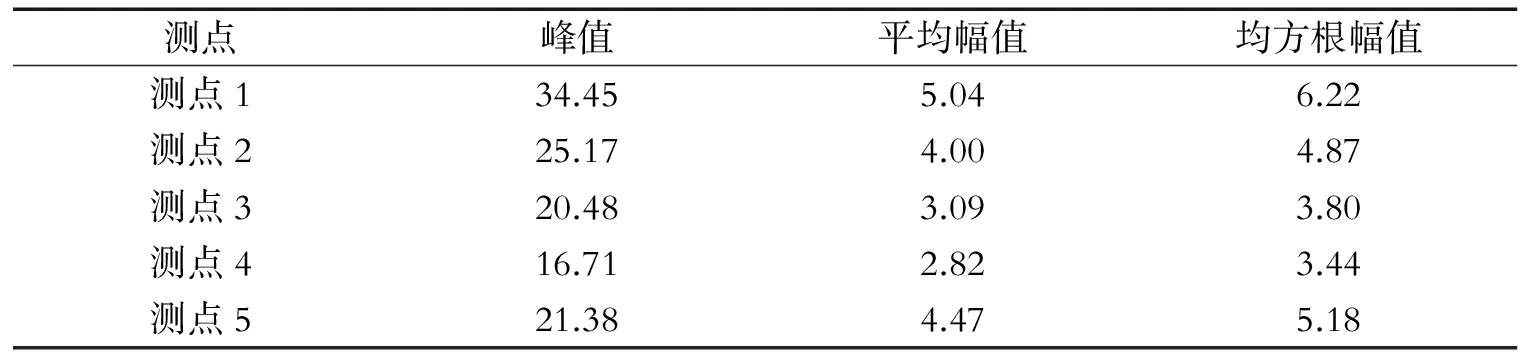
表3 正常齿轮模型

由图8可知，在完整齿轮传动模型中，测点5处的时域特征数值也大于测点4处的时域特征数值。对于出现这个问题作了猜测，可能是因为测点5的位置处于车轴的正上方，并且距离齿轮啮合点较远，所以测点5处的振动受车轴转动的影响较大，受啮合点冲击的影响较小，从而出现了测点5处的时域值大于测点4处的现象。

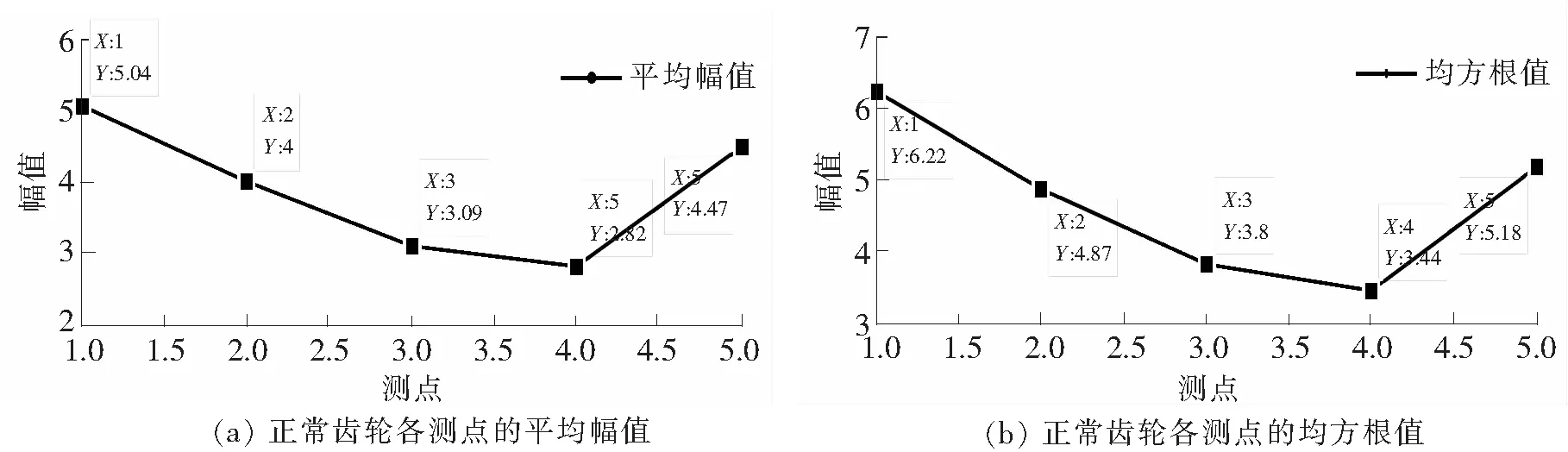
图8 正常齿轮的平均幅值与均方根幅值

对齿轮箱上箱体表面各个测点的时域特征的分析初步证明了振动的传递性，为了进一步验证测点5处的振动信号时域特征值大于4处的数值是因为车轴转动引起的，对故障C模型测点1到5信号的时域信号进行了频谱分析，如图9所示。

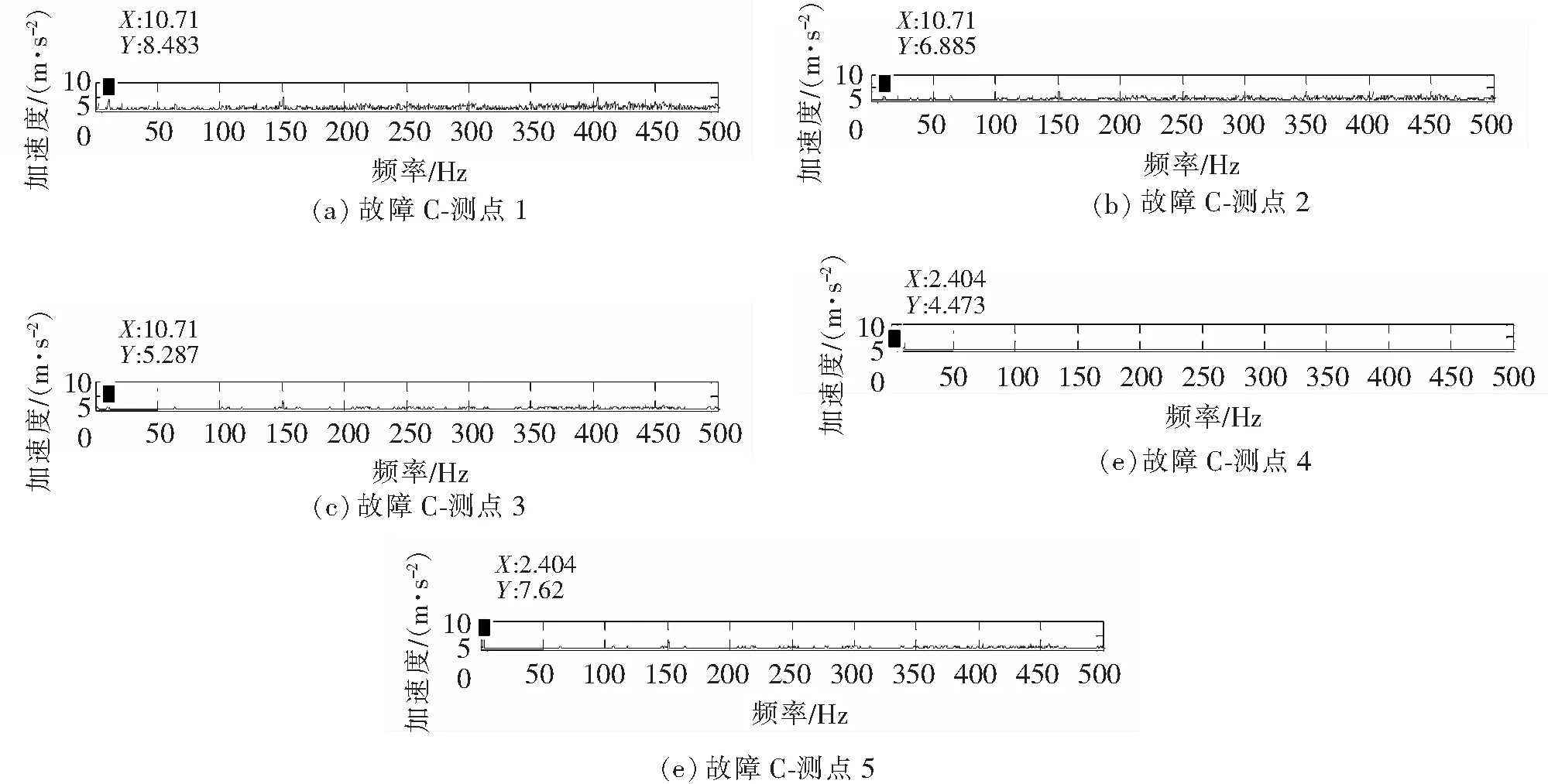
图9 故障C齿轮各点频谱图

由图9可知，测点1到测点4的信号频谱图在断齿故障的故障频率10.71 Hz处都有较大幅值，而测点5的信号频谱图却不具有此特征。这是因为测点5离发生齿轮故障的位置较远的缘故，这导致了测点5的振动信号中不包含任何有关齿轮断齿故障的信息。从测点1到测点4处的振动信号频谱图中，可以发现故障特征频率处的幅值是逐渐变小的，并且不止特征频率，在其余频率处的幅值也具有这个特征。幅值的大小代表着此处频率所具有能量的大小，也就是说测点1到测点4的振动能量是依次减少的，这也从侧面佐证了振动的传递性。

同时也会发现在测点4和测点5的振动信号频谱图在频率为2.404 Hz处幅值较高，在测点5处表现的尤为突出。而2.404 Hz与车轴的转频极为接近，也就是说测点4以及测点5的振动信号体现了一部分车轴转动的信息，解释了为什么测点5处比测点4的幅值大，并验证了猜测的正确性。

4 结论

通过Solidworks对齿轮传动系统进行建模，并在ADAMS中进行刚柔耦合动力学仿真，将采集的数据导入Matlab中进行分析，可得出以下结论：

(1)通过对不同故障齿轮的时域特征指标分析，可以判断出齿轮是否出现了故障及其故障严重程度，但不能知道故障具体发生在什么位置，再进行频谱分析后，可以准确判断出齿轮的故障发生在10.7 Hz处，并且也能够根据幅值的大小判断故障的严重程度。

(2)通过对故障C(严重断齿故障)齿轮及完整齿轮的不同测点的时域特征指标分析，可以验证振动信号的传递性。然后对故障C(严重断齿故障)齿轮的5个测点的频谱进一步分析可知，只有测点5在齿轮故障特征频率10.7 Hz处，没有突出幅值，说明测点5处不含有故障信息，而且测点4以及测点5的振动信号在2.404 Hz处有明显幅值，这两测点处体现出了一部分车轴转动的信息，为车轴、车轮以及大齿轮的状态监测布置传感器提供了理论依据。

[1]钱济国,吴淼. 齿轮故障的振动检测与分析[J]. 振动、测试与诊断,1990,10(1):36-41.

[2]Yin J, Wang W, Man Z, et al. Statistical modeling of gear vibration signals and its application to detecting and diagnosing gear faults[J]. Information Sciences An International Journal, 2014, 259(3):295-303.

[3]陈汉新,刘岑,杨诗琪. 检测与诊断齿轮裂纹故障的一种方法[J]. 武汉工程大学学报, 2014, 36(9):53-58.

[4]张丹,张战果,郭世红. 振动检测在卷取机齿轮故障诊断中的应用[J]. 武钢技术, 2015, 53(1):54-56.

[5]李欣.机车走行部牵引齿轮故障检测[J]. 铁道机车车辆, 2010, 30(6):95-96

[6]Wang W.Early detection of gear tooth cracking using the resonance demodulation technique[J]. Mechanical Systems & Signal Processing, 2001, 15(5):887-903.

[7]丁芳,高立新,崔玲丽,等.共振解调技术在设备故障诊断中的应用[J]. 机械设计与制造, 2007(11):178-179.

[8]Yu D, Yang Y, Cheng J. Application of time-frequency entropy method based on Hilbert-Huang transform to gear fault diagnosis[J]. Measurement,2007, 40(9/10):823-830.

[9]孙豪杰. JL-601机车走行部诊断系统的应用及改进[J]. 铁道机车车辆, 2004, 24(3):53-54.

[10]张红松,胡仁喜,路纯红.SOLIDWORKS 2011中文版标准教程[M].北京:科学出版社,2011.

[11]李增刚.ADAMS入门详解与实例[M].北京:国防工业出版社,2006.

[12]周宁.ANSYS机械工程应用实例[M].北京:中国水利水电出版社,2006.

[13]阮沈勇,王永利,桑群芳.MATLAB程序设计[M].北京:电子工业出版社,2003.

ModelingandSimulationofFlexibleBodyToothFractureFaultofGearTransmissionSystemofHighSpeedLocomotive

WangZhenyun1，LiuYongqiang1，LiaoYingying2，ShiPengfei1

(1.School of Mechanical Engineering， Shijiazhuang Tiedao University， Shijiazhuang 050043， China;2. School of Civil Engineering， Shijiazhuang Tiedao University， Shijiazhuang 050043， China)

The 3D model of transmission system is established by using SOLIDWORKS, and the flexible model of the fault gear is established by using ANSYS. Then the 3D model is imported into the dynamic simulation software ADAMS ,and the fault gear is changed by the flexible model. After the simulation, the results are imported into Matlab respectively. Results show that, based on spectrum analysis of different fault gear vibration signal, the fault occurrence frequency and severity of failure can be accurately judged. The transitivity of vibration signal can be known through analysis of different points of the same fault, which provides theoretical basis for the arrangement of sensors in condition monitoring.

tooth fault；flexible model；dynamic simulation；ADAMS

U270.1

： A

： 2095-0373(2017)03-0033-06

2016-05-25责任编辑:刘宪福

10.13319/j.cnki.sjztddxxbzrb.2017.03.07

国家自然科学基金(11227201;11202141; 11302137; 11472179;11572206;11372199)；河北省自然科学基金(A2013210013; A2015210005)；河北省教育厅项目(YQ2014028)

王贞云(1990-)，男，硕士研究生， 研究方向为机车轮对轴承故障诊断。E-mail:79948403@qq.com

刘永强(1983-)， 男，副教授，博士，研究方向为机车车辆故障诊断。E-mail:liuyq125@126.com 王贞云,刘永强,廖英英，等.基于刚-柔耦合模型的高速机车齿轮传动系统断齿故障仿真分析[J].石家庄铁道大学学报:自然科学版,2017,30(3):33-38.