钢筋混凝土梁在冲击波与破片联合作用下的动态响应分析

，

(1. 天津大学 建筑工程学院，天津 300072；2.滨海土木工程结构与安全教育部重点实验室(天津大学)，天津 300072)

钢筋混凝土梁在冲击波与破片联合作用下的动态响应分析

田力1,2，赵玲清1

(1. 天津大学 建筑工程学院，天津 300072；2.滨海土木工程结构与安全教育部重点实验室(天津大学)，天津 300072)

运用LS-DYNA软件，通过在炸药底部布置预制破片，模拟冲击波与破片对钢筋混凝土梁的复合作用。分析了冲击波单独作用、破片单独作用以及冲击波与破片复合作用下钢筋混凝土梁动态响应的不同。仿真结果表明：在冲击波与破片联合作用下，结构的毁伤程度远大于冲击波单独作用时。并且在冲击波与破片复合作用下，结构的动态响应大于在冲击波单独作用和破片单独作用下动态响应之和。破片群不仅产生局部破坏，还会将动能传递给钢筋混凝土梁，从而使结构产生整体破坏。

冲击波；破片；复合作用；钢筋混凝土梁

0 引言

武器爆炸会产生冲击波和大量的高速破片。这两种毁伤元都对结构产生破坏，但其毁伤机理不同。破片是对结构进行侵彻，削弱结构强度；冲击波主要是使结构产生变形、震塌。在近区爆炸时，冲击波和破片的联合作用对结构的破坏最大。早期，研究人员对于破片与冲击波的联合作用，主要是解耦，然后对破片和冲击波产生的破坏分别研究，并进行数值相加。近年来，人们认识到破片与冲击波对结构的毁伤破坏不是简单地叠加，而是具有增强效应。Leppänen通过实验和数值模拟分析了冲击波和破片对混凝土的复合作用，给出了其破坏模式，发现在冲击波和破片作用下，混凝土的破坏主要集中在受载区域。因此Leppänen认为冲击波和破片作用在设计阶段可以分开考虑[1]。Nyström利用AutoDYN软件并且采用单自由度方法研究了钢筋混凝土墙体在破片和冲击波复合作用下的动态响应，通过墙体中点联合作用时的位移大于分别作用时产生的位移之和，得出联合作用对结构破坏大于单一荷载产生破坏之和[2]。Hu等利用MPM方法对冲击波和破片协同作用下的混凝土墙进行了研究，得出带壳装药比不带壳装药产生的危害更大[3]。Kong等通过实验和数值分析研究了破片和冲击波对多层防护结构的联合毁伤作用，以及对带壳装药爆炸产生的破片速度的分布规律进行研究[4]。李伟等采用带壳装药模拟战斗部，并进行舱内爆炸试验，研究了冲击波与破片复合作用对结构破坏的影响，发现在破片密集作用区域，弹孔之间的边界由于冲击波作用撕裂并贯通[5]。

为研究钢筋混凝土梁在破片与冲击波联合作用下的动态响应，运用ANSYS/LSDYNA软件分别模拟了钢筋混凝土梁在破片群载荷、冲击波载荷及联合载荷作用下的变形及破坏。

1 数值模拟

1.1模型简介

运用LS-DYNA软件建立了钢筋混凝土简支梁的分离式模型(如图1所示)，模型由空气、炸药、破片和钢筋混凝土梁组成。空气、炸药、破片以及混凝土采用的是Solid164实体单元，钢筋采用的是Beam161梁单元。破片和钢筋混凝土梁采用Lagrange网格；炸药和空气采用Euler网格，使用多物质ALE算法。通过流固耦合的方法驱动破片飞散以及实现冲击波对钢筋混凝土梁的作用；破片对钢筋混凝土梁的侵蚀作用通过定义两者间的侵蚀接触实现。由于爆炸冲击荷载作用时间非常短，通常假定混凝土与钢筋之间粘结完好，因此建模时混凝土和钢筋之间的连接采用共节点方法。

混凝土保护层20 mm。钢筋混凝土梁的截面为200 mm×400 mm，跨度为3 m。梁箍筋配筋率为0.5%，纵筋直径为20 mm。单个破片质量为30 g，炸药底距钢筋混凝土梁500 mm。TNT炸药质量为3.2 kg，钢筋与混凝土单元为10 mm。

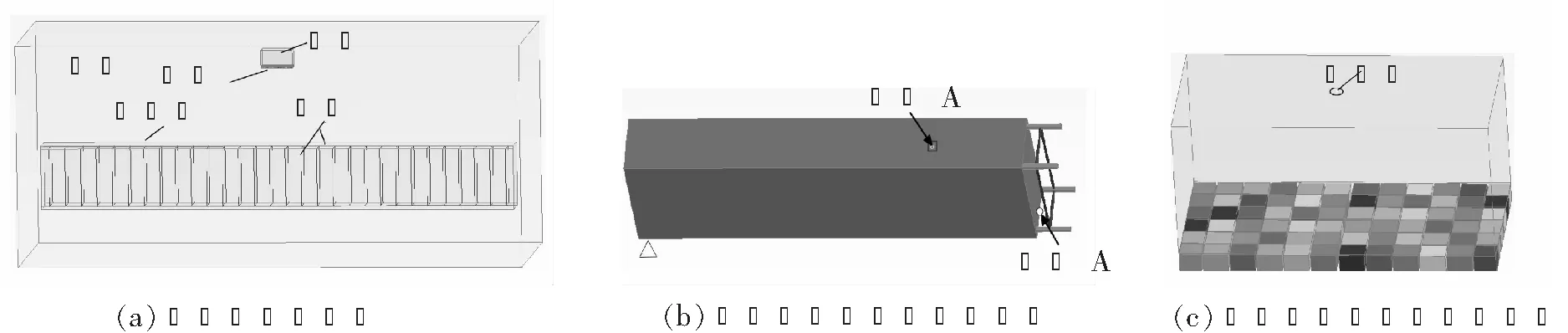
图1 有限元模型

1.2材料本构

破片采用刚体忽略其变形。

钢筋采用随动强化双线性弹塑性模型[6-7]，并通过Cowper-Symonds模型考虑应变率效应。钢筋应力表示为

(1)

钢筋采用的材料参数如表1所示。

表1 钢筋材料参数

混凝土采用*MAT_CONCRETE_DAMAGE_REL3(MAT72)[6-7]，该模型考虑了材料的应变率效应。混凝土材料的应变率效应通过混凝土强度增大系数DIF来表示[8]。混凝土强度增大系数DIF采用K&C模型。本文混凝土采用C30。

TNT炸药采用*MAT_HIGH_EXPLOSIVE_BURN[6-7]材料模型，采用JWL状态方程来描述。表达式如下

(2)

式中，P为爆轰压力；A,B,R1,R2,ω为材料常数；V为相对体积；E0为初始内能。

TNT参数如表2所示。

表2 TNT炸药的材料参数

表中：ρ0为质量密度；D为爆速；PCJ为(Chapman-Jouget) 压力。

空气采用*MAT_NULL[6-7]模型，以及采用LINEAR_POLYNOMIAL状态方程描述。表达式如下

(3)

式中，C0、C1、C2、C3、C4、C5、C6均是常数；E为单位体积内能。若μ<0，则C2μ2和C6μ2均设置为零，其中

(4)

式中，ρ为空气即时密度；ρ0为空气初始密度。

空气参数如表3所示。

表3 空气状态方程参数

2 计算结果与分析

2.1数值模型实验验证

运用Zhang[9]以及汪维[10]做的钢筋混凝土梁的实验来验证所建有限元模型的合理性。采用流固耦合方法和相同的材料模型验证参数的准确性。有限元模型见图2(a)，实验装置见图2(b)。该实验是对近爆下钢筋混凝土梁的动态响应进行了研究。实验中，TNT质量为0.51 kg，爆距为400 mm；钢筋混凝土梁的截面为100 mm×100 mm，跨度为1.1 m；箍筋纵筋直径都为6 mm，箍筋间距为60 mm；混凝土抗压强度40 MPa，钢筋强度为300 MPa；混凝土保护层厚度20 mm。建模时所采用的数据与实验一致，网格大小为10 mm。

图2 有限元模型及实验装置图[9]

文献[9]中测得梁的跨中最大位移是35 mm,梁的背面混凝土脱落区长度约为12 cm。

仿真结果中，在9 ms时梁跨中达到最大位移为31.6 mm，残余位移为26 mm，背面混凝土脱落区长度为11.2 mm。由仿真结果与实验对比可得，跨中最大位移两者相差9.7%，背面混凝土脱落区长度相差6.7%。误差来源可能是边界条件与实际有差异以及材料有偏差。数值模拟中梁跨中节点位移时程曲线如图3所示。从图4可以看出，有限元模拟的损伤结果与实验相近。

2.2破片飞散

采用单点起爆，破片在冲击波的驱动下向四周飞散，形成一定空间分布的破片群。距爆炸点最近的破片速度最大，随着距离增大，破片速度减小。这是由于稀疏波引起的。

在(0～0.4 ms)破片飞散形成破片群，破片飞散如图5所示。距爆心最近的破片的最大速度为1 478 m/s，而相距最远的破片的速度为790 m/s。破片的速度时程曲线如图6所示。同时由图7可知，距爆心距离越近，破片到达钢筋混凝土梁的时间越短，其中距离d为破片与爆心的水平距离。

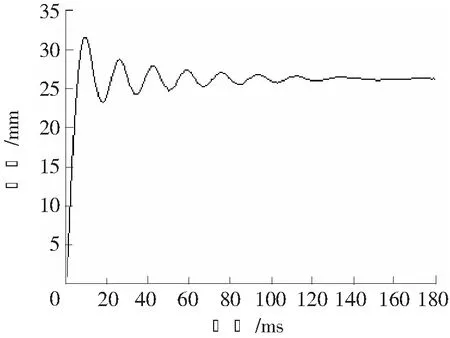
图3 梁跨中节点位移时程曲线

图4 梁塑性应变云图及实验损伤图

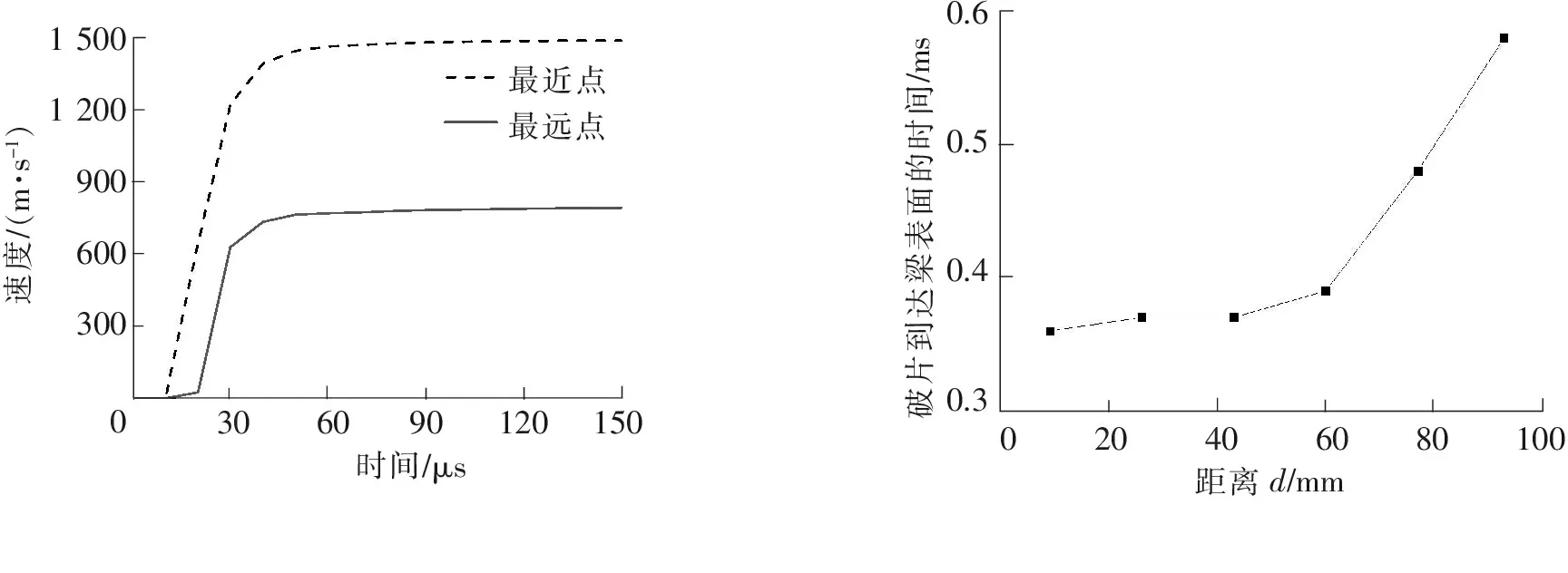
图6 破片速度时程曲线 图7 破片到达钢筋混凝土梁表面的时刻

2.3冲击波、破片单独作用以及联合作用结果对比分析

(1)通过使流体不与钢筋混凝土梁耦合，实现破片对混凝土梁的单独作用。先到达的破片使结构产生应力应变，这相当于给后到达的破片提供初始应力，从而使后到达的破片对结构产生的破坏更大。破片群对钢筋混凝土梁的破坏，先是破片群对结构的局部冲击与侵彻破坏。从而在梁的正面成坑，并且使部分钢筋切断，从而使钢筋混凝土梁的强度降低。并且在侵彻坑处产生应力集中，使钢筋混凝土梁抵抗整体变形能力大大降低。该过程分为两个阶段。

在第一阶段(0.4～0.8ms)破片群冲击钢筋混凝土梁，在梁正面侵彻成坑，由于梁中间部分破片密布，故会形成密集的侵彻坑。又由于应力波的叠加，各个弹坑相连接成一整片。在这个过程中，由于中间的破片速度大，因此先接触钢筋混凝土梁，两侧的破片后到达。中间部分的箍筋被切断，截面削弱，有效高度减小，强度降低，更易发生变形。损伤如图8所示。

在第二阶段(0.8～8ms)此时破片的速度降低到很小，对结构作用可忽略。钢筋混凝土梁吸收了破片群传递的动能后，继续产生整体变形，在6.35ms左右达到最大位移约8.2mm。这之后梁开始恢复变形。跨中节点A的位移时程曲线如图10所示。

从图8(g)可以看出，塑性区域集中在梁的中间部分，是由局部破坏效应和整体破坏效应共同引起。局部破坏先发生，后引起整体破坏，并且破片引起的破坏作用是不可忽略的。

(2)在t=0.2 ms时，破片早已达到最大速度，冲击波与破片的相互作用可忽略。此时删除破片，利用重启动，分析了钢筋混凝土梁在冲击波单独作用下的动态响应和破坏。由于冲击波在驱动破片的过程中，发生了反射以及绕流现象。因此冲击波到达钢筋混凝土梁时的峰值压力降低。在冲击波单独作用下，钢筋混凝土梁在4.4 ms左右挠度达到最大值1.4 mm，而后减小。由以上可知冲击波引起的破坏比破片引起的破坏小。梁跨中位移时程如图10所示。

(3)冲击波与破片复合作用下，由于冲击波的初始传播速度大于破片的初始速度，因此冲击波先到达，破片后到达。冲击波作用时间与破片作用时间有重叠，在该过程中冲击波与破片对钢筋混凝土梁的破坏进行了耦合。由图8与图9对比可以看出，在相同的时刻，联合作用下混凝土剥落更严重，钢筋变形更大。这是由于冲击波先作用，使结构处于一定的应力状态下，破片更易对结构进行侵彻，造成局部破坏。同时冲击波作用使局部破坏处产生应力集中，使结构产生更大的破坏。钢筋混凝土梁在破片与冲击波联合作用下的位移时程曲线如图10所示，在7.75 ms左右钢筋混凝土梁达到最大位移10.7 mm。由图10可知，钢筋混凝土梁在不同的载荷作用下，其产生最大响应的时间不同。在冲击波单独作用下，在4.4 ms时，结构响应最大；在破片单独作用下，在6.35 ms时，结构响应最大；在联合作用下，在7.75 ms时，结构响应最大。并且联合作用下的最大响应大于分别作用之和。由于产生最大响应的时间不同，因此不能进行简单的数值叠加。单元A在联合作用、破片单独作用以及冲击波单独作用下的应力如图11所示。单元A的位置见图1。由图11可知，在联合作用下，单元应力在0.55 ms达到最大值28.7 MPa；在破片单独作用下，单元应力在0.65 ms达到最大值24 MPa；在冲击波单独作用下,单元应力在4.5 ms达到最大值8 MPa。在0.55 ms时,破片单独作用时单元应力为9.6 MPa，冲击波单独作用单元应力为1.9 MPa。在此时刻，联合作用时的应力是破片单独作用时的2.5倍左右。这说明在此时刻，冲击波与破片作用进行了耦合，出现应力集中。

图8 破片作用下简支梁的塑性应变云图

图9 联合作用下简支梁的塑性应变云图

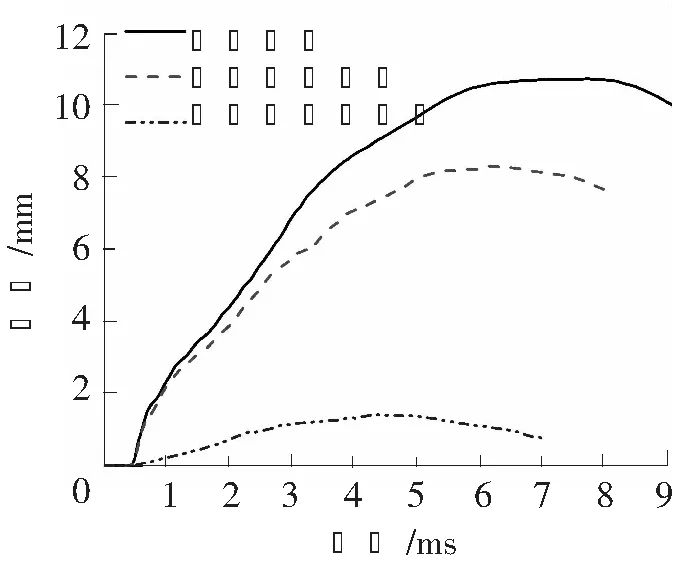
图10 梁在联合作用、破片、冲击波单独作用下跨中位移

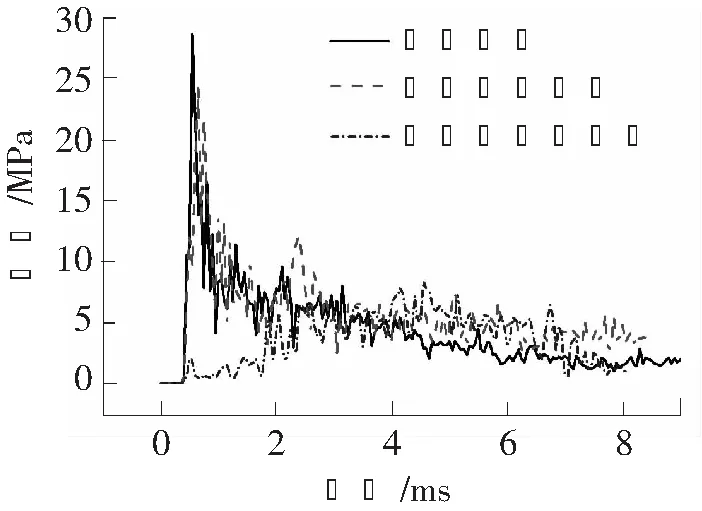
图11 梁在联合作用、破片、冲击波单独作用下单元A应力

3 结论

运用LS-DYNA软件，对破片和冲击波对钢筋混凝土梁的协同作用进行了数值分析。

得出以下结论：

(1) 通过冲击波的驱动，实现破片飞散并且距起爆点越近，破片获得的速度越大，相应的动能越大。中间破片速度大，对结构破坏严重。

(2) 破片群的破坏与单个破片不同，破片群不仅引起局部破坏，而且也引起整体响应。单个破片会使结构产生侵彻坑，而破片群会将侵彻坑连成一片，大大削弱结构的有效高度，降低结构的承载力。破片群的破坏力很大，应该考虑。

(3) 冲击波单独作用下，引起的动态响应很小，这是由于冲击波驱动破片飞散后，其中一部分能量变成了破片的动能，故冲击波作用于结构的能量减小。

(4) 冲击波与破片联合作用下，钢筋混凝土梁产生的位移大于单独作用之和。结构在破片单独作用、冲击波单独作用以及联合作用下产生最大位移的时间是不同的，因此不能简单地进行叠加。

[1] Joosef L. Experiments and numerical analyses of blast and fragment impacts on concrete [J]. Int J Impact Eng, 2005, 31: 843-860.

[2] Nyström U, Gylltoft K. Numerical studies of the combined effects of blast and fragment loading [J]. Int J Impact Eng, 2009, 36: 995-1005.

[3] Hu W, Chen Z. Model-based simulation of the synergistic effects of blast and fragmentation on a concrete wall using the MPM [J]. Int J Impact Eng, 2006, 32: 2066-2096.

[4] Kong X S, Wu W G,Li J, Chen P. Experimental and numerical investigation on a multi-layer protective structure under the synergistic effect of blast and fragment loading [J]. International Journal of Impact Engineering, 2014, 65: 146-162.

[5] 李伟,朱锡,梅志远,等.战斗部舱内爆炸对舱室结构毁伤的实验研究[J]. 舰船科学技术,2009,31(3): 34-37.

[6] Hallquist J O. LS-DYNA Theory Manual [M]. California: Livermore Software Technology Corporation, 2006: 273-277.

[7] Hallquist J O. LS-DYNA Keyword User’s Manual [M]. California: Livermore Software Technology Corporation, 2007: 1430-1432.

[8] Malvar L J, Ross C A. Review of strain rate effects for concrete in tension [J]. ACI Materials Journal, 1998, 96(5): 735-739.

[9] Zhang D. Experimental study on scaling of RC beams under close-in blast loading[J]. Engineering Failure Analysis, 2013, 33: 497-504.

[10] 汪维. 钢筋混凝土构件在爆炸荷载作用下的毁伤效应及评估方法研究[D].长沙:国防科技大学, 2012.

DynamicResponseoftheReinforcedConcreteBeamUnderBlastandFragmentLoading

TianLi1,2,ZhaoLingqing1

(1.School of Civil Engineering, Tianjin University, Tianjin 300072, China;2.Key Laboratory of Coast Civil Structure Safety(Tianjin University),Ministry of Education, Tianjin 300072, China)

In this thesis, the synergetic effects of blast wave and fragment on reinforced concrete beam are simulated by using LS-DYNA software by placing fragments at the bottom of the charge. Numerical simulation is used to analyze the different dynamic responses of different models. The dynamic responses of the reinforced concrete beam for blast loading, fragment loading and simultaneous loading are studied. The results show that the damage of the reinforced concrete beam subjected to simultaneous loading is severer than that subjected to blast loading alone. In addition, the response of the reinforced concrete beam under combined loading is bigger than if adding that under fragment and blast loading treated separately. Not only is local failure caused by fragment cluster, but integral damage is also caused by fragment cluster, which transfers the impulse to the structure.

blast wave;fragment;synergetic effects;reinforced concrete beam

TU375.1

： A

： 2095-0373(2017)03-0006-07

2017-03-26责任编辑:车轩玉

10.13319/j.cnki.sjztddxxbzrb.2017.03.02

国家自然科学基金(51178310,50678116)

田力(1970-),男,博士，副教授，主要从事工程结构抗爆、抗冲击理论的研究。E-mail:ltian@tju.edu.cn 田力，赵玲清.钢筋混凝土梁在冲击波与破片联合作用下的动态响应分析[J].石家庄铁道大学学报:自然科学版,2017,30(3):6-11.