基于八元数Cauchy积分公式的血管分割算法*

王晓婵，吴明珠，李兴民

(1. 南方医科大学 图书馆, 广东 广州 510515; 2. 广州商学院 计算机系, 广东 广州 511363;3. 华南师范大学 计算机学院, 广东 广州 510631)

基于八元数Cauchy积分公式的血管分割算法*

王晓婵1，吴明珠2，李兴民3

(1. 南方医科大学 图书馆, 广东 广州 510515; 2. 广州商学院 计算机系, 广东 广州 511363;3. 华南师范大学 计算机学院, 广东 广州 510631)

针对现有的血管分割方法会因图像中噪声的影响，而不能将断裂的血管部分分割出来，导致分割精细程度不够高的问题，提出一种新的基于八元数Cauchy积分公式的血管分割新算法。该方法首先根据血管走向构造合适的六维向量，提取出体数据中的每一个像素点六维方向上6个邻域点的像素值，并将其构造成一个八元函数。然后，构造一个封闭的立方体区域，将封闭立方体区域边界上 26 个点对应的八元函数的平均作为中心点的八元函数，并将其表示成种子点特征向量。最后，遍历图像数据，用种子点的特征向量与每一点的特征向量做乘积，通过判断内积值是否接近 1，且叉乘积的模是否接近 0，来判断该点是否为血管中的点。实验结果表明，对肝脏血管的分割，该算法能够快速有效地分割出更多更精细的血管。八元数这一高维的数学工具，在计算过程中综合考虑多个特性，与少量特性进行处理的结果相比较，有着明显的优势，相对于传统的血管分割算法，提高了血管分割的精度。

八元数；Cauchy积分公式；血管分割；三维重建

0 引言

医学图像的三维重建是医学图像可视化工作的核心。而针对二维医学图像的目标分割是三维重建的重要前提。如何使得分割目标更精细、更准确，取决于对分割方法、数学工具的选择[1-5],现阶段的分割方法主要采用区域生长[6]、边缘提取[7-8]、神经网络[9-11]、模糊连接[12-14]、微分算子[15]、活动轮廓[16-17]分水岭[18-19]等方法。

区域生长基本方法是以一组种子点开始，将与种子点性质相似的相邻像素附加到生长区域的每个种子上。传统的区域生长算法[20-25]一般只考虑种子点本身的灰度信息。计算时，将相似度大于设定阈值的像素计入到种子点所在的区域，最终形成一个或多个相似像素组成的连通区域。但在CT等造影图像中，常存在一定量的噪声，采用此方法会将因噪声而断裂的血管作为非相似像素处理，导致分割出的血管不够精细、多样；另外，生长的过程本身也没有考虑到血管的结构及走向，因此存在一定的弊端。而将八元数或clifford 代数等高维数学与区域生长的思想结合起来能克服上述缺点，并能分割出更细小的、不连续的血管。Cauchy 积分公式是复分析、四元数、八元数分析中的重要公式。其几何意义是：在光滑区域中封闭光滑形状内的任意一点可以用其边界上的点表示。因为人的血管具有光滑的特性，基于此，可以根据血管走向构造合适的封闭形状，并用封闭区域边界上点的灰度值平均来表示种子点，提高了算法的抗噪性。

八元数 Cauchy 积分公式是八元数解析函数理论的基石，在八元数分析中有着非常重要的作用，其几何意义是在光滑区域中，封闭光滑形状内的任意点可以用其边界上的点表示。均值定理是 Cauchy 积分公式的推论，复变函数中的均值定理介绍如下：若函数f(z)在复平面上某个区域是解析的，那么，该函数在区域内任意一点的取值等于函数在以该点为中心的圆周上取值的平均。其几何意义是光滑区域中，单位球中心的取值可以用球面上的数值的平均表示。

刘伟[26]首次提出将八元数 Cauchy 用于多分量图像边缘检测中。构造八元数 Cauchy 滤波器，即高维数的 Laplase 滤波器，并将其用于基于 RGB 联合 HSI 空间的彩色图像中，获得了较好的效果；武伟[27]将八元数Cauchy 积分公式用于 CT 序列图像提取肝脏，其算法相对于邻接区域生长算法等传统算法能够更好地保持肝脏边缘信息，分割出的无关区域也较少。考虑到人体血管具有光滑特性，血管走向也有一定规律可循，因此，本文将八元数 Cauchy积分公式用于肝脏血管的分割中。现有的血管分割方法，对血管的分割精度尚有不足，不能很好地满足临床的需求。

1 八元数Cauchy积分的血管分割算法

针对三维血管分割的特点及八元数 Cauchy 积分公式在三维图像处理中应用的优势，数据模型建立时考虑了如下因素：(1)三维空间内，血管走向大多倾向于垂直方向，血管垂直走势同时存在一定倾斜性；(2)利用像素点周边数据点的特征来代替中间数据点的像素值，避免了图像数据中奇异点的影响，同时提高了算法的抗噪能力；(3)没有与其他算法结合，而是直接利用数学性质来进行分割。这样算法不会受到引入算法的限制。算法流程图如图1。

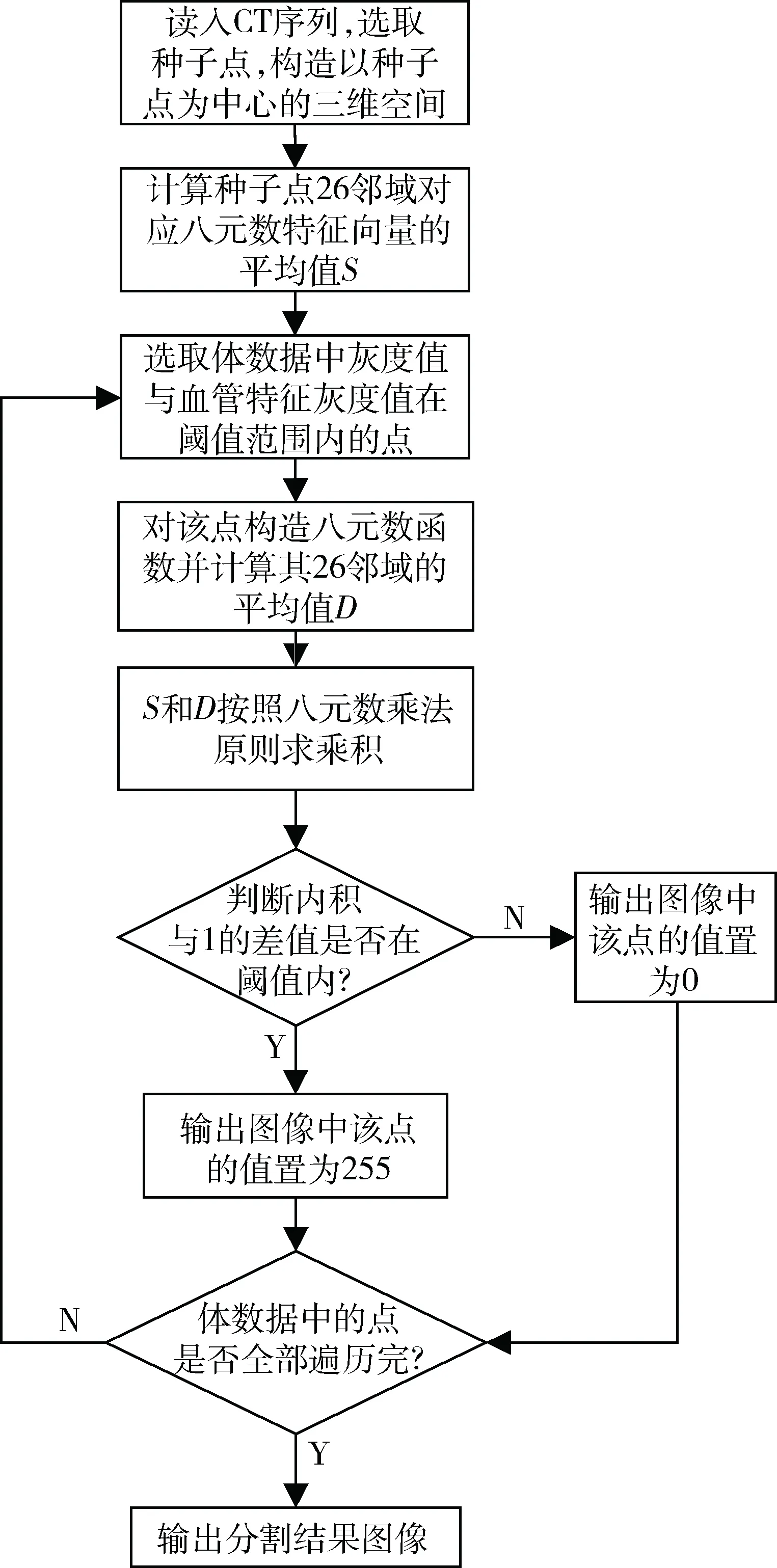
图1 算法流程图

1.1八元数的Cauchy积分公式

八元数O是由J.I.Graves和Cayley于1844～1845年发现的，是一种非交换、非结合的八维代数[28]。八元数的 Cauchy 积分公式是八元数分析的重要结论，均值定理是 Cauchy 积分公式的重要推论。八元数解析函数、Cauchy 积分公式及其均值定理的内容如下：

定义[28]：设f(x)∈C∞(Ω,O)，如果

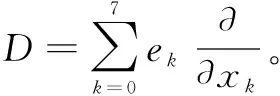
定理1[29](柯西型积分公式)：设Ω是R8中的连通开集，M是Ω内八维紧致定向C∞流型，M及其边界均含于Ω中。令

若f(x)在Ω内是左O-解析，即Df=0，则：

其中ω8是R8中的单位球面的面积。

定理2[28](八元数的均值定理)：设Ω是R8中的连通开集，Br(z0)是以z0为中心、半径为r的球，Br(z0)⊂Ω，如果Df=0，则

八元数 Cauchy 积分公式是八元数解析函数理论的基石，在八元数分析中有着非常重要的作用。均值定理是 Cauchy 积分公式的推论，其几何意义是光滑区域中，单位球中心的取值可以用球面上的数值的平均表示。考虑到人体血管具有光滑特性，血管走向也有一定规律可循，因此，本文将八元数 Cauchy用于肝脏血管的分割中。

1.2基于八元数Cauchy积分公式的血管分割算法

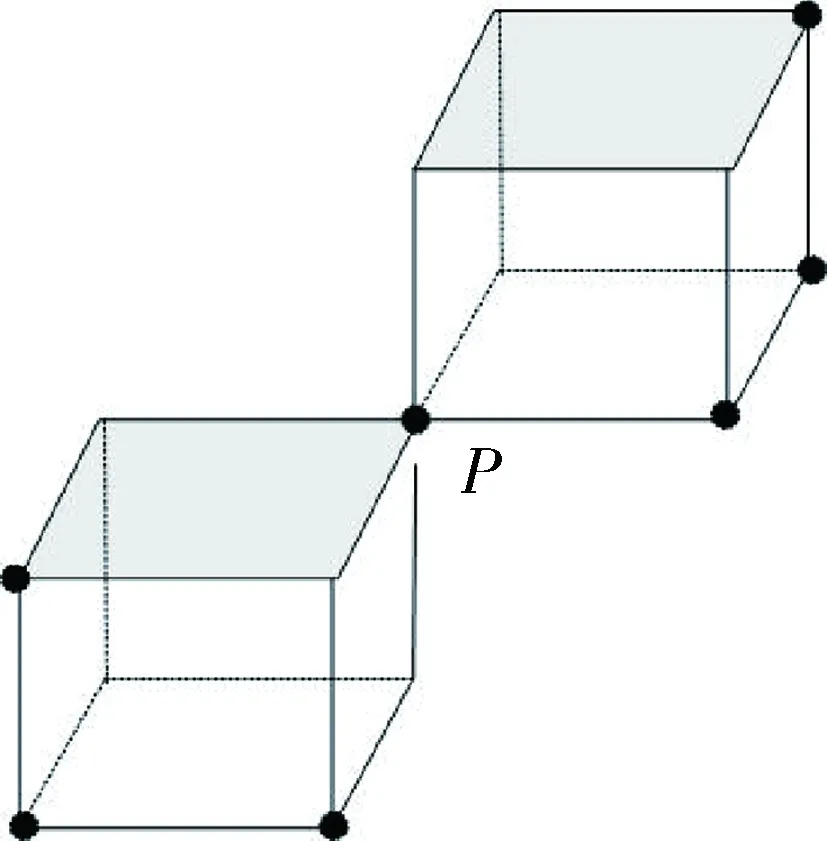
图2 六维向量示意图

算法使用医学图像处理工具 VTK、ITK 在系统内构成三维体数据。在体数据中，定义图像所在的平面为横纵轴平面(X-Y平面)，序列方向为竖轴(Z轴)，每个像素点都有唯一的坐标值。手动选择血管点像素，考虑到血管斜方向较多的走向规律性，选择了如图2所示的六维方向上的邻域像素代表当前数据特征点，从而构成一个纯八元函数。对于其他的数据，按照同样的数据表征结构来定义对应的纯八元函数。

具体过程为：

首先需要对CT序列图像建立八元数的模型。设当前点的坐标值为(x,y,z)，其像素值用f(x,y,z)表示。构造的纯八元数Oseed 如下所示：

Oseed=f(x,y,z-1)e1+f(x,y,z+1)e2+f(x-1,y,z)e3+f(x+1,y,z)e4+f(x,y-1,z)e5+f(x,y+1,z)e6

对其进行单位化得到种子点的特征向量O如下，用f1,f2,…,f6表示Oseed 的每一分量。

一般认为血管区域是平滑的，八元数的 Cauchy 积分定理成立。那么血管局部同质区域中，某一点的数值应等于以该点为中心的区域边界上取值的平均。使用如图3的封闭区域为研究对象，使用该区域边缘的 26 邻域的平均代表当前点的特征，使用该特征进行血管区域的提取。

图3 26邻域示意图

选择血管中的一点作为种子点，使用种子点的 26 邻域上的八元数的平均作为种子点的特征向量，遍历图像数据，用种子点的特征向量与每一点的特征向量做内积，通过判断内积值是否接近 1，来判断该点是否为血管中的点。

由于需要遍历所有体素点，并且对三维体数据的每一个体素点都构造一个八元函数，并计算其 26 邻域的平均值，因此，计算量很大，为减小数据量，本文只选择体数据中灰度值与血管特征点灰度值相差在一定范围内的数据点参与计算。血管特征向量与数据点对应的特征向量做内积。利用八元函数乘法性质对特征点八元函数与数据点八元函数的乘积来区别像素点，得到的内积值越接近 1，且叉积的模越接近 0，则说明数据点越有可能是血管点。设定精确的限定值，在精确度允许的范围内的点为血管点，将判定为血管点的值及其坐标位置对应输出。所有血管点输出完成，即为分割的最终结果。具体算法流程如下：

(1)输入腹部的 CT 序列图像。对图像进行预处理，利用反分割系统将骨骼去除。

(2)在血管区域选择种子点，种子点的特征向量使用其26邻域构成八元数向量。

(3)遍历图像中的数据，选择在灰度值阈值范围内的像素，计算每个像素的特征向量，并与种子点的特征向量作内积。判断内积与 1 的差值是否在给定的阈值范围内。

(4)如果是，则输出图像中该点的值置为 255，否则置为 0。输出图像即为分割出的血管。

2 实验结果与分析

本章的实验在 WIN7 系统上进行，CPU 2.4 GHz×2，内存大小为4 GB。使用ITK+VS2010b 编码。实验数据为S70肝脏血管系统造影CT图像(图像大小为512×512×320)，选取的阈值为0.05。

考虑到提取血管精细程度，没有对图像做滤波去噪等预处理，只是调整图像窗宽窗位充分显示血管结构，使图像在0～255像素灰度空间得到较好的显示，手动选择肝脏血管点参与算法计算。本章算法选取位置(136,247,162)处的血管点六维邻域构建血管点八元函数。

另外，三维分割算法生成三维的分割结果，在观察实验结果时，可以通过以下两种方式来直接观察。

(1)通过三维体数据中特定的切片图像查看；

(2)将分割后的切片数据序列进行三维重建后显示实验结果。

对于S70,取第109张CT切片，如图4所示。

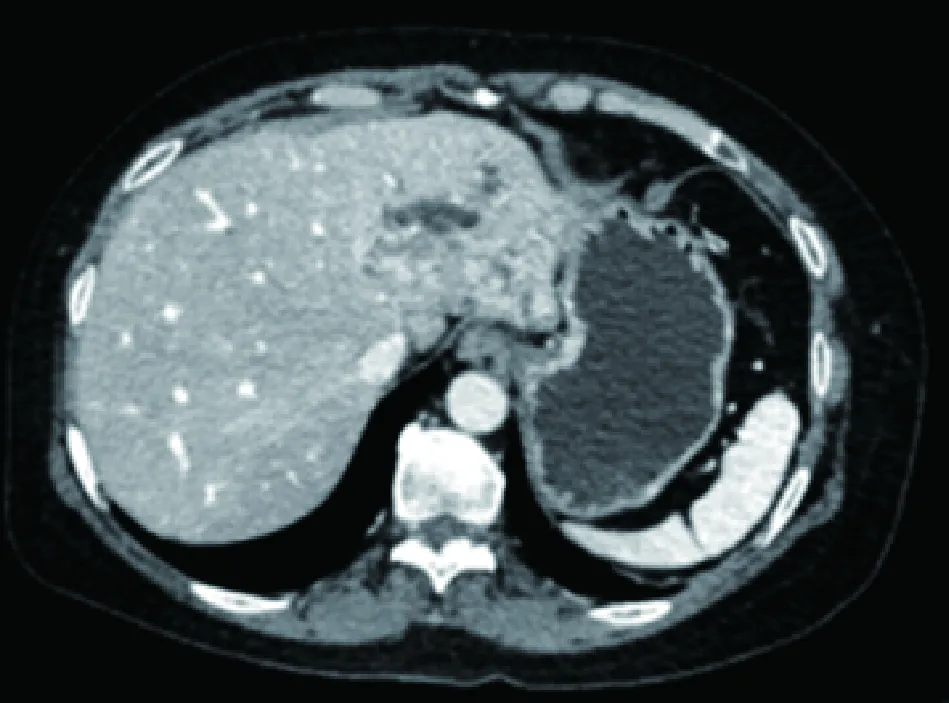
图4 S70第109张CT切片

分别使用本文算法与区域生长算法分割后，各个切片的结果如图5所示。

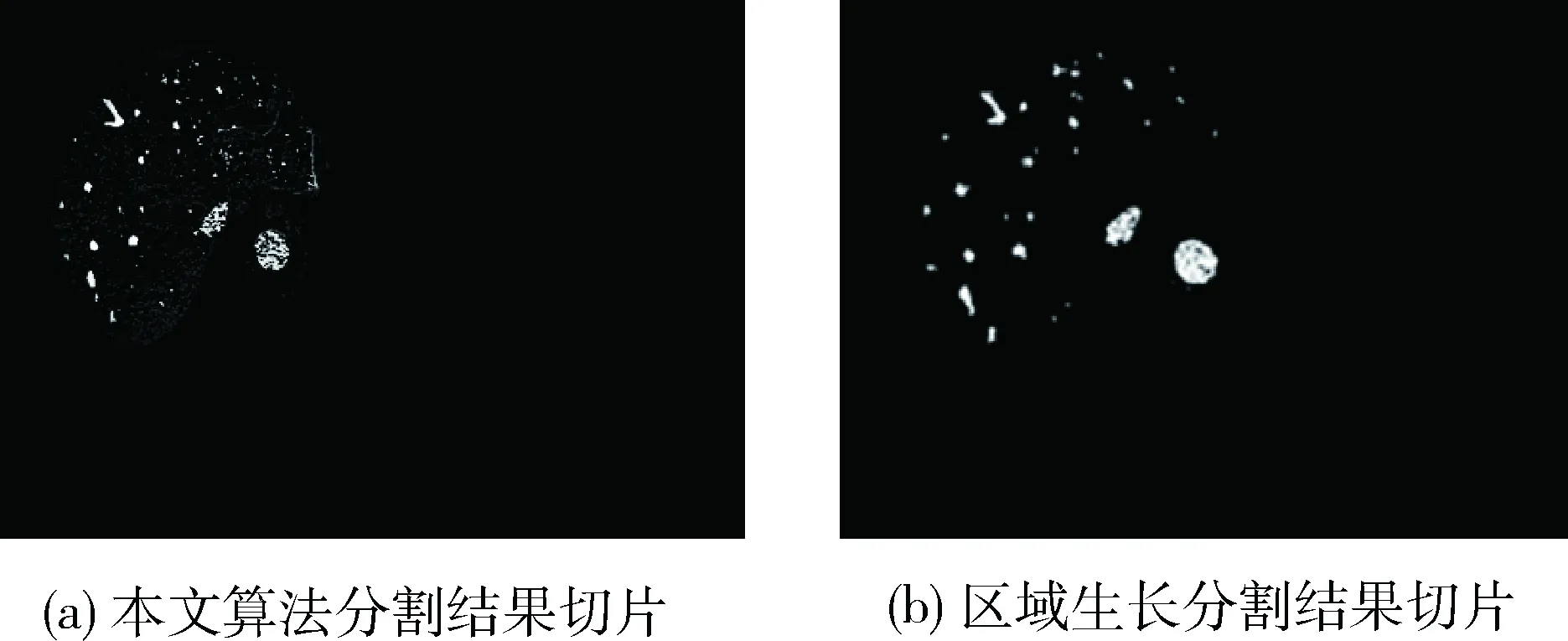
图5 S70二维切片的分割结果图

对两种不同算法的分割结果分别进行三维重建得到的血管模型如图6所示。

图6 三种算法对S70肝血管分割重建结果图

由于每一个像素点对应的八元函数都需要用封闭区域的边缘点像素对应的八元函数的平均来代替，并迭代地进行内积运算，耗时较多。但从实验结果可以看出：使用八元数Cauchy 积分公式这一高维的数学工具，与传统的区域生长算法相比较，提高了三维重建的精度，对于图像缺失断裂或噪声污染具有很好的适用性。此方法能分割出更精细的血管，对临床诊断和手术具有重要意义。

3 结论

医学图像分割是医学图像处理中的关键步骤，也是诸多学者研究的热点和难点。本文在此基础上继续挖掘、利用高维代数上的分析理论用于高维图像的处理当中并做血管的精细化分割。人的血管具有光滑的特性，基于此，本文将八元数 Cauchy 积分定理应用于血管的分割中。在计算过程中综合考虑血管走向、邻接多个像素点等，与仅考虑像素本身的方法相比较，在抗噪性、分割的精细度方面有明显的提高。

[1] 罗希平，田捷,诸葛婴，等. 图像分割方法综述[J]. 模式识别与人工智能，1999，12(3)：300-312.

[2] 宋余庆，谢丛华. 数字医学图像 [M]. 北京：清华大学出版社, 2008.

[3] 于志强.医学图像分割与虚拟手术几个关键问题的研究[D].上海:上海交通大学,2007.

[4] 潘家辉, 鲍苏苏, 朱志有, 等. 支持力反馈的肝脏外科虚拟手术仿真系统 [J].计算机工程, 2008, 34 (21): 262-264.

[5] 翟伟明. 影像引导下计算机辅助介入手术导航关键技术的研究 [D]. 北京: 清华大学, 2010.

[6] 彭丰平, 鲍苏苏, 曾碧卿. 基于自适应区域生长算法的肝脏分割[J]. 计算机工程与应用, 2010, 46(33):198-200.

[7] LI M J, DONG Y B, WANG X L. Medical image edge detection analysis method based on fractional differential[J]. Advanced Materials Research, 2013, 860-863:2859-2863.

[8] 李波, 梁攀, 关沫. 一种基于边缘提取的交互式图像分割算法[J]. 微型机与应用, 2013, 32(10):41-44.

[9] Lü Chaohui, Chen Xiaoguang, Wu Wenfu, et al. Segmentation of the seedling image by BP neural network[J]. Transactions of the Chinese Society of Agricultural Engineering, 2001, 39(4): 337-348.

[10] Ma Y.The application of octonion and BP neural network in liver vessel segmentation[D].Guangzhou:South China Normal University, 2014.

[11] 王锦程, 郁芸, 杨坤,等. 基于B P神经网络的脑肿瘤MRI图像分割[J]. 生物医学工程研究, 2016, 35(4):290-293.

[12] ROSENFELD A. On connectivity properties of grayscale pictures [J]. Pattern Recognition, 1983, 16(1): 47-50.

[13] ROSENFELD A. Fuzzy digital topology[J]. Information and Control, 1979, 40(1):76-87.

[14] 张玲. 基于模糊理论及其扩展的图像分割研究及应用[D]. 济南: 山东大学,2012.

[15] 李军成. 图像边缘检测的分数阶微分算子研究[J]. 计算机应用与软件, 2015, 32(12):206-209.

[16] KASSM, W ITKN A, TERZOPOULOSD. Snake: Active contourmodels[J]. International Journal of Computer Vision, 1987, 1(4): 321-331.

[17] 段丁娜, 张欢, 邱陈辉,等. 基于活动轮廓模型的图像分割算法综述[J]. 中国生物医学工程学报, 2015, 34(4):445-454.

[18] 王改云, 杨小娟. 融合分水岭和区域生长的图像分割算法研究[J]. 微型机与应用, 2014,33(10): 30-32.

[19] 何鹏, 王成琳, 王福刚. 基于改进分水岭算法的熏烤肉图像分割[J]. 电子技术应用, 2012, 38(10): 126-128.

[20] ADAMS R, BISCHOF L. Seeded region growing [J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 1994, 16 (6): 641-647.

[21] 程明,黄晓阳,黄绍辉,等.定向区域生长算法及其在血管分割中的应用[J].中国图象图形学报,2011,16(1):44-49.

[22] 刘鑫, 陈永健, 万洪林,等. 基于两阶段区域生长的肝内血管分割算法[J]. 计算机工程与应用, 2015, 51(12):194-197.

[23] DEL FRESNO M, VÉNERE M, CLAUSSE A. A combined region growing and deformable model method for extraction of closed surfaces in 3D CT and MRI scans[J]. Computerized Medical Imaging and Graphics, 2009, 33(5): 369-376.

[24] PALOMERA-PÉREZ M A, MARTINEZ-PEREZ M E, BENTEZ-PÉREZ H, et al. Parallel multi-scale feature extraction and region growing: application in retinal blood vessel detection[J]. Information Technology in Biomedicine, IEEE Transactions on, 2010, 14(2): 500-506.

[25] ZANATY E, ASAAD A. Probabilistic region growing method for improving magnetic resonance image segmentation[J]. Connection Science, 2013, 25(4): 179-196.

[26] 刘伟. 八元数及 Clifford 代数在数字图像处理中的应用[D]. 广州：华南师范大学, 2010.

[27] 武伟. 八元数分析系和钱方法在数字图像处理中的应用研究[D].广州：华南师范大学, 2014.

[28] 李兴民.八元数分析[D]. 北京: 北京大学, 1998.

[29] LI X,PENG L.The Cauchy integral formulas on the octonions[J]. Bulletin of the Belgian Mathematical Society-Simon Stevin, 2002, 9(1): 47-64.

Vessel segmentation algorithm based on octionion Cauchy integral formula

Wang Xiaochan1, Wu Mingzhu2, Li Xingmin3

(1. Library, Southern Medical University, Guangzhou 510515, China;2. Computer Department, Guangzhou College of Commerce, Guangzhou 511363, China;3. School of Computer, South China Normal University, Guangzhou 510631, China)

Because of the influence of the noise in the image, the cracked blood vessel can not be separated, which leads to the problem that the segmentation precision is not high enough. This paper proposes a new three-dimensional region growing algorithm based on high dimensional mathematical tools：octonion vector product. The proposed method first uses traditional region growing algorithm to segment continuous blood vessels. The edges of the vessel are found by gradient calculation and they are used to be initial seeds in the octonion growing regions. Then the six neighborhood of seeds’ gray are used to construct octionions which represent the characteristics of seeds. The octonion vector product operation is used to connect the rupture vasculars which are under the influence of noise. Experimental results of the liver vessel segmentation show that the algorithm can quickly and efficiently segment more vessels. This octonion mathematical tools of high dimensions, which can consider multiple characteristics in the process of calculation, and this method has obvious advantages compared with the traditional vascular segmentation algorithm, and improved the accuracy of blood vessel segmentation.

octonion; Cauchay integral formula; vessel extraction; 3D reconstruction

国家高技术研究发展计划(863计划)(2012AA021105)

TP391

：A

10.19358/j.issn.1674- 7720.2017.17.013

王晓婵，吴明珠，李兴民.基于八元数Cauchy积分公式的血管分割算法[J].微型机与应用，2017,36(17)：45-48,55.

2017-03-03)

王晓婵(1988-)，女，硕士，助理馆员，主要研究方向：数字图像处理。吴明珠(1982-)，女，硕士，讲师，主要研究方向：数字图像处理，计算机仿真。李兴民(1957-),男，博士，教授，主要研究方向：小波分析、八元数分析、数字图。