基于梯形波磁化电流的便携式磁粉机能耗优化方案

麦志恒，王 杰，费跃农

(深圳大学 机电与控制工程学院，深圳 518060)

基于梯形波磁化电流的便携式磁粉机能耗优化方案

麦志恒，王 杰，费跃农

(深圳大学 机电与控制工程学院，深圳 518060)

通过对便携式磁粉机磁化电流的研究，发现在方波磁化电流模型下，磁轭线圈容易在电流换向时出现尖峰电流。提出了一种基于梯形波的优化磁化电流模型，使磁轭线圈电流平缓换向，解决了尖峰电流带来的高能耗和潜在的对电路损害的问题。试验结果表明，优化的磁化电流模型能减少电池输出电流的31.96%，使磁粉机的续航时间提升46.98%，具有一定的参考价值。

梯形波；便携式磁粉机；能耗优化；磁化电流

便携式磁粉机的结构简单、重量轻，适用于磁粉检测的多种工作环境，在无损检测中得到广泛应用。

文中讨论的便携式磁粉机为交叉磁轭式，并由两路不同相位的高压直流方波信号进行磁化。其中，高压直流信号由12 V锂电池逆变而成。此交叉磁轭形成的磁场，同时具备交流磁化和直流磁化的优点，工件表面缺陷检测灵敏度高，缺陷检测深度大。

但在试验过程中，发现磁轭线圈的电流换向时容易产生尖峰电流[1]。这不仅导致磁粉机耗能过高，降低了电池续航时间，而且容易损坏晶体管及驱动电路。

笔者提出了一种基于梯形波的磁化电流模型，在保证提升力和检测灵敏度的前提下，解决了尖峰电流问题，提升了电池的续航能力。

1 便携式磁粉机检测原理

1.1便携式磁粉机工作过程

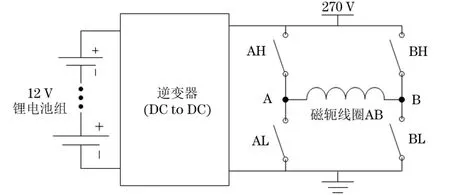
图1 便携式磁粉机主电路示意

笔者介绍的便携式磁粉机主要包括便携电源和交叉磁轭两部分[2]，其中，便携电源由12 V锂电池和主电路组成，便携式磁粉机主电路如图1所示；磁轭工作过程如图2所示，交叉磁轭由两个夹角为90°的磁轭AB、CD组成，如图3所示。通过逆变器产生270 V高压直流电源，4个N沟道MOS管组成单个磁轭的H桥驱动电路。

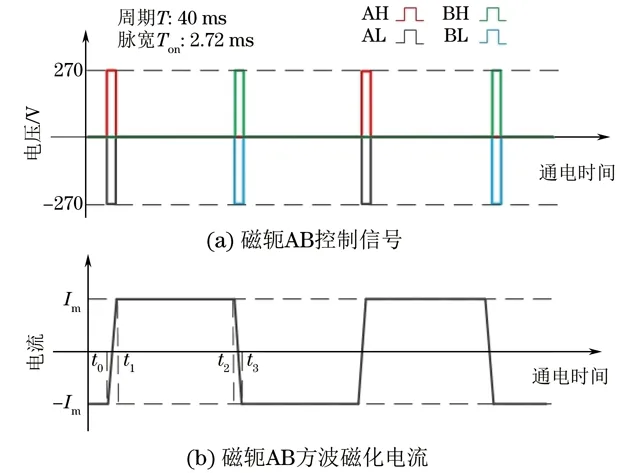
图2 磁轭工作过程示意

图3 交叉磁轭示意

以磁轭线圈AB为例，通过控制桥臂AH、BH、AL、BL的“闭合”或“断开”状态产生高压方波，从而控制磁轭线圈的磁化电流。

磁轭工作过程可分为4个阶段：

(1)t0t1阶段，AH、BL闭合，BH、AL断开，高压信号通过线圈A到B产生正向磁化电流，并在t1时刻到达峰值电流Im。

(2)t1t2阶段，AL、BL闭合，AH、BH断开，此时磁轭线圈等效于RL零输入模型，其电流响应曲线近似图2中t1t2段。

(3)t2t3阶段，BH、AL闭合，AH、BL断开，高压信号通过线圈B到A产生反向磁化电流，故IAB先减少为0，再反向增大到-Im。

(4) 不断循环(1)(3)通电过程。由于电流上升/下降时间极短，所以磁化电流近似于方波。

同样，磁轭CD中通有相同幅值和脉宽的方波磁化电流，并与磁轭AB有90°相位差。

1.2交叉磁轭形成的旋转磁场

由便携式磁粉机工作过程可知，两磁轭在直流稳态情况下产生的直流磁场符合矢量叠加原则；同时方波磁化电流还可分解成各阶奇次正弦谐波，又由于两磁轭磁化电流存在相位差，所以能够产生类似交流电磁轭所形成的旋转磁场。

该旋转磁场数学模型[3]可表示为

式中：Hx为磁场强度在x轴方向的分量；Hy为磁场强度在y轴方向的分量；N为线圈匝数；K为比例常数；θ为两线圈夹角；φ为磁化电流的相位差。

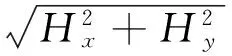
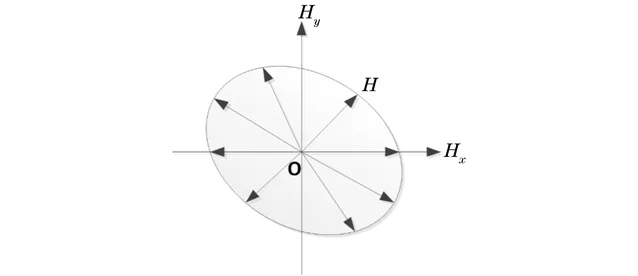
图4 旋转磁场分布示意

1.3磁粉的受力运动在湿法磁粉检测中，磁粉受到工件缺陷处变化的漏磁场磁力、重力、浮力和摩擦力的作用，而磁粉运动距离ΔS取决于所受到的合力及磁化时间Δt。当ΔS>S0(S0为磁粉移动的距离)时，磁粉能被吸引到缺陷处，产生明显磁痕；反之，则不能形成明显磁痕[4]。因此，保证磁粉所受到的合力能使其在磁化时间Δt内能运动到磁痕处，是磁粉检测的基本要求。

2 方波磁化电流模型

2.1方波磁化电流模型傅里叶级数展开

任何周期函数f(t)都可以用正弦函数构成的无穷级数来表示，在验证性试验中，交叉磁轭线圈的磁化电流近似为周期和幅值固定，且有90°相位差的方波电流，方波磁化电流模型如图5所示。

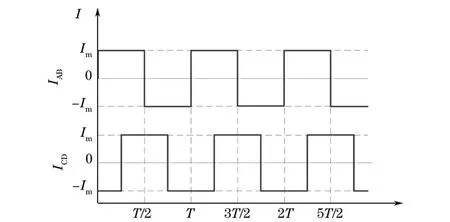
图5 方波磁化电流模型

将方波电流IAB展开为傅里叶级数：

由式(2)可知，方波电流IAB和ICD中包含了各频率的奇次正弦谐波。根据1.2节描述的旋转磁场产生原理，该方波电流符合形成旋转磁场的条件。

2.2方波磁化电流模型试验

为了验证方波磁化电流在实际应用中的可行性，笔者进行了试验，试验条件如下所述。

(1) 磁轭提升力不小于118 N，即能平稳提起质量为12 kg的铁块。

(2) 灵敏度：使用A1-15/50试片，人工缺陷能清晰显示。

(3) 使用12 V、8 A的锂电池进行测试。

(4) 交叉磁轭的间距为80 mm，磁轭截面为20 mm×20 mm。

(5) 磁轭线圈匝数保持不变。

经过反复试验，确定该磁轭的最佳工作频率为25 Hz。在该频率下能够平衡检测灵敏度和整机能耗到最优，因此选取25 Hz控制信号进行试验具有代表性。方波电流模型试验结果如表1所示。

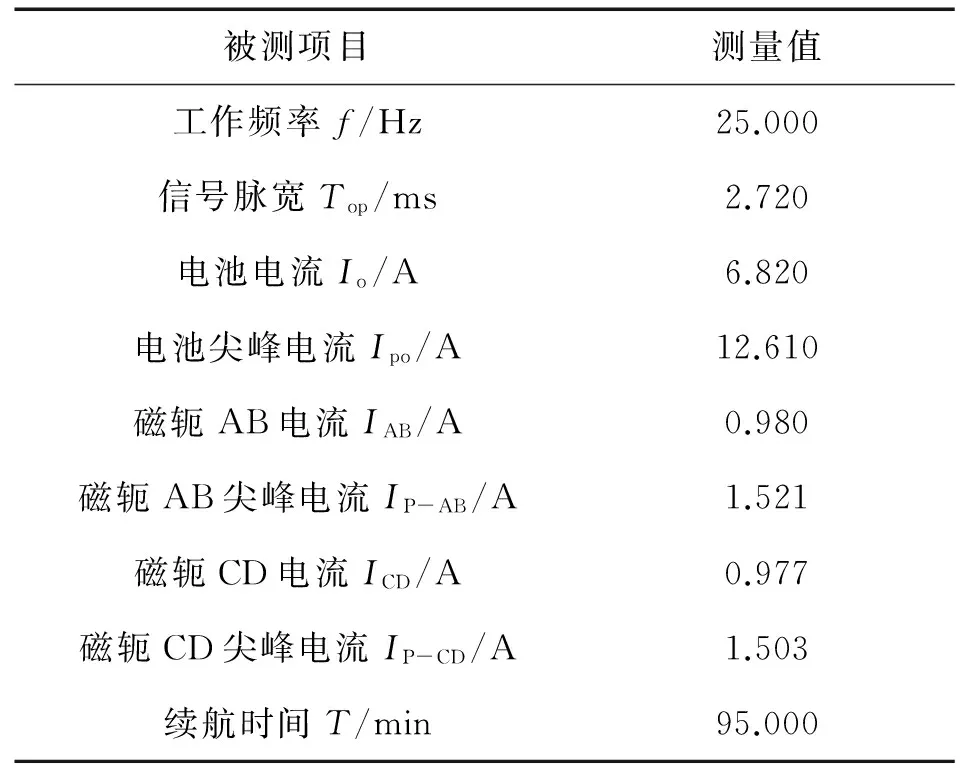
表1 方波电流模型试验结果

方波磁化电流如图6所示，由表1和图6可见，在方波磁化电流模型试验中，磁轭AB或CD在每次电流换向时出现尖峰电流IP-AB和IP-CD，该电流为磁轭线圈有效电流值的1.55倍。当负载端(线圈电流)急速上升并出现尖峰电流时，瞬时功率P增大，负载端需要从逆变器获取更多的能量，使逆变器的导通时间也增加，从而引起电池电流也出现瞬时尖峰电流，根据表1可知，电池尖峰电流达到了12.6 A。由于电池容量的限制，过大的电流输出会严重损害锂电池，不利于长期使用，同时瞬时电流过大也有烧坏保险丝、击穿电路等危害。

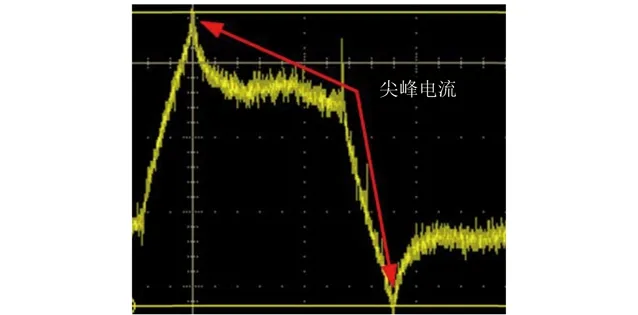
图6 方波磁化电流

为了消除线圈尖峰电流，减小电池电流输出，最大程度提高便携式磁粉机续航时间，并保护驱动电路，考虑采用一种分段控制信号的策略来抑制尖峰电流的出现，达到优化磁化电流的效果。

3 梯形波磁化电流模型

3.1梯形波磁化电流模型构建

将单个方波脉冲信号分为15段短脉冲，总脉宽为10 ms，周期依旧为40 ms。根据线圈电流反馈，将15段脉冲信号设置为不同脉宽。前几个脉宽较大，使线圈电流快速换向；后几个脉宽小，使线圈电流平缓上升到最大值Im。这样既抑制住了尖峰电流，也保证了线圈电流的有效值，从而保证了磁轭检测的提升力。在这种分段控制策略下，电流换向时间延长，上升变平缓，可等效为梯形波磁化电流。梯形波磁化电流如图7所示。

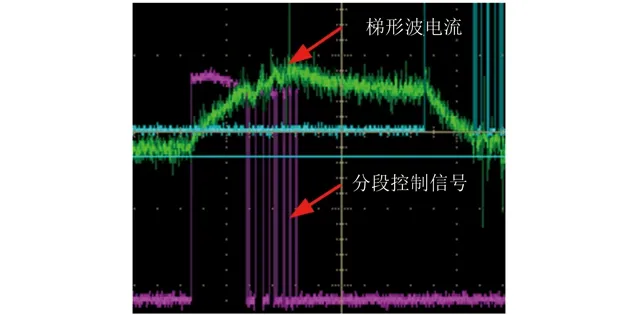
图7 梯形波磁化电流

3.2梯形波磁化电流模型傅里叶级数展开

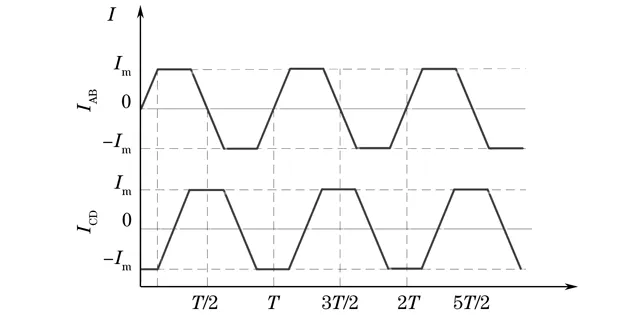
图8 梯形波函数模型

构建梯形波函数模型如图8所示。

将梯形波电流IAB按傅里叶级数展开：

由式(3)可知，梯形波电流IAB和ICD也可展开成含有奇次项的正弦谐波[5]。

3.3方波与梯形波的频谱对比

绘制方波和梯形波信号的频谱图，如图9所示。方波信号和梯形波信号的频谱幅值趋势大致相同，即都是随着频率的增大，奇次谐波衰减得更快。在磁粉检测中，低频主要表现在穿透力上，高频主要表现为趋肤效应，但就整体频率分布而言，梯形波与方波信号的磁粉检测能力相当。只是在低频阶段，方波具有更好的穿透力。

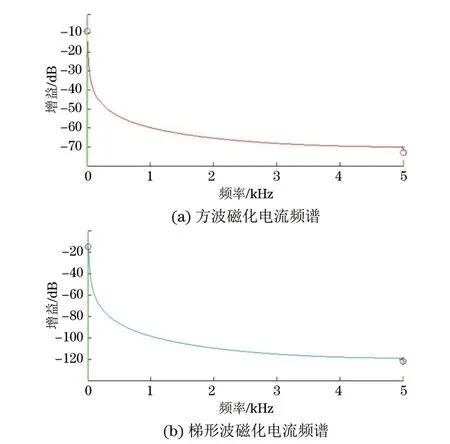
图9 方波和梯形波磁化电流频谱

在高频段，为了说明电流密度在导体内的衰减程度，引入穿透深度δ，其定义是电流密度衰减到导体表面处的1/e时透入导体内的距离，可以证明δ为

式中：f为交流电频率，Hz；u为导体的相对磁导率；∂为导体的电导率，S·m-1。

在检测的过程中，导体的相对磁导率和导体的电导率是固定不变的，所以当频率增大时，检测的穿透深度也会越来越集中在近表面。现假设一磁性钢棒，半径为2 cm，相对磁导率u为500，电导率∂为1.27×106S·m-1。当f为100 Hz时，则由式(4)可得，穿透深度为1.99 mm；f为1 000 Hz时，穿透深度为0.63 mm，f为1 MHz时，穿透深度为0.02 mm。可见，随着频率的升高，电流密度也会集中在导体的极薄处，这种现象称为趋肤效应[6]。

由此可知，梯形波和方波磁化电流模型一样含有低频和高频的奇次谐波，可以用于磁粉检测中。

3.4梯形波磁化电流试验

对梯形波磁化电流进行试验，在与方波磁化电流试验条件一致的情况下，试验结果如表2所示。

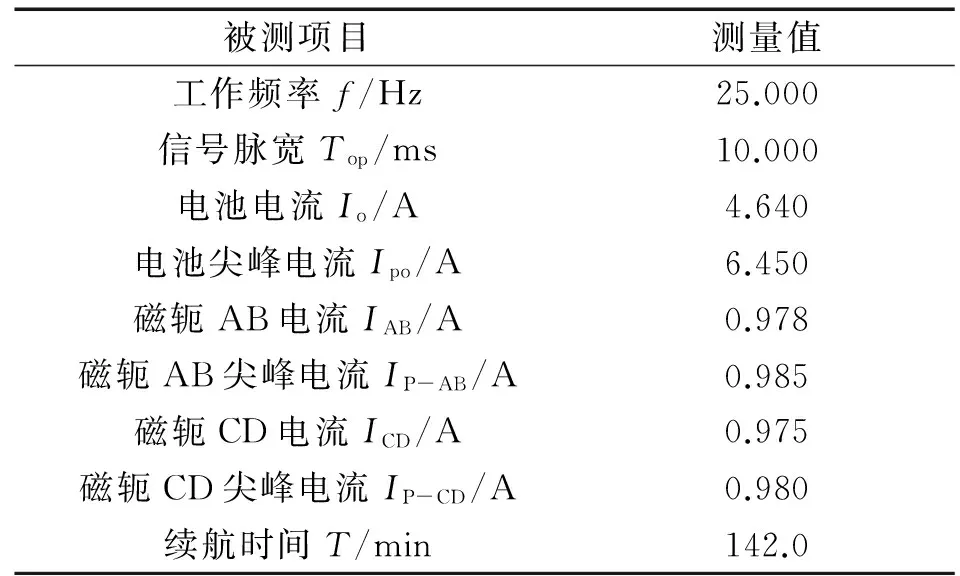
表2 梯形波磁化电流模型试验结果

由表2和图7可知，梯形波磁化电流模型中，磁轭原先出现尖峰电流的部分被缓慢增长的电流曲线代替了，尖峰电流被完全消除。而磁轭的有效电流与方波模型相当，保证了提升力和灵敏度的需求。同时可见整机电流显著减小了31.96%。电池续航时间提升到46.98%，使得便携式磁粉机的续航能力得到极大的提升。

4 结论

便携式磁粉机在实际使用过程中，除了保证提升力、灵敏度基本参数外，最重要的是提升装置的续航能力，从而提高检测人员的现场作业效率。在保证便携电源设备不变的情况下，所提出的梯形波电流模型在原有方波电流模型的基础上续航时间增加了46.98%，大大地提高了装置的使用效率。同时，通过分段控制信号很好地抑制了尖峰电流，在减少耗能的同时，保护了电路设备，尤其是避免了电池的过高输出。所以该方案在便携式磁粉机的实际设计中具有很好的参考价值。

[1] 李本事, 华娜, 赵希龙.电流波形和试块对三相全波整流电磁粉检测系统性能测试的影响[J]. 无损检测, 2016, 38(5): 34-37.

[2] 朱万钦, 张彦奎, 王恒迪,等. 多功能便携式磁粉探伤仪的研制[J].无损探伤,2015,39(4):29-31.

[3] 杨文峰, 陈君平, 伊建锋, 等. 磁粉检测中交叉磁轭的灵敏度探讨[J]. 无损检测, 2010, 32(11): 868-876.

[4] 郑国恒, 张柯, 周瑶,等. 便携式磁粉探伤机设计的关键技术[J]. 无损检测, 2010, 32(4): 267-270.

[5] 张其善, 王钢, 韦玉川. 基于梯形波分析信号的一种新方法[J]. 电子学报, 2001(4): 560-562.

[6] 陶旺斌. 论磁化电流[J]. 无损检测, 1995,17(3): 81-85.

EnergyConsumptionOptimizationSchemeofPortableMagneticPowderMachineBasedonTrapezoidalWaveMagnetizingCurrent

MAI Zhiheng, WANG Jie, FEI Yuenong

(College of Mechatronics and Control Engineering, Shenzhen University, Shenzhen 518060, China)

By the research of square wave magnetizing current model of portable magnetic powder machine, it is found that the yoke coil will cause the peak current when the current of coil is reversing. In this paper, a magnetization current model based on trapezoidal wave is proposed. It makes the coil current of the magnetic yoke reverse smoothly and reduces the peak current to avoid the peak current damage to the drive circuit. The experimental results show that the optimization model can reduce the average current of the battery by 31.96% and improve the life time of the magnetic powder machine by 46.98%. It has certain reference significance.

trapezoidal wave; portable magnetic powder machine; energy optimal; magnetization current

TG115.28

： A

：1000-6656(2017)09-0015-04

2016-12-18

麦志恒(1993—)，男，硕士研究生,主要从事嵌入式无损检测设备研究工作

费跃农，feiyn@szu.edu.cn

10.11973/wsjc201709004