基于CEEMD能量熵与SVM的低速轴承故障声发射诊断

杨 杰，张鹏林，刘志涛，常 海

(兰州理工大学 省部共建有色金属先进加工与再利用国家重点实验室, 兰州 730050)

基于CEEMD能量熵与SVM的低速轴承故障声发射诊断

杨 杰，张鹏林，刘志涛，常 海

(兰州理工大学 省部共建有色金属先进加工与再利用国家重点实验室, 兰州 730050)

针对低速轴承故障诊断难的问题，将互补总体平均经验模态分解(CEEMD)能量熵与支持向量机相结合对低速轴承故障进行了声发射诊断。采集不同缺陷状态的轴承声发射信号进行CEEMD分解，得到自适应的本征模态分量(IMF)；结合IMF分量的方差贡献率和互相关系数对虚假分量进行剔除，筛选出有效IMF分量。对提取的有效IMF分量计算能量熵，作为不同故障轴承的特征向量。将该特征向量输入到支持向量机(SVM)，对不同故障的低速轴承进行分类识别。试验结果表明，通过方差贡献率和互相关系数能够筛选出含主要故障信息的IMF分量，同时验证了SVM相比BP神经网络对低速轴承不同故障类型的识别效果更好。

声发射；低速轴承；互补总体平均经验模态分解；能量熵；支持向量机；故障诊断

低速轴承作为重型旋转设备的关键部件之一，且承受的载荷大、运行工况复杂，在运转时容易产生故障而造成停机事故。据统计，旋转机械设备30%的损坏都是由滚动轴承引起的[1]。低速轴承的健康状况往往关系到大型旋转设备能否安全稳定的运转。因而，对低速轴承的损伤状况进行检测具有极其重要的意义。传统的检测方法如振动法、油液法、冲击脉冲法(SPM)等，对低速轴承故障诊断都存在诸多局限性，检测效果不佳[2-4]。

声发射(Acoustic Emission，简称AE)是材料产生变形或断裂时，局域源快速释放能量而发出高频应力波的现象[5]。轴承低速运转时，表面裂纹、磨损、点蚀、润滑不良等都会形成声发射源[6-8]。对于低速故障轴承声发射信号，从中提取轴承故障特征是研究的难点，而自适应时频分析法是处理非平稳声发射信号的最佳工具[9]。当前常用的自适应时频分析方法之一是经验模态分解(EMD)，该算法将非平稳信号分解为一系列本征模态分量(IMF)，从IMF分量各频带能量的变化来监测轴承的损伤状态。但该算法存在模态混叠现象，使得从原信号分解出的IMF分量会失真[10]。在此基础上，WU等[11]借助高斯白噪声均匀分布的统计特性，提出了集合经验模态分解(EEMD)算法，在一定程度上降低了EMD分解的模态混叠。但由于该算法是通过提高添加白噪声的集合次数来消除重构信号残余噪声的，计算成本较高[12]，并且添加的白噪声不能完全中和，不具备完备性。为了解决这个问题，YEH等[13]在EEMD基础上提出了一种改进算法，即互补集合经验模态分解(CEEMD)，该算法通过对信号添加正负成对的随机高斯白噪声，很好地消除了重构信号中的残余辅助噪声。如果轴承低速运转时产生故障，在不同频带的声发射信号能量会发生改变，而经过CEEMD分解后的各IMF分量从高频到低频依次分布，从而可通过各IMF分量能量熵的变化来判断轴承是否存在故障。

基于以上研究现状，笔者应用声发射技术对低速轴承的不同损伤状态进行了监测，将不同故障轴承的AE信号进行CEEMD分解，结合IMF分量的方差贡献率和互相关系数对虚假分量进行剔除，筛选出有效分量，并计算出有效IMF分量的能量熵。最后将其作为特征向量输入到多分类支持向量机，从而验证上述方法对低速轴承故障特征提取的准确性和可行性。

1 CEEMD算法

CEEMD算法是在EEMD基础上向原信号加入一对幅值相同、符号相反的辅助白噪声，这样能够降低添加噪声次数，并且很好地消除重构信号中的残余辅助噪声，提高了运行效率。EEMD也是一种噪声辅助的信号分解方法，其通过将待分析信号添加同等幅值高斯白噪声，并进行多次EMD分解，最后把分解后的IMF进行总体平均计算，从而将添加的白噪声互相抵消。EEMD分解还克服了小波分析中小波基函数和阈值选择的不确定性。其可以将待分析信号x(t)自适应分解为n个本征模态fi(t)和一个残余量r(t)，即：

提取的IMF分量要满足以下两个条件：① 在整个序列中，极值点数和过零点数相等或最多相差1；② 在任意一点，待分析信号局部极值点构成的上下包络线均值为0。但是实际应用中由于EEMD分解添加白噪声的次数不能无穷大，因而添加的白噪声不能完全被中和。

而CEEMD通过添加一对正负幅值相同的随机高斯白噪声，再进行EMD分解，使其能够最大限度地中和添加的白噪声，并且极大地减小信号重构误差，提取的信号特征也更加真实。CEEMD具体步骤如下：

(1) 将待分析信号x(t)添加一对幅值相同、符号正负相反的随机高斯白噪声ni(t)，形成新的两个分解信号

式中：x1(t)，x-1(t)为加入随机高斯白噪声的新分解信号；ni(t)为添加的高斯白噪声，该值可随噪声强度进行调整，一般取原信号标准差的0.01～0.5倍。

(2) 应用EMD算法对x1(t)和x-1(t)进行分解，得到各自的IMF分量c1(t)和c-1(t)，以及残余量r1(t)=x1(t)-c1(t)和r-1(t)=x-1(t)-c-1(t)。

(3) 重复n次步骤1和2，并且每次加入随机正态分布白噪声序列；直到残余量不能再被分解为止。最后将分解得到的IMF分量求均值，把该均值作为IMF分量的结果，即：

2 CEEMD能量熵

当低速轴承产生故障时，会有突发型声发射信号产生，并且轴承出现不同故障时，采集的声发射信号频率分布会发生改变。同时，轴承产生故障过程中各频带的能量分布也会产生相应变化，基于此引入CEEMD能量熵的概念。

通过对不同损伤状态轴承的原始声发射信号x(t)进行CEEMD分解得到n个IMF分量和一个残余量，计算出n个IMF分量c1,c2,c3…,cn和一个残余量rn，相应地求出n个IMF分量的能量分别为E1,E2,…,En。此处假设忽略残余量，在CEEMD分解正交性前提下，将n个IMF分量能量相加应等于原始声发射信号的总能量。CEEMD分解是从高频到低频依次分布的，分解的IMF分量c1,c2,c3,…,cn包含不同的频率带，且具有不同的能量，从而E={E1,E2,…,En}形成了不同缺陷轴承声发射信号能量在频率域的分布。由此可将CEEMD能量熵定义为

式中：Pi=Ei/E，为第i个本IMF分量的能量占总能量的比值，E为信号的总能量。

按该方法分别计算无缺陷、滚动体2 mm和外圈2 mm线缺陷轴承声发射信号经CEEMD分解后的能量熵。无缺陷轴承声发射信号的能量熵为1.334 4，滚动体线缺陷轴承声发射信号的能量熵为1.264 4，外圈线缺陷轴承声发射信号的能量熵为0.817 8。

上述结果证实了无缺陷轴承的CEEMD能量熵要比有缺陷轴承的熵大，这是因为当轴承无缺陷运行时，声发射信号的能量均匀分布在整个频带；当轴承产生缺陷时，在相应的频带会有能量集中的现象，从而使得整个频带能量分布的不确定性减小，能量熵相应减小。由于外圈故障相对滚动体故障信号传播衰减小，因而采集的外圈故障声发射信号更加真实，从而使得外圈存在故障时轴承的CEEMD能量熵最小。

从以上分析可知，通过CEEMD能量熵能够判断低速轴承的损伤状态和故障类型。为了对不同故障类型轴承进行模式识别，试验引入支持向量机对轴承不同故障信号进行训练和测试。

3 支持向量机

支持向量机(SVM)是建立在统计学习VC维理论和结构风险最小化原理基础上的优秀模式识别方法，可以有效克服小样本、过拟合、非线性等问题[14]。其中，学习机器的VC维反映了分类函数的学习能力，其值越大，学习模型越复杂。因此，在满足分类精度的同时，需降低VC维。与人工神经网络相比，SVM更好的泛化能力使其广泛应用于机械故障诊断领域。SVM通过核函数将非线性样本数据映射到高维空间，使得在这个高维空间非线性数据样本变成线性可分，从而在高维空间中构造出最优分类超平面。试验基于开源程序LIBSVM和MATLAB平台，该程序包是由台湾学者林智仁开发设计的[15]。该工具箱对于多分类问题采用一对一算法，并通过网格法对参数进行寻优计算。结合试验中3种不同状态的轴承情况，需设计3个SVM，从而对低速轴承故障类型进行识别。

4 低速轴承故障诊断实例分析

在自行设计加工的低速回转试验台上进行试验，该试验台可以实现轴承超低速运转(转速范围为1～5 r/min)。试验轴承采用圆锥轴承30207，其外径为72 mm，内径为35 mm；滚动体个数为17；轴承接触角α=18.25°。通过线切割分别对轴承外圈和滚动体加工2 mm线缺陷。为了重点分析轴承故障声发射信号特征信息，此处将无缺陷轴承、滚动体2 mm线缺陷轴承、外圈2 mm线缺陷轴承进行对比分析，图1分别为这3种类型轴承声发射信号的原始波形。

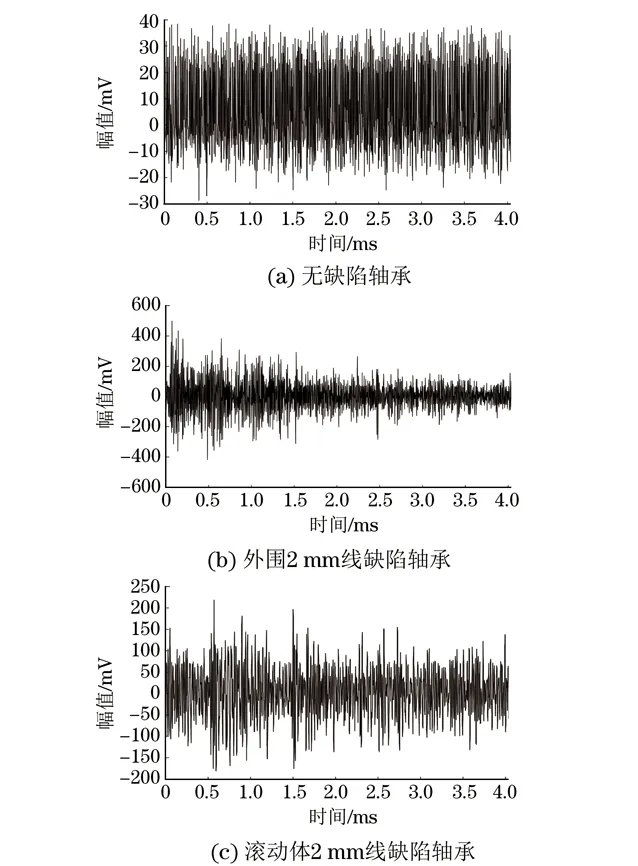
图1 圆锥轴承不同缺陷声发射信号原始波形

从图1中可以看出，当轴承无缺陷时，声发射信号比较平稳；当轴承存在缺陷时，在某一时刻会有突发型的AE信号产生。为了说明CEEMD算法的优势，首先对采集的所有损伤类型轴承的AE信号进行EEMD分解，得到10个IMF分量和一个残余量。通过文献查阅和多次验证，试验轴承声发射信号添加白噪声的标准差为原始信号标准差的0.2倍，迭代次数为100。图2为滚动体2 mm线缺陷轴承的AE信号EEMD分解图。分解的各分量频带依次从高频到低频分布，由于轴承故障声发射信号主要处在高频段，图2只列出了前7个IMF分解结果。并对滚动体2 mm 线缺陷轴承进行CEEMD分解，得到11个IMF分量和一个残余量，图3为滚动体2 mm线缺陷轴承经过CEEMD分解的前7个IMF分量。

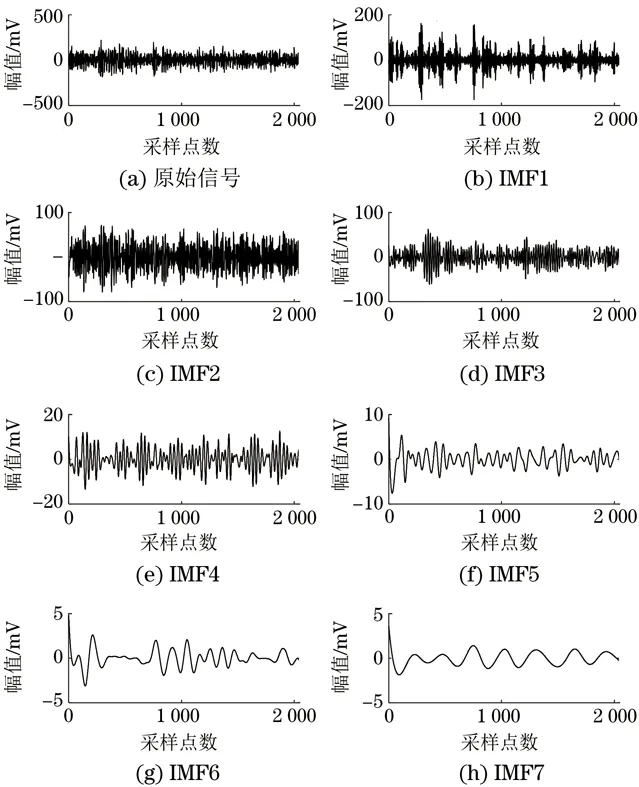
图2 滚动体2 mm线缺陷轴承的AE信号EEMD分解图

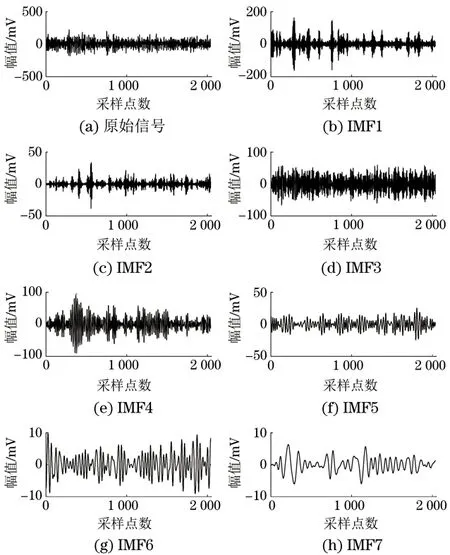
图3 滚动体2 mm线缺陷轴承的AE信号CEEMD分解图

比较图2和图3中的IMF1分量可以看出，尽管幅值范围相同，但经CEEMD分解的IMF1分量对于模态混叠程度较轻，并且图2中的IMF2分量包含了图3中的IMF2和IMF3两个分量，也就是说EEMD算法未能完全消除模态混叠现象，而将尺度相近的两个分量分解到一个分量中。由此可以看出相比EEMD分解，CEEMD算法对于低速轴承声发射信号拥有更优良的抗模态混叠性能。

4.1有效IMF分量的筛选

尽管CEEMD分解能够基本消除模态混叠问题，但CEEMD分解有可能存在过度分解等原因使分解的IMF分量中仍然存在虚假分量，从而对于低速轴承的故障诊断结果出现偏差。因此，提出将IMF分量与原信号的互相关系数和方差贡献率相结合的方式，对轴承声发射信号经过CEEMD分解的IMF分量进行筛选。方差体现了轴承声发射信号的波动特征，因而通过计算方差贡献率能够筛选出含有主要脉冲信号的有效IMF分量。对于原始信号x(t)的方差贡献率定义为

式中：E，s2分别为轴承声发射信号数据序列的均值和方差；m为采样时间t内采集一个声发射波形的序列数。

由于轴承声发射信号分解后的IMF分量含有不同的故障脉冲信息，故IMF分量计算的方差贡献率不同，因而通过计算方差贡献率筛选含有主要故障特征的IMF分量是可行的。为验证该方法，分别求出了无缺陷、外圈缺陷、滚动体缺陷轴承经过CEEMD分解的IMF分量方差贡献率(见图4)。并且在图4中,将方差贡献率法和互相关系数法提取出的有效IMF分量进行了对比。

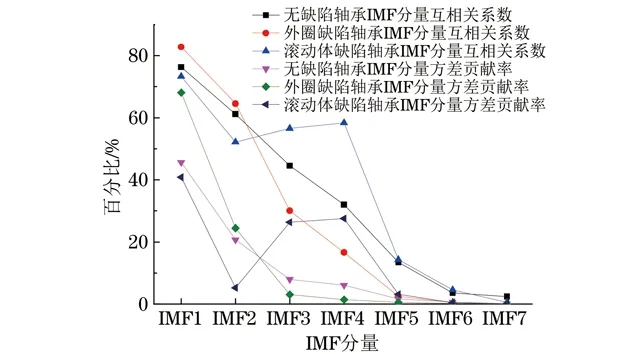
图4 不同故障轴承IMF分量与原信号的互相关系数和方差贡献率

从图中可以看出，将原信号经CEEMD分解后的特征信息主要集中在前四阶分量中，可以结合前四阶分量对信号进行重构。当轴承存在外圈缺陷时，IMF1分量和IMF2分量的方差贡献率和互相关系数比无缺陷时的高，说明外圈主要故障信息集中在IMF1和IMF2分量中；当滚动体存在缺陷时，IMF3和IMF4分量的方差贡献率和互相关系数要比无缺陷时高，说明滚动体主要的故障信息集中在IMF3和IMF4中。并且比较互相关系数法和方差贡献率法，对于筛选含有轴承主要故障信息的IMF分量，后者优势更大。从以上分析结果可以得出， CEEMD分解方法可以用于低速轴承的故障诊断，将方差贡献率和互相关系数法相结合对于轴承故障特征的提取将更加准确。

4.2基于CEEMD能量熵和SVM的轴承故障诊断

结合上述分析，分别计算无缺陷、滚动体缺陷和外圈缺陷轴承前四阶IMF分量的能量熵值。并将其作为特征向量输入到支持向量机对不同故障轴承进行分类识别。该方法的实现流程如图5所示。

图5 基于CEEMD能量熵和SVM低速轴承故障诊断流程图

将不同故障类型的轴承在试验台上低速运转，分别采集无缺陷、滚动体缺陷、外圈缺陷状态下的声发射信号作为数据样本，对每种类型轴承采集60组声发射信号样本；并将前30组作为训练样本，其余的作为测试样本。将不同故障类型轴承声发射信号进行CEEMD分解，得到若干IMF分量，通过方差贡献率和互相关系数筛选有效分量，对筛选的前四阶IMF分量分别计算能量熵，表1列出了每种状态下声发射信号有效分量的部分能量熵。将30组声发射数据样本能量熵作为特征向量，输入到多分类支持向量机中进行训练。同样，对后30组声发射数据样本计算出有效分量的能量熵，将其作为特征向量输入到已经训练好的支持向量机进行模式识别。试验支持向量机选用的核函数为径向基(RBF)核函数，结合文献[16]对RBF核函数参数的优化方法[16]和多次试验，所采用的RBF核函数的最佳惩罚系数c=0.031 3，核参数g=4。此外还选取了一些常用的分类识别方法作为比较对象，其分类识别结果如表2所示。从表2可以看出，笔者提出的方法相比其他方法具有更高的分类识别准确率。比较支持向量机和BP神经网络，针对低速轴承小样本数据，SVM的分类识别效果比BP神经网络高；并且将EEMD分解和CEEMD分解的有效分量能量熵分别作为特征向量输入到SVM中对比分析得知，将CEEMD能量熵作为特征对于低速轴承的分类识别率更高。说明CEEMD方法对于低速轴承声发射信号的故障特征提取更加准确。综上所述，可将CEEMD能量熵和SVM相结合用于低速轴承的损伤状态监测和故障类型的识别。

表1 低速轴承不同故障状态下的有效IMF能量熵

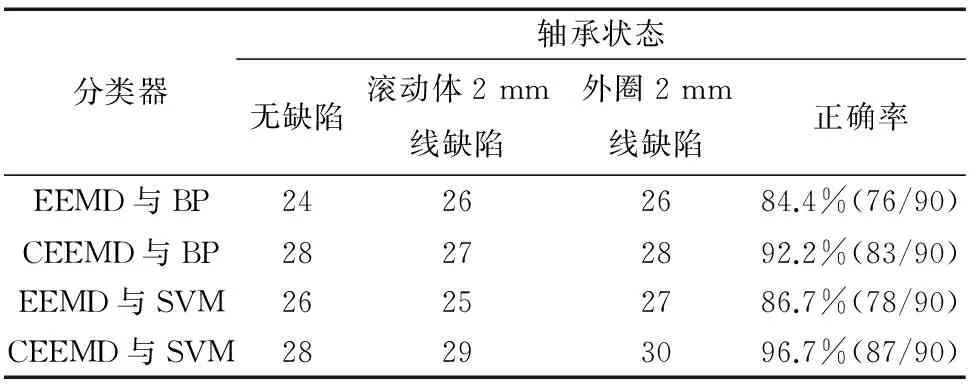
表2 分类识别结果比较

5 结论

(1) 将CEEMD方法应用于低速轴承声发射信号分解，其模态混叠效应比EEMD分解程度轻，通过CEEMD分解后筛选的有效分量能量熵更能反映低速轴承的损伤状态变化。

(2) 结合IMF分量的方差贡献率和互相关系数筛选的有效分量更加准确，并且将CEEMD能量熵和SVM相结合可以对低速轴承的损伤状态和故障类型进行识别。

(3) 将EEMD各分量能量熵和CEEMD各分量能量熵分别用于SVM和BP神经网络中识别不同故障类型的轴承。结果表明，对于小样本数据，SVM比神经网络具有更大的优势，准确率也较高，CEEMD能量熵反映低速轴承的损伤状态比EEMD能量熵的效果更佳。

[1] 钟秉林，黄仁.机械故障诊断学[M]. 北京：机械工业出版社，2007.

[2] RAY A G. Monitoring rolling contact bearings under adverse conditions[C]// IMechE Conference on Bibrations in Rotating Machinery.[S.l.]:[s.n], 1980, 187-194.

[3] Al-GHAMD A M, MBA D A.Comparative experimental study on the use of acoustic emission and vibration analysis for bearing defect identification and estimation of defect size[J]. Mechanical Systems and Signal Processing, 2006, 20(7):1537-1571.

[4] MBA D, RAJ B K N, RAO. Development of acoustic emission technology for condition monitoring and diagnosis of rotating machines: bearings, pumps, gearboxes, engines and rotating structures[J]. The Shock and Vibration Digest, 2006, 38(1):3-16.

[5] 耿容生，沈功田，刘时风. 声发射信号处理和分析技术[J]. 无损检测，2002,24(1):23-28.

[6] 郝如江，卢文秀，褚福磊. 声发射检测技术用于滚动轴承故障诊断的研究综述[J]. 振动与冲击, 2008, 27(3):75-79.

[7] 赵一帆，齐明侠，赵继红，等.基于声发射技术的滚动轴承故障检测[J]. 轴承，2010(4)：50-53.

[8] 孙永生，李猛，刘恒，等.基于声发射检测技术的滚动轴承缺陷检测[J]. 无损检测，2015，37(8):17-20.

[9] LEI Yaguo, HE Zhengjia, ZI Yanyang. Application of an intelligent classification method to mechanical fault diagnosis[J]. Expert Systems with Applications, 2009,36(6):9941-9948.

[10] SMITH S J. The local mean decomposition and its application to EEG perception data[J]. Journal of the Royal Society Interface,2005,2(5):443-454.

[11] WU Z H, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1):1-41.

[12] 陈隽,李想. 运用总体经验模式分解的疲劳信号降噪方法[J].振动、测试与诊断,2011,31(1):15-19.

[13] YEH J R,HUANG N E. Complementary ensemble empirical mode decomposition: a novel noise enhanced data analysis method[J]. Advances in Adaptive Data Analysis, 2010, 2(2):135-156.

[14] CORTES C, VAPNIK V. Support-vector networks[J]. Machine Learning, 1995, 20(3):273-297.

[15] CHANG C C, LIN C J, LIBSVM. A library for support vector machines[J]. ACM Transactions on Intelligent Systems and Technology,2011,2(3):1-27.

[16] 奉国和. SVM分类核函数及参数选择比较[J]. 计算机工程与应用，2011,47(3):123-125.

AcousticEmissionDiagnosisofLow-SpeedBearingFaultsBasedonCEEMDEnergyEntropyandSVM

YANG Jie, ZHANG Penglin, LIU Zhitao, CHANG Hai

(State Key Laboratory of Advanced Processing and Recycling of Nonferrous Metals,Lanzhou University of Technology, Lanzhou 730050, China)

Aiming at the problem of fault diagnosis of low-speed bearing, an acoustic emission diagnosis method based on the combination of complementary ensemble empirical mode decomposition (CEEMD) energy entropy and support vector machine (SVM) is proposed. Firstly, the acoustic emission signals of bearing with different damage states are decomposed by CEEMD, thus an adaptive intrinsic mode component (IMF) is obtained. Afterwards, the combination of the variance contribution rate and IMF component mutual correlation coefficient is used to remove the false component and to sift out effective component for signal reconstruction. Due to the different energy distributions of different damage bearing, the damage state of the bearing can be characterized by the change of energy entropy. The energy entropy of the extracted effective IMF components is calculated as the feature vector of different fault bearing. The feature vector is input to the support vector machine to classify and identify the different faults. The experimental results show that the correlation coefficient and variance contribution rate can be selected with the main fault information of the IMF component. At the same time, it is proven that SVM is better than BP neural network in identifying different fault types of low speed bearings.

acoustic emission; low-speed bearing; CEEMD; energy entropy; SVM; fault diagnosis

TG17；TH133；TG115.28

： A

：1000-6656(2017)09-0001-06

2017-04-04

杨 杰(1993-)，男，硕士研究生，主要研究方向为无损检测新技术，低速轴承故障诊断

张鹏林，13919112896@163com

10.11973/wsjc201709001