基于I-V下垂控制的直流微电网动态特性分析与改善

王皓界， 韩民晓， Josep M.Guerrero

(1. 华北电力大学电气与电子工程学院， 北京 102206; 2. 奥尔堡大学能源技术系， 丹麦 奥尔堡 9220)

基于I-V下垂控制的直流微电网动态特性分析与改善

王皓界1， 韩民晓1， Josep M.Guerrero2

(1. 华北电力大学电气与电子工程学院， 北京 102206; 2. 奥尔堡大学能源技术系， 丹麦 奥尔堡 9220)

本文对孤立直流微电网动态特性进行了分析,并提出了改善策略。在孤网条件下，电压主要靠系统中基于储能的DC/DC变换器进行控制，因此多DC/DC变换器动态特性即可反应系统全局的动态特性。本文中各DC/DC变换器采用I-V下垂控制，并以负载的变化量为输入，变换器输出电流、占空比及母线电压为状态变量对多DC/DC变换器进行了大信号模型的建立。基于上述模型，本文对输出电流动态特性的影响因素进行了根轨迹分析，最后提出自适应P控制策略以提高直流微电网中的动态特性。最后通过仿真对提出的模型及控制策略进行了验证。

直流微电网； 动态特性； 多DC/DC变换器； 大信号模型； 自适应P控制

1 引言

直流微电网有利于分布式电源的接入，因而受到广泛的关注。随着直流微电网容量的扩大，储能容量也会随之增加，储能电池往往需要通过多DC/DC变换器与直流母线相连[1-4]。除此之外，不同电压等级的母线也需要通过多DC/DC变换器相连，因此多变换器的协调控制策略成为直流微电网的关键性技术之一[5,6]。

下垂控制利用虚拟阻抗，能够使各变换器按照虚拟阻抗的倒数为比例分配负载电流。目前绝大部分文献的研究工作主要集中在V-I下垂控制，其下垂特性随着电流增大来减小直流母线电压参考值，从而实现各变换器的电流分配[7]，但现有文献对I-V下垂控制的研究较少[8]，相关研究也主要集中在上层控制优化，如消除线路阻抗引起的环流[9-11]、电压偏差补偿[12]、电池管理[13,14]及效率优化[15,16]等，对于多DC/DC变换器动态特性研究较少。文献[17]针对交流微电网中的下垂控制策略建立了小信号模型，并利用根轨迹法对其动态特性进行研究。文献[18]对基于光伏电池的变换器动态特性进行了研究。文献[19]针对三相交错DC/DC变换器提出了前馈控制策略，在动态过程中提高内环电流参考值从而改善其动态特性，减少电压跌落，但是该控制策略只针对单台DC/DC变换器。

直流微电网中的分布式电源一般为最大功率跟踪(MPPT)控制，在本文中可被视为不可控的功率源负载。在孤网条件下，当直流微电网中的负载发生变化时，储能电池主要承担系统的电压控制任务，因此基于储能的DC/DC变换器动态特性能够决定整个系统的动态特性。为了分析其动态特性，首先需要对多DC/DC变换器进行建模。在各类变换器建模方法中，平均值建模方法可有效地应用在DC/DC变换器的大信号模型建立中，使模型中各个变量之间的关系线性化[20-25]。本文基于平均值建模思想，以负载为输入，变换器电压、占空比及直流母线电流为状态变量，对基于I-V控制的多DC/DC变换器进行了建模，并对输入部分的建模方案进行了对比与分析。仿真结果表明，本文推导的模型可以准确反映负载变化对系统动态特性的影响。基于本文模型，利用根轨迹法，对多变换器动态特性的影响因素进行了分析，进而提出了自适应P控制策略以改善多变换器的动态特性。仿真结果验证了自适应P控制策略的有效性。

2 多变换器建模

2.1I-V下垂控制

典型的直流微电网架构如图1所示。当系统中存在多套储能设备并通过并联的DC/DC变换器与直流母线相连时，利用下垂控制可以按照规定比例实现各变换器功率分配。I-V下垂控制框图如图2所示，其中u为直流母线电压，iref为下垂特性输出的参考电流，i为DC/DC变换器电感平均电流即输出电流，Urate为直流母线额定电压，r为虚拟阻抗。由图2可知，I-V下垂控制通过在直流母线电压下降时增加参考电流值实现，其下垂特性可表示为：

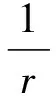
(1)

设系统中的变换器数量为n，则各变换器可根据虚拟阻抗分配输出功率，即

i1r1=i2r2=…=inrn

(2)

式中，ik,rk(k=1, 2, …,n)分别为变换器k的输出电流和虚拟阻抗。

图1 直流微电网架构Fig.1 DC microgrid architecture

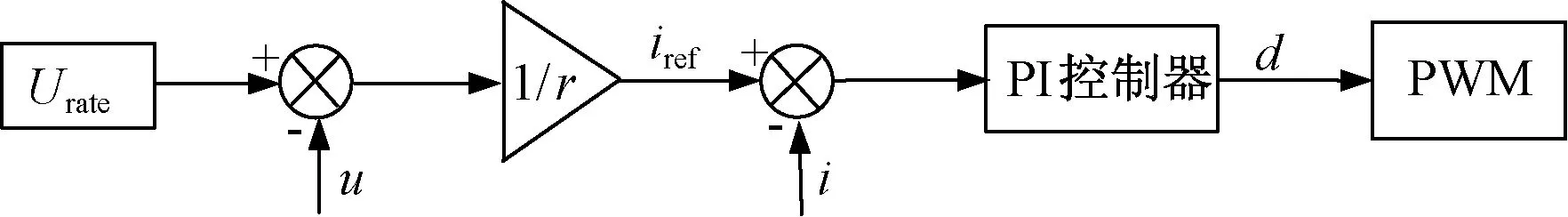
图2 I-V下垂控制Fig.2 I-V droop control

2.2大信号模型

设L为DC/DC变换器输出侧电感，T为变换器开关周期，d为其任意时刻的占空比，Uin为电池电压，u为直流母线电压，则电感电流平均值在一个周期的增量Δicycle为：

(3)

在稳定状态下，设直流母线电压为u0；Iref0、I0、D0分别为各变换器初始参考电流、输出电流及占空比，不难得到Iref0=I0，其中

负载发生变化时，设直流母线变化量为ud(t)；Idref(t)、Id(t)、Dd(t) 分别为各变换器的参考电流、输出电流及占空比的变化量，其中

设I为各元素全为1的n阶向量，负载电流发生变化的时刻为0时刻。由式(3)可以得到各变换器输出电流的变化量为：

(4)

式中

由式(3)可知，在稳定状态下，有

ITu0=UinD0T

(5)

将式(5)代入式(4)，并在等式两边同时求导及转置，可以得到：

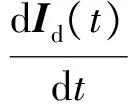
(6)

作为功率平衡的重要部分，建模过程中需要对系统中负载进行简化，只有将负载的变化量作为状态空间模型的输入，变换器输出电流及母线电压作为状态变量，才能分析负载变化对电流、电压动态过程的影响。

首先考虑传统的纯电阻负载这一情况，设系统中电阻的初始负载阻值为rld0，负载变化时，等效阻值变化量为rldv(t)，则不难得到：

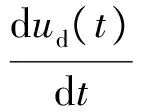
(7)

式中，C为直流母线等效电容值。式(7)中，电阻阻值与电压表现出非线性关系，且初始负载阻值rld0无法消除，所以无法将负载阻值变化量作为输入、变换器输出电流及母线电压作为状态变量进行建模。

若将负载视为纯功率源，设系统中负载的初始功率为Pld0，负载变化量为Pldv(t)，则式(7)可改写为：

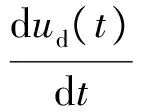
(8)

不难得到式(8)与式(7)情况类似，无法用于建立状态空间模型。

若将负载视为电流源，设负载的初始电流为ild0，变化量为ildv(t)，则不难得到式(9)：

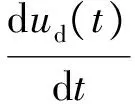
(9)

可以看出，若将负载变化视为负载电流变化，则负载电流变化量与所有状态变量呈线性关系。在直流微电网中，纯电阻负载和功率源性负载往往并存，当直流母线电压波动时，两种负载的负载电流会向不同的方向变化。以母线电压升高为例，纯电阻负载的电流会随之升高，而功率源性负载的电流会随之降低，总电流变化量会得到一定的抵消。再考虑正常情况下，母线电压波动较小，因此将系统中的负载变化用负载电流变化表示不但有利于建模进行动态特性分析，且更加符合实际情况。综上所述，本文用负载电流变化量作为状态空间模型的输入量来研究负载变化对电流、电压动态过程的影响。由电流内环为PI控制可以得到：

(10)

式中，Kpi、Kii分别为各变换器的比例系数及积分系数组成的对角矩阵，即

由式(1)不难得到：

(11)

式中，R代表各变换器虚拟阻抗组成的对角矩阵，即

将式(11)代入式(10)并求导，可得：

(12)

将式(6)、式(9)代入式(12)，可以得到：

(13)

由式(6)、式(9)、式(13)可以得到多DC/DC变换器的状态空间模型如下：

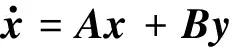
(14)

式中

y=ildv(t)

该状态空间模型中，每个变换器都有输出电流和占空比两个独立的状态变量，所有变换器共享母线电压状态变量。因此，当一个系统中的变换器数量为n时，其状态变量的总数量为2n+1。

2.3模型验证

本文利用仿真软件PSCAD/EMTDC对2.2节状态空间模型进行了仿真验证。设系统中的变换器数量为4，仿真参数如表1所示。

表1 仿真参数Tab.1 Simulation parameters

改变各变换器PI参数，分别对本文提出的模型以及PSCAD/EMTDC仿真进行阶跃响应测试。不同PI参数下电压及电流阶跃响应曲线如图3所示。由图3可知，本文提出的状态空间模型阶跃响应与仿真结果完全一致。因此，可利用该模型对直流微电网中多变换器的动态特性进行分析。

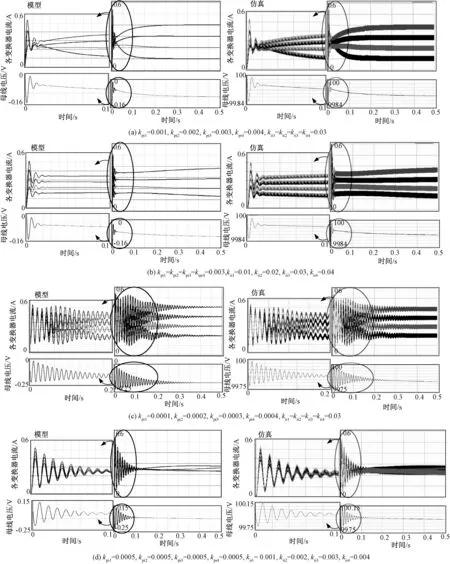
图3 阶跃响应测试Fig.3 Tests of current step respond

3 动态特性分析

基于本文提出的状态空间模型，本节以4台变换器为例，分别以电流内环比例参数和积分参数为变化量，对输出电流动态特性进行根轨迹分析。

3.1比例参数的影响

设4台变换器电流内环的积分参数为0.01，比例参数初始值为0.001，分别将变换器1、变换器4以及所有变换器的比例参数由0.00001增大到0.1，所有变换器输出电流与负载电流传递函数的极点变化趋势如图4所示。

图4 比例参数变化时的轨迹图Fig.4 Root locus analysis with proportional terms changing

由图4(a)和图4(b)可知，任意一台变换器的比例参数会影响系统中所有变换器的动态特性，且变换器虚拟阻抗越小，对整个系统的影响越大。由图4(a)～图4(c)可知，与任意单台变换器的比例参数增大相比，多台变换器的比例参数同时增大对系统动态特性的影响会更加剧烈。由图4还可看出，比例参数的增大会抑制变换器输出电流在动态过程中的振荡，并且在动态过程的前期更加快速缩小输出电流误差，但是在动态过程后期会降低消除误差的速度。除此之外，由图4(c)可知，当所有变换器的比例参数过小时，可能会使系统失去稳定性。

3.2积分参数的影响

设4台变换器电流内环的比例参数为0.001，积分参数初始值为0.01，分别将变换器1、变换器4以及所有变换器的积分参数由0.0001增大到1，所有变换器输出电流与负载电流传递函数的极点变化趋势如图5所示。

图5 积分参数变化时的轨迹图Fig.5 Root locus analysis with integral terms changing

由图5(a)和图5(b)可知，任意一台变换器的积分参数会影响系统中所有变换器的动态特性，且变换器虚拟阻抗越小，对整个系统的影响越大。由图5(a)～图5(c)可以看出，多台变换器的积分参数同时增大对系统动态特性的影响会更加剧烈。除此之外，对比图4与图5可知，改变比例参数对极点影响相对较大，改变积分参数对极点变化的影响相对较小。由图5还可以看出，积分参数的增大会促进变换器输出电流在动态过程中的振荡，但同时可以增加消除误差的速度。其中，由图5(c)可知，当所有变换器的积分参数过大时，可能会导致系统失去稳定性。

4 自适应P控制

4.1控制原理

由第3节分析可知，当积分参数过大容易引起振荡，过小将降低稳态误差的消除速度，因此对积分参数的调节很难在不引起振荡的情况下提高变换器响应速度。而增大比例参数P会在动态过程前期加快误差的减小速度且抑制振荡，较小的P参数更加有利于误差的完全消除，但是较大的P参数会导致变换器输出电流在稳态时发生波动，因此为了在保证系统稳态特性的同时改善其动态特性，本节提出自适应P控制，在动态过程前期利用较大的P参数快速缩小误差，在后期减小P参数快速消除误差并保证输出电流的稳态特性。

设ek(t)为变换器k的参考电流与输出电流的绝对误差，即

(15)

在稳态下ek(t)为0，但是在动态过程中ek(t)会增大。当ek(t)增大到相应阈值，则增大P参数从而快速缩小输出电流误差。设Δumax为稳态下直流母线纹波的最大幅值，Δimaxk为输出电流纹波的最大幅值，为了保证比例参数在稳态下保持恒定，相应阈值e1k应该满足：

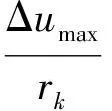
(16)

为了防止在阈值附近P参数的频繁切换，需要加入滞环控制，如式(17)所示：

(17)

式中，Δkpk为P参数的变化量；kpok为动态过程前期Δkpk的增量。当ek(t)增长至e2k，则Δkpk变为kpok从而提高动态过程前期的响应速度；当ek(t)减小至e1k，则Δkpk回到0从而在动态过程后期快速消除稳态误差。因此，由式(2)可以得到各变换器阈值的关系如下：

(18)

当ek(t)减小至e1k时，误差虽然大幅减小但仍未被完全消除，此时Δkpk减小到0将导致PI控制器输出的占空比向相反方向变化，进而导致输出电流向相反方向变化，这将使输出电流误差再次增大，Δkpk再次变为kpok。Δkpk的反复变化会导致输出电流的剧烈波动，影响系统的稳定，使动态特性更差。为了避免这个问题，本文在PI控制器输出端加入了前馈补偿，在Δkpk下降沿瞬间保持PI控制器输出的占空比不变，以改善自适应P控制引起的电流波动问题。在Δkpk下降沿瞬间，占空比补偿值dcpk为：

dcpk=kpok[idrefk(t)-idk(t)]

(19)

由此可以得到自适应P控制的整体框图，如图6所示。

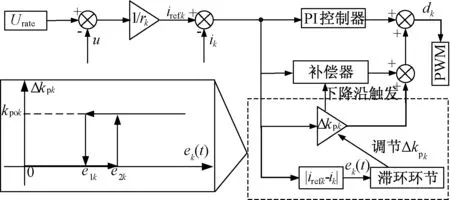
图6 自适应P控制Fig.6 Adaptive P-control

4.2仿真验证

本文以4台变换器为例，利用仿真软件PSCAD/EMTDC对自适应P控制策略进行了仿真验证，仿真参数如表1所示。所有变换器的比例参数设为0.001，积分参数设为0.01，在3s时刻突加1kW负载，4台变换器输出电流及直流母线电压如图7所示。

图7 不使用自适应P控制的仿真波形Fig.7 Simulation waveform without adaptive P-control

可以看出，在动态过程前期4路输出电流及直流母线电压会出现短暂的高频振荡，且4路电流在动态过程中的均流效果较差，恢复时间较长。采用自适应P控制策略，PI控制器输出端没有占空比补偿，则4路电流及直流母线电压如图8所示。可以看出，比例参数反复变化引起了电流及电压波动，且电流及电压恢复时间没有得到改善。采用含占空比补偿项的自适应P控制，其电流及电压波形如图9所示，在动态过程前期由于比例参数较大，对高频振荡起到了很好的抑制作用，且4路电流在动态过程中的均流效果明显好于图8所示电流，其恢复时间也明显得到改善。

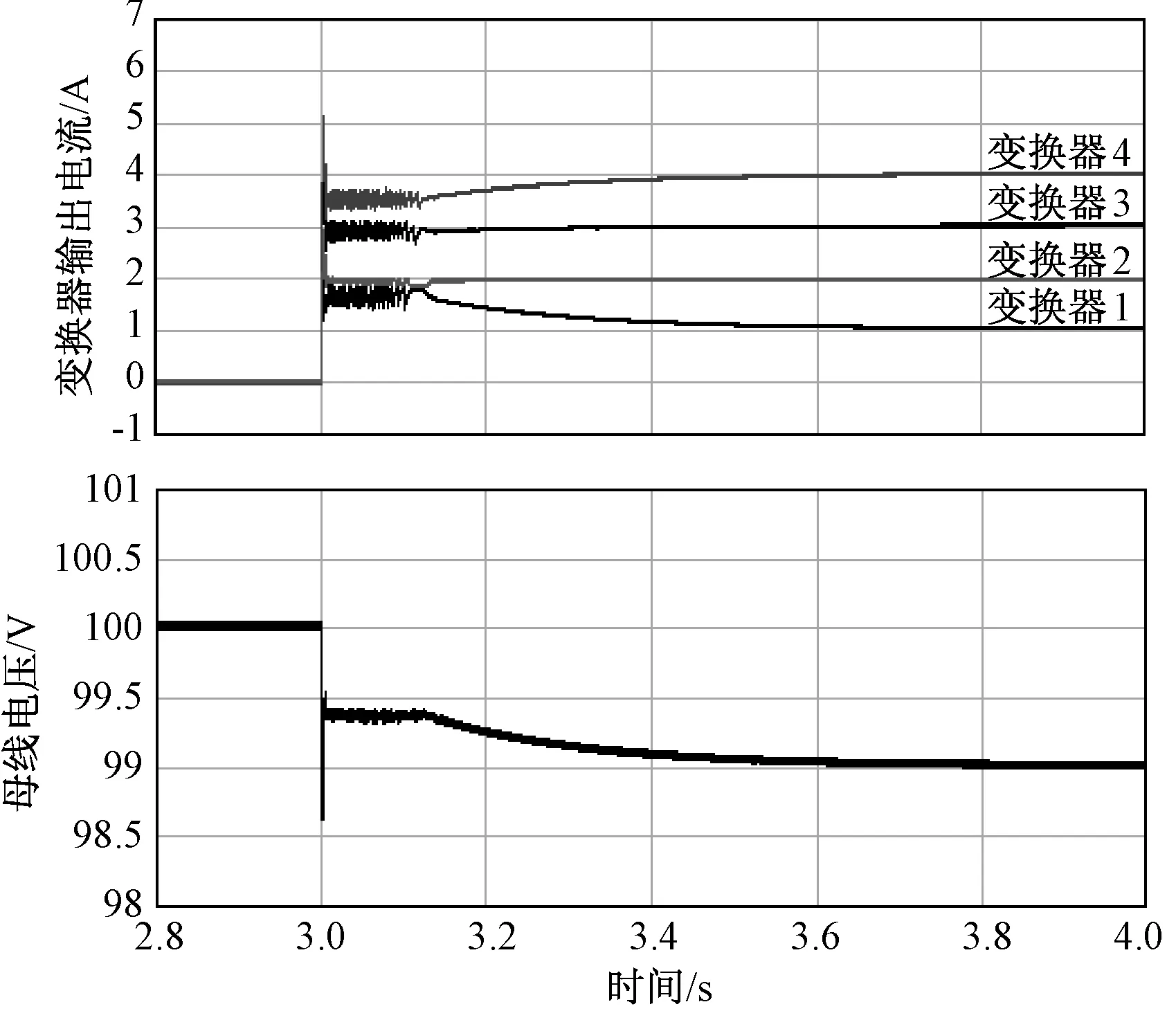
图8 无占空比补偿的自适应P控制仿真波形Fig.8 Simulation waveform of adaptive P-control without duty ratio compensation

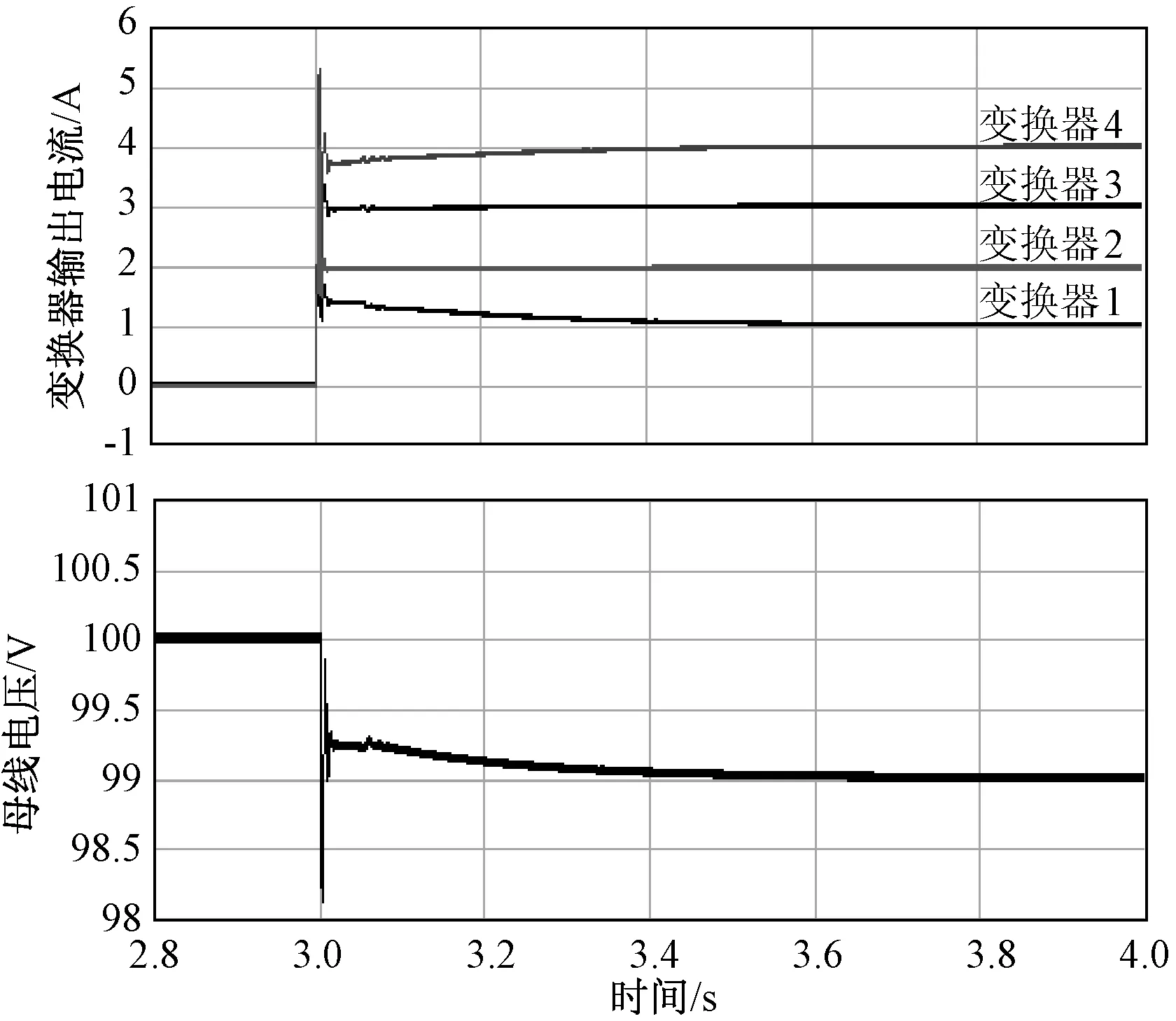
图9 含占空比补偿的自适应P控制仿真波形Fig.9 Simulation waveform of adaptive P-control with duty ratio compensation

5 结论

本文针对直流微电网中的多DC/DC变换器进行了状态空间模型的建立，在此基础上进行了动态特性的分析，提出了改善动态特性的自适应P控制策略，具体结论如下：

(1)将负载电流作为模型的输入量，变换器输出电流、占空比及直流母线电压作为状态变量，建立状态空间平均值模型，其可以有效反效负载变化对直流系统的影响情况，仿真结果验证了模型的准确性。

(2)基于本文模型，由根轨迹分析可知，在动态过程中，大的内环比例参数有利于动态过程前期的误差减小，且对电流及电压振荡有很好的抑制作用，后期采用较小的比例参数可促进稳态误差的消除；而大的积分参数有利于更快地消除误差，但会加剧电压和电流振荡，因此积分参数不宜过大或过小。

(3)本文提出了自适应P控制策略，通过动态调节比例参数改善系统的动态过程，其中需要在内环PI控制器输出端增加占空比补偿项，抵消比例参数变化引起的电流振荡。通过仿真验证了该控制策略。

[1] 韩民晓, 王皓界(Han Minxiao, Wang Haojie). 直流微电网——未来供用电领域的重要模式(DC micro-grid——The important mode in the field of power supply and consumption)[J]. 电气工程学报(Journal of Electrical Engineering), 2015, 10(5): 1-9.

[2] 丛晶, 宋坤, 鲁海威, 等(Cong Jing, Song Kun, Lu Haiwei, et al.). 新能源电力系统中的储能技术研究综述(Review of energy storage technology for new energy power system)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2014, 33(3): 53-59.

[3] 朱永强, 贾利虎, 王银顺(Zhu Yongqiang, Jia Lihu, Wang Yinshun). 微电网结构设计的基本原则(Basic design principles for micro-grid architecture)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2015, 34(9): 44-49.

[4] 杜少飞, 谢文超, 朱永强, 等(Du Shaofei, Xie Wenchao, Zhu Yongqiang, et al.). 并网型直流微电网主动协调控制方法研究(Research on active coordination control method for grid-connected DC microgrid)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2017, 36(6): 30-38.

[5] 吴卫民，何远彬，耿攀，等(Wu Weimin，He Yuanbin，Geng Pan，et al.)．直流微网研究中的关键技术(Key technologies for DC micro-grids)[J]．电工技术学报(Transactions of China Electrotechnical Society)，2012，27(1)：98-106．

[6] 蔡冰倩, 贾利虎, 朱永强, 等(Cai Bingqian, Jia Lihu, Zhu Yongqiang, et al.). 直流微电网电压等级序列选择的影响因素研究(Research on influence factor of voltage class series option in DC microgrid)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2016, 35(12): 45-51.

[7] Fu Y, Zhang Z, Wang Y, et al. Research on power coordinated control strategy of wind turbine-based DC microgrid under various modes[A]. 8th IEEE Power Electronics and Motion Control Conference[C]. Hefei, China, 2016. 1480-1484．

[8] 王毅, 张丽荣, 李和明, 等(Wang Yi, Zhang Lirong, Li Heming, et al.). 风电直流微网的电压分层协调控制(Hierarchical coordinated control of wind turbine-based DC microgrid)[J]. 中国电机工程学报(Proceedings of the CSEE), 2013, 33(4): 16-24．

[9] Lu X, Guerrero J M, Sun K, et al. An improved droop control method for DC microgrids based on low bandwidth communication with DC bus voltage restoration and enhanced current sharing accuracy[J]. IEEE Transactions on Power Electronics, 2013, 29(4): 1800-1812．

[10] Zhong Q. Robust droop controller for accurate proportional load sharing among inverters operated in parallel[J]. IEEE Transactions on Industrial Electronics, 2011, 60(4): 1281-1290．

[11] Anand S, Fernandes B G, Guerrero J. Distributed control to ensure proportional load sharing and improve voltage regulation in low-voltage DC microgrids[J]. IEEE Transactions on Power Electronics, 2012, 28(4): 1900-1913．

[12] Meng L, Dragicevic T, Roldán-Pérez J, et al. Modeling and sensitivity study of consensus algorithm-based distributed hierarchical control for DC microgrids[J]. IEEE Transactions on Smart Grid, 2016, 7(3): 1504-1515．

[14] Lu X, Sun K, Guerrero J M, et al. Double-quadrant state-of-charge-based droop control method for distributed energy storage systems in autonomous DC microgrids[J]. IEEE Transactions on Smart Grid, 2014, 6(1): 147-157．

[15] 王皓界，韩民晓，Josep M Guerrero，等(Wang Haojie, Han Minxiao, Josep M Guerrero, et al.).基于自律分散系统的直流微电网稳定控制器优化设计(Optimization design of DC micro-grid stability controller based on the autonomous decentralized system)[J]. 中国电机工程学报(Proceedings of the CSEE)，2016，36(2)：360-367．

[16] Meng L, Dragicevic T, Vasquez J C, et al. Tertiary and secondary control levels for efficiency optimization and system damping in droop controlled DC-DC converters[J]. IEEE Transactions on Smart Grid, 2015, 6(6): 2615-2626．

[17] Yu K, Ai Q, Wang S, et al. Analysis and optimization of droop controller for microgrid system based on small-signal dynamic model[J]. IEEE Transactions on Smart Grid, 2016, 7(2): 695-705.

[18] Leppäaho J, Suntio T. Dynamic characteristics of current-fed superbuck converter[J]. IEEE Transactions on Power Electronics, 26(1): 200-209．

[19] Wang H, Han M, Yan W, et al. A feed-forward control realizing fast response for three-branch interleaved DC-DC converter in DC microgrid[J]. Energies, 2016, 9(7): 529．

[20] Oraw B, Ayyanar R. Large signal average model for an extended duty ratio and conventional Buck[A]. INTELEC 2008 - 2008 IEEE 30th International Telecommunication Energy Conference[C]. 2008. 1-8．

[21] Chiniforoosh S, Jatskevich J, Yazdani A, et al. Definitions and applications of dynamic average models for analysis of power systems[J]. IEEE Transactions on Power Delivery, 2010, 25(4): 2655-2669.

[22] Vorpérian V. Simplified analysis of PWM converters using model of PWM switch-II: Discontinuous conduction mode[J]. IEEE Transactions on Aerospace and Electronic systems, 1990, 26(3): 497-505.

[23] Nirgude G, Tirumala R, Mohan N. A new, large-signal average model for single-switch DC-DC converters operating in both CCM and DCM[A]. 2001 IEEE 32nd Annual Power Electronics Specialists Conference[C]. 2001. 3: 1736-1741.

[24] Sun J. Unified averaged switch models for stability analysis of large distributed power systems[A]. Fifteenth Annual IEEE Applied Power Electronics Conference and Exposition[C]. 2000. 1: 249-255.

[25] Pavlovic T, Bjazic T, Ban Z. Simplified averaged models of DC-DC power converters suitable for controller design and microgrid simulation[J]. IEEE Transactions on Power Electronics, 2013, 28(7): 3266-3275.

AnalysisandimprovementofDCmicrogriddynamicperformancebasedonI-Vdroopcontrol

WANG Hao-jie1, HAN Min-xiao1, Josep M. Guerrero2

(1. School of Electric and Electronic Engineering, North China Electric Power University, Beijing 102206, China; 2. Department of Energy Technology, Aalborg University, Aalborg 9220, Denmark)

The dynamic performance of DC microgrid has been analyzed and improved by this paper. In an islanded system, the bus voltage is controlled by paralleled DC/DC converters based on the energy storages, so the dynamic performance of the paralleled converters can reflect the dynamic of the system. In this paper, the I-V droop control method is used for the paralleled converters. The large signal model is built. In this model, the input is the load variation and the state variables are converters’ output currents, duty ratios and the bus voltage. Based on this model, the root locus method is used to analyze the dynamic performance of the converters’ output current. Thus, the adaptive P control method is proposed to improve the dynamic performance of the DC microgrid. The simulation has been conducted to verify the proposed model and the control method.

DC microgrid; dynamic performance; paralleled DC/DC converters; large signal model; adaptive P control

2017-04-21

国家电网公司科技项目 (PDB17201600116)

王皓界(1989-)， 男， 河南籍， 博士研究生， 研究方向为直流微电网； 韩民晓(1963-)， 男， 陕西籍， 教授， 博导， 博士， 研究方向为电力电子在电力系统中的应用。

10.12067/ATEEE1704071

： 1003-3076(2017)09-0080-09

： TM71