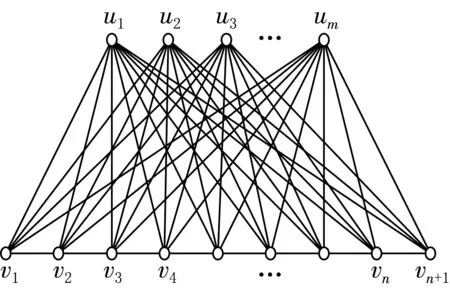
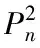两类图及其冠的优美标号

唐保祥，任 韩

(1.天水师范学院数学与统计学院，甘肃 天水 741001； 2.华东师范大学数学系，上海 200062)

·研究简报·

两类图及其冠的优美标号

唐保祥1，任 韩2

(1.天水师范学院数学与统计学院，甘肃 天水 741001； 2.华东师范大学数学系，上海 200062)

用构造法对两类图和两类图的冠的优美性进行了研究，得到了如下结论：对任意正整数m和n，设Em和Pn分别是m个顶点的空图和有n+1个顶点的路，那么完全3部图K1，m，n，I(K1，m，2)，联图Em∨Pn和I(E2∨P2n)都是优美图.

路；联图；空图；冠；优美图

1 预备知识

优美图的研究理论已有广泛应用，但是目前没有系统理论对一般图的优美性进行研究.[1-12]马克杰教授在文献[1]中提出猜想：所有优美图的冠都是优美图.这一猜想至今没有被证明或否定.若这个猜想正确，那么优美图的冠都是优美图，于是就有很多图类被证明是优美图，这将是一个很有意义的结论.对任何正整数m和n，本文用构造的方法给出了图K1，m，n，I(K1，m，2)，联图Em∨Pn和I(E2∨P2n)的优美标号，从而证明了这四类图都是优美图.

定义1[1]图G的每个顶点上都粘接1条悬挂边得到的图，称为图G的冠，记作I(G).

定义2[1]设图G=(V，E).若存在单射θ：V(G)→{0，1，2，…，|E(G)|}，使得∀e=uv∈E(G)，由θ′(e)=|θ(u)-θ(v)|导出双射θ′：E(G)→{1，2，…，|E(G)|}，则称图G是优美图，θ称为图G的一个优美标号，θ′称为由θ导出的边标号.

2 主要结果及其证明

定理1 ∀m，n∈Z+，完全3部图K1，m，n是优美图.

证明显然|E(K1，m，n)|=mn+m+n，|V(K1，m，n)|=m+n+1.设V(K1，m，n)={v1，v2，…，vm，w，u1，u2，…，un}.定义图K1，m，n顶点的标号θ如下：

θ(vi)=mn+m+n+1-i，i=1，2，…，m；θ(w)=mn+n；θ(ui)=(m+1)(i-1)，i=1，2，…，n.

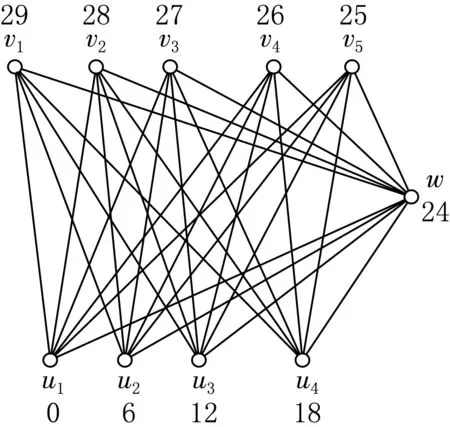
图1 图K1,5,4的优美标号

例如，图K1，5，4的优美标号如图1所示.

令S1={θ(vi)|i=1，2，…，m}∪{mn+n}，S2={θ(ui)|i=1，2，…，n}，则S1∪S2={0，m+1，2(m+1)，…，(n-1)(m+1)，mn+n，mn+n+1，…，mn+n+m}，S1∩S2=∅.因此映射θ：V(K1，m，n)→{0，1，2，…，mn+m+n}是单射.

显然θ(v1)-θ(u1)，θ(v2)-θ(u1)，…，θ(vm)-θ(u1)，θ(w)-θ(u1)，θ(v1)-θ(u2)，θ(v2)-θ(u2)，…，θ(vm)-θ(u2)，θ(w)-θ(u2)，…，θ(v1)-θ(un)，θ(v2)-θ(un)，…，θ(vm)-θ(un)，θ(w)-θ(un)，θ(v1)-θ(w)，θ(v2)-θ(w)，…，θ(vm)-θ(w)是首项为mn+m+n，尾项是1，公差是-1的等差数列，所以θ′：E(K1，m，n)→{1，2，…，mn+m+n}是双射，故θ是图K1，m，n的一个优美标号，图K1，m，n是优美图.

定理2 ∀m∈Z+，图K1，m，2的冠I(K1，m，2)是优美图.

证明根据定理1知图K1，m，2是优美图.下面证明K1，m，2的冠I(K1，m，2)是优美图.由I(K1，m，2)的定义，|V(I(K1，m，2))|=2m+6，|E(I(K1，m，2))|=4m+5.

设V(I(K1，m，n))={v1，v2，…，vm，x1，x2，…，xm，w，z，u1，u2，y1，y2}.定义图I(K1，m，n)顶点的标号θ如下：θ(vi)=4m+6-i，i=1，2，…，m；θ(xm+1-i)=3+2(i-1)，i=1，2，…，m；θ(w)=3m+5；θ(z)=1；θ(u1)=0；θ(u2)=2m+4；θ(y1)=2m+3；θ(y2)=2.

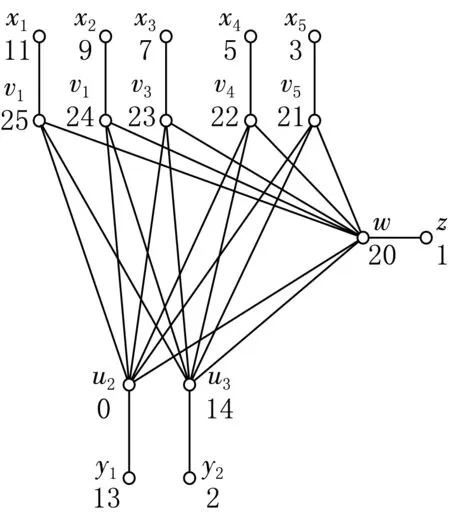
图2 图I(K1,5,2)的优美标号

例如，图I(K1，5，2)的优美标号如图2所示.

令S1={θ(vi)|i=1，2，…，m}∪{θ(w)}，S2={θ(xi)|i=1，2，…，m}∪{θ(z)，θ(y1)}，S3={θ(u1)，θ(u2)，θ(y2)}，则Si∩Sj=∅(1≤i

因为θ(v1)-θ(u1)，θ(v2)-θ(u1)，…，θ(vm)-θ(u1)，θ(w)-θ(u1)，θ(w)-θ(z)，θ(vm)-θ(xm)，θ(vm-1)-θ(xm-1)，…，θ(v1)-θ(x1)，θ(y1)-θ(u1)，θ(y2)-θ(u2)，θ(v1)-θ(u2)，θ(v2)-θ(u2)，…，θ(vm)-θ(u2)，θ(w)-θ(u2)，θ(v1)-θ(w)，θ(v2)-θ(w)，…，θ(vm)-θ(w)是首项为4m+5，尾项是1，公差是-1的等差数列，故θ′：E(I(1-Fm，4))→{1，2，…，4m+5}是双射，从而θ是图I(K1，m，2)的一个优美标号，图I(K1，m，2)是优美图.

定理3 ∀m，n∈Z+，m个顶点的空图记为Em，长为n的路记为Pn，则联图Em∨Pn是优美图.

图3 图Em∨Pn

证明易知|V(Em∨Pn)|=m+n+1，|E(Em∨Pn)|=mn+m+n.设V(Em∨Pn)={u1，u2，…，v1，v2，…，vn+1}，如图3所示.

下文中[x]表示不超过x的最大整数.定义图Em∨Pn顶点的标号θ如下：

θ(ui)=2n+1+(n+1)(i-1)，i=1，2，…，m；

令S1={θ(ui)|i=1，2，…，m}={2n+1，3n+2，4n+3，…，mn+m+n}，S2={θ(vi)|i=1，2，…，n+1}={0，1，2，…，n}，则S1∩S2=∅.因此映射θ：V(Em∨Pn)→{0，1，2，…，mn+m+n}是单射.

注意到{θ(ui)-θ(vj)|i=1，2，…，m；j=1，2，…，n+n}∪{|θ(vj+1)-θ(vj)||j=1，2，…，n}={1，2，…，mn+m+n}，故θ′：E(Em∨Pn)→{1，2，…，mn+m+n}是双射，从而θ是图Em∨Pn的一个优美标号，图Em∨Pn是优美图.

定理4 ∀n∈Z+，图E2∨P2n的冠I(E2∨P2n)是优美图.

证明根据定理3知图E2∨P2n是优美图.下面证明E2∨P2n的冠I(E2∨P2n)是优美图.由I(E2∨P2n)的定义知|V(I(E2∨P2n))|=4n+6，|E(I(E2∨P2n))|=8n+5.设V(I(E2∨P2n))={v1，v2，…，v2n+1，x1，x2，…，x2n+1，u1，u2，y1，y2}.定义图I(E2∨P2n)顶点的标号θ如下：

θ(u1)=8n+5；θ(u2)=6n+4.

θ(x1)=4n+2；θ(x2)=2n+2.

令S1={θ(vi)|i=1，2，…，2n+1}，S2={θ(yi)|i=1，2，…，2n+1}，S3={θ(u1)，θ(u2)，θ(x1)，θ(x2)}，则S1={0，1，2，…，2n}，S2={2n+1，2n+3，2n+5，…，6n+1}，S3={8n+5，6n+4，4n+2，2n+2}，故Si∩Sj=∅(1≤i

因为{θ(ui)-θ(vj)|i=1，2；j=1，2，…，2n+1}∪{θ(u1)-θ(x1)，θ(u2)-θ(x2)}∪{θ(vi)-θ(yi)|i=1，2，…，2n+1}∪{|θ(vi+1)-θ(vi)||i=1，2，…，2n}={1，2，…，8n+5}，故θ′：E(I(E2∨P2n))→{1，2，…，8n+5}是双射，从而θ是图I(E2∨P2n)的一个优美标号，图I(E2∨P2n)是优美图.

[1] 马克杰.优美图[M].北京：北京大学出版社，1991：128-158.

[2] GALLIAN J A.A dynamic survey of graph labeling [J].The Electronic Journal of Combinatorics，2016，DS6：1-306.

[3] ALON N.Combinatorics，probability and computing [M].Cambridge：Cambridge University Press，1999：150-236.

[4] ZHOU XIANG-QIAN，YAO BING，CHEN XIANG-EN，et al.A proof to the odd-gracefulness of all lobsters [J].Ars Combinatorial，2012，103：13-18.

[5] KATHIESAN K M.Two classes of graceful graphs[J].Ars Combinatorial，2000，22：491-504.

[7] 唐保祥，任韩.2优美图的冠的优美标号[J].中山大学大学报(自然科学版)，2015，54(5)：24-27.

[8] 容青，熊冬春.P2r，b图的优美性[J].系统科学与数学，2010，30(5)：703-709.

[9] 唐保祥，任韩.2类优美图[J].山东大学学报(理学版)，2010，45(10)：45-48.

[10] 唐保祥，任韩.3类特殊图的优美性[J].武汉大学学报(理学版)，2014，60(6)：553-556.

[11] 张志尚，黄文强.两类并图的优美标号[J].东北师大学报(自然科学版)，2013，45(2)：30-34.

(责任编辑：李亚军)

Thegracefullabelingoftwokindsgraphsanditscoronas

TANG Bao-xiang1，REN Han2

(1.School of Mathematics and Statistics，Tianshui Normal University，Tianshui 741001，China； 2.Department of Mathematics，East China Normal University，Shanghai 200062，China)

Constructive method for gracefulness of two kinds graphs and corona for two kinds of graphs was studied.The conclusions were obtained as：for arbitrary positive integern，m，Embe a empty graph withmvertices，Pnbe a path withn+1 vertices，the complete 3-partite graphsK1，m，n，I(K1，m，2)，a join graphEm∨PnandI(E2∨P2n) are graceful graphs.

path；join of two graphs；empty graph；corona；graceful graph

1000-1832(2017)03-0158-03

10.16163/j.cnki.22-1123/n.2017.03.031

2016-01-27

国家自然科学基金资助项目(11171114).

唐保祥(1961—)，男，教授，主要从事图论和组合数学研究.

O 157.5 [学科代码] 110·7470

A