两类特殊Corona图的b-染色数与b-连续性

代天骄，姚 兵

(1.山东大学数学学院，山东 济南 250100； 2.西北师范大学数学与统计学院，甘肃 兰州，730070)

两类特殊Corona图的b-染色数与b-连续性

代天骄1，姚 兵2

(1.山东大学数学学院，山东 济南 250100； 2.西北师范大学数学与统计学院，甘肃 兰州，730070)

构造了两个特殊模型：路图(圈)与完全图中去掉一个匹配所构成图的Corona图.研究了这两个特殊Corona图的m-度与b-染色数，并证明了它们是b-连续的.

m-度；b-染色；b-染色数；b-连续；Corona图；完全图；完美匹配

1999年，Irving等[1]在图的a-染色基础上提出了图的b-染色：在一个图G的正常k染色中，如果每一个颜色类中都至少存在一个顶点，使得在其他的k-1个颜色类中都至少存在一个邻点，则称这样的正常k染色为b-染色.一个图G的b-染色数为最大的正整数k，如果用k种颜色能够对G进行b-染色，并记为b(G).同时其给出了b-染色数的一个上界m(G)，即图G的m-度，并证明了确定一个一般图G的b-染色数b(G)是一个NP-完全问题，同时求得了树图的b-染色数.从此，有关b-染色的问题便引起了众多学者的关注.

Effantin和Kheddouci[2-4]研究了路、圈以及完全二元树图和完全毛毛虫图的b-染色数.2004年，Faik[5]又证明了弦图是b-连续的.2012年，Vernold等[6]证明了对于任意含有n个顶点的两个图G1与G2，Corona图G=G1∘G2是可b-染色的，且研究并证明了G1与G2在不同情形下的Corona图G=G1∘G2的b-染色数.该文还提出了对于任意具有n个顶点的两个图G1与G2的Corona图G=G1∘G2，或特殊的Corona图G=G1∘G2可能是b-连续和b-单调的.

在文献[6]的启发下，本文研究了两类特殊的模型：路图或圈图与在完全图中去掉一个匹配所构成图的Corona图.研究了这两类特殊Corona图的m-度与b-染色数，并证明了它们是b-连续的.

1 预备知识

本文涉及的图均为简单、无向的有限图.

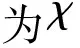
定义1.2[1]在一个图G的正常k染色中，如果每一个颜色类中都至少存在一个顶点，使得在其他的k1个颜色类中都至少存在一个邻点，则称这样的正常k染色为b-染色，这样的顶点称为b-染色顶点.一个图G的b-染色数为最大的正整数k，使得用k种颜色能够对G进行b-染色，并用b(G)表示.

n阶完全图是指n阶的简单图，且任意两个不同的顶点都有边相连.设图G=(V，E)的顶点v1，v2，…，vn按照顶点的度降序排列，即d(v1)≥d(v2)≥…≥d(vn)，图G的m-度定义为

m(G)=max{i|d(vi)≥i-1，1≤i≤n}.[1]

图G的边子集M称为图G的一个匹配，如果M中的任意两条边互不相邻.若G的每个顶点是M中一条边的端点，则称匹配M饱和G的每个顶点，称匹配M是图G的一个完美匹配.

对于图G1与G2，称图G=G1∘G2为图G1与G2的Corona图，如果G包含G1的一个拷贝，包含了G2的|V(G1)|个拷贝，且G1的第i个顶点与G2的第i个拷贝的所有顶点都邻接.[6]

引理1.1[1]设G是任意图，则b(G)≤m(G).

2 主要结论及证明

引理2.1 设n为任意正整数，Pn为含有n个顶点的路图，K2n为含有2n个顶点的完全图，M为K2n的一个完美匹配.则

m[Pn∘(K2n-M)]=2n.

证明设路Pn的顶点集为V(Pn)={v1，v2，…，vn}，其中

d(v1)=d(vn)=1，d(v2)=d(v3)=…=d(vn-1)=2.

设K2n-M的顶点集为

V(K2n-M)={u1，u2，…，u2n}，

从而Corona图Pn∘(K2n-M)的顶点集可表示为

V(Pn∘(K2n-M))={vi|1≤i≤n}∪{uij|1≤i≤n，1≤j≤2n}.

由Corona图的定义可知，对于任意的顶点vi∈V(Pn∘(K2n-M))，vi与集合{uij|1≤j≤2n}中的任意顶点都是邻接的.在图Pn∘(K2n-M)中，有n个度不小于2n+1的顶点，有2n2个度为2n-1的顶点，即

d(v1)=d(vn)=2n+1，d(v2)=d(v3)=…=d(vn-1)=2n+2，d(uij)=2n-1.

故由图的m-度定义可知

m[Pn∘(K2n-M)]=2n.

定理2.1 设n为任意正整数，Pn为含有n个顶点的路图，K2n为含有2n个顶点的完全图，M为K2n的一个完美匹配.则有

b[Pn∘(K2n-M)]=m[Pn∘(K2n-M)]=2n，

且Pn∘(K2n-M)是b-连续的.

证明设路Pn的顶点集为

V(Pn)={v1，v2，…，vn}，

其中

d(v1)=d(vn)=1，d(v2)=d(v3)=…=d(vn-1)=2.

设K2n-M的顶点集为

V(K2n-M)={u1，u2，…，u2n}，

从而Corona图Pn∘(K2n-M)的顶点集可表示为

V(Pn∘(K2n-M))={vi|1≤i≤n}∪{uij|1≤i≤n，1≤j≤m}.

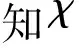
(1) 对Corona图G=Pn∘(K2n-M)中的n个顶点v1，v2，…，vn用颜色1，2，…，n进行染色.

(2) 对于与任意顶点vi(1≤i≤n)相邻的2n个顶点ui1，ui2，…，ui2n进行染色.将图K2n-M中的2n个顶点按照顶点的对称性分成两部分：A={ui1，ui2，…，ui(n-1)，uin}与B={ui(2n)，ui(2n-1)，…，ui(n+1)}.其次，对于A中的n个顶点，对ui2用第n+i色进行染色，其他n-1个顶点用[1，n]{i}里的颜色依次进行染色；对于B中的n个顶点，在M中与ui2相邻的顶点ui(2+n+1)用第n+i色进行染色，其他n-1个顶点中，有a-1个顶点分别用第{n+1，n+2，…，n+a}{n+i}颜色进行染色，余下的n-a个顶点分别按照在原K2n中构成完美匹配且被去掉的那个匹配所对应的端点染相同颜色.采用通用b-染色方案，用k种颜色就可以对Corona图G=Pn∘(K2n-M)实现b-染色，结论得证.

综上所述，对于任意的正整数n，Corona图Pn∘(K2n-M)是b-连续的，有

b[Pn∘(K2n-M)]=m[Pn∘(K2n-M)]=2n.

引理2.2 设Cn为含有n个顶点的圈图，K2n为含有2n个顶点的完全图，M为K2n的一个完美匹配.则

m[Cn∘(K2n-M)]=2n.

证明设圈Cn的顶点集为

V(Cn)={v1，v2，…，vn}，

其中

d(v1)=d(v2)=…=d(vn-1)=d(vn)=2.

设K2n-M的顶点集为

V(K2n-M)={u1，u2，…，u2n}，

从而Corona图Cn∘(K2n-M)的顶点集可表示为

V(Cn∘(K2n-M))={vi|1≤i≤n}∪{uij|1≤i≤n，1≤j≤m}.

由Corona图的定义，对于任意顶点vi∈V(Cn∘(K2n-M))，vi与集合{uij|1≤j≤m}中的任意顶点都是相邻的.在图Cn∘(K2n-M)中，有n个度为2n+2的顶点，有2n个度为2n-1的顶点，即

d(v1)=d(v2)=…=d(vn)=2n+2，d(uij)=2n-1，

从而由m-度的定义得m[Cn∘(K2n-M)]=2n.

定理2.2 设n为任意正整数，Cn为含有n个顶点的圈图，K2n为含有2n个顶点的完全图，M为K2n的一个完美匹配.则

b[Cn∘(K2n-M)]=m[Cn∘(K2n-M)]=2n，

且Cn∘(K2n-M)是b-连续的.

证明设圈Cn的顶点集为

V(Cn)={v1，v2，…，vn}，

其中

d(v1)=d(v2)=…=d(vn-1)=d(vn)=2.

设K2n-M的顶点集为

V(K2n-M)={u1，u2，…，u2n}，

从而Corona图Cn∘(K2n-M)的顶点集可表示为

V(Cn∘(K2n-M))={vi|1≤i≤n}∪{uij|1≤i≤n，1≤j≤m}.

(1) 对Corona图G=Cn∘(K2n-M)中的n个顶点v1，v2，…，vn用颜色1，2，…，n进行染色.

(2) 对于与任意顶点vi(1≤i≤n)相邻的2n个顶点ui1，ui2，…，ui2n进行染色.将图K2n-M中的2n个顶点按照顶点的对称性分成两部分：A={ui1，ui2，…，ui(n-1)，uin}与B={ui(2n)，ui(2n-1)，…，ui(n+1)}.前一部分A中的n个顶点用第n+i色对每个ui2进行染色，其他n-1个顶点用[1，n]{i}里的颜色依次进行染色.对于B中的n个顶点，在M中与ui2相邻的顶点ui(2+n+1)用第n+i色进行染色；其他n-1个顶点中，有a-1个顶点分别用第{n+1，n+2，…，n+a}{n+i}颜色进行染色，余下的n-a个顶点分别按照在原K2n中构成完美匹配且被去掉的匹配所对应的端点染相同颜色.采用通用b-染色方案，用k种颜色就可以对Corona图G=Cn∘(K2n-M)实现b-染色.

综上所述，对于任意的正整数n，Corona图Cn∘(K2n-M)是b-连续的，且

b[Cn∘(K2n-M)]=m[Cn∘(K2n-M)]=2n.

3 结束语

在Vernold等工作的启发下，构造了两类特殊的模型：路图(圈)与完全图中去掉一个匹配所构成图的Corona图，研究了这两类特殊Corona图的m-度与b-染色数，并证明其皆是b-连续的.接下来，将重点研究对于更为一般的两个图G1与G2所构成的Corona图G1∘G2的b-染色数与b-连续性，以期得到较为深刻和广泛的结果.

[1] IRVING R W，MANLOVE D F.Theb-chromatic number of a graph[J].Discrete Applied Mathematics，1999，91(1/2/3)：127-141.

[2] EFFANTIN B.Theb-chromatic number of power graphs of complete caterpillars[J].Discrete Math Science & Cryptograph，2005，8(3)：483-502.

[3] EFFANTIN B，KHEDDOUCI H.Theb-chromatic number of some power graphs[J].Discrete Math Theor Comput Sci，2003，6(1)：45-64.

[4] EFFANTIN B，KHEDDOUCI H.Exact values for theb-chromatic number of a power completek-arytree[J].Discrete Math Sci Cryptogr，2005，8：117-129.

[5] FAIK T.About theb-continuity of graphs[J].Electronic Notes in Discrete Mathematics，2004，17：151-156.

[6] VERNOLD V J，VENKATACHALAM M.Theb-chromatic number of Corona graphs[J].Utilitas Mathematica，2012，88：299-307.

[7] 迪斯特尔 R.图论[M].于青林，王涛，王光辉，等译.第4版.北京：高等教育出版社，2013：108-109.

(责任编辑：李亚军)

Theb-chromaticnumberandb-continuityofthetwotypesofspecialCoronagraphs

DAI Tian-jiao1，YAO Bing2

(1.School of Mathematics，Shandong University，Jinan 250100，China； 2.College of Mathematics and Statistics，Northwest Normal University，Lanzhou 730070，China)

The two types of special Corona graphs are researched.Them-degree andb-chromatic number of these graphs are studied.Theb-continuity of these graphs is given.

m-degree；b-coloring；b-chromatic number；b-continuous；Corona graph；complete graph；perfect matching

1000-1832(2017)03-0034-04

10.16163/j.cnki.22-1123/n.2017.03.008

2015-12-31

国家自然科学基金资助项目( 61163054，61363060，61662066).

代天骄(1995—)，女，硕士，主要从事图着色与标号以及复杂网络研究；通信作者：姚兵(1956—)，男，教授，主要从事图着色与标号以及复杂网络研究.

O 211.2 [学科代码] 110·7470

A