一类轴承转子系统的全局动力学行为分析

刘熙娟，刘 云，褚衍东，郭丽峰

(1.塔里木大学信息工程学院，新疆 阿拉尔 843300； 2.兰州交通大学数理学院，甘肃 兰州 730070)

一类轴承转子系统的全局动力学行为分析

刘熙娟1，刘 云1，褚衍东2，郭丽峰1

(1.塔里木大学信息工程学院，新疆 阿拉尔 843300； 2.兰州交通大学数理学院，甘肃 兰州 730070)

研究了一类电磁轴承转子系统在1∶2内共振情形下的全局动力学行为.用数值仿真验证了理论的正确性.其分析结果对抑制转子系统的内共振运动有重要意义.

多尺度法；同宿轨道；电磁轴承转子系统；范式理论

电磁轴承转子属于轴承转子中的一类，和传统转子相比具有低摩擦、低功耗、非接触等优点，因此在各个领域被广泛应用.但随着人们的使用，发现该类轴承转子的运动是很不稳定的，时常有混沌现象发生，这直接影响磁悬浮轴承转子系统的使用性能.对轴承转子系统的动力学行为的研究，前人已做了大量工作.[1-5]本文从理论上分析了一类二自由度电磁轴承转子系统的混沌特性，并采用数值模拟来验证理论分析的正确性.

1 数学模型

电磁轴承转子系统的运动方程[6]可表示为

(1)

(2)

(3)

(4)

(5)

2 多尺度法获得规范型

利用Taylor展开式，可得(3)与(4)式在原点处的泰勒多项式，省去高阶项，有

(6)

同理，对(5)式在原点处进行Taylor展开，并保留三阶项，可得其Taylor多项式

其中

(7)

其中

为了对电磁轴承转子系统进行控制，可改变系统的刚度.比如令控制器的比例系数为k1=k0+kcosΩt，得到变刚度的转子动力学方程.将变刚度的电磁轴承转子系统的无量纲方程改写为

为便于多尺度法的研究，引进小参数ε，则原系统方程可表示为

(8)

本文只考虑系统发生1∶2内共振的情形，ε为小扰动参数，共振关系为

其中σ1，σ2为调谐参数，为了方便研究取Ω=2.

(9)

ε1：

(10)

方程(9)的通解为

(11)

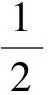
(12)

令

A1(T1)=x1(T1)+iy1(T1)，A2(T1)=x2(T1)+iy2(T1).

(13)

把(13)式代入(12)式，分离所得结果的实部和虚部可得直角坐标形式下的平均方程

(14)

在没有扰动参数ε的情况下，系统(14)有零解(x1，y1，x2，y2)=(0，0，0，0)，此零解的雅可比矩阵为

从十年前后所呈现学习材料的对比中清晰地看出，十年前的教学材料绝大部分是教师“给的”，而十年后所用学习材料基本来自学生，尤其是新知探究学习过程中几乎所有的学习素材都由学生创作提供，教师选择学习材料的范围大大增加，也给教师调控的能力带来了极大的挑战！教师要快速参与学生间的学习，选择合适的学习材料促进学生对“倍”内涵的理解。而学生可根据自己的学习能力获得不同的学习体会和收获，有了更大的学习时空和创新机会，充分体现了学生的主体地位。

(15)

系统(15)的雅可比矩阵为

系统(15)是四阶三维系统，由文献[10]中Maple程序可得其规范型.系统(14)带参数的规范型为

(16)

为了获得全局分岔所需的标准型，引入线性变换

(17)

(18)

其中

(19)

此处的Hamilton函数H为

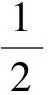
(20)

3 未扰动系统的全局分岔分析

令ε=0，得到系统(18)的未扰动方程

(21)

显然系统的前三个方程与φ无关，I为常数，从而(u，v)平面的动力学行为与(I，φ)平面的行为是互相解耦的.(u，v)相空间中的所有平衡点可描述为

(22)

(23)

是一个二维不变流形，且由文献 [11] 可知其为一个正规双曲的二维不变流形，该二维正规双曲不变流形包括三维稳定和不稳定流形，分别用Ws(M0)，Wu(M0)表示.

为分析系统(21)的异宿分岔，得到未扰动系统的异宿轨线的分析表达式

(24)

此外，常规双曲流形M0由下面的方程决定：

(25)

(26)

4 扰动系统的全局分岔分析

本节将用到两种不同的坐标集合(u，v，I，φ)和(u，v，h，φ).由(23)式知M0是正规双曲不变流形，在充分可微的小扰动下，M与它的稳定流形和不稳定流形是不变的，因此M0→Mε.从而限制在Mε上的系统(18)的扰动方程可以描述为

(27)

将以上变换代入(27)式可得

(28)

令ε→0，系统(28)变为

(29)

未扰动系统(29)是带有Hamilton函数的Hamilton系统，其Hamilton函数为

系统(29)的不动点为

(30)

对上述不动点对应的雅可比矩阵进行分析可知，p是鞍点，q是中心.于是存在一个同宿轨道连接p和它本身.根据Kovacic[11]的分析，对于充分小的参数ε，q会成为汇qε，p依然是鞍点pε.此时中心点q的周围不存在周期轨道，连接p和p自身的同宿轨道也随之消失，并有不稳定流形慢慢靠近qε.

(31)

由文献[12] 可知对一个扰动系统来说，鞍焦点qε有一条同宿轨道，该同宿轨道从环形区域出发，又返回到该环形域，最后产生了Silnikov型同宿环.

为证明Silnikov型同宿轨道的存在，需分两步验证.[11]首先通过高维Melnikov理论找到Wu(qε)⊂Ws(qε)的条件，即离开qε的轨线是否会回到Aε的邻域内.其次确定轨道是否回到Aε的吸引域里.Silnikov理论可以探测到Wu(qε)和Ws(qε)之间的距离，根据上述分析以及参考文献中的结论，得到高维系统的Silnikov函数

(32)

其中函数H，gv，gI的表达式由(19)和(20)式给出.

对(32)式的前三项进一步简化，最后可得Melnikov函数的表达式

(33)

为确定Silnikov型同宿轨道的存在性，首先要求Melnikov函数有一个简单零点，即

(34)

若Wu(qε)能够回到qε的吸引域，则需满足

φs<φc+Δφ+mπ<φn，

(35)

其中m是整数，φs，φc，φn分别由方程(30)和(31)给出.

若(34)式存在简单零点，则(35)式也成立.这表明系统(18)存在Silnikov型同宿轨道，即系统(18)可以产生Smale马蹄意义下的混沌现象，这说明在整个四维系统中存在混沌运动.

5 数值仿真

选取系统的参数为W=0.0，a=0.24，P=1.1，D=0.03，μ=0.3，U=0.2，K=2.0，对方程(2)进行数值模拟，对应的相图见图1.

(1)x-dx相图 (2)x-dy相图

接下来对系统的平均方程(14)进行数值仿真，为了方便研究，这里忽略掉参数的机械意义.取系统的初值为(0.1，0.8，0.15，0.01)，其对应的相图如图2所示.

(1)x1-y1相图 (2)x1-y2相图

平均方程(14)和原系统方程(2)的数值仿真结果表明：在一定条件下，平均方程中的混沌运动导致了原系统方程中的调幅混沌运动.从理论分析和数值模拟都可以看出，利用平均方程可以定性、定量地分析原系统的混沌动力学行为.

[1] KIRK R G.Evaluation of AMB turbo machinery auxiliary bearings[J].ASME J Vib Acoust，1999，121：156-161.

[2] COLE M O T，KEOGH P S.The dynamic behavior of a rolling element auxiliary bearing following rotor impact[J].ASME J Tribol，2002，124：406-413.

[3] 孙保苍，梁荣生，陈威.磁悬浮轴承-转子系统非线性行为的控制[J].噪声与振动控制，2011(3)：11-15.

[4] 朱熀秋，徐龙祥.径向四自由度磁悬浮轴承控制器研究与探讨[J].应用科学学报，2002(3)：20-26.

[5] 韩清凯，于涛，王德友，等.故障转子系统的非线性振动分析与诊断方法[M].北京：科学出版社，2010：89-103.

[6] INAYAT-HUSSAIN J I.Nonlinear dynamics of a magnetically supported rigid rotor in auxiliary bearings[J].Mechanism and Machine Theory，2010，45：1651-1667.

[7] CHAVEZ J P，WIERCIGROCH M.Bifurcation analysis of periodic orbits of a non-smooth Jeffcott rotor model[J].Communications in Nonlinear Science and Numerical Simulation，2013，18：2571-2580.

[8] THOTA P，DANKOWICZ H，TC-HAT.A novel toolbox for the continuation of periodic trajectories in hybrid dynamical systems[J].SIAM Journal of Applied Dynamical Systems，2008(7)：1283-1322.

[9] 刘习君，贾启芬.工程振动理论与测试技术[M].北京：高等教育出版社，2004：292-307.

[10] ZHANG W.Global and chaotic dynamics for a parametrically excited thin plate[J].Journal of Sound and Vibration，2001，239(5)：1013-1036.

[11] KOVACIC G，WIGGINS S.Orbits homoclinic to reasonance with an application to chaos in a model of the forced and damped sine-Gordon equation[J].Physica，1992，57：182-225.

[12] FENG Z C，WIGGINS S.On the existence of chaos in a parametrically forced mechanical systems with broken O(2)symemetry[J].Zeitschriftfuer Angewandte Mathematic and Physicalische，1993，44：201-248.

[13] 杜文举，俞见宁，张建刚，等.一个新四维混沌系统的分岔分析[J].东北师大学报(自然科学版)，2014，46(1)：80-88.

(责任编辑：李亚军)

Globaldynamicsofaclassofbearing-rotorsystem

LIU Xi-juan1，LIU Yun1，CHU Yan-dong2，GUO Li-feng1

(1.College of Information Engineering，Tarim University，Aral 843300，China； 2.School of Mathmatics and Physics，Lanzhou Jiaotong University，Lanzhou 730070，China)

The internal resonance is studied by adopting the method of multiple scales and the normal form theory，and the global bifurcation dynamics of the system are obtained.This precedes a new theoretical basis in protecting the rotor from the resonant failures in the turbine machinery.

the multiple scales；homoclinic orbit；magnetic bearing rotor system；normal form theory

1000-1832(2017)03-0022-07

10.16163/j.cnki.22-1123/n.2017.03.006

2015-11-03

国家自然科学基金资助项目(11161027).

刘熙娟(1988—)，女，讲师，主要从事非线性动力学研究；通信作者：郭丽峰(1983—)，男，讲师，主要从事混沌控制和应用研究.

O 193 [学科代码] 110·5110

A