建筑微型热电联供方案的区间数TOPSIS排序

阮红权,高欣,谭丽君

(1.同济大学经济与管理学院,上海200092;2.新奥能源服务(上海)有限公司,上海200082; 3.上海大学理学院,上海200444)

建筑微型热电联供方案的区间数TOPSIS排序

阮红权1,2,高欣1,谭丽君3

(1.同济大学经济与管理学院,上海200092;2.新奥能源服务(上海)有限公司,上海200082; 3.上海大学理学院,上海200444)

微型热电联供(micro-combined heat and power,micro-CHP)有利于提高能效和保护环境,是建筑供能发展的方向之一.规划阶段micro-CHP方案评价是项目成功的关键步骤.为了使方案的区间数指标可以应用于逼近理想解的排序(technique for order preference by similarity to an ideal solution,TOPSIS),首先用理想解区间计算距离范围、相对接近程度;然后定义可接受函数对方案进行排序.通过适用于小型建筑的4种方案为例验证了该方法的可行性和适用性.

微型热电联供;多属性决策;区间数;逼近理想解的排序

根据国际能源署发布的《世界能源展望2014》(World Energy Outlook 2014),2012年建筑部门能源消费占全球终端能耗的32.8%.中国2013年建筑总能耗(不含生物质能)为7.56亿吨标准煤当量(ton of standard coal equivalent,TCE),占全年能源消费总量的19.5%,且建筑能耗总量还将进一步大幅增长[1].能源危机和环境危机的双重作用促使学者们反思建筑供能发展的历史道路,进而寻求一条人与自然和谐共存的新途径.热电联产(combined heat and power,CHP)被广泛认为是一种能够部分解决和缓解能源相关问题的有效方式.随着科技的全面进步,在热电联产基础上发展起来的微型热电联供(micro-CHP)正成为研究的新方向,有望成为建筑领域提高能效、节约能源的发展方向.谢德平等[2]对几种主要micro-CHP进行了比较.Barbieri等[3]对家庭或小型商业的micro-CHP进行了分析,证明了其能一定程度地提升能源利用效率并减少对环境的影响.从已有的研究中发现,探索适合建筑的micro-CHP大多只从技术、经济或环保的单一角度出发,而从可持续发展的角度综合考虑技术、经济、环境和社会属性的研究尚不多见.

逼近理想解的排序(technique for order preference by similarity to an ideal solution, TOPSIS)是多属性决策问题的一种重要方法,可根据不同方案到正负理想解的距离对方案优劣进行评价.由于简单实用,TOPSIS在多属性决策中的应用较为广泛.但在项目的规划阶段对micro-CHP方案进行多属性评价时,由于资料、时间等条件限制,研究比较粗略,决策者往往会采用区间数评价定量指标(这里的评价指标即是指决策中的属性),以及语言信息评价定性指标,因而无法直接应用TOPSIS进行决策.针对如何将具有模糊性的区间数应用于TOPSIS,已经引起了有关学者的重视.Jahanshah loo等[4-5]对TOPSIS进行了拓展并将其应用到求解属性值为区间数的多属性决策问题.Sayadi等[6]、Yue[7]在VIKOR方法的研究中采用了类似的方法.随后张英俊等[8]、Dymova等[9]、Liu等[10]又相继提出了改进的TOPSIS法.这些方法都是将区间数确定化,即用实数值理想解表示方案与理想解的接近程度,但这会造成区间信息不同程度的丢失.鉴于此,本工作在已有研究的基础上提出用理想解区间计算每个方案到其相应理想解的距离范围、相对接近程度,然后再定义可接受函数对4个micro-CHP方案进行排序.

1 建筑微型热电联供方案及其属性

Micro-CHP是在CHP的基础上发展而来的.CHP在整个能量生产、供应的系统范围内既供应电能又供应热能,而且其供热是全部或部分利用热变功过程中的低品位热能,综合能源利用效率可以达到75%左右.以供热工况为例,假设用户需要30 kW·h的电、45 kW·h的热,而燃煤CHP由于利用了低温抽汽的热能,耗煤量仅需100 kW·h左右,若燃煤热电分产,因为大量能量通过冷凝潜热排弃到环境中,耗煤量近154 kW·h(见图1).CHP在能源利用效率方面取得的进步不仅是建筑业的一个全新选择,对于城市现有的各种能源供应体系,以及城市规划都将是一次划时代的革命.CHP着眼于一次能源转换效率,但在建筑用能中只比热电分产多解决了制冷季的供暖,加之碳减排的压力,进一步压缩了燃煤CHP的发展空间[11].

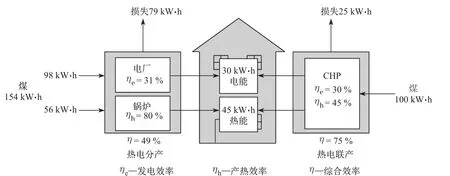
图1 燃煤热电联产与热电分产的能源利用效率比较Fig.1 Energy effi ciency comparisons between coal-fi red CHP and separate generation of heating and power

科技进步催生了各种以非煤能源为燃料的、靠近用户的小容量CHP,它们都属于分布式能源范畴.一般定义电输出功率100～200 kW的系统为小规模热电联供(small scale CHP), 10～100 kW的为小型热电联供(mini-CHP),小于10 kW的为micro-CHP.Micro-CHP整合了相关领域的最新技术,适用于单户住宅、小型商业、小型办公等建筑,是建筑供能发展的方向之一,其优势如下:①micro-CHP布置在建筑内,几乎不需要或只需要很短的输送线路,能量输送成本几乎为0;②在满足新用户、特殊用户的用能需求时,可简单安装,灵活、方便、便宜地为用户提供能量,延缓输、配电网的升级换代;③附加其他设备后可以同时“就地直供”电、冷、暖和卫生用水,实现能源的综合梯级利用,提高能源利用效率;④利用非煤能源作为燃料,提升能源利用效率,减少污染物的排放.

规划阶段micro-CHP方案评价是项目成功的关键步骤.目前,适合于小型建筑的大部分是基于内燃机、微型燃气轮机、斯特林机和燃料电池方案的micro-CHP.内燃机以天然气、生物质气、柴油、燃油等为燃料,将燃料释放的热能转化成机械能,从而驱动压缩机和发电机工作.内燃机发电投资较小、启动迅速、可靠性高、变负荷性能好、余热可以回收,是世界上应用最广的分布式能源技术.微型燃气轮机利用天然气、生物质气、柴油、汽油、醇类等燃料驱动燃气轮机并发电,将排气引入余热锅炉内,以低压蒸汽或热水形式回收,满足用户采暖、空调和热水的要求.微型燃气轮机是一种清洁、可靠、多用途、小型的实现热电冷多联供的能源新技术.斯特林机是一种外燃式的闭式循环热力发动机,它的工质封在气缸里,受热膨胀后推动活塞,使发动机对外输出功率.燃料在气缸外连续燃烧,通过加热器将热量传给工质,工质不参与燃烧.因此,斯特林机具有燃料适应性效率高、排放低与噪声低等特点.燃料电池是一个电化学系统,能将化学能直接转换为电能和热能.一般来说,燃料电池的发电效率比其他发电装置高1/6～1/3,综合热效率可达80%,具有发电效率高、噪声小、小型高效、污染物排量小等优点,但其启动需要一定的时间.

基于以上4种方案micro-CHP的主要评价指标[2,12-13]如表1所示.技术属性(电效率、总效率)是micro-CHP推广的基础;经济属性(投资成本、维护成本)是投资者关心的重点.随着各界对环境保护的日益重视,环境属性(噪声、CO2排放)也受到很大关注.其他一些属性,如使用寿命、燃料适应性、占用空间的大小,标志了micro-CHP对于小型建筑的适用性,属于社会属性层面.

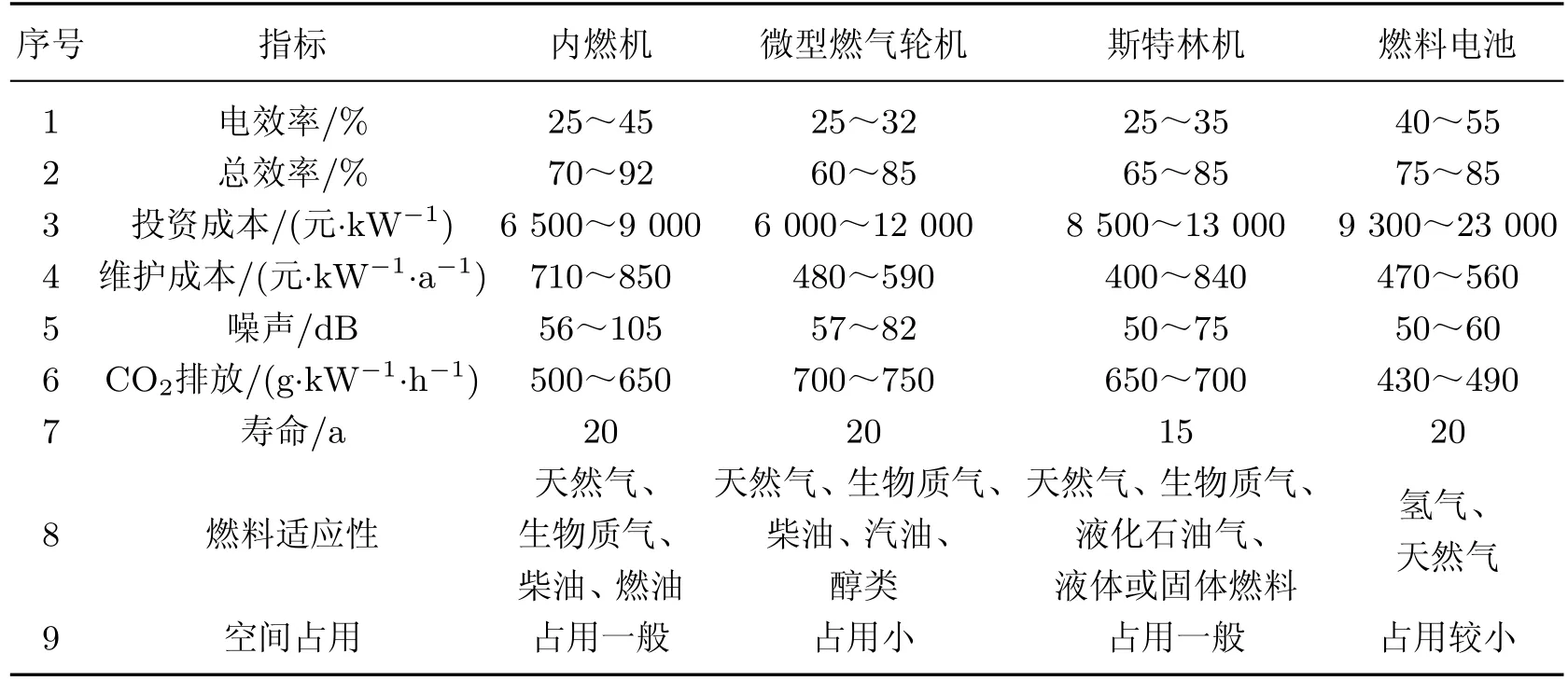
表1 几种micro-CHP方案的评价指标Tab le 1 Criteria for sorting of themicro-CHP schemes

显然,micro-CHP方案的选择与技术、经济、环境、社会等存在复杂的相互作用(见图2).为实现建筑能源的可持续发展,要求决策者能够进行多方面的权衡.

图2 供能系统与外部环境之间的复杂关系Fig.2 Complex interactions of energy supply system

2 区间数TOPSIS法

多属性决策问题可以表述为用i=1,2,···,m个方案对j=1,2,···,n个属性进行评价,选出最优方案.通常将一个多属性决策问题转换为如表2所示的决策矩阵,其中Ai为第i个方案,Cj为第j个属性,Xij为第i个方案的第j个指标的属性值.

表2 多属性决策矩阵Tab le 2 Multi-criteria decision matrix

TOPSIS的基本思想是根据有限个评价对象分别与正理想解和负理想解的接近程度进行排序.所谓理想解是事先假定的某一最优的解,即所有属性值都达到各备选方案中的最优值;而负理想解是所设想的最劣解.因此所需的最优方案就是最接近正理想解,同时又远离负理想解的方案.

由表2可见,决策方案的属性值往往无法使用一个确定的数值来衡量,大多数情况下只能确定一个区间.传统的TOPSIS无法直接用于解决这类问题,需要对其进行方法改进.

定义1若X=[xl,xu]={x|xl≤x≤xu,x∈R},则称X为实数域上的区间数.

根据定义1,将表2的多属性决策矩阵转换为如表3所示的区间数多属性决策矩阵.

表3 区间数多属性决策矩阵Tab le 3 Multi-criteria decision matrix with interval data

2.1 区间数的规范化处理

第i个方案第j个属性区间可以规范化为

若要对不同的属性值赋予其相应的权重ωj(j=1,2,···,n),得到规范化后的属性值为

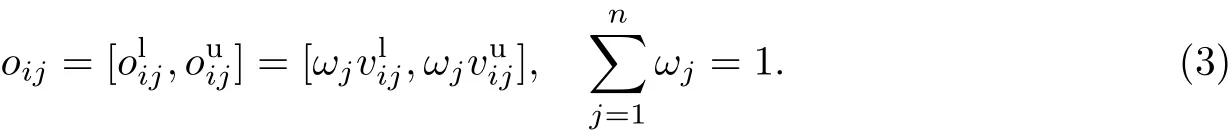
2.2 理想解的确定

在区间数TOPSIS研究方面,文献[4-10]都是最终将区间数转化成确定数进行排序,造成信息丢失.对此,在已有研究基础上,本工作提出以下改进方法,即用正理想解区间和负理想解区间来替代实数值理想解.相对于第k(k=1,2,···,m)个方案Ak而言的理想解,通过以下方法确定.

(1)正理想解的上界.使所有方案处于最有利的情形(即效益型属性值最大,同时成本型属性值最小),由此确定对于方案Ak而言的正理想解的上界:

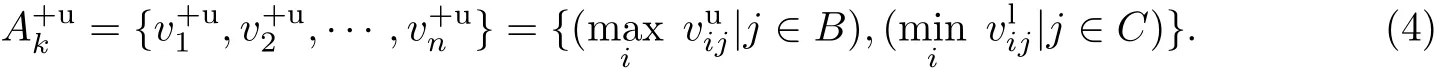
(2)正理想解的下界.使第k个方案处于劣势的情形而其他方案处于最有利的情形,由此确定对于方案Ak而言的正理想解的下界:

(3)负理想解的上界.使第k个方案处于最有利的情形而其他方案处于最劣势的情形,由此确定对于方案Ak而言的负理想解的上界:

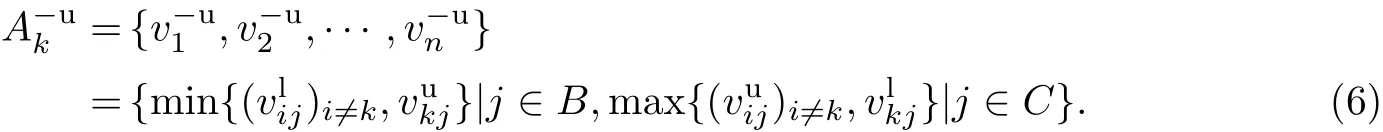
(4)负理想解的下界.使所有方案处于最劣势的情形,由此确定对于方案Ak而言的负理想解的下界:

上述确定理想解的方法可以用图3表示.设有两个备选方案(方案1与方案2)以及两个评价方案的指标(指标1(效益型指标)与指标2(成本型指标)).在图3中,B点就是方案1的正理想解的上界,即(此时方案1与方案2均处于有利情形);C点就是方案1的正理想解的下界,即(此时方案1处于劣势情形,方案2处于有利情形);D点就是方案1的负理想解的下界,即(此时方案1与方案2均处于劣势情形);此处重合.一般情况下,,则方案Ak的理想解也是一个区间数.

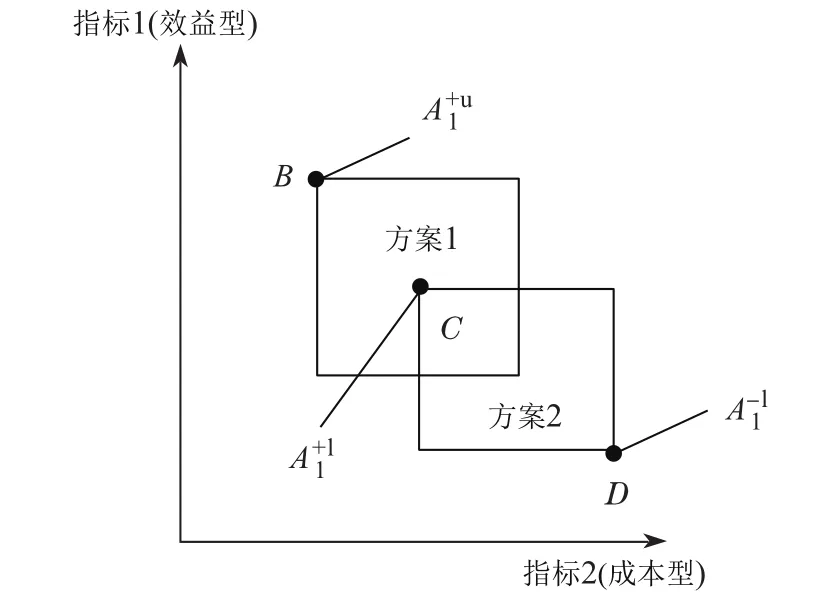
图3 理想解的上界和下界Fig.3 Upper and lower bounds of the ideal solution

2.3 计算每个方案到其相应理想解的距离范围

借鉴传统TOPSIS的欧几里德范数,每个方案到区间数理想解的距离范围也是一个区间数.

(1)使第k个方案处于劣势的情形,其与相应的正理想解的上界的距离为

该值表示第k个方案与其正理想解的距离的上界.

(2)使第k个方案处于有利的情形,其与相应的正理想解的下界的距离为

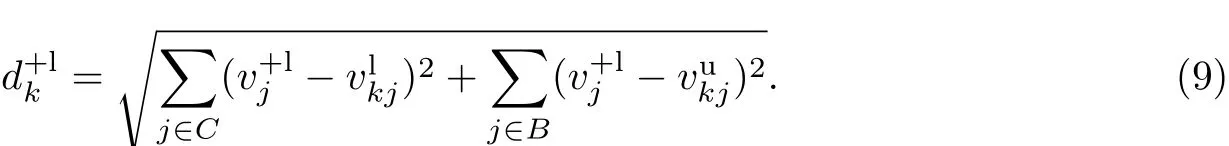
该值表示第k个方案与其正理想解的距离的下界.

(3)使第k个方案处于有利的情形,其与相应的负理想解的上界的距离为

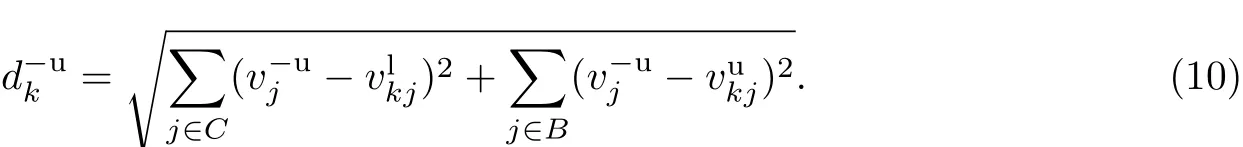
该值表示第k个方案与其正理想解的距离的上界.

(4)使第k个方案处于劣势的情形,其与相应的负理想解的下界的距离为

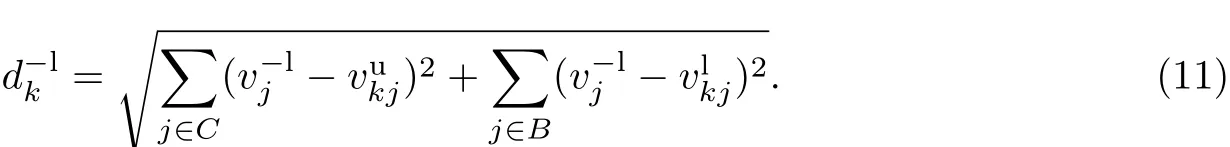
该值表示第k个方案与其负理想解的距离的下界.

2.4 计算每个方案与其理想解相对接近程度的范围

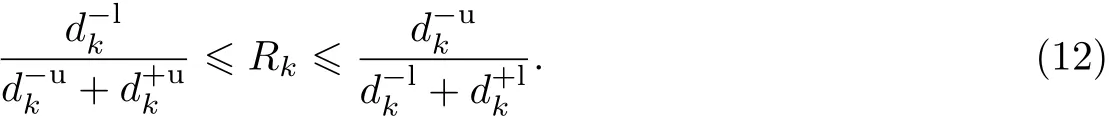
2.5 方案排序

定义2对于区间数A=[al,au],B=[bl,bu].如果m(A)≤m(B),那么区间数A劣于区间数B,记作A≺B,其中

定义3 I为一区间集,A=[al,au],B=[bl,bu]为区间集I上的区间数.在I上定义可接受函数A:I×I→[0,∞),则

由定义2和定义3可知,只需计算A(Ri≺Rj),i,j=1,2,···,m,i/=j就可以得到方案间的排序.

3 算例分析

以表1的micro-CHP方案的评价指标为例,从可持续发展的角度比较4个方案满足小型建筑供能的优劣程度.

首先,对各方案的语言信息指标采用模糊三角数形式进行量化,本工作以“很好(VH)”“好(H)”“一般(M)”“差(L)”“很差(VL)”来对三角模糊数进行量化,其中VL=(0,0,0.3),L=(0, 0.3,0.5),M=(0.3,0.5,0.7),H=(0.5,0.7,1.0),VH=(0.7,1.0,1.0).语言信息指标量化处理后的属性值如表4所示.

表4 语言信息指标量化处理后的属性值Tab le 4 Quantified linguistic information criteria values

然后,采用文献[14]提出的基于乐观-悲观指数的期望值算子将相应的三角模糊数进一步转化为实数值:三角模糊数~γ=(r1,r2,r3).在表1的多方案评价中r1≥0,则对应的确定值为

这里的λ即为乐观-悲观指数,反映了决策者对不确定性的态度,本算例取λ=0.5.

在多属性决策中,指标权重的确定是整个评价过程的关键.权重是某一属性在评价体系中所起作用大小和相对重要程度的体现.权重的合理与否直接关系到评价结果的正确程度.已有一系列的研究探讨了这一问题[15-17].本工作认为,对于建筑micro-CHP而言,技术属性、经济属性、环境属性、社会属性的权重需要根据决策的目标来确定.每一个micro-CHP项目都具有唯一性,决策的要求存在差异,需要通过具体分析其所处的环境来确定权重.算例分析暂且将9个属性值等值化,因此式(9)的ωj=1/9,j=1,2,···,9.规范化处理后的属性值如表5所示.

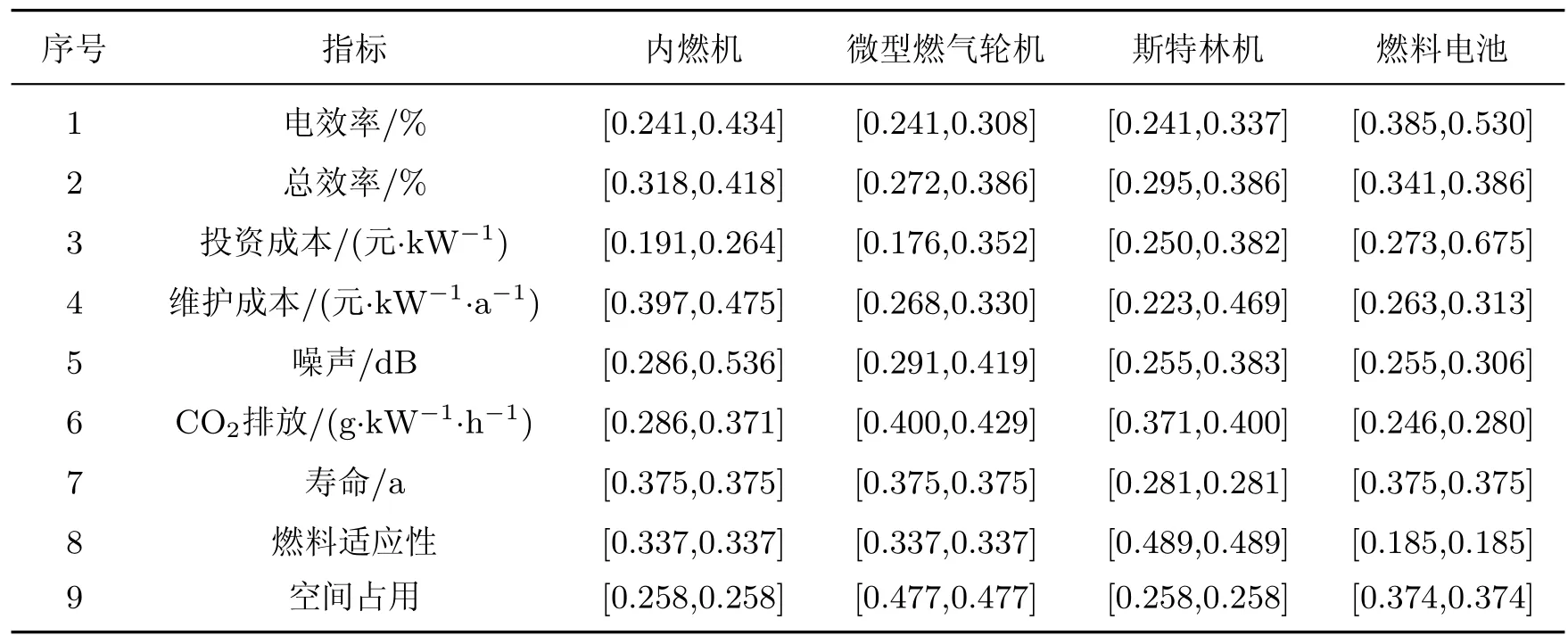
表5 规范化处理后的属性值Tab le 5 Normalized criteria values

按照式(4)～(7)计算各个方案的理想解,其中微型燃气轮机的理想解如表6所示.再按照式(8)～(11)计算每个方案到其相应的理想解的距离,其中微型燃气轮机的=0.317,

表7为按照式(12)和(13)计算得到的每个方案与其理想解相对接近程度的范围,以及方案排序.可见,微型燃气轮机为建筑micro-CHP最优方案.

表6 微型燃气轮机的理想解Tab le 6 Ideal solutions for micro-turbine

表7 与理想解的相对接近程度和排序结果Tab le 7 Relative closeness to the ideal solutions and the final ranking

式(13)提供了一种方案排序方法.定义中点m(E)为相对接近程度区间E的近似值,半宽w(E)为相对接近程度区间E的不确定性值.如果m(E)

从表7可以看出,内燃机、微型燃气轮机、斯特林机的相对接近程度值较为相似,这是因为三者都存在热力学循环过程,都受卡诺循环的限制,技术原理相似.燃料电池是一种电化学的发电装置,转换效率较高,在某些国家是micro-CHP的主力推广机型.但燃料电池在本方案排序中处于劣势,与其他三个方案存在一定的区分度,主要原因是其投资成本较高,燃料适应性差.燃料电池被称为是继水力、火力、核能之后的第四代发电装置和替代内燃机的动力装置.国际能源界预测,燃料电池是21世纪最有吸引力的发电方式之一,因此有必要对其加大资金投入,并加以政策扶持,以期使其快步进入燃料电池规模发电的先进行列.

以上的算例结果证明,用理想解区间计算距离范围、相对接近程度的方法恰当度量了区间信息的不确定性,相对于实数值理想解,在很大程度上降低了决策信息的损失.同时针对相对接近程度区间所定义的可接受函数,可以区分出方案的优劣,得出相对合理的决策结果.

Micro-CHP项目在规划阶段存在较大的方案优化空间,选择具有优势的方案是项目建设成功的前提.本工作所比较的内燃机、微型燃气轮机、斯特林机和燃料电池目前正处于研究、试验或者商业化进程起步阶段,属于“新颖”技术并缺乏长期的运行数据.另外,因为竞争原因导致的数据不公开,使得各个方案的指标存在许多不确定性,因而不可能在项目伊始就排序得到一个非常正确的方案.随着micro-CHP项目实施的不断深入,方案指标也将逐步具体和深化,使得多属性决策成为由粗到细、准确度由低到高的不断完善的过程.

4 结束语

Micro-CHP被认为是建筑节能减排的发展方向之一,适合于小型建筑的大部分是基于内燃机、微型燃气轮机、斯特林机和燃料电池方案的系统.本工作研究了项目规划阶段方案属性值为区间数时的决策问题.通过借鉴已有的TOPSIS理论和方法,提出用理想解区间来计算每个方案到其相应的理想解的距离范围、相对接近度,并采用可接受函数对几种micro-CHP方案进行排序.算例分析验证了本方法的可行性和适用性.由于micro-CHP在规划、可行性研究、初步设计阶段的项目边界条件不断明晰,因此在实际使用本工作提出的方法时可根据资料完备程度修正和完善评价指标,使得评价结论更趋准确.

尽管如此,区间数TOPSIS还需要从多方面进行研究,例如:区间数运算可能导致不确定性的增加;通常的区间数认为的区间内取值机会均等并不满足很多实际问题等.这些问题可在下一步的工作中继续研究.

[1]清华大学建筑节能研究中心.中国建筑节能年度发展研究报告2015[M].北京:中国建筑工业出版社,2015:3-5.

[2]谢德平,李显贵,潘仕梁.微型冷热电三联产发展综述[J].装备制造技术,2011(2):102-104.

[3]BARBIERIE S,SpINAP R,VENTURINIM.Analysis of innovativemicro-CHP systems to meet household energy demands[J].Applied Energy,2012,97:723-733.

[4]JAHANSHAHLOO G R,HOSSEINZADE L,IZADIKHAH M.An algorithmic method to extend TOPSIS for decision-making problems with interval data[J].Applied Mathematics and Computation,2006,175(2):1375-1384.

[5]JAHANSHAHLOO G R,LOTFIF H,DAVOODIAR.Extension of TOPSIS for decision-making problemswith intervaldata:intervaleffi ciency[J].Mathematicaland Computer Modeling,2009, 49(5/6):1137-1142.

[6]SAYADIMK,HEYDARIM,SHAHANAGHIK.Extension of VIKOR method for decision making problemwith interval numbers[J].Applied Mathematical Modelling,2009,33(5):2257-2262.

[7]YUE Z L.An extended TOPSIS for determining weights of decision makers with interval numbers[J].Know ledge-Based Systems,2010,24(1):146-153.

[8]张英俊,马培军,苏小红,等.属性权重不确定条件下的区间直觉模糊多属性决策[J].自动化学报, 2012,38(2):220-228.

[9]DYMOVAL,SEVASTJANOV P,T IKHONENKO A.Adirect interval extension of TOPSIS method[J].Expert Systems with Applications,2013,40(12):4841-4847.

[10]LIU S,CHAN F T S,RAN W.Mu lti-attribute groupdecision-making with multi-granularity linguistic assessment information:an improved approach based on deviation and TOPSIS[J]. Applied Mathematical Modelling,2013,37(24):10129-10140.

[11]华贲.从燃煤热电联产到天然气冷热电联供——中国工业和建筑物从一次能源到终端利用模式的战略转型[J].中外能源,2011,16(11):25-30.

[12]金炼,张亚君,杨尚恒,等.家庭用微型热电联产技术[J].现代化工,2012,32(5):6-15.

[13]国家发展改革委经济运行调节局,国家电网公司营销部,南方电网公司市场营销部.分布式能源与热电冷联产[M].北京:中国电力出版社,2013:24-46.

[14]ZENG Z Q,NASRI E,CHINIA,et al.Amultiple ob jective decision makingmodel for energy generation portfolio under fuzzy uncert ainty:case study of large scale investor-owned utilities in Florida[J].Renewable Energy,2015,75:224-242.

[15]吴大为.分布式冷热电联产系统的多目标热力学优化理论与应用研究[D].上海:上海交通大学, 2008:43-46.

[16]CHATZIMOURATIDISAI,PILAVACHIP A.Technological,economic and sustainability evaluation of power plants using the analytic hierarchy process[J].Energy Policy,2009,37(3):778-787.

[17]PILAVACHIP A,STEpHANIDISSD,PAppASV A,et al.Mu lti-criteria evaluation ofhydrogen and natural gas fuelled power plant technologies[J].Applied Thermal Engineering,2009,29(11/12): 2228-2234.

Sorting TOPSIS of interval data for micro-CHP in bu ild ings

RUAN Hongquan1,2,GAO Xin1,TAN Lijun3
(1.School of Economics and Management,Tongji University,Shanghai 200092,China; 2.ENN Energy Service(Shanghai)Co.,Ltd.,Shanghai 200082,China; 3.College of Sciences,Shanghai University,Shanghai 200444,China)

Micro-combined heat and power(micro-CHP)helps to improve energy efficiency and protect environment,thus becoming a trend in the building energy supply.In the planning stage of a micro-CHP pro ject,evaluation of the design scheme is a key to success.To apply interval data criteria of the scheme to technique for order preference by similarity to an ideal solution(TOPSIS),the distance range and relative closeness are calculated using the interval ideal solution.An acceptability function is defined to in sort schemes.An example of 4 alternatives suitable for small buildings is presented to show feasibility and practicability of themethod.

micro-combined heat and power(micro-CHP);mu lti-criteria decision; interval data;technique for order preference by similarity to an ideal solution(TOPSIS)

F 062.9;F 272.3

A

1007-2861(2017)04-0636-11

DO I:10.12066/j.issn.1007-2861.1712

2015-09-06

阮红权(1977—),男,工程师,博士,研究方向为城市管理与建设工程管理、分布式能源规划与管理.

E-mail:1110256@tongji.edu.cn