基于多元相场理论的细菌生物膜生长动力学建模及其数值模拟
2017-09-19张曙梅徐向荣徐浩周涛李双李妍
张曙梅,徐向荣,徐浩,周涛,李双,李妍
(1.安徽工业大学机械工程学院,安徽马鞍山243032; 2.安徽工业大学数理学院,安徽马鞍山243032)
基于多元相场理论的细菌生物膜生长动力学建模及其数值模拟
张曙梅1,徐向荣1,徐浩2,周涛1,李双1,李妍1
(1.安徽工业大学机械工程学院,安徽马鞍山243032; 2.安徽工业大学数理学院,安徽马鞍山243032)
细菌生物膜普遍存在于自然界和工业环境中.将细菌生物膜视为由多种组元组成的不可压缩的黏性流体,结合多元相场理论、物质连续方程、动量守恒方程、溶质场控制方程和生物反应动力方程对细菌生物膜生长动力学进行建模.通过对模型的数值模拟,可以描述细菌和胞外聚合物在静态环境和动态环境中的生长状况以及营养物质的消耗规律.
细菌生物膜;相场理论;动力学模型;数值模拟
细菌生物膜是单一或多种细菌为了适应自然环境而形成的微菌落聚集物,其主要成分为多糖蛋白复合物[1-2].细菌生物膜的生长是一个产生、发展、壮大的过程.通过对细菌生物膜生长规律的研究以及建立细菌生物膜生长动力学模型,既可以揭示细菌生物膜的生长机理,又可以有效控制细菌生物膜的形成和发展,抑制其有害作用[3].已有的研究主要是从数学、流体力学、计算机仿真以及实验的角度对细菌生物膜进行研究,具体可分为低维连续模型、有限扩散凝聚模型、元胞自动机模型和单流体相场模型[4-9].本工作的研究内容是属于单流体相场模型的范畴.相场理论以Ginzburg-Landau理论为物理基础,通过微分方程来体现具有特定物理机制的扩散、有序化势和热力学驱动的综合作用,通过计算机编程求解上述方程,从而获取研究体系在时间和空间上的瞬时状态[10-11].Cogan等[12-13]提出的模型是将细菌生物膜看作由胞外聚合物和等效溶剂组成的生物凝胶体.由于渗透压的作用,生物凝胶体吸收或排除溶剂导致其膨胀或收缩.因此,影响细菌生物膜形态的物理化学因素主要是渗透压.但在细菌生物膜内,细菌和胞外聚合物均属于高分子,渗透压不仅作用于胞外聚合物上,而且也作用在细菌上.因此,仅考虑渗透压对胞外聚合物的作用是不合理的.Zhang等[14-15], Brandon等[16]和Chen等[17]在Cogan研究的基础上提出了新的模型,将细菌生物膜视为不可压缩的多组元混合流体,主要考虑细菌生物膜中胞外聚合物、细菌和等效溶剂(营养物质和水)的体积分数的变化.但此模型只考虑了混合自由能密度梯度、流体的静压力以及剪切力对细菌生物膜的作用,忽略了细菌生物膜内各组元的摩擦阻力的作用,以及渗透压对细菌生物膜生长的影响.
鉴于上述模型的不足,本工作提出了一种单流体二组元的细菌生物膜生长动力学模型.本模型既考虑了细菌生物膜内部生物质的分布不均匀性,又考虑了渗透压、摩擦阻力和流体剪力对细菌生物膜生长的影响.在本工作模型中,仍将整个细菌生物膜系统近似认为是不可压缩的,并且假设细菌生物膜是由胞外聚合物、细菌和等效溶剂(营养物质和水)组成,侧重考虑了渗透压、流体剪力以及不同组元之间摩擦阻力的作用.通过对建立的多组元细菌生物膜生长动力学模型的数值求解,模拟了静态和动态环境中细菌生物膜膜内细菌、胞外聚合物的体积分数变化,以及营养物质浓度在空间上的分布规律和流体剪力对细菌生物膜生长的影响.静态环境,即细菌生物膜系统的体积平均速度为0,vx=0.例如,存有静态液体的管道和容器、实验室用于培养细菌生物膜的培养皿和潮湿的载体表面等都属于细菌生物膜生长的静态环境.细菌生物膜在此环境中生长,其膜内的胞外聚合物、等效溶剂和营养物质主要通过扩散作用进行物质传输以及生物化学反应.动态环境,即细菌生物膜系统的体积平均速度不为0,vx/=0.例如,存有流动液体的管道、污水处理池、受流水冲击的岩石表面以及任何动物的血管壁等都属于细菌生物膜生长的动态环境.当细菌生物膜在动态环境中生长时,膜内的聚合物网状结构、等效溶剂和营养物质主要通过对流-扩散共同作用进行物质传输以及生物化学反应.由于在静态环境和动态环境中细菌生物膜系统的物质传输机理是不一样的,因此其在这两种条件下的生长是存在差异的.
1 模型的建立
本工作将细菌生物膜视为由多种组元组成的黏性流体,即细菌、胞外聚合物和等效溶剂,并运用多元相场理论对细菌生物膜生长动力学进行建模.
1.1 多元细菌生物膜系统的动量方程
设φp为胞外聚合物的体积分数,ϕb为细菌的体积分数,ϕs为等效溶剂的体积分数,vp为胞外聚合物的速度,vb为细菌的速度,vs为等效溶剂的速度,ρp为胞外聚合物的密度,ρb为细菌的密度,ρs为等效溶剂的密度.由Navier-Stokes方程得
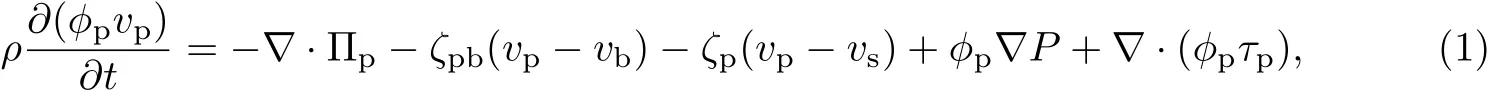
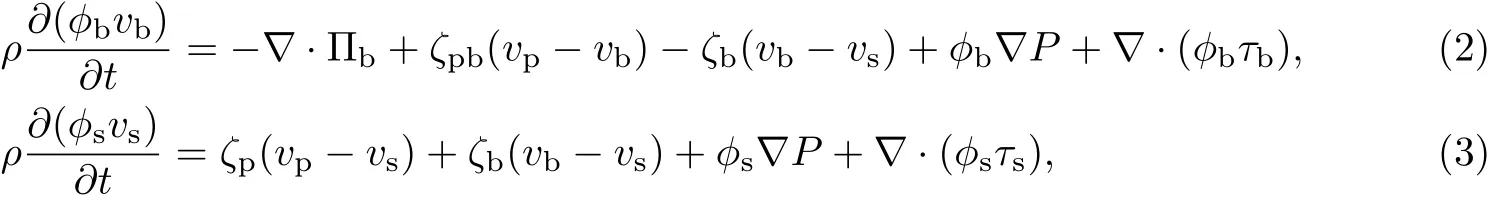
式中,Πp为作用于胞外聚合物上的渗透压,Πb为作用于细菌上的渗透压;ζpb为胞外聚合物和细菌之间的体积摩擦阻力系数,ζp为胞外聚合物和等效溶剂之间的体积摩擦阻力系数,ζb为细菌和等效溶剂之间的体积摩擦阻力系数,ρ为细菌生物膜中胞外聚合物、细菌和等效溶剂的体积平均密度,且ρ=ϕpρp+ϕbρb+ϕsρs,P为作用于整个细菌生物膜上的液体静压力,τp为胞外聚合物的应力,τb为细菌的应力,τs为等效溶剂的应力.
将式(1)~(3)相加可得
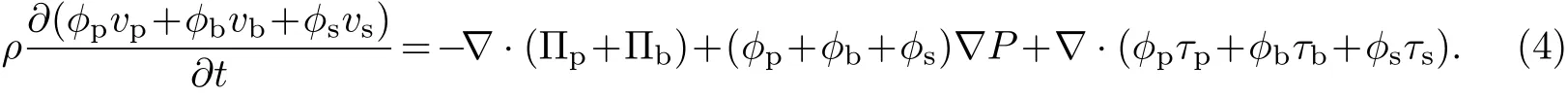
由ϕp+ϕb+ϕs=1可得令
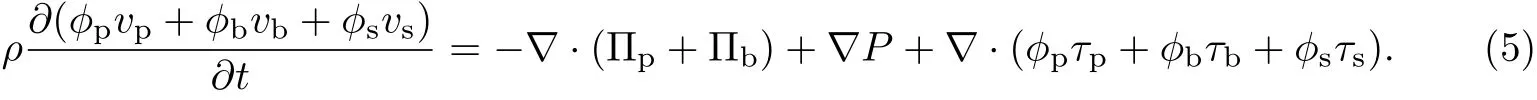
细菌生物膜的体积平均速度v=ϕpvp+ϕbvb+ϕsvs,则式(5)可以改写为
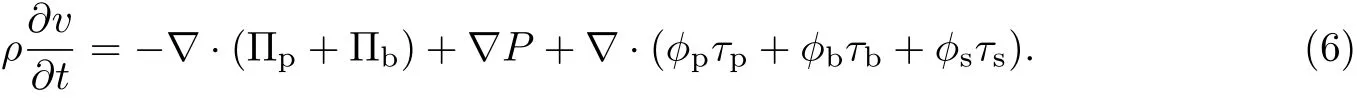
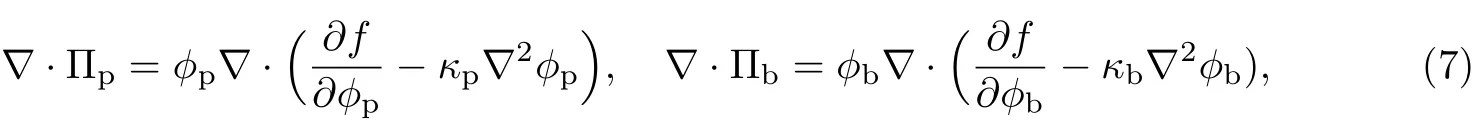
式中,κp为胞外聚合物的Ginzburg-Landau常数,κb为细菌的Ginzburg-Landau常数.将式(7)代入式(6)可得
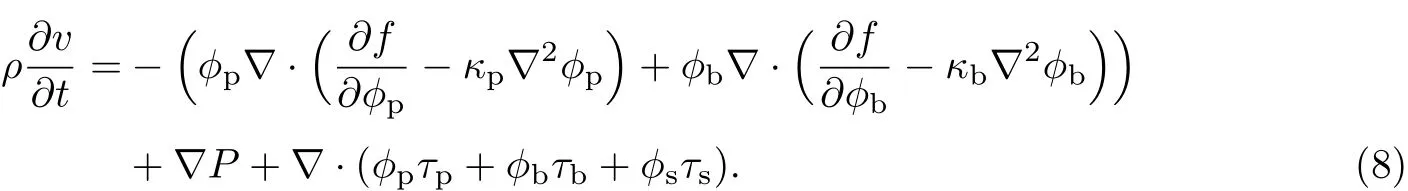
由广义Flory-Huggins混合自由能理论[19]可知:
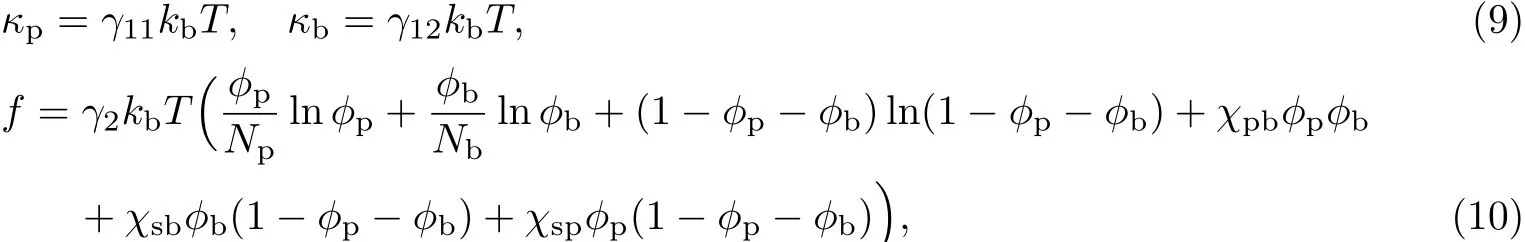
式中,γ11,γ12分别为胞外聚合物和细菌畸变能系数,γ2为混合自由能系数,T为温度.
1.2 多组元细菌生物膜系统的连续方程
连续方程是质量守恒定律对于运动流体的表达,由欧拉连续方程的微分形式可得


在黏性流体中,∇·v表示流体速度的散度.由式(12)可知,细菌生物膜中胞外聚合物、细菌和等效溶剂的体积平均速度v为无散度平均速度场.
1.3 胞外聚合物、细菌和等效溶剂的输运方程(相场控制方程)
胞外聚合物、细菌和等效溶剂的传质过程可以运用多元相场理论来描述.由Hohenberg等[20]提出的相场控制方程可得如下方程.
(1)胞外聚合物的输运方程为
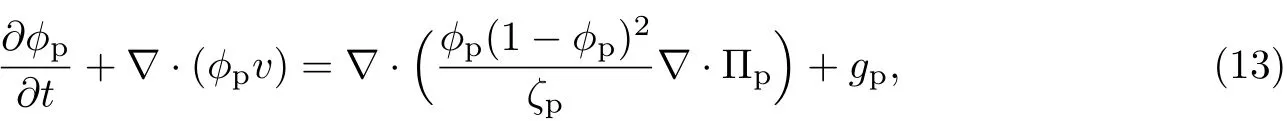
式中,gp为胞外聚合物的生长率. (2)细菌的输运方程为
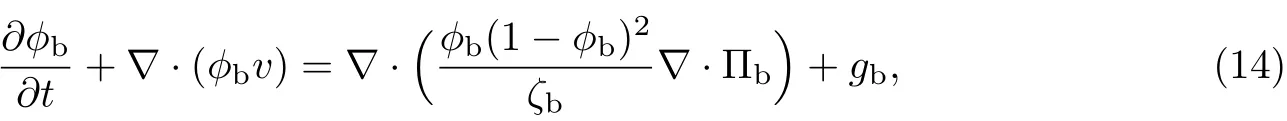
式中,gb为细菌的生长率.
(3)等效溶剂的输运方程为
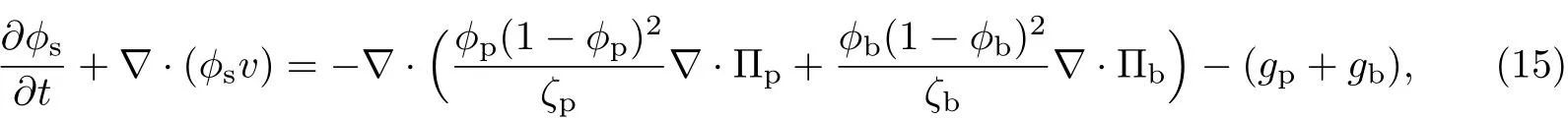
式中,ζp为胞外聚合物和等效溶剂之间的体积摩擦阻力系数,ζb为细菌和等效溶剂之间的体积摩擦阻力系数,且二者分别是胞外聚合物、细菌和等效溶剂体积分数的函数,即ζp=ζp(ϕp,ϕb,ϕs),ζb=ζb(ϕp,ϕb,ϕs).分别取ζp=ζ0ϕp(1-ϕp),ζb=ζ0ϕb(1-ϕb),则胞外聚合物的输运方程可改写为
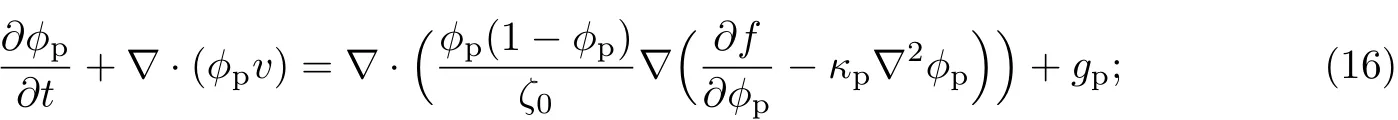
细菌的输运方程可改写为
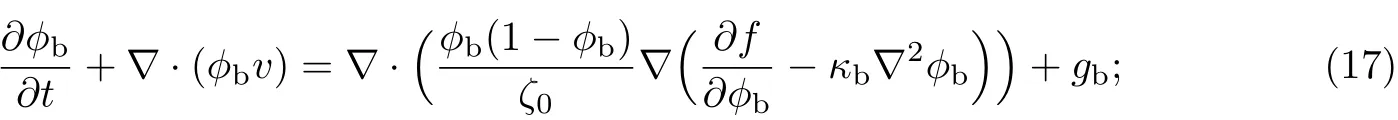
等效溶剂的输运方程可改写为
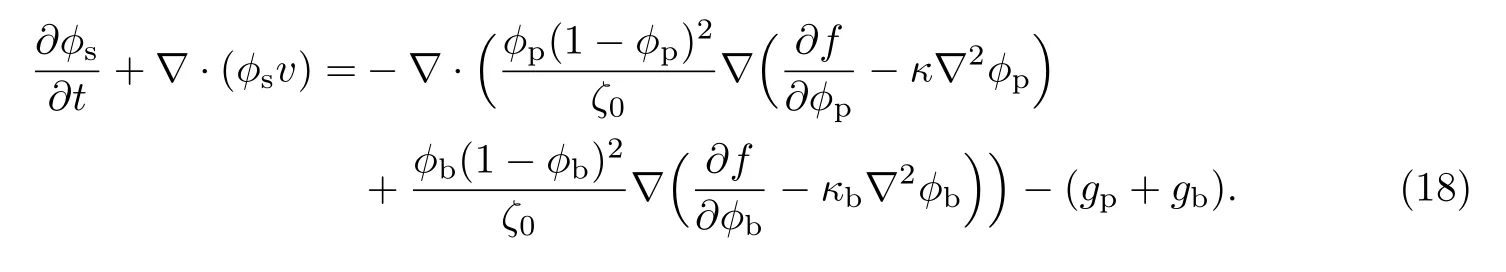
1.4 营养物质的输运方程(溶质场控制方程)
营养物质的存在是细菌生物膜生长的必要条件,外界营养物质在渗透压的作用下透过细菌生物膜传输到膜内被细菌所消耗,为其提供充足的生长条件.营养物质在细菌生物膜系统中的传质过程可以运用对流-扩散反应方程[21]来描述,即
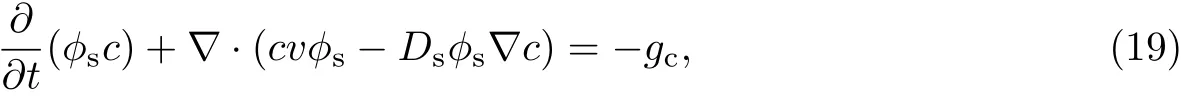
式中,c为营养物质的浓度,Ds为营养物质的扩散系数,gc为营养物质的消耗率.
1.5 多组元细菌生物膜中各组元的生物反应动力学
Monod方程常被用来描述生物的生长速率与基质浓度的关系[22].因此,运用Monod方程可以得到胞外聚合物、细菌生长率以及营养物质消耗率的表达式.
(1)胞外聚合物的生长率为
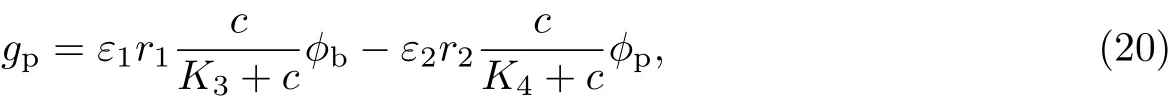
式中,r1为胞外聚合物的最大生长率,r2为胞外聚合物的最大消耗率,K3,K4,K5均为半饱和常数,ε1和ε2均为反应动力学方程的尺度参数.
(2)细菌的生长率为
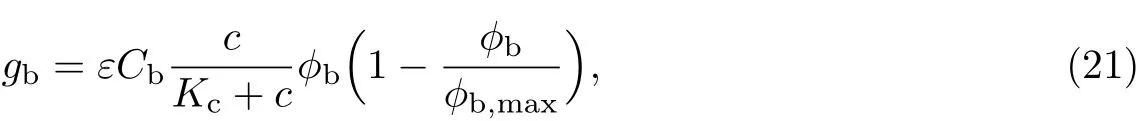
式中,Cb为细菌的最大生长率,ε为反应动力学方程的尺度参数,ϕb,max为细菌体积分数的最大容量,Kc为半饱和常数.
(3)营养物质的消耗率为

式中,Ac为营养物质的最大消耗率,K1为半饱和常数.
1.6 本构方程
本构方程是反映物质宏观性质的数学模型,主要描述应力和应变率或应力张量与应变张量之间的函数关系.本工作将细菌生物膜中的胞外聚合物、细菌和等效溶剂均视为不可压缩的广义黏性牛顿流体,因此运用广义牛顿流体的本构方程可以分别描述胞外聚合物、细菌和等效溶剂的应力.由于本工作主要考虑细菌生物膜在平均速度场中的生长,因此胞外聚合物、细菌和等效溶剂的应变率张量将运用平均应变率张量表示.由广义牛顿流体的本构方程可得
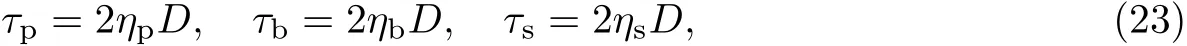
2 数值求解与模拟
2.1 一维动力学模型
由于细菌生物膜的形状比较复杂,大体呈“蘑菇”状,这对细菌生物膜生长动力学方程边界条件的确定以及方程的数值求解带来困难.经实验测定,大部分细菌生物膜的厚度在1~2 mm范围[23]内,因此,细菌生物膜生长动力学方程的生长尺度较小,可以将其截面形状等效为Hz×L矩形,如图1所示.
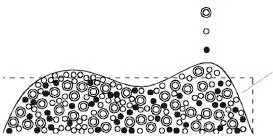
图1 多组元细菌生物膜的截面形状等效图F ig.1 Equivalent figure ofmulticomponent bacterial biofi lm’s cross section shape
本工作主要研究多组元细菌生物膜沿载体垂直向上方向(z方向)的生长,即确定多组元细菌生物膜的生长动力学方程在z∈[0,Hz]区域的数值解.细菌生物膜内生物质在x和y方向的生长和物质传输可以认为是均匀进行的,因此多组元细菌生物膜生长动力学方程的所有变量均是(z,t)的函数,即ϕp=ϕp(z,t),ϕb=ϕb(z,t),vx=vx(z,t),c=c(z,t).
基于此,多组元细菌生物膜生长动力学方程可以简化为一维动力学方程,即
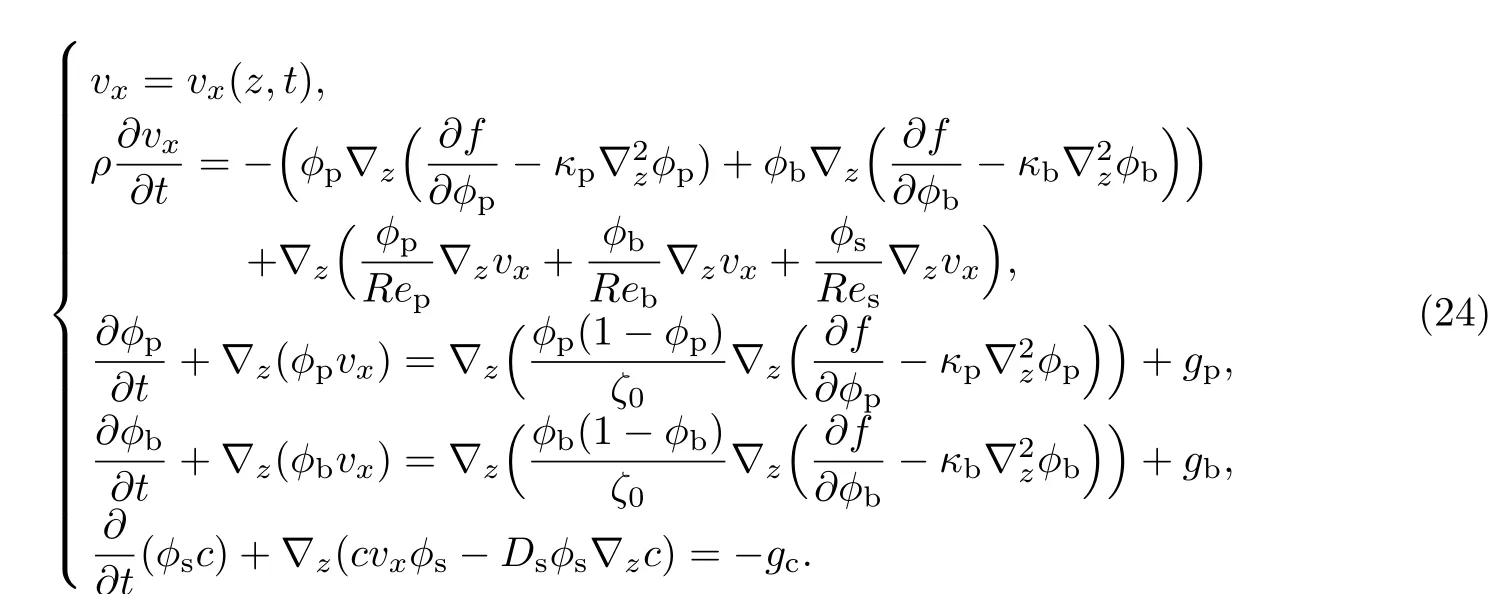
多组元细菌生物膜一维生长动力学方程的边界条件为
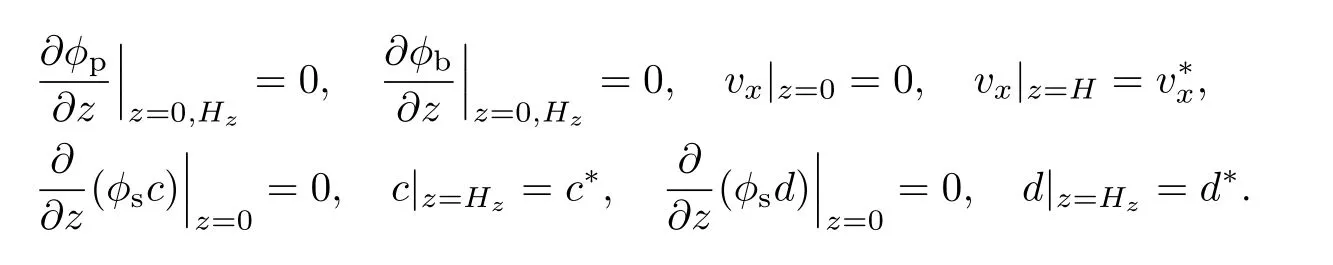
多组元细菌生物膜一维生长动力学方程的初始条件为
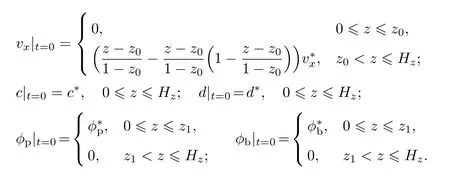
表1列出了多组元细菌生物膜生长动力学数值模拟所需的物性参数.

表1 多组元细菌生物膜系统的物性参数Tab le 1 Physical parameters ofmulticomponent bacterial biofi lmsystem
2.2 多组元细菌生物膜生长动力学方程的求解
在对多组元细菌生物膜生长动力学进行模拟时,关键步骤是对动力学方程进行数值求解.数值计算的实质就是将动力学方程对时间和空间进行一定形式的离散化处理,然后结合方程的初始条件及边界条件对离散后的方程进行迭代求解.本工作基于Crank-Nicolson有限差分格式求解细菌生物膜生长动力学方程.该方法是属于对偏微分方程求解的加权隐式方法中的一种[24].多组元细菌生物膜生长动力学模型求解系统的前处理和数值计算程序实现的流程如图2所示.
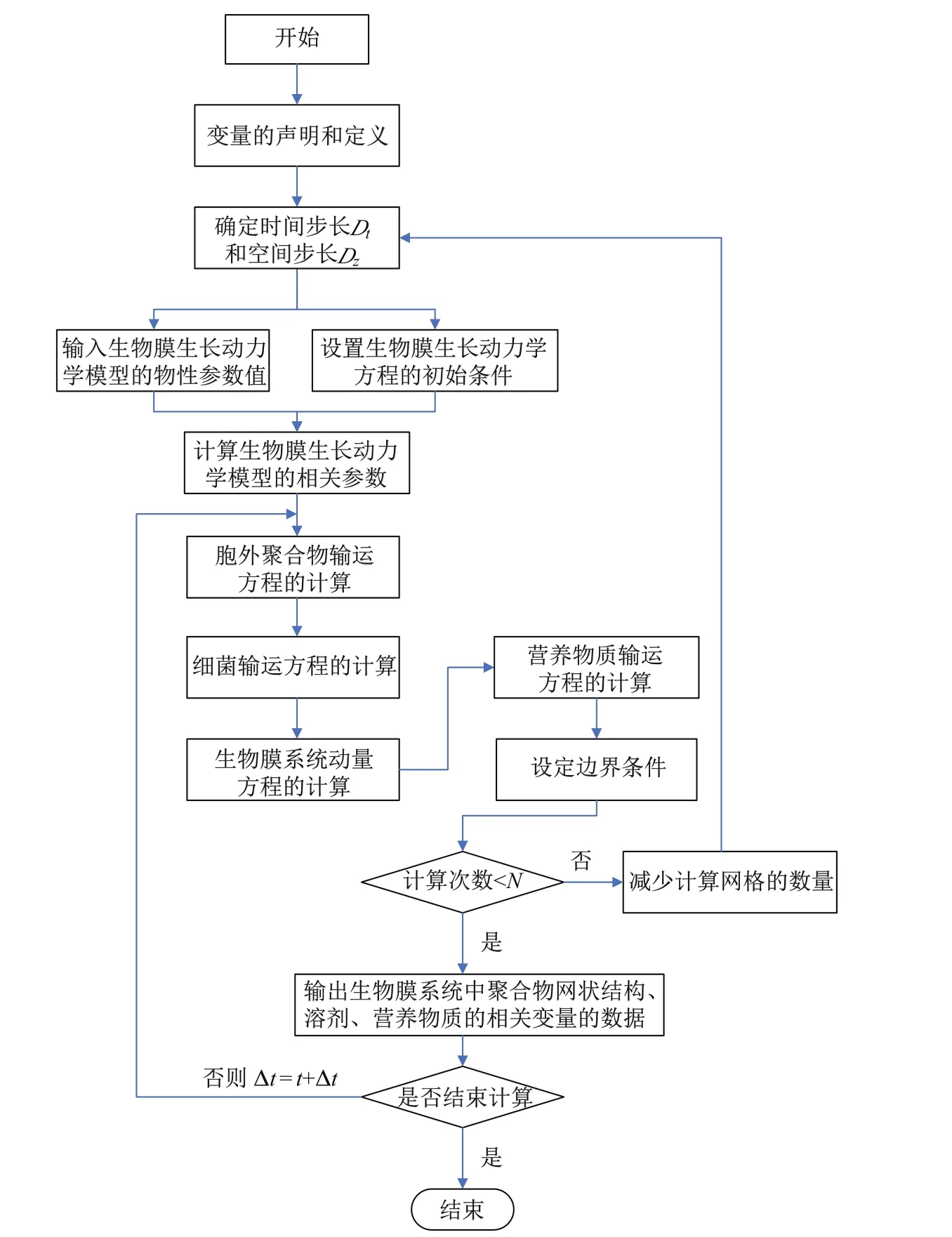
图2 多组元细菌生物膜生长动力学模型求解系统的前处理和数值计算程序流程图Fig.2 Flow chart of themulticomponent bacterial biofi lmgrow ing dynamicalmodel’s solving systemof pretreatment processing and numerical calculation program
3 多组元细菌生物膜在静态环境和动态环境中的生长
本工作结合多组元细菌生物膜生长动力学模型的数值模拟结果,分析比较了静态和动态环境中细菌生物膜胞外聚合物的体积分数和营养物质浓度在24~96 h(1~4 d)的分布情况,以及两种条件之间的差异.
图3和4是不同时刻胞外聚合物和细菌的体积分数在静态和动态环境中的分布曲线,其中初始时刻t=0.由图可知,胞外聚合物和细菌的体积分数及其分布空间在两种环境中均随着时间的增加而不断增大,但在载体附近,静态环境中胞外聚合物和细菌的体积分数均大于动态环境,且二者的差值随着时间的增加而增大.这是由于动态环境中胞外聚合物和细菌在对流-扩散的共同作用下传质速度较快、传质阻力小,胞外聚合物和细菌能迅速地向无膜区域传输,从而使得动态环境中载体附近的胞外聚合物和细菌的体积分数较小.动态环境中胞外聚合物和细菌的体积分数的分布空间均大于静态环境,且二者的差值也是随着时间的增加而增大.during diff erent time
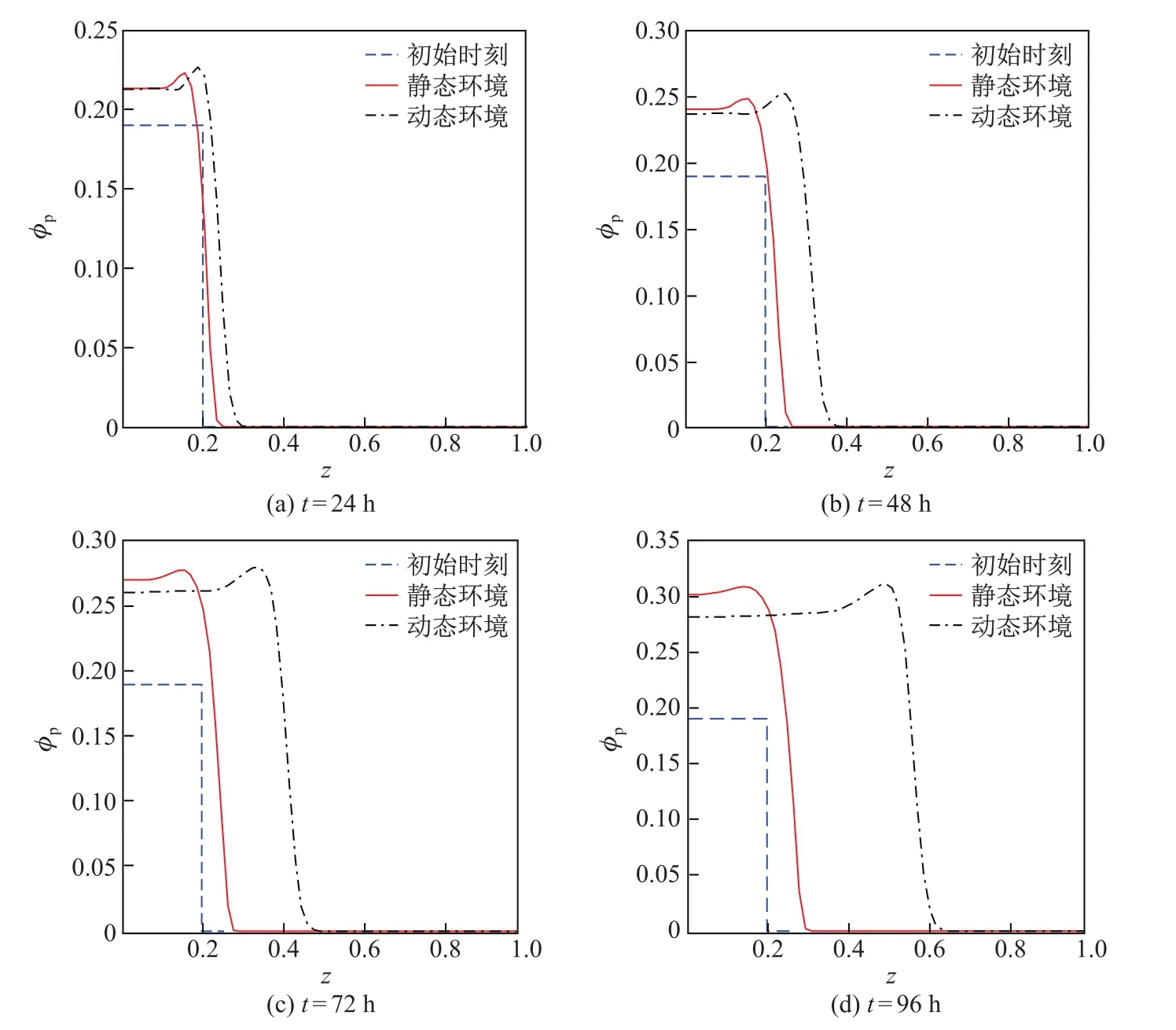
图3 不同时刻,胞外聚合物体积分数在静态环境和动态环境中的分布对比曲线Fig.3 Distribution curves of the extracellu lar polymer’s volume fraction in the static and dynamic environments during diff erent time
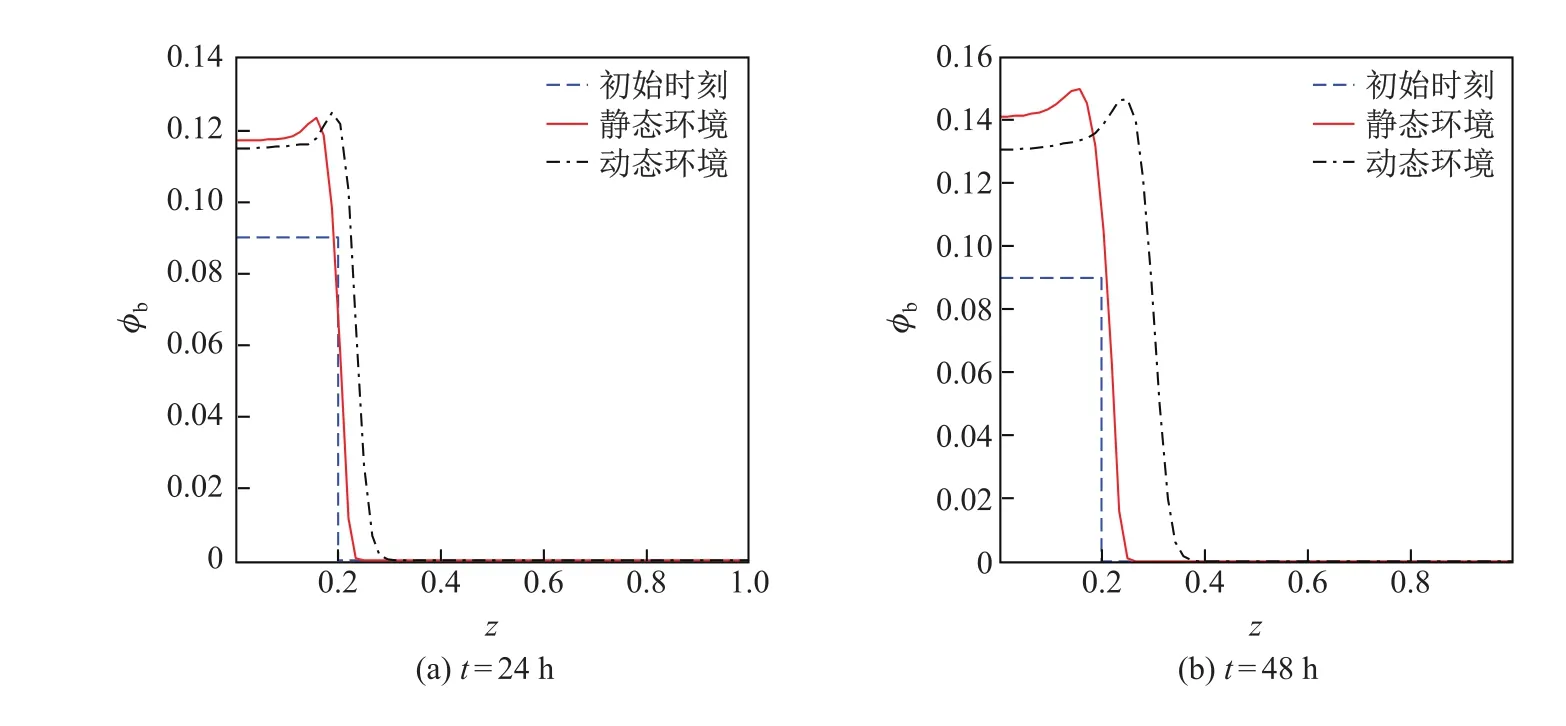
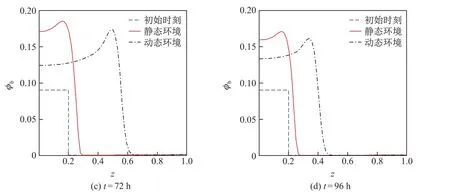
图4 不同时刻,细菌体积分数在静态环境和动态环境中的分布对比曲线Fig.4 Distribution curves of the bacteria’s volume fraction in the static and dynamic environments
这说明动态环境中细菌生物膜厚度增长较快.通过对比可知,动态环境更适合细菌生物膜的生长,并且膜内物质的对流传质过程是促进细菌生物膜生长的主要因素.
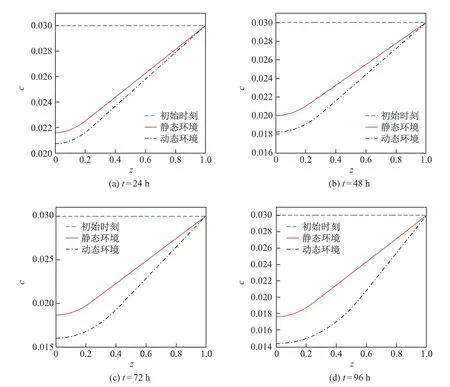
图5不同时刻营养物质浓度在静态环境和动态环境中的分布对比曲线Fig.5 Distribution curves of the nutrients’concentration in the static and dynamic environments during diff erent time
图5 为不同时刻营养物质浓度在静态环境和动态环境中的分布曲线,其中初始时刻t=0.由图可知,两种环境中载体附近营养物质浓度的分布曲线呈非线性,而远离载体处的分布曲线可以近似认为呈线性,且直线的斜率随着时间的增加而增大.同一时刻动态环境中营养物质消耗较多,营养物质的浓度下降较快,浓度差值随着时间的增加而增大,且远离载体处营养物质浓度梯度较大.通过对比可知,对流-扩散传质过程促进营养物质的传输和消耗,使得细菌生物膜获取的营养物质更多,生长速率更快.
4 结论
本工作主要运用多元相场理论控制方程,并结合物质连续方程和动量守恒方程建立了耦合流场的相场模型,并且添加溶质场控制方程和生物反应动力方程,对细菌生物膜生长动力学进行了综合建模.对建立的动力学模型进行了一维数值模拟,得到如下结论.
(1)细菌生物膜在静态和动态环境中生长时,胞外聚合物和细菌的体积分数,以及营养物质浓度在空间上的分布规律均是相似的.载体附近营养物质浓度呈非线性分布,而远离载体处营养物质浓度呈近似线性分布.
(2)动态环境中胞外聚合物、细菌和营养物质通过对流-扩散作用进行传质,加快了细菌生物膜的生长.动态环境更适合细菌生物膜的生长,并且膜内物质的对流传质过程是促进细菌生物膜生长的主要因素.
(3)本工作模型在已有模型的基础上进行改善,考虑了渗透压、摩擦阻力等多种因素对生物膜生长的影响,且与现实生活中生物膜生长情况以及国内外的实验结果相一致.这也充分反映了本模型的可行性.
[1]杨朵,张正.细菌生物膜及其相关研究进展[J].中国实验诊断学,2007,11(10):1416-1422.
[2]MARTIN K,MARTINAH,H ANS-J OACHMI B,et al.Automated con focal laser scanningmicroscopy and semia-automatedmiage processing for analysisofbiofi lms[J].Appl Environ Microbiol,1998, 64:4115-4124.
[3]陈黎明,柴立和.生物膜动力学的研究现状与展望术[J].力学进展,2005,35(3):411-416.
[4]尚倩倩,方红卫,何国建.水利工程中的生物膜研究进展[J].中国科技论文在线,2010,5(7): 563-568.
[5]F LEMMING H C,W INGENDER J,MAYER C,et al.Cohesiveness in biofi lmsmatrix polymers[J]. J Theor Biol,2009,253:689-708.
[6]任伟.不同清洗剂及其不同作用时间对内镜生物膜清除的实验研究[D].广州:南方医科大学,2011.
[7]李鹏.尾端缝线双J管细菌学检测的临床意义[D].苏州:苏州大学,2012.
[8]ANGUIGE K,K ING J R.Mathematical modeling of therapies targeted at bacterial quorumsensing[J].Mathematical Biosciences,2004,19:239-283.
[9]李亮亮,徐向荣,周涛,等.生物膜数学建模的发展[J].广东化工,2013,40(19):64-65.
[10]MOELANS N,B LANpAIN B,W OLLANTS P.An introduction to phase-field modeling of microstructure evolution[J].Computer Coupling of Phase Diagrams and Thermochemistry,2008,32: 268-294.
[11]吕冬兰.流场作用下合金枝晶生长的相场法数值模拟[D].南昌:南昌航空大学,2009.
[12]C OGAN N G,K EENER J P.The role of the biofi lmmatrix in structural development[J].Math Med Biol,2004,21:147-166.
[13]C OGAN N G,K EENER J P.Channel formation in gels[J].SIAMJ Appl Math,2004,65:1839-1854.
[14]Z HANG T,C OGAN N C,W ANG Q.Phase-field models for biofi lmsⅠ.Theory and one dimensional simulations[J].SIAMJ Appl Math,2008,69:641-669.
[15]Z HANG T,C OGAN N C,W ANG Q.Phase-field models for biofi lmsⅡ.2D numerical simu lations of biofi lm-flow interactions[J].CommComput Phys,2008(4):72-101.
[16]B RANDON L,W ANG Q,Z HANG T Y.Amulticomponent model for biofi lm-d rug interaction[J]. DCDS-B,2012,15(2):417-456.
[17]C HEN C,W ANG Q.3-D numericalsimulations ofbiofi lmflow s[J].East Asian Journalon Applied Mathematics,2011(1):197-214.
[18]AKIRAO.Phase transition dynamics[M].London:Cambridge University Press,2008.
[19]C HARLES W,E GBERT H,D ALE K,et al.How myxobacteria glide[J].Current Biology,2002, 12(6):369-377.
[20]H OHENBERG P C,H ALpERIN B I.Theory of dynamic critical phenomena[J].Rev Mod Phys, 1977,49:435-456.
[21]周光炯,严宗毅,许世雄,等.流体力学[M].北京:高等教育出版社,2000.
[22]W ANG Q,Z HANG T Y.Review ofmathematicalmodels for biofi lms[J].Solid State Communications,2010,150:1009-1022.
[23]AKIRAO.Theory of phase transition in polymer gels[D].Kyoto:Kyoto University,1992:6-10.
[24]J OHN D A.计算流体力学基础及其应用[M].吴颂平,刘赵淼,译.北京:机械工业出版社,1995.
Bacterial biofi lmgrow th dynamicalmodeling and numerical simu lation based on mu ltiple-phase field theory
ZHANG Shumei1,XU Xiangrong1,XU Hao2,ZHOU Tao1,LIShuang1,LIYan1
(1.School of Mechanical Engineering,Anhui University of Technology,Maanshan 243032, Anhui,China; 2.School of Mathematical Science and Engineering,Anhui University of Technology, Maanshan 243032,Anhui,China)
Bacteria biofi lms are w idespread in nature and industrial environments.Abacteria biofi lmis regarded as an incompressible viscous fluid composed ofmultiplecomponents.The theory of multiple-phase field,material continuity equation,momentumconservation equation,field control equations and biological reaction dynamic equation are combined tomodelbacterialbiofi lmgrow th dynamics.Anumericalsolution of themultiplecomponent bacterial biofi lmgrow th dynamical model is used to describe the grow th of bacteria,the law of nutriment’s consumption,and extracellular polymers in static and dynamic environments.
bacteria biofi lm;phase field theory;dynamicalmodel;numerical simu lation
Q 66
A
1007-2861(2017)04-0563-12
DO I:10.12066/j.issn.1007-2861.1690
2015-06-29
国家自然科学基金资助项目(31300125)
徐浩(1982—),男,讲师,研究方向为生物膜、生物计算.E-mail:ahaxuo@ahut.edu.cn
