神经网络的高反差图像增强算法研究

梁康康，李 涛

(西安邮电大学 计算机学院，陕西 西安 710121)

神经网络的高反差图像增强算法研究

梁康康，李 涛

(西安邮电大学 计算机学院，陕西 西安 710121)

针对多尺度Retinex算法在图像增强过程中存在的算法运算量大的问题，提出了将RBF神经网络作为高反差图像增强算法。该算法从训练数据集中获取以3×3为邻域像素的特征向量以及目标图像对应的特征向量，通过聚类算法来确定网络隐含层的中心向量和扩展常数，采用梯度下降法使网络快速收敛得到最优解。利用RBF神经网络建立高反差图像与增强算法之间的非线性映射关系，根据神经网络参数进行快速图像处理，从而实现图像实时处理。仿真实验结果表明，与传统的基于Retinex理论算法相比，基于神经网络的高反差图像增强算法，不仅能够改善图像边缘以及细节，而且图像的清晰度也十分明显。因此，所提出的算法是一种有效的图像增强算法，在高反差图像增强中具有较好的应用前景。

神经网络；高反差；特征向量；快速收敛；图像增强

0 引 言

图像增强，在图像处理的实际应用中起着很重要的作用。其中，高反差处理[1]尤为突出，它是对图像中感兴趣的部分采用特定技术，增强后的图像相比原图像，可以满足某些特殊分析的需要，比如图像的边缘或者纹理的加深等。在传统的图像处理中，对高反差图像的处理方法有均衡化直方图法[2]、频域和空域的增强方法、小波变换增强以及基于Retinex理论的算法等[3]。20世纪中后期，Retinex理论被提出，并得到了研究人员的重视，从使用滤波器的Retinex算法到改进的中心环绕Retinex，包括单尺度Retinex和多尺度Retinex，以及多尺度带有颜色恢复的Retinex算法[4]等。其中，基于Retinex理论的增强算法具有颜色保真、图像清晰、对比度均衡、细节增强和动态范围压缩等多方面的优势。由于这些算法在一些特殊场合存在一定的局限性和单一性，通过神经网络在图像中的应用可以达到较好的效果。

近年来，随着对神经网络理论的深入探索，神经网络模型在图像处理领域中的应用也越来越广泛。因此，在对神经网络[5]分析研究之后，它可以逼近任何连续的函数[6]，并且具有很强的泛化能力。在BP神经网络[7]训练过程中，选择的参数较多，训练速度慢，隐藏层的个数以及神经元的个数不太容易确定，导致训练好的网络的泛化能力不是很强。基于这些特性，RBF神经网络刚好克服上述缺点，且网络结构简单，训练速度快，泛化能力强。为此，采用RBF神经网络[8]，以实现高反差图像增强，通过聚类算法和梯度下降法来训练网络，取得了较好的结果，同时也具有实时对图像进行高反差处理的能力。

1 RBF网络实现图像增强

1.1RBF神经网络结构

RBF网络是一种前馈网络，一般分为3层，分别是输入层、隐含层和输出层，典型结构如图1所示。信号通过输入层节点传递到隐含层，隐含层节点由类似于高斯函数的一些函数构成，隐含层到输出层通过权值相连。RBF神经网络的隐含层是非线性的，采用径向函数作为基函数，将输入向量空间转换到隐含层空间，使得原来线性不可分的问题变得线性可分，输出层是线性的。

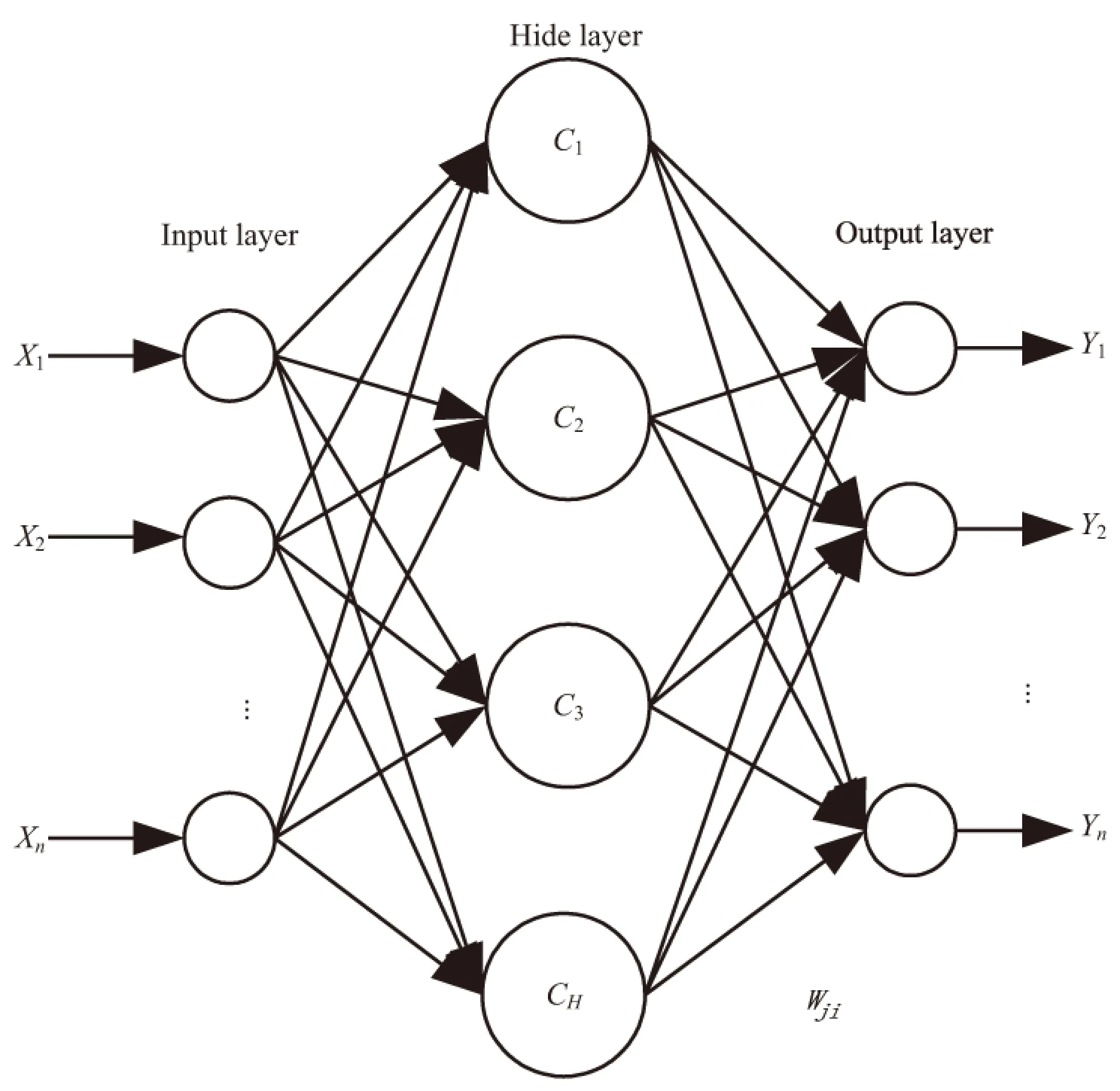
图1 RBF神经网络结构

令RBF网络结构为M-H-N(M个输入节点，H个隐含层节点和N个输出节点),则输出层第k个节点的输出为：

(1)

其中，Wjk为隐含层第j个节点到输出层第k个节点之间的权值；G为隐含层第j个节点的激活函数；H为隐藏层神经元的个数；Yk为输出层节点的输出。

RBF网络中一般选取高斯函数[9]为径向基函数(激活函数)，即

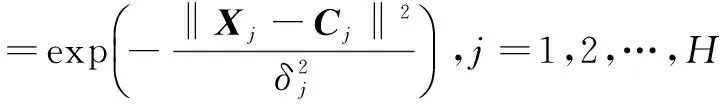
(2)

其中，Xj为网络的输入向量,即(x1,x2,…,xn)；Cj和δj为隐藏层第j个节点中高斯函数的中心矢量和宽度(扩展常数)。

1.2RBF网络的学习算法

RBF网络中需要调整的参数是隐藏层每个神经元的中心矢量和扩展常数以及隐藏层到输出层之间连接的权值。其中基函数的中心矢量和宽度决定整个网络的性能，整个过程分为无监督学习和监督学习，需要分为两个部分训练：

首先使用聚类算法来确定隐藏层各神经元的中心矢量，再由中心矢量确定扩展常数,采用的是K-means算法[10]。

(1)从训练数据中随机选取k个不同训练样本，分别作为k个簇的中心；

(2)分别计算其他样本到k个簇中心的欧氏距离，将这些样本分别划分到距离最小的簇中；

(3)根据聚类结果，通过取簇中所有样本中各自维度的平均值，得到这k个簇的中心；

(4)将全部样本按照新的中心再重新聚类；

(5)重复第2～4步，如果聚类中心不再发生变化，就终止算法。

聚类算法完成后，每个簇的中心就是基函数的中心矢量，扩展常数一般有两种计算方法：一是采用统一的偏扩展常数；二是自组织选择法。采用第二种方法，根据各簇中心的距离确定对应径向基函数的扩展常数，其表达式为：

dj=min‖Cj-Ci‖

(3)

其中，dj为第j个簇到其他簇的最小距离；Ci和Cj为两个不同的簇中心。

δj=γdj

(4)

其中，δj为第j个簇的扩展常数；γ为重叠系数。

其次在训练网络中使用梯度下降法来调整隐藏层各神经元的中心矢量、扩展常数，与输出层之间的权值，直到训练结束。

令RBF神经网络学习的目标函数为：

(5)

其中，ei为输入第i个样本时的误差信号，定义为：

(6)

其中，Xi为第i个样本的数据矢量。

为了使目标函数最小化，需要计算每个参数的变化量。

中心点的变化量表达式为：

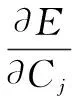
(7)

扩展常数的变化量表达式为：

(8)

权值的变化量表达式为：

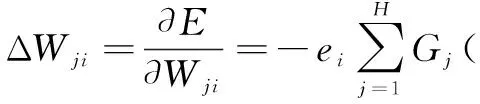
(9)

最后使用LMS算法[11]来调整网络，各参数的修正量应与其负梯度呈正比，其各自的更新表达式如下所述。

中心点的更新表达式为：

(10)

扩展常数的更新表达式为：

(11)

权值的更新表达式为：

(12)

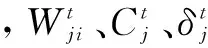
1.3训练神经网络

在进行网络训练前，需要选取训练样本，但也有一定的要求，尽可能选择场景比较相似的样本，相差太大的样本，会影响网络的泛化能力。训练样本为10幅100×100像素的图像。首先对样本进行聚类得到中心矢量以及宽度，然后随机初始化隐藏层到输出层之间的权值。

1.4网络检测

网络训练好之后，可以通过测试来检测网络的泛化能力[13]。使用新的图片对网络进行测试，输入网络经过仿真后输出的图片，就是测试相应的结果。

2 实验结果与分析

为了验证神经网络增强算法的有效性，采用图2作为测试对象，与MSR算法进行结果对比，并从主观和客观两个角度进行评价和分析。

2.1主观评价结果

采用MSR算法和神经网络图像增强算法对图2进行增强处理，结果如图3和图4所示。

图2 实验对象

图3 MSR算法仿真结果

图4 神经网络增强算法仿真结果

从图3和图4的实验结果可以得出：

(1)以人的视觉来观察，经过MSR算法处理后，图像的清晰度得到了一定的改善，但是图像的边缘部分没有体现出来，亮暗分布不均匀，导致损失了一些重要的细节信息，在视觉角度造成了一定的影响，图像质量有待进一步改善。

(2)经过神经网络算法增强之后的图像，边缘和细节较为突出，亮度分布均匀，压缩图像动态范围，对比度均衡，有效地显示了淹没在阴影、光照等区域中的细节，对光照变化的适应能力更强。

2.2客观评价结果

主观结果只是从视觉方面进行评价，因此，采用峰值信噪比(PSNR)、模糊系数K和质量因子Q[14]对增强后的图像进行客观评价，计算方法为：

(13)

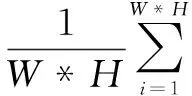
(14)

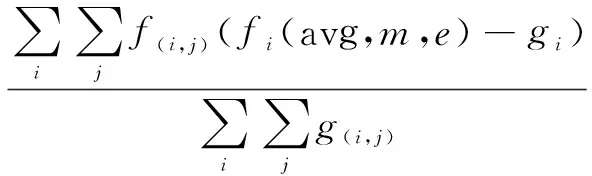
(15)

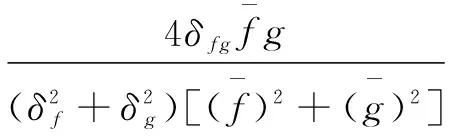
(16)

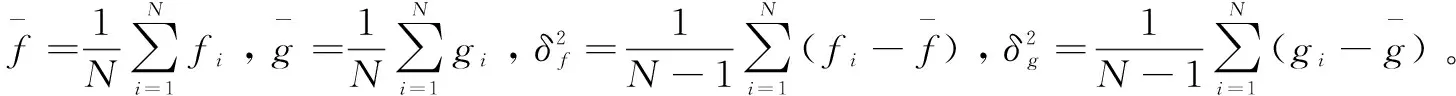
通过上面的公式计算MSR算法和神经网络算法处理之后图像各自对应的值，见表1。

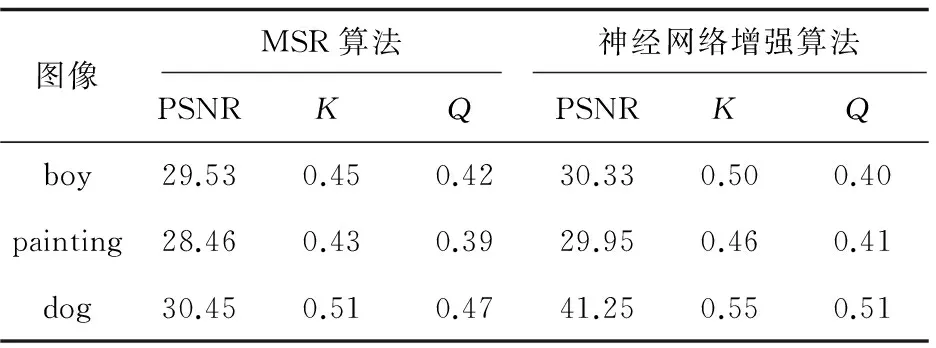
表1 客观指标对比结果

表1中，神经网络算法的PSNR和K都大于MSR算法的PSNR和K的值，这两个值越大，表示增强后的图像质量就越好，因此神经网络图像增强算法在图像细节方面更加丰富，图像清晰度更高，视觉方面更逼真。综合这些指标可知，相对于MSR算法，神经网络算法对图像有较好的增强效果，也具有一定的优越性。

3 结束语

图像增强技术一直是计算机视觉领域中的研究焦点。针对当前的Retinex算法在工作中的局限性，为获得更好的图像增强效率，提出了RBF神经网络的图像增强算法。实验结果表明，相对于Retinex算法，在给定图像评价指标的情况下，RBF神经网络的高反差图像增强方法具有较好的优势。神经网络算法可以保留丰富的细节信息，获得更清晰的图像，实时性强、算法简单灵活，具有广阔的应用前景。

[1] 严 义,吴迎笑.基于神经网络的图像高反差算法的研究与实现[J].仪器仪表学报,2006,27:2302-2305.

[2] Kim Y T.Contrast enhancement using brightness preserving bi-histogram equalization[J].IEEE Transactions on Consumer Electronics,1997,43(1):1-8.

[3] 李学明.基于Retinex理论的图像增强算法[J].计算机应用研究,2005,22(2):235-237.

[4] 王 焱,关南楠,刘海涛.改进的多尺度Retinex井下图像增强算法[J].辽宁工程技术大学学报:自然科学版,2016,35(4):440-443.

[5] 张立明.人工神经网络的模型及其应用[M].上海:复旦大学出版社,1993.

[6] 李明国,郁文贤.神经网络的函数逼近理论[J].国防科技大学学报,1998,20(4):70-76.

[8] Yu B,He X.Training radial basis function networks with differential evolution[C]//IEEE international conference on granular computing.[s.l.]:IEEE,2006:369-372.

[9] 殷 勇,邱 明.一种基于高斯核的RBF神经网络学习算法[J].计算机工程与应用,2002,38(21):118-119.

[10] Krishna K,Murty M N.Genetic K-means algorithm[J].IEEE Transactions on Cybernetics,1999,29(3):433-439.

[11] 刘颖超,张纪元.梯度下降法[J].南京理工大学学报:自然科学版,1993(2):12-16.

[12] 卫 敏,余乐安.具有最优学习率的RBF神经网络及其应用[J].管理科学学报,2012,15(4):50-57.

[13] 李 杰,韩正之.神经网络的学习误差函数及泛化能力[J].控制与决策,2000,15(1):95-97.

[14] 佟雨兵,张其善,祁云平.基于PSNR与SSIM联合的图像质量评价模型[J].中国图象图形学报,2006,11(12):19-24.

Research on High Contrast Image Enhancement Algorithm Based on Neural Network

LIANG Kang-kang，LI Tao

(College of Computer Science,Xi’an University of Posts and Telecommunications,Xi’an 710121,China)

In allusion to the problem of large computational complexity for the multi-scale Retinex algorithm in process of image enhancement，the RBF neural network is proposed as a high contrast image enhancement algorithm,in which the feature vectors of 3×3 neighborhood pixels and the eigenvectors corresponding to the target image is obtained from the training data set and the center vector and the expansion constant of the network hidden layer is determined by the clustering algorithm and thus the optimal solution is acquired by the gradient descent method to make network converge quickly.The RBF neural network has been employed to establish the non-linear mapping relationship between the high contrast image and the enhancement algorithm and the image can be processed quickly,even in real time,according to the network parameters.The experimental results show that it has not only improved the edge and detail of the image but also promoted better sharpness of the image than traditional algorithms based on Retinex theory.Therefore,it is effective,which indicates better perspective in enhancement of high contrast image.

neural network;high contrast;feature vector;quick convergence;image enhancement

2016-10-18

：2017-02-22 < class="emphasis_bold">网络出版时间

时间：2017-07-11

国家自然科学基金重点项目(61136002)

梁康康(1990-)，男，硕士研究生，研究方向为图像处理、机器学习；李 涛，教授，博士，CCF会员，研究方向为计算机体系结构、神经网络、机器学习、图像处理。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170711.1456.062.html

TP391

:A

:1673-629X(2017)09-0097-04

10.3969/j.issn.1673-629X.2017.09.021