基于密度与最小距离的K-means算法初始中心方法

戚后林，顾 磊

(南京邮电大学 计算机学院，江苏 南京 210003)

基于密度与最小距离的K-means算法初始中心方法

戚后林，顾 磊

(南京邮电大学 计算机学院，江苏 南京 210003)

为了克服在传统K-means聚类算法过程中因初始类簇中心的随机性指定所带来的聚类结果波动较大的缺陷，提出了一种基于密度与最小距离作为参数来确定初始类簇中心的算法。该算法根据一定的规则计算数据对象的密度参数，在计算完数据集中每条数据的单点密度之后，计算每个数据对象与较其密度大的其他数据对象的最小距离，以密度和最小距离作为参数，选取密度和最小距离同时较大的点作为K-means聚类过程的初始类簇中心。实验结果表明，在类簇数目确定的情况下，应用该算法确定的初始K-means类簇中心，在标准的UCI数据集上能够进行K-means聚类，且与随机选择类簇中心和其他使用密度作为参数的算法相比，基于改进后的初始中心方法的K-means聚类算法具有较高的准确率和更快的收敛速度。

K-means算法；类簇中心；密度；最小距离；迭代次数

1 概 述

近年来，随着大数据的兴起，如何从中总结出有价值的数据规律是一个重要任务。聚类作为一种数据分析法，在数据挖掘、图像处理等方面都有重要应用。聚类算法包括基于划分的方法、基于层次的方法、基于密度的方法、基于网格的方法和基于模型的方法。聚类分析的目的是数据集合应用不同的策略划分成相似的类簇的过程，从而使同一个类簇具有较高的相似度，而不同的类簇之间尽可能不同。同时聚类分析作为一种数据划分的方法，也可以作为其他数据挖掘方法的一个预处理步骤。

K-means算法[1]是MacQueen提出的一种聚类方法。作为一种典型的基于划分的聚类算法，其特点为：几何意义直观，收敛速度快，资源消耗较少等。但缺点也显而易见：由于算法的初始点通常在算法开始时随机给出，算法的结果很不稳定；同时，算法对于初始类簇中心较为敏感，容易陷入局部最优，类簇中心的数目需要事先给定。

假设在n个数据点中找到k个聚类中心c1,c2,…,ck,使得每个数据xi与其最近的聚类中心cv的平方距离和最小化(该距离和称为偏差Δ)，也即Δ收敛。

输入：类簇的数目k以及n个记录的数据集；

输出：k个类簇，Δ最小或者收敛。

(1)初始化。指定k个类簇中心c1,c2,…,ck。

(2)分配xi。找到距离xi最近的类簇中心cv,并将其分配到其最近的类簇中心cv。

(3)修正cv。通过不断地计算簇的平均值，找到更加合适的聚类中心cv。

(4)计算偏差：

(1)

(5)Δ收敛。如果收敛，返回c1,c2,…,ck，并终止算法，否则返回步骤(2)。

为了克服K-means算法的缺陷，学者们试图从不同角度去改进K-means算法。文献[2]研究了确定K的算法，该算法假设数据集的子集服从高斯分布，然后在K-means聚类过程中不断增加K的大小，直到数据集满足假设，但是对于不服从高斯分布的数据集，该算法仍然存在缺陷。文献[3]通过K-d树来划分数据集，然后利用多个局部区域密度选择初始中心的方法，该算法依赖树节点的数量，当数据集的维度较大时，该算法的运行时间较长。文献[4]提出一种基于平均密度优化初始类簇中心的算法(adk-means)，该算法首先找到数据集中的噪点，在算法执行过程中，噪点不参与聚类过程，但是该算法需要人为指出噪点，当数据集较大时，算法的主观性较强。文献[5]提出一种基于密度的算法，该算法通过缩小维度来加快初始化的过程，不断把可能的类簇中心移向高密度点，直到得到最大的K个最高密度点作为初始的类簇中心，但是该算法的运行迭代次数太高，运行时间较长。文献[6]提出利用二分搜索方法来寻找最佳的K个初始类簇中心。文献[7]提出一种基于密度的网格算法，该算法在Map-Reduce框架中确定K值的大小以及噪点的位置。文献[8]提出了密度峰值进行快速搜索的聚类方法，算法假设类簇中心主要有两个特征，一是具有较高的密度，二是距离比其密度大的类簇中心的最小距离较大。在计算出密度与最小距离决策图时，可以很直观地看到类簇中心和噪点，与文献[4]一样，该算法同样需要人为指出数据集中的噪点，同时，对于截断距离也有很大的主观性。文献[9]提出一种基于最小方差优化初始中心的算法，避免了重复计算数据集到类簇中心的距离，减少了迭代次数，缩短了聚类时间。文献[10]提出一种基于密度与特定阈值的改进K-means算法，该算法首先计算数据集中每个点的密度，然后利用阈值不断迭代较小的密度点加入到类簇中心集合，直到集合中的元素个数到达K为止。文献[11]提出一种基于数据集平均密度与最小距离的聚类算法，该算法计算密度较小的点距离较大点的最小距离，然后将最小距离与平均密度做乘积，由此来计算出离群点，反复迭代，不断剔除离群点，直到剩下K个点来作为初始的类簇中心。文献[12]为了减少K-means算法在数据量较大时运行时间较长的问题，提出在MapReduce平台下运行多路K-means(Mux-Kmeans)算法。文献[13]提出一种基于K-means的聚类算法，该算法包括两个过程:利用K-means算法分割较为稀疏的子数据集，然后利用平均距离对已经分割好的子数据集进行合并。文献[14]提出一种基于密度与最佳距离的K-means初始中心选择方法，该算法利用配置函数的最优值选择初始的类簇中心，同时也可以减小迭代次数。文献[15]为了解决高维数据集聚类，提出了基于K-means算法的K-String算法。

为了解决传统K-means算法在聚类过程中初始中心随机选择的缺陷，在研究基于密度与最小距离的K-means初始中心选择算法原理和步骤分折的基础上，提出了改进的K-means初始中心算法，并进行了验证实验和对比分析。

2 基于密度与最小距离的K-means算法聚类

传统的K-means算法对于初始中心的选取比较敏感，因此，随机性地选取初始中心可能会影响聚类结果的速度和稳定性。而基于密度选取的初始中心则具有主观性，例如，当数据集中两个数据点的密度一样时，如何取舍会直接影响到聚类的结果。提出的算法综合数据集中数据点的密度参数和最小距离参数，引入其他参数作为初始类簇中心的选取指标。

2.1基本定义

设数据集中含有M个样本数据，每个样本有N个属性，则任意数据可以表示为x=(x1,x2,…,xm)。

定义1：数据点x与y之间的距离为欧氏距离d(i,j):

d(i,j)=

(2)

定义2：截断距离dc，定义为整个数据集中点与点之间距离的平均值:

(3)

定义3：样本数据点pi的密度ρi。表示以pi为圆心，dc为半径的圆，包含在圆内其他数据点的数量之和。ρi越大，pi成为初始中心的可能性越大。

(4)

定义4：点pi到其他更高密度点之间的最小距离为δi，代表数据点pi与pj的不相似度，δi越大，说明该点距离其他较大的类簇中心越远，即该点成为类簇中心的可能性较大。

δi=min(d(i,j)),j:ρj>ρi

(5)

对于密度ρi最大的点pi，其最小距离定义为：δi=minj(d(i,j))。

定义5：最终决定样本点pi能否成为类簇中心的决定性参数θi，综合点pi的密度与最小距离，其值直接决定此点是否能成为类簇中心。θi值越大，说明此点在拥有较大密度的同时，距离其他较高的类簇中心也较远，即此点成为初始中心的可能性较大:

θi=ρi×δi

(6)

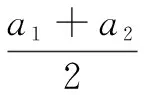
2.2算法描述

在K-means算法中，数据集中点的距离可以使用欧氏距离来衡量，选取数据集的平均距离dc作为截断距离，有利于算法收敛。两点之间的距离越小，说明两点越相似,但是在初始类簇数目一定的情况下，选取一点作为初始的类簇中心关系到聚类结果的准确性和迭代次数。假设类簇中心被其他较低密度的中心所包围，在计算出每个点pi的密度ρi之后，同时计算pi距离较高密度类簇中心的最小距离θi,最后计算出pi点的参数θi。算法的详细描述如下：

(1)根据定义1计算出数据集中任意两点pi与pj的距离d(i,j),并根据定义2计算出数据集最大平均距离作为截断距离dc。

(2)通过定义2及定义3计算出数据集中每个点的密度ρi及距较高密度类簇中心的最小距离δi。对于密度最大的点，δi定义为其他点到此点的最大距离。

(3)根据定义5计算出θi。

(4)选取K个具有较大θi的点作为K-means算法的初始类簇中心。

(5)利用K-means算法进行聚类。

如图1所示，假设数据集最终被划分为两个类簇。截断距离dc由数据集的平均距离确定后，以任意一点pi为中心，dc为半径的圆所包含其他数据点的个数为pi点的密度ρi。图中，密度较大的三点p1,p2,p3的密度分别为ρ1=4,ρ2=5,ρ3=6。在计算出每个点的密度后，可以看出p1距离密度较大的点为p2,p3，但是与p2的距离最小。密度较p2较大的点只有p3，由于p3是整个数据集中密度最大的点，所以在计算p3点的最小距离时，只需在数据集中计算距离p3最远的点。计算出p1,p2,p3距离其他较高密度点的最小距离分别为δ1,δ2,δ3。选取θi=ρi×δi较大者作为初始类簇中心，在图1的二维数据集中，假设要选取两个类簇中心，由于p2,p3的θi较大，故选取p2,p3为初始的类簇中心。

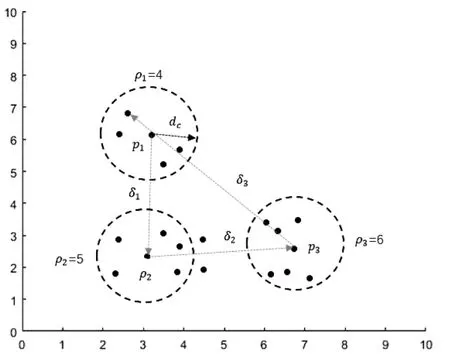
图1 二维数据的密度和最小距离表示

3 实 验

3.1数据集描述

为了验证上述算法选取初始类簇中心的有效性，选取了专用于测试聚类算法性能的UCI数据集。UCI是一个专门用于测试机器学习与数据挖掘算法的数据库，库中的每个数据集都有明确的分类，因此可以直观表示聚类结果的质量。对Iris,Wines,Seeds,Banlance-scale四个数据集进行了测试，按照准确率、迭代次数来评价算法的性能。表1简单介绍了实验所用数据集的情况。

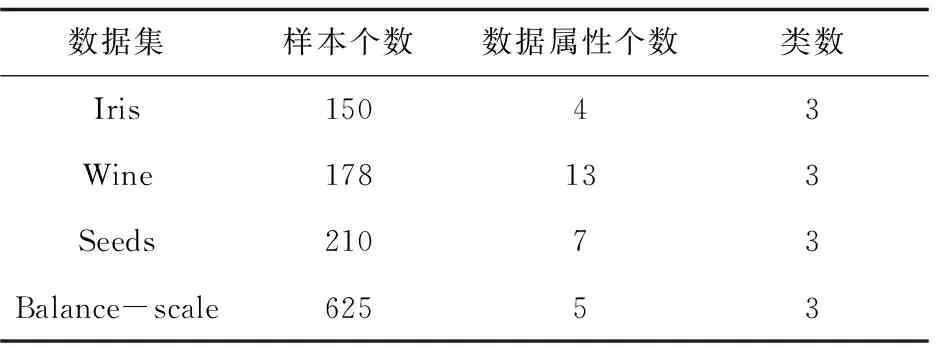
表1 UCI数据集描述

3.2实验结果及分析

用到的K-means初始中心选取算法不仅计算数据集中每个数据点的密度值ρi，还将计算距离密度较高的点的最小距离δi，然后将其与密度做乘积得到θi。在四个数据集上随机选取10个点作为初始的类簇中心，对提出算法与其他初始中心选取算法进行了实验。表2为在Iris与Wine数据集上的实验结果，表3为在Seeds与Balance-scale数据集上的实验结果。

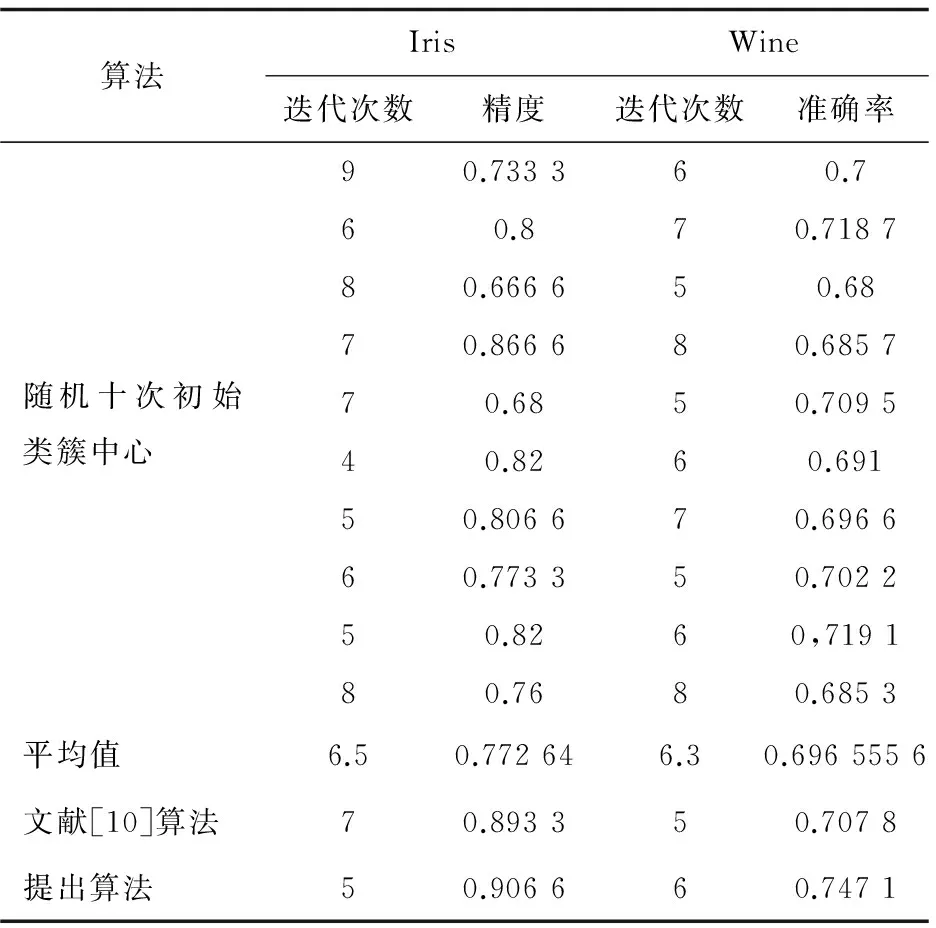
表2 Iris与Wine数据集的实验结果

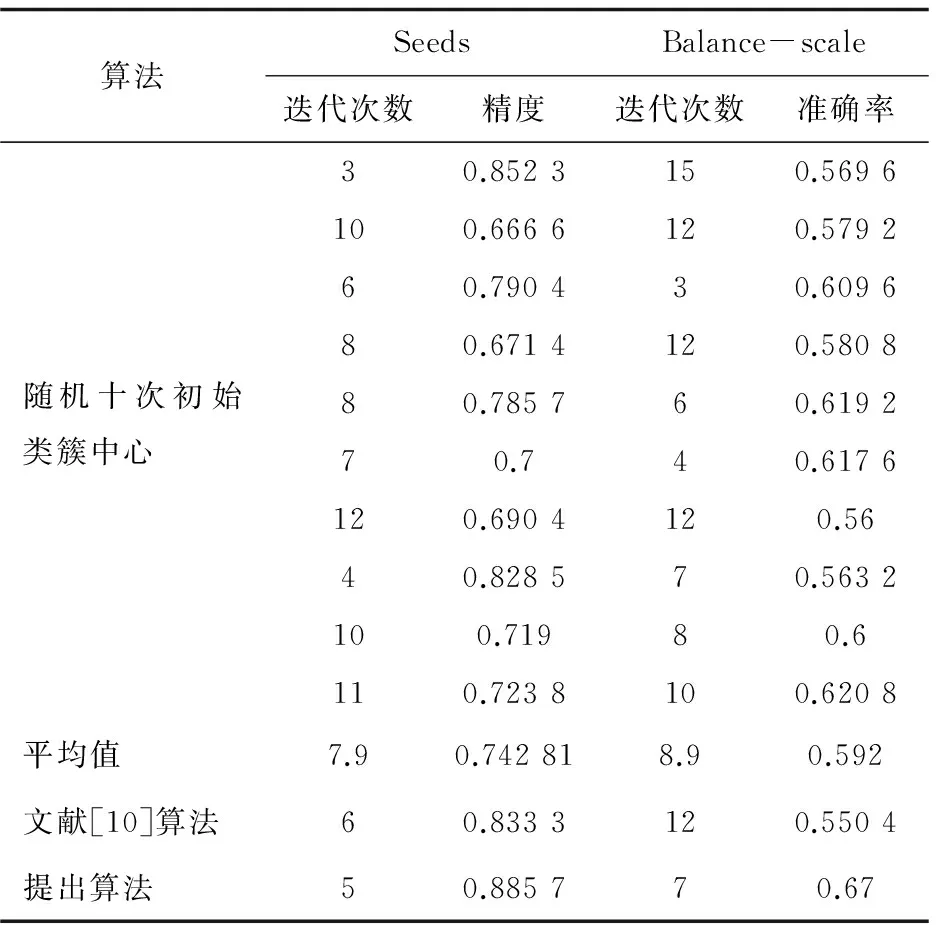
表3 Seeds与Balance-scale数据集的实验结果

为了验证提出算法较其他初始中心选取算法具有较好的性能，分别选取了传统的初始中心算法与文献[10]算法进行对比。

在实验过程中发现，三种算法的类簇划分个数相同，但实验结果却不同。传统的随机化初始中心算法无论是准确率还是迭代次数都不稳定，无法计算出θi较大者作为初始的类簇中心。

Iris数据集中，传统初始中心选择算法的准确率和迭代次数都波动较大，十次实验的平均准确率为0.772 6，平均迭代次数为6.5，文献[10]算法选择的初始中心准确率为0.893 3,在迭代7次后算法收敛。在利用提出算法选取的类簇中心实验中，θi较大的三个点为(50,16,123),对应的θi值为(950,930,1 276)，算法的迭代次数为5，准确率为0.906 6。

Wine数据集中，传统初始中心选择算法的准确率为0.696 5，平均迭代次数为6.3，而文献[10]算法选择初始中心的准确率为0.707 8，迭代次数为5。利用提出算法计算出的θi较大的点为(132,32,78),对应的θi值为(8 320,10 952,12 300)，算法的准确率为0.747 1，迭代次数为6。

Seeds数据集中，传统初始中心算法得到的平均准确率为0.742 8，平均迭代次数为7.9，文献[10]算法的平均准确率为0.833 3，迭代次数为6。而在提出的初始中心选取算法中，计算出θi较大的点为(22,184,53)，对应的θi值分别为(693,396,440)。在选取了相应类簇中心后，利用K-means算法得到的聚类结果准确率为0.885 7，迭代次数为5。

Balance-scale数据集是维度较大的数据集，传统初始中心选择算法的平均准确率为0.592，平均迭代次数为8.9，文献[10]算法得到的准确率为0.550 4，迭代次数为12。利用提出算法得到θi较大的三个点为(122,262,476),对应的θi值为(680,710,578),算法在迭代7次后收敛，聚类准确率为0.67，可见初始中心选择算法对高维数据同样也有较高的准确率与迭代速度。

4 结束语

在分析传统的K-means初始中心选取算法和改进初始中心选取算法不足的基础上，提出了一种基于密度与最小距离优化的初始中心选择算法。该算法根据数据集中每个数据对象的密度与最小距离来确定数据集中类簇的位置。实验结果表明，该算法在消除K-means算法对于初始中心依赖性的同时，减小了迭代次数，提高了运行效率。

[1] MacQueen J.Some methods for classification and analysis of multivariate observations[C]//Proceedings of the fifth Berkeley symposium on mathematical statistics and probability.[s.l.]:[s.n.],1967:281-297.

[2] Hamerly G,Elkan C.Learning the K in K-Means[C]//Advances in neural information processing systems.[s.l.]:[s.n.],2004.

[3] Zhang Xuanyi,Shen Qiang,Gao Haiyang,et al.A density-based method for initializing the k-means clustering algorithm[C]//International conference on network and computational intelligence.[s.l.]:[s.n.],2012:46-53.

[4] 邢长征,谷 浩.基于平均密度优化初始聚类中心的k-means算法[J].计算机工程与应用,2014,50(20):135-138.

[5] Qiao J,Lu Y.A new algorithm for choosing initial cluster cen-ters for k-means[C]//Proceedings of the 2nd international conference on computer science and electronics engineering.Paris,France:Atlantis Press,2013:527-530.

[6] Kumar Y,Sahoo G.A new initialization method to originate initial cluster centers for K-Means algorithm[J].International Journal of Advanced Science and Technology,2014,62:43-54.

[7] Ma L, Gu L, Li B,et al.An improved k-means algorithm based on MapReduce and grid[J].International Journal of Grid and Distributed Computing,2015,8(1):189-200.

[8] Rodriguez A,Laio A.Clustering by fast search and find of density peaks[J].Science,2014,344(6191):1492-1496.

[9] 张晓倩,曲福恒,杨 勇,等.一种高效的基于初始聚类中心优化的K-means算法[J].长春理工大学学报:自然科学版,2015(4):154-158.

[10] 何佳知,谢颖华.基于密度的优化初始聚类中心K-means算法研究[J].微型机与应用,2015,34(19):17-19.

[11] Yuan Q,Shi H,Zhou X.An optimized initialization center K-means clustering algorithm based on density[C]//IEEE international conference on cyber technology in automation,control,and intelligent systems.[s.l.]:IEEE,2015:790-794.

[12] Li C,Zhang Y,Jiao M,et al.Mux-Kmeans:multiplex kmeans for clustering large-scale data set[C]//Proceedings of the 5th ACM workshop on scientific cloud computing.[s.l.]:ACM,2014:25-32.

[13] Lin Y,Luo T,Yao S,et al.An improved clustering method based on k-means[C]//9th international conference on fuzzy systems and knowledge discovery.[s.l.]:IEEE,2012:734-737.

[14] Chu S Y,Deng Y N,Tu L L.K-means algorithm based on fitting function[C]//International conference on applied science and engineering innovation.[s.l.]:[s.n.],2015:1940-1945.

[15] Le V H,Kim S R.K-strings algorithm,a new approach based on Kmeans[C]//Proceedings of the 2015 conference on research in adaptive and convergent systems.[s.l.]:ACM,2015:15-20.

An Initial Center Algorithm ofK-means Based on Density and Minimum Distance

QI Hou-lin，GU Lei

(College of Computer,Nanjing University of Posts and Telecommunication,Nanjing 210003,China)

In order to overcome a large fluctuation caused by the traditionalK-means algorithm clustering with assignment of the random initial cluster centers,an algorithm taken the density and minimum distance as the parameters to determine the initial cluster centers is proposed,which calculates the density parameter of the data object according to certain rules and minimum distance between each data object and other data objects after having calculated single point density of each data in the data set.The larger one among the densities and minimum distances has been chosen as initial cluster center in the process ofK-means clustering.Experimental results show that it has higher accuracy and faster convergence rate compared with ones using randomly selected cluster centers and using density as a parameter forK-means clustering on standard UCI data set.

K-means algorithm;cluster center;density;minimum distance;iteration number

2016-09-07

：2016-12-22 < class="emphasis_bold">网络出版时间

时间：2017-07-11

国家自然科学基金资助项目(61302157)

戚后林(1990-)，男，硕士研究生，研究方向为中文文本分类；顾 磊，副教授，硕士生导师，研究方向为中文信息处理、机器学习。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170711.1454.028.html

TP301.6

:A

:1673-629X(2017)09-0060-04

10.3969/j.issn.1673-629X.2017.09.013