基于MapReduce的单遍K-means聚类算法

唐 浩，杨余旺，辛智斌

(1.南京理工大学 计算机科学与工程学院，江苏 南京 210094；2.淮海集团工业有限公司，山西 长治 046000)

基于MapReduce的单遍K-means聚类算法

唐 浩1，杨余旺1，辛智斌2

(1.南京理工大学 计算机科学与工程学院，江苏 南京 210094；2.淮海集团工业有限公司，山西 长治 046000)

K-means应用于MapReduce框架的大数据处理可显著提高K-means对大数据集的处理能力。但K-means聚类算法需要进行多次迭代才能达到可接受的效果，并将每次迭代作为一个独立map作业执行，需要读写整个数据集，从而导致显著的I/O消耗，与MapReduce框架的设计理念不符。为此，提出了一个基于MapReduce的单遍K-means算法(MRSK)。该算法采用流数据单遍算法读取数据，聚类时采用K-means++初始化seeding算法得到初始聚类中心。在理论分析MRSK算法复杂度的基础上，进行了MRSK算法的测试验证和相关分析。验证实验结果表明，相对于基于MapReduce和基于数据流的K-means聚类算法，所提出的MRSK算法在执行速度和聚类效果方面具有更好的优势。

MapReduce框架；数据聚类；K-means++；Mahout；单遍技术

0 引 言

K-means[1]聚类算法是数据挖掘领域中的一种重要方法，由于计算简单、收敛速度快，在机器学习、图像处理等领域应用广泛。近年来，随着数据量的不断攀升，传统的K-means聚类分析方法已无法满足大数据[2]的需求，所以亟需对传统的K-means方法做出改进以支持大规模数据分析。

MapReduce[3]是由谷歌提出的一种大数据并行计算框架。MapReduce的3个主要特点：模型使用方便、适用于大型数据处理、可扩展并内置容错，使其成为一种理想的大数据处理框架[4]。如今，K-means已经成功地应用在了MapReduce框架中。

Zhao W等提出的基于MapReduce的K-means聚类算法，是一种快速聚类方案，利用了运行在Hadoop[5]框架上的Mahout[6]项目，称之为PKMeans[7]。艾隆等提出的基于数据流的K-means算法，利用了基于数据流的单通技术[8]，称之为SKMA[9]。

上述解决方案为了达到可接受的结果，都需要对整个数据集进行多次迭代，而MapReduce本质上不支持迭代。在每次迭代中，整个数据集必须从磁盘加载到内存中，数据集经过处理后，输出时必须再一次写入磁盘，因此，每一次迭代都会产生大量和I/O相关的操作，如磁盘I/O、数据序列化等等，严重影响了程序的执行速度。所以这些方案并不适合MapReduce框架。Hadian和Shahrivari为了共享内存，实现并行计算，提出了一种并行的单遍聚类算法[10]，但是该算法没有使用MapReduce框架。

为此，文中提出一种基于MapReduce的单遍K-means聚类算法(MRSK)。该算法利用流数据单遍算法读取数据，在数据聚类过程的map阶段采用K-means++初始化Seeding算法[11]得到中间簇中心集；在reduce阶段，采用支持权重的K-means++初始化Seeding改进算法进行中间簇中心集处理，并获得初始聚类中心，再利用K-means进行聚类计算，得到最终聚类结果。

1 K-means++与单遍算法

1.1K-means++初始化Seeding

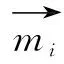
K-means是一种简单快速且高效的聚类算法[12]。质心的计算如下：

(1)

初始聚类中心的选取对K-means影响很大，但是K-means随机选取初始聚类中心，无法保证聚类效果。K-means++通过初始化Seeding算法[13]，可以提供一个较好的初始聚类中心。

通过式(2)初始聚类中心：

(2)

初始化Seeding算法的步骤为：

算法1：K-means++中心初始化。

1:执行K-means++(M,k)；

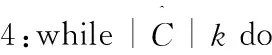
5:end while

7:结束

1.2单遍算法

单遍算法[14]是流式数据聚类的经典方法。该算法依据数据输入顺序依次处理数据，依据当前数据与现有类的匹配度大小，判定该数据归入已有类或另外创建一个新类。

利用欧氏距离作为匹配度判定依据，欧式距离公式如下：

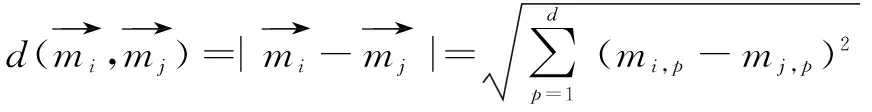
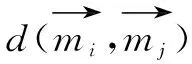
2 MRSK算法

2.1算法流程

提出MRSK方法，是为了解决现有基于MapReduce方案中因多次迭代而引起的I/O消耗问题。在MRSK方法中，将整个数据集分割成更小的，可存于每台机器内存的数据块，并分发这些数据块到可用的机器。然后，每个块由所处的机器独立聚簇，每个块经过并行处理后产生若干中间簇中心，之后将中间簇中心的集合从每台机器中抽取出来作为一个更小的数据集装载进单独一台机器的主存中，最终的聚类中心从中间簇中心集中通过重新聚类产生。

每个块所在的机器在处理数据时采用单遍法，对当前到达的数据进行聚类，依据匹配度大小，将数据判为已有类或创建一个新类。采用单遍算法，计算过程中整个数据集只被读取了一次。

由于每个块的处理是相互独立的，每个块可以在一个专用的map任务中处理。也就是说，每个map任务选择一个数据集分块，并在数据块上执行K-means++初始化Seeding算法，得到中间簇中心和每个簇中心的权重，然后各聚类中心和各中心的权重作为结果输出。Map过程完成后，所有加权中心形成中间簇中心集，并作为map输出。这个中间簇中心集会分配给一个单独的reduce任务。Reduce任务得到中间簇中心和它们的权重后，会采用改进的支持权重的K-means++初始化Seeding算法得到初始簇中心，然后通过改进的K-means算法得到最终的聚类中心。MRSK算法的完整流程如算法2所示。

算法2:MRSK算法。

1：执行MRSK(M,k)

2：Map过程：

3：将数据集M分割为∂块，构成集合M=M1,M2,…,M∂；

4：对于集合M中的每个Mi执行步骤5；

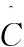
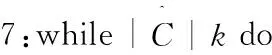
8：end while

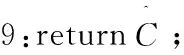
10：Map任务结束；

11：Reduce任务：

12：Map任务的输出构成中间簇中心集Cw；

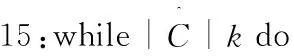
16：end while

20：结束

2.2MRSK聚类

把整个执行过程放在MapReduce框架中。数据块处理放在map阶段，中间簇中心集的处理放在reduce阶段。如前所述，提出方案的主要优势是使用了数据流单遍算法，降低了迭代过程中的I/O消耗，同时也提高了执行速度。

在这两个阶段中，均使用了K-means++算法，这是因为K-means++的初始化Seeding算法有助于提高算法的聚类效果。对于每个数据块，利用K-means++算法取得在此数据块上的k个聚类中心。因此，如果有c个数据块，在每个数据块上使用K-means++后，将会生成一个拥有k·c个元素的中间簇中心集合。这个集合就是map阶段的输出。

此外，使用聚类中心的权重来帮助提高MRSK的精确度。每个聚类中心分配的数据项的个数表明了该中心的重要性。因此，对于获得中间簇中心，必须拓展K-means++算法以支持加权。为了达到此目的，需要改进初始化聚类中心计算方法(式2)和聚类中心计算方法(式1)。

在K-means++算法中，利用式(4)初始化聚类中心，在之后的迭代过程中，使用式(5)计算簇中心。

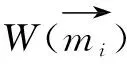
(4)

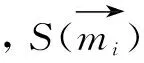
初始化簇中心利用式(5)：

(5)

之后的迭代过程中，簇中心的选取使用式(6)：

(6)

3 算法复杂度分析

典型的聚类算法有三种类型的复杂度：时间复杂度、I/O复杂度和空间复杂度。MRSK有两个过程：map阶段处理数据块和reduce阶段在中间簇中心集上运行K-means++算法。为确定每一种类型的复杂度，必须考虑这两个阶段。对于MRSK复杂性的分析，提出了以下假设：k为簇的个数，n为数据集中数据项的数量，c为每个数据块的大小，p为可以并行处理的数据块数，I为直到收敛为止总的迭代次数。值得注意的是，假设计算和存储一个数据项的时间复杂度为O(1)(在大部分相似的文献中也都做了这样的假设)。3.1数据块大小设定

为了实现聚类，MRSK需要两个重要的参数：聚簇个数k和数据块大小c。如何设置块大小需要考虑，理论上，块大小最小为k，最大为n，但这两个极端值都并不切合实际。

但是如果数据集不是非常大，块大小可以被设置为较小的值，如k·logn或者k的倍数。因为块较小，可以产生更多的中间簇中心，从而可以更好地代表原始数据集，得到的聚类结果也会更好。

3.2I/O复杂度

3.3空间复杂度

3.4时间复杂度

3.5与相关工作进行复杂度对比

在前面提到的PKMeans和SKMA中，PKMeans利用了Apache Hadoop Mahout项目，是标准K-means在MapReduce框架中的实现；SKMA算法将原始数据集分割为多个小的子集，在每个子集上利用K-means#算法选择k个中心构成中间簇中心集，然后利用K-means++算法[11]从中间簇中心集中选出最终的k个中心。

表1分别列出了PKMeans、SKMA和MRSK的三种复杂度。在大数据集中，数据量n很大，所以聚类算法要达到收敛，需要经过多次迭代，从而导致I很大，而且容易得到n≫I>k>p。可以发现，在I/O复杂度上，PKMeans最高，MRSK与SKMA相当；但是在时间复杂度和空间复杂度上MRSK均比其他两种算法低。通过比较可以得出，相对于另外两种算法，MRSK复杂度最低。

表1 复杂度比较

4 实验与结果分析

4.1实验设置

实验中，使用6台服务器搭建Hadoop集群，每台机器CPU为Intel Xeon E5520*2，内存16 G。机器上安装Centos6.5(64位)系统，Open JDK 7，CDH5(Cloudera Hadoop 5)和Mahout0.8。

主要目标是比较MRSK算法和另外两种算法的执行速度和精确度。为了比较三种算法对于大数据集的处理能力和效果，生成了四个大型合成数据集，分别包括10，50，100，和500个簇。每个数据集拥有10亿数据项。每个数据项有5个特征，标准偏差为10，因此，最优聚类时，SSE大约为5·1011。

4.2评价指标

在实验中，主要比较在相同情况下三种算法的执行速度和聚类效果。执行速度通过执行时间来比较。聚类效果通过误差平方和函数SSE(Sum of Squares for Error)来比较。SSE显示簇的紧凑性，SSE值低，意味着聚类效果更好。SSE计算公式如下：

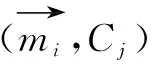
(7)

4.3实验结果分析

标准K-means和SKMA算法，利用Apache Mahout项目中基于MapReduce框架的版本。图1为k增加时PKMeans、SKMA和MRSK的执行时间变化图。图2为k增加时三种算法的SEE变化图。

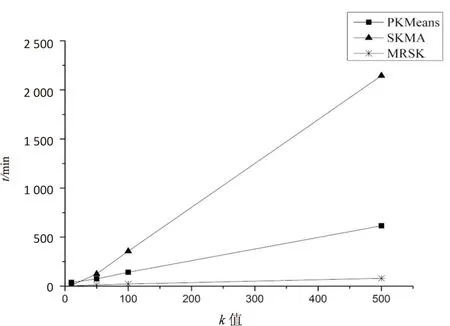
图1 k和时间的关系

从图1的结果可以看出，相对于其他方案，MRSK的速度更快。尤其是k大于100时，MRSK的速度远快于另外两种算法。在图2中，MRSK的聚类效果也比另外两种算法要好，随着k值增大，SSE越来越接近5·1011，而5·1011正是预估的理论值。图中，PKMeans的聚类效果一直比另外两种算法差。k=10时，SKMA和MRSK的SSE值大小相当，k大于10时，MRSK的SSE值逐渐低于SKMA。而且，随着簇的增加，MRSK一直保持着较低的SSE值。

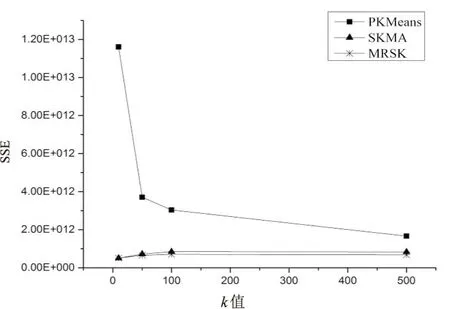
图2 k和SSE的关系

实验结果表明，MRSK在保证聚类效果的前提下，降低了I/O开销，提高了执行速度。

5 结束语

针对K-means的迭代性质并不能在MapReduce框架中被模型化，需要反复读写磁盘导致极高I/O开销的问题，提出了基于MapReduce的单遍K-means算法。理论分析和实验结果均表明，MRSK有效提高了算法执行速度，降低了I/O开销，为处理大数据集上的大量聚簇问题提供了一个有益的解决思路和方案。下一步的研究重点是利用包括k-d树在内的临近搜索方法，进一步降低算法的时间复杂度。

[1] Wang L,Tao J, Ranjan R,et al. G-Hadoop:MapReduce across distributed data centers for data-intensive computing[J].Future Generation Computer Systems,2013,29(3):739-750.

[2] 王 珊,王会举,覃雄派,等.架构大数据:挑战、现状与展望[J].计算机学报,2011,34(10):1741-1752.

[3] Dean J,Ghemawat S.MapReduce:simplified data processing on large clusters[C]//Conference on symposium on operating systems design & implementation.[s.l.]:USENIX Association,2004:107-113.

[4] Dean J,Ghemawat S.MapReduce:a flexible data processing tool[J].Communications of the ACM,2010,53(1):72-77.

[5] White T.Hadoop:the definitive guide[M].[s.l.]:[s.n.],2010.

[6] Thangavel S K,Thampi N S,Johnpaul C I.Performance analysis of various recommendation algorithm using apache Hadoop and mahout[J].International Journal of Scientific & Engineering Research,2013,4(12):279-287.

[7] Zhao W,Ma H,He Q.Parallel k-means clustering based on MapReduce[C]//IEEE international conference on cloud computing.[s.l.]:IEEE,2009:674-679.

[8] 谢国富,王文成.单遍数据读取的GPU上的多片元效果绘制[J].计算机学报,2011,34(3):473-481.

[9] Ailon N,Jaiswal R,Monteleoni C.Streaming k-means approximation[C]//Conference on neural information processing systems.Vancouver,British Columbia,Canada:[s.n.],2009:10-18.

[10] Hadian A,Shahrivari S.High performance parallel k-means clustering for disk-resident datasets on multi-core CPUs[J].Journal of Supercomputing,2014,69(2):845-863.

[11] Arthur D,Vassilvitskii S.k-means++:the advantages of careful seeding[C]//Proceedings of the eighteenth annual ACM-SIAM symposium on discrete algorithms.[s.l.]:Society for Industrial and Applied Mathematics,2007:1027-1035.

[12] Hartigan J A,Wong M A.A K-means clustering algorithm[J].Applied Statistics,2013,28(1):100-108.

[13] Bahmani B,Moseley B,Vattani A,et al.Scalable k-means++[J].Proceedings of the VLDB Endowment,2012,5(7):622-633.

[14] 张培伟.基于改进Single-Pass算法的热点话题发现系统的设计与实现[D].武汉:华中师范大学,2015.

A Single-passK-means Clustering Algorithm with MapReduce

TANG Hao1,YANG Yu-wang1,XIN Zhi-bin2

(1.School of Computer Science and Technology,Nanjing University of Science and Technology,Nanjing 210094,China；2.Huaihai Industrial Group Co.,Ltd.,Changzhi 046000,China)

The application of fittingK-means into MapReduce framework can greatly improve the processing ofK-means on large datasets.ButK-means achieves an acceptable clustering effect through multiple iterations.Each iteration is executed as an independent map job,in which the whole dataset must be read and wrote to slow disks,resulting in high I/O overhead,and it is not consistent with the design concept of the MapReduce framework.Therefore,a single-passK-means clustering algorithm based on MapReduce,called MRSK,is proposed.It reads the data by single-pass and uses theK-means++ seeding algorithm to get the initial cluster center.On the basis of theoretically analyzing the complexity of the MRSK,a series of test and analysis for MRSK is conducted.The experimental results show that compared with the available MapReduce-based and stream-basedK-means variants,MRSK performs both faster execution times and higher quality of clustering results.

MapReduce framework;data clustering;K-means++;Mahout;single-pass

2016-11-04

：2017-03-09 < class="emphasis_bold">网络出版时间

时间：2017-07-11

国家自然科学基金资助项目(61640020)；江苏省科技支撑计划(BE2012386，BE2011342)；江苏省农业自主创新项目(CX(13)3054，CX(16)1006)；江苏省重点研发计划(BE2016368-1)；深圳市战略性新兴产业发展专项资金项目(JCYJ20130331151710105)

唐 浩(1990-)，男，硕士生，研究方向为云计算和大数据处理；杨余旺，教授，研究方向为云计算和大数据处理、网络编码、传感器网络。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170711.1457.086.html

TP301.6

:A

:1673-629X(2017)09-0026-05

10.3969/j.issn.1673-629X.2017.09.006