范数度量下的三项递归式数值稳定性判据

付 波，胡 什，赵熙临，徐光辉

范数度量下的三项递归式数值稳定性判据

付 波，胡 什，赵熙临，徐光辉

（湖北工业大学电气与电子工程学院，湖北武汉430068）

正交矩的数值稳定性分析是近年来图像处理中研究的热点。研究对象是正交矩解析式中最为常用的三项递归公式，介绍正交矩的三项递归公式及数值稳定性的概念；然后以欧几里得范数作为恒量其稳定性的标准提出一种基于其计算系数极限存在与否判断其数值稳定性的判据，并给予详尽证明；最后运用两个实例证明此判据的可行性。

正交矩三项递归式；欧几里得范数；计算系数极限；数值稳定性

作为正交矩计算基础的三项递归公式在进行高阶计算时存在数值不稳定的问题。R.Mukundan在研究Tchebichef矩时提出了随着正交矩分析的图像越来越大，高阶矩的计算过程中各种误差会造成矩数值计算不稳定［1］，最终导致图像重构时模糊。G.R.Amayeh等［2］试图采用提高正交矩计算精度的方法来抑制其传递误差，但仅仅只是对其作出了抑制，无法从根源上解决问题。郭［3］指出其误差根源在于计算机系统本身产生的截断误差和舍入误差，所提出的一种将三项递归式转化为离散状态方程来研究其稳定性的方法，是目前较令人信服的方法，然而其随后提出来的利用李亚普洛夫方法解决系统稳定性的方法适用范围过窄，只能判断Legendre矩以及Tchebichef矩等少量矩的稳定性。

笔者在总结上述学者工作的同时，也对常见的几种正交矩三项递归式进行了细致的研究，得出了一个规律：系数极限存在的正交矩基函数一般具有数值稳定性，而系数极限为无穷的正交矩基函数则不具有数值稳定性。立足于上述规律，笔者提出了判断正交矩三项递归公式稳定性的一个充分条件和判断其不稳定性的一个充分条件，并从欧几里得范数和距离空间的角度对其进行了严谨的证明。最后利用此判据分别验证了极限存在的Legendre矩的数值稳定性以及极限为无穷的Tchebichef矩的不稳定性，证明了其可行性。

1 正交矩三项递归公式

在正交矩的解析方法中，利用三项递归公式进行解析是最常使用的方法：

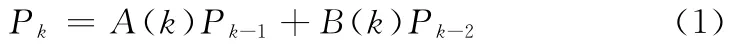
若需要计算较高阶数上述公式的数值，则需要计算机等手段的帮助。然而在计算机的计算过程中，系统本身产生的计算误差会使观测值异于实际值。上述计算误差有可能会在计算过程中被放大，最终影响计算所得的终值。因此分析计算误差的传递过程和三项递归算法的数值稳定性势在必行。在这里采用郭［3］的做法将其化为状态方程来进行研究，设三相递归公式的观测值为Pk，其真实值为P＊k，计算误差为ek，起始二项为P0和P1，P0和P1的误差为e0和e1，可以将式（1）变为：

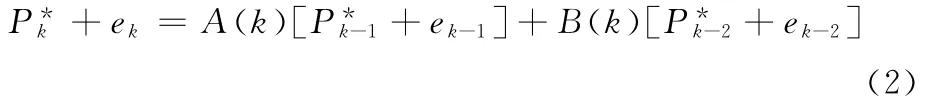
易得，计算真值满足：

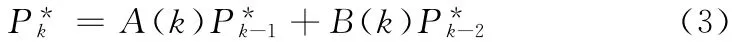
将上式化为矩阵形式，即：

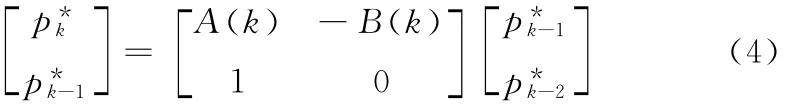
计算误差满足：

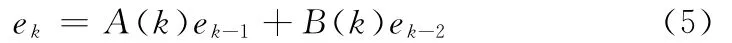
将上式化为矩阵形式，即：

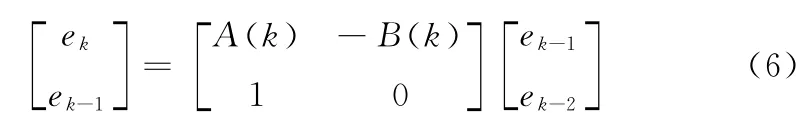
在实际计算过程中，三项递归算法的数值稳定性涉及两个方面：1）真值计算系统（即式（4））本身的稳定性；2）观测误差系统（即式（6））的稳定性。当且仅当式（4）和式（6）所代表的系统均收敛，即代表观测值的系统与代表递归误差的系统均收敛时，整个三项算法才具有数值稳定性。而上述两个系统的传递函数均为：，是一类系统，因此只需研究上述任一系统的稳定性即可。由此将算法数值稳定性本质转化为研究基于式（6）的二阶系统的稳定性。若式（6）所代表的系统是稳定的，则说明递归误差不会在计算中被逐步放大，仍然是可以抑制的，它代表的递归算法具有数值稳定性；反之则是发散的，其递归算法不具有数值稳定性。因此只需判断系统（6）的稳定性即可判断递归算法的数值稳定性。

正交矩三项递归公式的计算系数A与B会随阶数的增加而变化，故其形成的系统（6）为离散线性时变系统，该类系统的稳定性较难判断，目前学术界仍无一定论。在这里文献［4］的方法是利用较为常见的李雅普洛夫第二法［4］来判断，然而值得注意的是：李亚普洛夫定义下的稳定性与三相递归式的数值稳定性还是有细微区别的，无法一概而论；且李雅普洛夫方法过于复杂，对于每一个不同的正交矩多项式需寻求不同的李雅普洛夫函数来进行对应，大大增加了判断的难度。笔者在下节中的研究将回归误差传递的本质，直接从系统（6）的传递函数矩阵入手，以欧几里得范数作为恒量其三项递归式数值稳定性的标准，提出两个较为简洁的稳定性判据，并佐以详细的证明。

2 范数度量下数值稳定性判据

判据1：正交矩三项递归公式（1）数值稳定的充分条件是：其计算系数A或B极限都存在且不为无穷。

判据2：正交矩三项递归公式（1）数值不稳定的充分条件是：其计算系数A或B至少有一者极限为无穷。

证明：由上文分析得，三项递归公式（1）的数值稳定性大致等价于二阶系统（6）的稳定性，系统（6）的传递函数矩阵为：

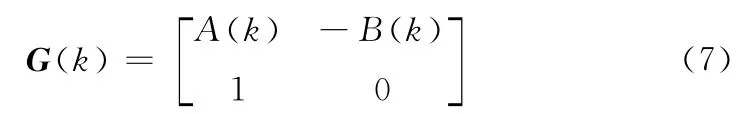
设M2×2（C）是数域C上的方阵，按照通常矩阵的加法与数乘构成的2×2维线性空间［5］，对于幂级数常项矩阵G（k）＝（a（k）ij）2×2∈M2×2（C），定义以下范数：

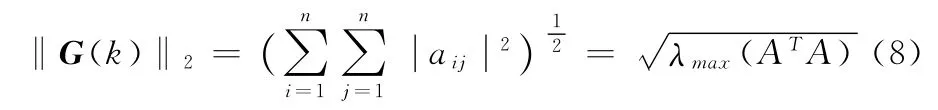
则（Mn×n（C），‖.‖2）是赋范线性空间。在此赋范线性空间下G（k）的范数为：

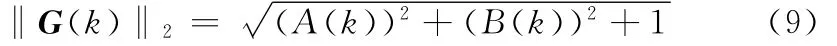
当计算系数A（k）与B（k）均极限都存在且不为无穷时，上述范数G（k）的极限‖G（k）‖存在且不为无穷。这表明代表的递归误差不会在进行高阶计算时放大，即使在计算至无穷阶时误差仍然是有界的，根据上文的推论可以判断此种计算系数下的三项递归公式具有数值稳定性，判据1充分性得证。

当计算系数A（k）与B（k）至少有一为无穷时，上述范数的极限‖G（k）‖为无穷，此时其代表的递归误差会在进行高阶计算时被无限放大，最终会使计算值大幅度偏离真值。由上文的讨论可知：此种计算系数下的三项递归公式不具有数值稳定性，判据2充分性得证。

3 实例验证

本章将利用上文的判据分别对Legendre矩三项递归公式和Krawtchouk矩三项递归公式进行数值稳定性判断。

3.1 Legendre矩三项递归公式

Legendre矩三项递归公式为：得到其计算系数为：

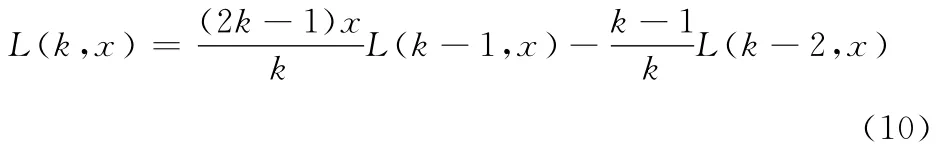
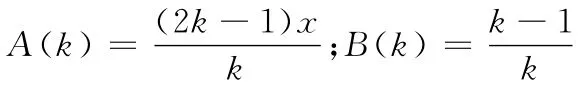
取L（0）＝1，L（1）＝0.5；x∈［－1，1］，在c＋＋大数库中计算0至400阶的Legendre矩三项递归公式的误差。图1代表计算误差随计算阶数的增加的变化情况，其中图1a代表绝对误差的变化，图1b代表相对误差的变化情况，单位用Arbitrary Precision Arithmetic［6，7］对数形式表示。由图1可知：在0至400阶的计算过程中其绝对误差L（k）逐渐趋于稳定，相对误差E（k）除了在150阶和220阶左右较大之外其余均小于e－12，说明整个传递误差的递归过程是收敛［8］的，Legendre矩三项递归公式具有数值稳定性，这与笔者利用判据1得出来的结论一致，说明了判据1的有效性。

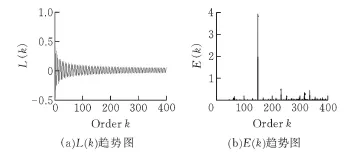
图1 Legendre多项式迭代计算误差随阶数k变化图

3.2 Krawtchouk三项递归公式

Krawtchouk矩三项递归公式为：

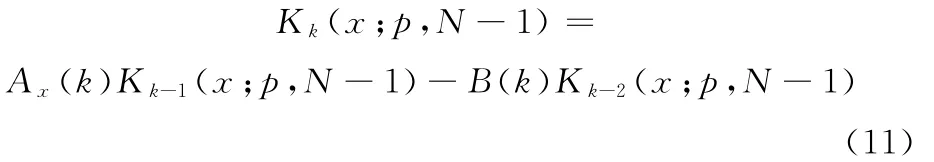
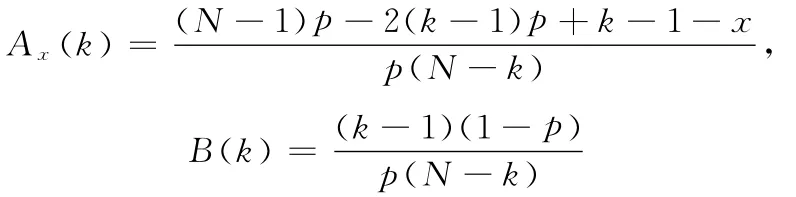
其计算系数为：此时，由于系数N，p的数值不确定性，求得：由判据2可知：Krawtchouk矩三项递归公式在相对意义上不具有数值稳定性。

与Legendre矩不同的是，Krawtchouk多项式计算系数中含有变量参数p。因此取x＝398时，p＝0.1，p＝0.3，p＝0.5，p＝0.7，p＝0.9五组数据对Krawtchouk多项式进行迭代计算测试。其相对误差如图2a所示，绝对误差如图2b所示。

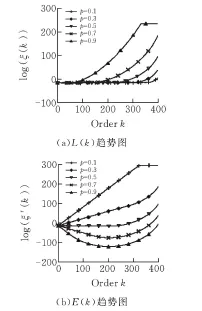
图2 Krawtchouk多项式迭代计算误差随阶数k变化图

由图2可知：当p取以上五个数据时其绝对误差和相对误差均是发散的，其递归误差在一定范围内无法得到抑制，因此Krawtchouk矩三项递归公式不具有数值稳定性，这与判据2所得出的结论完全相同，证明了判据2的可行性。

4 结论

本文从一个新的角度对正交矩三相递归式的稳定性做出了分析，给出了一种根据极限判断其数值稳定性的判据。对比文献［3］所提出的判据，该判据仅需判断三相递归式的计算系数极限存在与否即可判断其数值稳定性，因此可以更为灵活快捷地应用于正交矩稳定性分析中。目前仅有一类极限不存在但是不为无穷的三项多项式无法利用该判据判断稳定性，如何判断这一类三项多项式的稳定性也是笔者下一步研究的焦点问题。

［1］ Mukundan R，Ramakrishnan K R.Fast computation of legendre and zernike moments［J］.Pattern Recognition，1995，28（9）：1433－1442.

［2］ Amayeh G，Erol A，Bebis G，et al.Accurate and efficient computation of high order zernike moments［C］.ISVC 2005：462－469.

［3］ 郭浩，范秀香，付波，等.三项递归公式的数值稳定性分析［J］.湖北工业大学学报，2016（2）：58－61.

［4］ Mukundan R，Ong S H，Lee P A.Image analysis by tchebichef moments［J］.IEEE Transactions on Image Processing.2001，10（9）：1357－1364.

［5］ 程曹宗.应用泛函分析［M］.北京：机械工业出版社，2008.

［6］ Xiao B，Ma J F，Wang X.Image analysis by bessel–fourier moments［J］.Pattern Recognition，2010，43（8）：2620－2629.

［7］ Ziliang P，Rigeng W，Yunlong S.Image description with chebyshev－fourier moments.［J］.Journal of the Optical Society of America A Optics Image Science ＆Vision，2002，19（9）：1748－54.

［8］ Zhu H Q，Shu H Z，Liang L，et al.Image analysis by discrete orthogonal dual－hahn moments［J］.Pattern Recognition Letters.2007，28：1688－1794.

Numerical Stability Criterion of the Three Recursion Relations Based on Norm Measurement

FU Bo，HU Shi，ZHAO Xilin，，XU Guanghui
（School of Electrical and Electronic Engineering，Hubei Univ.of Tech.，Wuhan 430068，China）

Numerical stability analysis of orthogonal moments is one of the hot topics in the field of image analysis in recent years.This paper studies the most commonly used three recursive formulas among the orthogonal moments analytic ones.First，the concepts of three recursion formulas and numerical stability of orthogonal moments were introduced；Then a new stability criterion was proposed to judge the stability of three recursion relations based on Euclidean norm standard，which was proofed in detail；Finally，two examples were used to demonstrate the feasibility of this criterion.

three recursion relations of orthogonal moments；euclidean norm；limit of calculation factors；numerical stability

TP13

A

［责任编校：张岩芳］

1003－4684（2017）04－0035－04

2016－06－27

国家自然科学基金（61072130；51109088）；武汉市科技攻关计划项目（2013012401010845）；湖北工业大学科研基金项目（BSQD12107）；广东省工业攻关项目（2011B010100037）

付 波（1975－），男，湖北武汉人，工学博士，湖北工业大学教授，研究方向为图像处理