STORM原始图像和基于点扩散函数测量矩阵的压缩感知后处理方法
2017-09-18陈丹妮
程 涛,陈丹妮,于 斌
(1. 深圳大学光电工程学院光电子器件与系统(教育部/广东省)重点实验室,广东 深圳 518060;2. 广西科技大学汽车与交通学院,广西 柳州 545006;3.深圳大学光电工程学院深圳生物医学光学微纳检测与成像重点实验室,广东 深圳 518060)
STORM原始图像和基于点扩散函数测量矩阵的压缩感知后处理方法
程 涛1,2,3,陈丹妮1,3,于 斌1,3
(1.深圳大学光电工程学院光电子器件与系统(教育部/广东省)重点实验室,广东深圳518060;2.广西科技大学汽车与交通学院,广西柳州545006;3.深圳大学光电工程学院深圳生物医学光学微纳检测与成像重点实验室,广东深圳518060)
针对随机光学重构显微等超分辨率显微成像技术存在的图像采集重构慢、空间分辨率低、时间分辨率弱,基于点扩散函数测量矩阵的约束等距性差和重构效果不好等缺点,提出了随机光学重构显微(STORM)原始图像和基于点扩散函数测量矩阵的压缩感知后处理方法。仿真结果表明,该方法在不改变显微镜光学系统的前提下,通过对STORM原始图像和基于点扩散函数测量矩阵的后处理,能够大幅提高超分辨率显微成像的重构效果。
压缩感知;随机光学重构显微;点扩散函数;超分辨显微成像
OCIS编码(230.0230 Optical devices;220.0220 Optical design and fabrication;110.0110 Imaging systems)
0 引言
超分辨率显微成像能使人眼直接观察放大的微观过程和结构。超分辨率显微成像在生物、医学、材料、精密机械和微电子等领域有广泛的应用和需求,对于各学科工程和科学前沿问题的解决具有重大意义[1]。可见光波段的光学显微镜具有非接触、无损伤、可探测样品内部的优势,是研究器官、组织和细胞的重要工具[2]。由于衍射极限的存在,横向和纵向分辨率分别只有200 nm和500 nm[3]。超衍射极限的光学超分辨显微成像理论和技术一直是研究的热点。
近场光学成像利用近场倏逝波可获纳米量级的分辨率,尽管避免了远场衍射带来的Abbe分辨率极限,但仅限于细胞膜表面成像,无法用于活细胞和细胞内成像[1-2]。
远场突破衍射极限的荧光成像方法利用非线性效应对点扩散函数进行改造,通过缩小荧光光斑来提高空间分辨率达纳米水平。轴向分辨可达33~60 nm,横向分辨率可达16 nm[1]。尽管随机光学重构显微(Stochastic Optical Reconstruction Microscopy,STORM)和(荧光)光敏定位显微((Fluorescence) Photoactivated Localization Microscopy,(F)PALM)[1]可获得纳米分辨率的荧光图像[2],但也存在图像采集速度慢、采集过程复杂、图像重构速度慢、重构算法复杂、时间分辨率低等缺点。而且重构效果受稀疏激发时荧光分子分布情况的影响很大,当相邻荧光分子较近时空间分辨率会降低。如何克服当前技术的缺点,实现高速高效的超分辨率显微成像一直是人们期望的数据采集处理格局。尤其实现纳秒乃至皮秒量级时间分辨率的的高速高效超分辨率显微成像技术是人们一直渴望的[1]。
如能实现对视场所有荧光分子的同时激活/淬灭和一次采集就可以避免STORM和(F)PALM一次只能对一个或少数荧光分子作图像采集的重复繁琐工作,从而节约巨大的人力物力资源,缩短超分辨率成像的采集重构周期、极大提高时间分辨率、简化历史图像档案管理,减少数据量,对于噪声的处理和控制也能更加地简化。压缩感知技术的出现为解决STORM和(F)PALM等的问题和缺点提供了可能。本文针对此问题,提出了STORM原始图像和基于点扩散函数测量矩阵的压缩感知后处理方法。
1 基于压缩感知的超分辨率显微成像
根据压缩感知理论,如果信号(图像也是信号的一种)x是稀疏的,测量矩阵满足约束等距性(Restricted Isometry Property, RIP),那么求解式(1)就能以远低于Nyquist采样定理要求的采样率以极大概率实现对x的准确或近似重构。
min‖x‖0s.t.y=Φx
(1)
式中,y是测量数据;Φ既是测量矩阵,Φ∈RM×N(M 尽管不同重构算法对信号x的重构效果有很大的影响,但是测量矩阵Φ性能的好坏对信号x的重构效果的影响却是决定性的。如果测量矩阵各列和各行不相关性好,行模和列模近似相等,以及各行列元素具有一定的随机性,那么测量矩阵Φ就会具有较好的RIP性质,其中列的不相关性起主导作用[4-7]。 点扩散函数(Point Spread Function,PSF)是一个无限小物点通过光学系统(例如显微镜)在像平面处的光强分布函数[2]。光学系统的成像过程就是物函数与PSF的卷积,如果对物函数和PSF作离散化处理,那么物函数与PSF的卷积就相当于两个离散向量的内积。文献[8]基于这一原理,采用PSF构成压缩感知的测量矩阵Φ,以STORM低分辨率原始图像叠加后的合成图像作为测量数据y,采用CVX算法通过式(1)重构出x,最终得到一副21 nm的超分辨率图像x。在这一过程中测量数据采用的是STORM低分辨率原始图像叠加后的合成图像,这就意味着在真实试验中可以一次激活所有的荧光分子,而不必满足STORM要求的荧光分子稀疏激发和分时成像的要求。从而实现对所有荧光分子的一次激活或猝灭和一次测量,因此能获得极高的时间分辨率和图像的采集重构效率。 文献[8]以32×32像素的STORM叠加后的模拟原始图像为研究对象,每次以压缩感知算法CVX重构其中的8×8像素的子图。原始图像的每个像素被分成8×8网格,所有的仿真荧光分子随机地分布在各个网格中。PSF采用两个高斯函数叠加而成,标准差几乎为半个像素。为了尽量减少周边荧光分子的影响,只从8×8像素的子图中提取中间的7×7像素作为压缩感知的测量数据y,这时总计49个像素。采用的测量矩阵为Φ49×4096,Φ的大小为49行和4 096列。49行就是49个像素,对应原始图像;4 096列就是8×8像素子图的每个像素被分成8×8网格,这时总计有4 096个网格,对应超分辨(真实)图像x。 为了与文献[8]的实验结果和实验条件一致,我们的实验也采用文献[8]的参数设置,测量矩阵也采用Φ49×4096。为进一步就基于PSF的测量矩阵Φ的性能和改进方法做深入研究,我们以三种不同压缩比的基于PSF的测量矩阵Φ49×4096、Φ169×4096和Φ625×4096为研究对象。Φ169×4096和Φ625×4096对应的STORM叠加后的原始图像的分辨率分别比Φ49×4096高2和4倍(即显微镜采用的EMCCD记录相机的像素减小2倍和4倍)。对应Φ49×4096、Φ169×4096和Φ625×4096的超分辨图像x的网格大小不变,都是21 nm。 图1(a)和图2(a)是基于文献[8]在保持网格大小为21 nm时,基于PSF生成的测量矩阵灰度图,灰度图每个像素的灰度值对应测量矩阵该点元素的值。图1(a)是测量矩阵Φ169×4096,图2(a)是测量矩阵Φ625×4096。测量矩阵Φ49×4096的灰度图比图1(a)更加狭长,需要放大许多倍才能辨认,故未在文中展出。由图1(a)和图2(a)可见,基于PSF的测量矩阵的各行各列都非常相似,因而各行各列高度相关,RIP性质很差,非常类似阶梯矩阵。 图1 测量矩阵Φ169×4096的灰度图Fig.1 Gray image of the measurement matrix Φ169×4096 图2 测量矩阵Φ625×4096的灰度图Fig.2 Gray image of the measurement matrix Φ625×4096 压缩感知多研究的是RIP性质好的随机矩阵,对行列高度相关的RIP性质很差的基于PSF的测量矩阵(例如图1(a)和图2(a))的研究尚未见报道。当前基于压缩感知的超分辨率成像研究多集中于压缩感知在超分辨率成像中PSF的具体应用以及实验实现[9-11]。Elad[12]、Duarte[13-14]和赵瑞珍[15-16]等以各列相关性最小化或平均化为目标优化测量矩阵取得了很好的效果。如果采用这些优化方法,那就意味着需要根据优化后的测量矩阵设计新的显微镜(光学系统)。但是当采用的显微镜(光学系统)确定后,PSF就确定,无法再做改变,因此这些优化方法不适合基于PSF的测量矩阵。 由于基于PSF的测量矩阵行列高度相关,RIP性质很差,所以文献[8]的重构效果并不好。如能对STORM低分辨率原始图像和测量矩阵作后处理,就能显著提高重构效果和空间分辨率。本文在文献[8]的基础上开展21 nm高分辨率时的STORM低分辨率原始图像和PSF的后处理研究。本文所有计算和模拟都在Matlab2012中完成,操作界面如图3所示。 图3 计算软件操作界面Fig.3 Computing software interface 为了研究基于PSF的测量矩阵性质,表1列出了基于PSF的测量矩阵Φ和后处理后测量矩阵ΦT的各种统计学参数(表1中各列数据,除“Jarque-Bera检验”外,“/”号左边的数据表示最小值,“/”号右边的数据表示最大值;“Jarque-Bera检验” 列,“/”号左边的数据表示符合“Jarque-Bera检验”的列数;“/”号右边的数据表示符合“Jarque-Bera检验”的行数)。Jarque-Bera检验用于检验测量矩阵某行或某列元素是否服从高斯分布。 表1 后处理前后测量矩阵的相关参数 根据已有研究成果[17-23]可知,对测量矩阵作行正交化和行列模单位化处理能有效改善高斯矩阵的行列不相关性,以及行列模的相近性,从而改善测量矩阵的RIP性质。对基于PSF的测量矩阵做各行正交规范化和各列单位化的处理,都属于矩阵的初等变换。初等变换前后不会改变矩阵的秩,因此存在可逆矩阵P和Q使PΦQ=ΦO,ΦO是对Φ做各行正交规范化和各列单位化处理后的矩阵。 在几何物理意义上,P表示矩阵初等变换中的行变换;Q表示矩阵初等变换中的列变换。行单位化和正交化起主导地位;列单位化只起较小的作用。因此ΦT=TΦ≈PΦQ=ΦO,其中,T=ΦOΦT(ΦΦT)-1。 因此,我们设计的STORM原始图像和PSF的后处理方法和流程如下。在观察阶段采用显微镜以式(1)中的约束方程的形式采集低分辨率STORM图像;在后处理阶段以矩阵T对测量矩阵Φ和STORM低分辨率原始图像y做后处理,ΦT=TΦ,yT=Ty;在重构阶段以式(2)重构得到高分辨率图像x。 min‖x‖0s.t.yT=ΦTx,其中yT=Ty,ΦT=TΦ (2) 通过计算和实验发现,对基于PSF的测量矩阵连续进行各行正交规范化、各列单位化的循环迭代,一次循环迭代与多次循环迭代的结果并无显著差异。因此,PSF和STORM原始低分辨率图像的后处理算法如下: 输入:基于PSF的测量矩阵Φ,STORM原始图像y; 1)正交规范化Φ各行向量(且单位化Φ各列向量),得到矩阵ΦO; 2)ΦT=TΦ≈ΦO,其中,T=ΦOΦT(ΦΦT)-1; 3)yT=Ty; 输出:后处理后的测量矩阵ΦT和STORM低分辨率图像yT。 图1(a)的测量矩阵Φ169×4096进行各行正交规范化后的灰度图如图1(b)所示;图1(a)的测量矩阵Φ169×4096后处理(即图1(a)的测量矩阵Φ169×4096进行各行正交规范化后,再作各列单位化处理,最后求得ΦT)后的测量矩阵灰度图如图1(c)所示。图2(a)的测量矩阵Φ625×4096进行各行正交规范化后的灰度图如图2(b)所示;图2(a)的测量矩阵Φ625×4096后处理后的测量矩阵灰度图如图2(c)所示。图1(a)和图2(a)中包含大面积的黑色区域,黑色区域的灰度值为0。这说明图1(a)和图2(a)所表示的测量矩阵都是包含大量0的稀疏矩阵。图1和图2的(b)和(c)中没有黑色的区域。这说明图1和图2的(b)和(c)所表示的测量矩阵都是不包含0的稠密矩阵。 为了进一步验证后处理方法的有效性,图4—图6以OMP,BP和CVX算法计算后处理前Φ49×4096,Φ169×4096,Φ625×4096对相同信号集的测量重构实验结果。同时以矩阵T乘以基于PSF的测量矩阵Φ的测量值(yT=Ty),以后处理后的测量矩阵ΦT(ΦT=TΦ)和yT(yT=Ty)重构信号,同样将实验结果标示于图上。信号采用服从高斯分布的荧光分子稀疏信号,对每个稀疏度K值做500次试验,然后计算信号的精确重构概率。精确重构指的是重构信号和原始信号的信噪比(SNR)大于90 dB。SNR的计算公式: (3) 式中,x是真实信号,x∈RN, ‖g‖2是向量的l2范数,xR是x的重构结果。 图4—图6中的(a)、(b)和(c)图是采用OMP,BP和CVX算法对测量矩阵Φ49×4096,Φ169×4096和Φ625×4096及相应测量数据后处理前后的精确重构概率和信号稀疏度关系的实验曲线。 图4、图5和图6中“后处理后”曲线几乎都高于“后处理前”曲线。由表1可知,图6中测量矩阵后处理前后的列不相关性(0.999 613、0.906 178)好于图5(0.999 710、0.960 630),图5中测量矩阵后处理前后的列不相关性(0.999 710、0.960 630)远好于图4(0.999 976、0.999 923)。因此,图6测量矩阵Φ625×4096的性能优于图5,图5测量矩阵Φ169×4096的性能又远优于图4测量矩阵Φ49×4096。图6(b)中后处理曲线的精确重构概率都为0。图4(b)是图4—图6所有图中唯一一幅“后处理后”曲线劣于“后处理前”曲线。这是因为BP算法的默认迭代次数只有85步。从理论上说,后处理前后解空间不变,如果默认迭代步数足够大,图4(b)中的两条曲线应该重合。出现这种现象主要是因为图4中Φ49×4096的列不相关性在处后理前后几乎无变化(0.999 976、0.999 923),仅为0.000 053。 在图4—图6的OMP,BP和CVX三种算法中,CVX算法的重构效果最好。在图5(c)和图6(c)中,“后处理后”曲线几乎是一条精确重构概率为1的直线,远远高于“后处理前”曲线。即使在图4(c)中,“后处理后”曲线也较“后处理前”曲线有较大提高。因此,OMP,BP和CVX三种算法中,CVX最适合用于基于压缩感知的超分辨率显微成像重构。这是因为CVX相较于BP,在目标函数中引入了测量矩阵各列的权重。 图4 Φ49×4096后处理前后的精确重构概率与稀疏度的关系Fig.4 Prob. of exact recovery vs. the sparsity by before and after post processing 图5 Φ169×4096后处理前后的精确重构概率与稀疏度的关系Fig.5 Prob. of exact recovery vs. the sparsity by before and after post processing 图6 Φ625×4096后处理前后的精确重构概率与稀疏度的关系Fig.6 Prob. of exact recovery vs. the sparsity by before and after post processing 图7—图9是以CVX算法计算后处理前Φ49×4096、Φ169×4096和Φ625×4096对不同稀疏度信号的某次测量重构实验结果。图7(a)是15个荧光分子的真实位置;(b)是采用Φ49×4096模拟生成的STORM低分辨率原始图像;(c)是后处理前的重构结果,SNR为25.87 dB;(d)是后处理后的重构结果,SNR为40 dB。后处理前后,SNR提高14.13 dB。 图8(a)是36个荧光分子的真实位置;(b)是采用Φ169×4096模拟生成的STORM低分辨率原始图像;(c)是后处理前的重构结果,SNR为-9.97 dB,由图可见重构结果模糊不清,几乎无法识别;(d)是后处理后的重构结果,SNR为112 dB,图像非常清晰。后处理前后,SNR提高121.97 dB。 图9(a)是57个荧光分子的真实位置;(b)是采用Φ625×4096模拟生成的STORM低分辨率原始图像;(c)是后处理前的重构结果,SNR为-11.08 dB,由图可见重构结果模糊不清,几乎无法识别;(d)是后处理后的重构结果,SNR为129 dB,图像非常清晰。后处理前后,SNR提高140.08 dB。因此,通过对STORM低分辨率原始图像和PSF做后处理能大幅提高图像的重构效果和分辨率。基于PSF的测量矩阵性能是影响重构效果的关键因素。 图7 基于CVX和Φ49×4096的STORM图像分析Fig.7 STORM image analysis based on CVX and Φ49×4096 图8 基于CVX和Φ169×4096的STORM图像分析Fig.8 STORM image analysis based on CVX and Φ169×4096 图9 基于CVX和Φ625×4096的STORM图像分析Fig.9 STORM image analysis based on CVX and Φ625×4096 基于PSF的测量矩阵的压缩比(行列比)与测量矩阵的性能密切相关。但是也并非压缩比越小越好。对于测量矩阵Φ2401×4096,在重构计算过程中会涉及到大量的格罗姆矩阵的奇异值分解运算。由于Φ2401×4096各行列的不相关性突然变得很差,导致格罗姆矩阵几乎接近奇异化,从而导致计算机运算结果不准或错误,因而无法得到好的重构图像。而且随着测量矩阵规模的扩大,会导致运算速度以几何级数的方式降低。小的压缩比,意味着在现有显微镜获得基础上,只能得到较低的分辨率。当前对基于PSF的测量矩阵的理论分析和实验研究很少,因此准确把握和理解基于PSF的测量矩阵的性能需要做大量繁杂而深入的研究。 本文提出了STORM原始图像和基于点扩散函数测量矩阵的压缩感知后处理方法。该方法在无需对显微镜(光学系统)和观察对象改造和改进的前提下,实现了超分辨率显微成像重构效果的大幅提升。大大降低了显微镜的工程设计和实现难度,为进一步提高显微图像分辨率提供一条新的途径。仿真结果表明三种不同压缩比的基于点扩散函数测量矩阵Φ49×4096、Φ169×4096和Φ625×4096后处理后,精确重构概率大幅提高。在一组实验中SNR分别提高14.13 dB、121.97 dB和140.08 dB。 基于PSF的测量矩阵行列比与其性能有密切的关联。Φ169×4096的性能远远优于Φ49×4096。通过对Φ49×4096的STORM低分辨率原始图像做插值处理或提高现有显微镜的分辨率,有望获得和Φ169×4096一样或更好的重构效果和更高的分辨率。这也是我们下一步要开展的工作。 [1]牛憨笨, 陈丹妮, 尹君. 细胞内分子检测及成像技术研究 [J]. 深圳大学学报(理工版), 2011, 28(1): 1-16. [2]毛峥乐, 王琛, 程亚. 超分辨远场生物荧光成像——突破光学衍射极限 [J]. 中国激光, 2008, 35(09): 1289-1310. [3]吕志坚, 陆敬泽, 吴雅琼, 等. 几种超分辨率荧光显微技术的原理和近期进展 [J]. 生物化学与生物物理进展, 2009, 36(12): 1626-1624. [4]焦李成, 杨淑媛, 刘芳, 等. 压缩感知回顾与展望 [J]. 电子学报, 2011, 39(07): 1651-1662. [5]吴海佳, 张雄伟, 陈卫卫. 压缩感知新技术专题讲座(二) 第4讲 压缩感知理论中测量矩阵的构造方法 [J]. 军事通信技术, 2012, 33(1): 90-94. [6]张成, 杨海蓉, 韦穗. 确定性相位掩膜可压缩双透镜成像 [J]. 光子学报, 2011(6): 949-954. [7]刘吉英. 压缩感知理论及在成像中的应用 [D]. 长沙:国防科技大学,2010. [8]ZHU L, ZHANG W, ELNATAN D, et al. Faster STORM using compressed sensing [J]. Nature methods, 2012, 9(7): 721-723. [9]MENG J W L V, YING L, ET AL. Compressed-sensing photoacoustic computed tomography in vivo with partially known support [J]. Optics Express, 2012, 20(15): 16510-16523. [10]CHEN J, GONG W, HAN S. Sub-Rayleigh ghost imaging via sparsity constraints based on a digital micro-mirror device [J]. Physics Letters A, 2013, 377(31-33): 1844-1847. [11]GONG W, HAN S. Single-shot sub-Rayleigh imaging with pixel-limited detection [J]. Applied Physics Express, 2014, 7(6): 062503. [12]ELAD M. Optimized Projections for Compressed Sensing [J]. Signal Processing, IEEE Transactions on, 2007, 55(12): 5695-5702. [13]DUARTE-CARVAJALINO J M, SAPIRO G. Learning to sense sparse signals: simultaneous sensing matrix and sparsifying dictionary optimization [J]. Image Processing, IEEE Transactions on, 2009, 18(7): 1395-1408. [14]肖小潮, 郑宝玉, 王臣昊. 基于最优观测矩阵的压缩信道感知 [J]. 信号处理, 2012, 28(1): 67-72. [15]赵瑞珍, 秦周, 胡绍海. 一种基于特征值分解的测量矩阵优化方法 [J]. 信号处理, 2012, 28(5): 653-658. [16]LIFENG Y, GANG L, LIPING C. Optimizing projection matrix for compressed sensing systems[C]//proceedings of the Information, Communications and Signal Processing (ICICS) 2011 8th International Conference on.Singapore: IEEE, 2011:1-5. [17]DUARTE M F, DAVENPORT M A, TAKHAR D, et al. Single-pixel imaging via compressive sampling [J]. Signal Processing Magazine, IEEE, 2008, 25(2): 83-91. [18]AKCAKAYA M, JINSOO P, TAROKH V. A coding theory approach to noisy compressive sensing using low density frames [J]. Signal Processing, IEEE Transactions on, 2011, 59(11): 5369-5379. [19]付强, 李琼. 压缩感知中构造测量矩阵研究 [J]. 电脑与电信, 2011, 47(9): 39-41. [20]DONOHO D L, TSAIG Y, DRORI I, et al. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit [J]. Information Theory, IEEE Transactions on, 2012, 58(2): 1094-1121. [21]CANDES E J, TAO T. Near-optimal signal recovery from random projections: universal encoding strategies? [J]. Information Theory, IEEE Transactions on, 2006, 52(12): 5406-5425. [22]DONOHO D L. Compressed sensing [J]. Information Theory, IEEE Transactions on, 2006, 52(4): 1289-1306. [23]WEI D, MILENKOVIC O. Subspace pursuit for compressive sensing signal reconstruction [J]. Information Theory, IEEE Transactions on, 2009, 55(5): 2230-2249. 版权声明 凡稿件被本刊录用,即视为作者同意将该论文的复制权、发行权、信息网络传播权、翻译权、汇编权等权利在全世界范围内转让给本刊。本刊已许可中文科技期刊数据库、万方数据数字化期刊群、中国知网(中国学术期刊(光盘版)电子杂志社)和超星域出版系统在其各自的系列数据库产品中以数字化方式复制、汇编、发行及在信息网络传播本刊全文。作者著作权使用费和稿酬一并支付(即包括印刷版、光盘版和网络版各种使用方式的报酬)。如作者对本声明持有异议,请在投稿时说明。 本刊编辑部 CompressiveSensingPostProcessingofSTORM’sRawImagesandMeasurementMatrixBasedonPSF CHENG Tao1,2,3,CHEN Danni1,3,YU Bin1,3 (1.Key Laboratory of Optoelectronic Devices and Systems of Ministry of Education and Guangdong Province, Shenzhen University, Shenzhen 518060, China; 2. Automotive & Transportation Engineering Institute,Guangxi University of Science and Technology, Liuzhou, 545006, China; 3.Shenzhen Key Laboratory of Micro-Nano Measuring and Imaging in Biomedical Optics of Shenzhen,Shenzhen University, Shenzhen 518060, China) Stochastic optical reconstruction microscopy (STORM) and other super resolution microscopy imaging technology have shortcomings such as slow acquisition and reconstruction of images, low spatial and time resolution, bad restricted isometry property (RIP) and bad reconstruction effect. The compressed sensing post processing method of STORM raw images and measurement matrices based on Point Spread Function (PSF) was proposed. This method enabled the reconstruction effect of super-resolution microscopy imaging to be significantly improved and enhanced by postprocessing of STORM raw images and measurement matrices based on PSF under the premise of not changing microscope optical system. A new way was provided for improve the resolution of microscopic images. The simulation results showed that the accurate reconstruction probability of measurement matrices based on PSF of three different compression ratios was greatly improved after the processing. SNR was improved by 14.13 dB, 121.97 dB and 140.08 dB in a set of experiments respectively. compressive sensing;stochastic optical reconstruction microscopy;point spread function;super-resolution microscopy imaging 2017-02-21 :国家重点基础研究发展计划项目资助( 2012CB825802);国家自然科学基金资助项目(61335001, 61178080, 61235012, 11004136, 41461082, 81660296);国家重大科学仪器设备开发专项项目资助(2012YQ15009203);中国博士后科学基金项目资助(2016M592525);广西自然科学基金项目资助(2014GXNSFAA118285) :程涛(1976—),男,广西柳州人,博士,副教授,研究方向:压缩感知和超分辨显微。E-mail:ctnp@163.com。 TP391 :A :1008-1194(2017)04-0031-082 基于PSF的测量矩阵


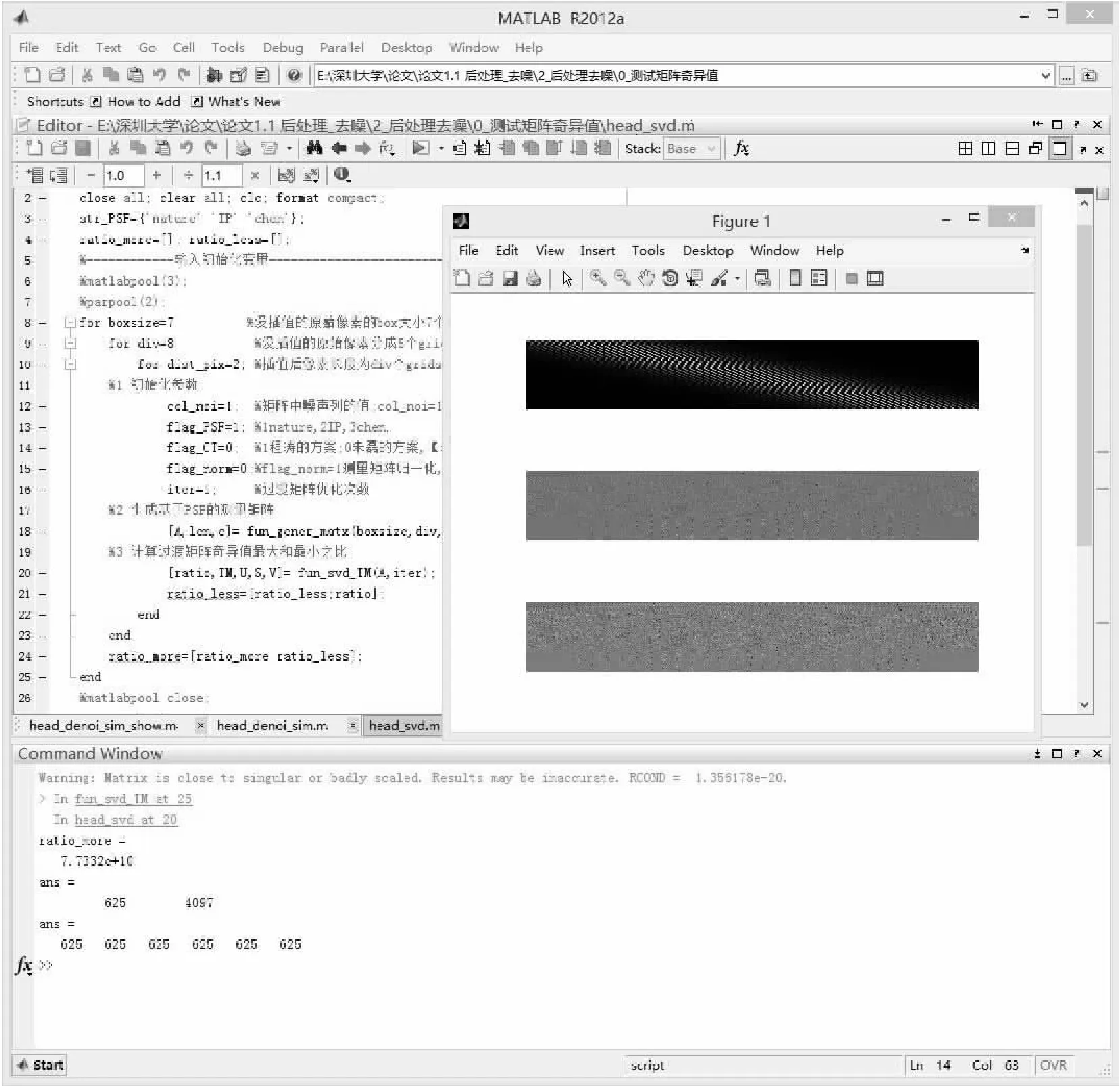
3 基于PSF的测量矩阵分析及后处理算法

4 信号重构结果对比及分析

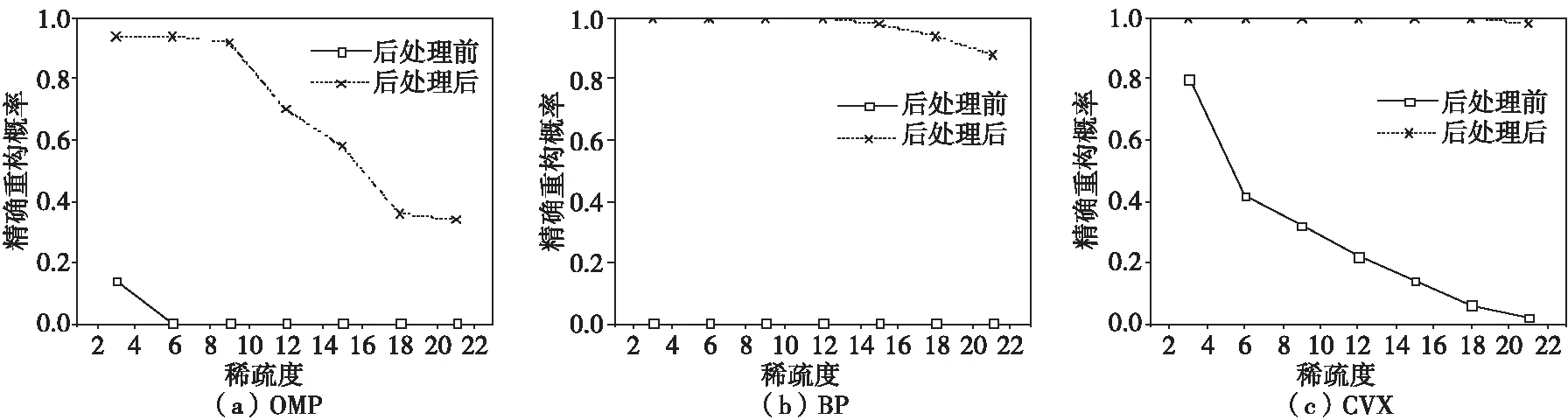



5 结论
