多样性度量的Top-K区分子图挖掘*

王章辉，赵宇海，王国仁，李 源

东北大学 计算机科学与工程学院，沈阳 110819

多样性度量的Top-K区分子图挖掘*

王章辉，赵宇海+，王国仁，李 源

东北大学 计算机科学与工程学院，沈阳 110819

图挖掘；图分类；子图模式；区分子图；多样性

1 引言

图数据是用来表示数据对象之间复杂关系的一种通用的数据结构，其广泛应用于各项科学研究领域中[1-3]。比如，在药物分子设计、蛋白质交互网络、社交网络等各项应用中，都使用图数据结构进行数据的分析与处理。

在大量图数据的应用中，经常使用不同的子图模式对图数据进行查询、管理与分析。频繁子图模式可以用来构建高效的索引结构，帮助用户查询管理大量的图数据[4-5]；显著子图模式可以帮助研究者对图数据进行深入的分析[6-8]；在大量的图数据中，区分子图模式可以用来构建有效的分类模型，从而帮助研究者快速地实现对海量图数据的分类[7]。总之，图数据中隐含的图模式信息可以帮助研究人员更好地分析、处理与理解这些图结构信息。因此，从图数据库中进行图模式的挖掘具有重要的研究意义和应用价值。

目前，已有的图模式挖掘工作主要集中在频繁子图模式挖掘与显著子图模式挖掘两方面。其中，频繁子图挖掘工作是基于用户给定的频繁度阈值，从图数据库中找到所有满足支持度阈值的子图模式，通常情况下，频繁子图挖掘会产生大量的子图模式，不利于后续的分析与应用。而显著子图模式基于一定的度量方法（如统计方法等），对搜索空间使用采样或者近似过滤的技术，从而减少目标输出图模式的数量[8]。

在图分类的相关研究中，区分子图作为一种具有显著区分能力的图模式，已有大量研究使用区分子图来构建高效的分类模型[6-9]。通常的做法首先从图数据库中挖掘Top-K个具有最大区分能力的图模式，而后利用这些图模式构建图分类模型。不幸的是，现有的区分子图挖掘算法往往只关心目标模式所具有的区分能力的大小，并以此作为选择是否输出的唯一标准。这显然会造成输出结果中存在一定的冗余图模式，不利于构建高效的图分类器。

在进行Top-K图模式的挖掘工作时，传统方法往往根据目标图模式度量值的大小进行排序，输出前K个目标图模式[10-11]。这些方法忽略了图模式之间的相关性：其一，这些图模式本身之间可能非常相似，当得到其中一个图模式后，就会对相似的图模式失去研究的意义，这与研究者希望得到多样化的输出结果相悖[12]；其二，在进行图分类应用中，虽然这些图模式的结构本身并不相似，但它们的支持集十分相似，从构建高效的图分类器的角度来讲，这将会造成大量的图特征的过拟合现象，从而不利于构建高效的图分类器。

为了克服传统Top-K图模式挖掘所面对的问题，本文提出了基于多样性度量的Top-K区分子图挖掘方法，其联合了结构多样性与支持集多样性的双重约束，避免了输出模式之间的相似、相关问题。本文首先讨论了结构相似性度量与支持集相似性度量，并结合二者给出了一个统一的多样性度量标准，从而实现了挖掘结果之间的结构多样性与支持集多样性。为了高效地实现挖掘多样性度量的Top-K区分子图，本文提出了两个算法Greedy-TopK与Leap-TopK。其中，Greedy-TopK算法采用两步的增量贪婪方法挖掘K个区分子图模式，即首先从图数据库中产生大量的区分子图模式，而后从这些区分子图中增量贪婪地得到K个多样性区分子图模式结果，当第一步得到的区分子图模式数量巨大时，Greedy-TopK方法会面对效率低与可扩展性差的问题。Leap-TopK避免了Greedy-TopK分两步方法的缺点，通过在挖掘过程中限制与结果集结构相似模式的扩展，实现了在搜索空间的跳跃搜索，从而避免了冗余模式的生成与计算工作，实现了在挖掘过程中增量地得到多样性度量的Top-K区分子图模式集合。显然，因为Leap-TopK方法通过一遍挖掘就可以得到结果，从效率方面要明显优于Greedy-TopK方法。

实验结果表明，本文提出的多样性度量的Top-K区分子图挖掘在结果质量与构建分类器的准确度方面都远远优于传统的区分子图挖掘方法。同时，Leap-TopK方法比Greedy-TopK方法拥有较高的运行效率。

本文组织结构如下：第2章介绍了区分子图挖掘的相关概念，并给出问题的形式化描述；第3章分别介绍两个多样性度量的Top-K区分子图挖掘算法Greedy-TopK和Leap-TopK；第4章通过实验对提出的算法进行有效性与高效性分析；第5章介绍相关工作；第6章对全文进行总结。

2 问题描述

本章首先介绍一些区分子图挖掘相关概念，接下来对多样性度量的Top-K区分子图挖掘进行形式化定义。

2.1 基础概念

本文主要考虑简单的连通无向标签图，一个标签图G可以定义为一个四元组G=(V,E,Σ,F)。其中，V是顶点集合；E⊆V×V是边集合；Σ是标签集合；F:V⋃E→Σ是一个函数，用来对图中顶点和边分配相应的标签。图G中边的集合可以用E(G)表示，|E(G)|则表示图G中边的数量。此外，一个图还可以属于唯一的类别。图1给出了一个二类示例图数据库 D，其中G1、G2、G3和G4属于正类图集合，用 D+表示；G5、G6、G7和 G8属于负类图集合，用 D-表示。本文算法采用二类图数据进行分析与研究，通过对算法进行简单的修改，其同样适用于多类图数据库。

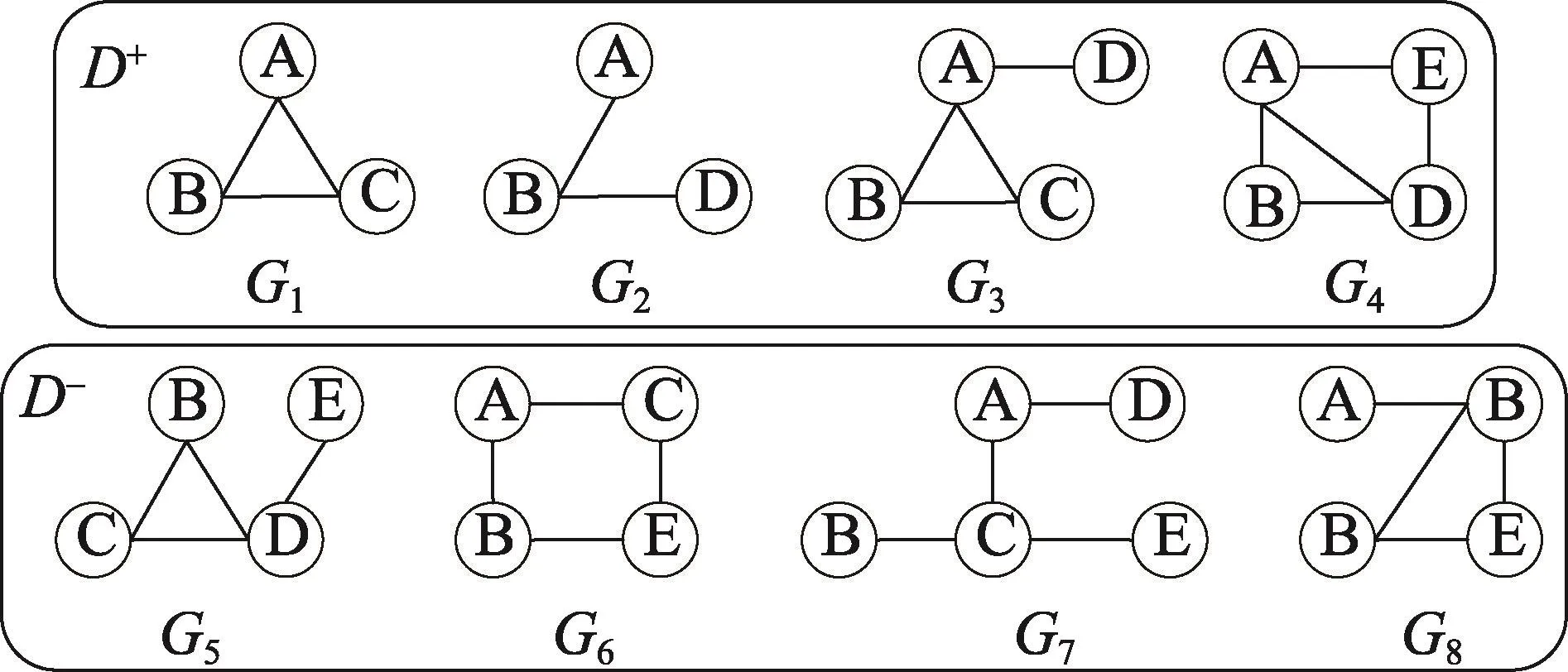
Fig.1 Graph database D图1 图数据库D

定义1（子图同构）给定两个图G1=(V,E,Σ,F)和 G2=(V′,E′,Σ′,F′)，如果存在一个映射函数 f:V→V′和G2的一个子图S，满足 f是从G1到S的同构，则称 f是一个从G1到G2的子图同构，也称G1子图同构于G2。

如果存在一个从G1到G2的子图同构，称G1是G2的子图，G2是G1的超图或者G2支持G1，表示为G1⊆G2。

定义2（频繁度）给定一个图数据库D=D++D-={G1,G2,…,Gn}和一个图模式g，支持图模式g的集合记作Cov(g)={Gi|g⊆Gi,Gi∈D}。图模式 g的支持度为|Cov(g)|，表示为sup(g)；图模式g在图数据库的频繁度为|Cov(g)|/|D|，表示为 freq(g)。

同理，freq(g,D+)表示图模式g在正类图集合中的频繁度；freq(g,D-)表示图模式g在负类图集合中的频繁度。

定义3（区分子图）给定一个子图模式g，其在正类图集合中的频繁度远远高于其所在负类图集合中的频繁度，称该子图模式g为区分子图模式，为表达方便，简称为区分子图。

区分子图g的区分能力函数可以用式（1）来计算，dscore(g)取值越大，说明其具有的区分能力越大。为了避免分母为0的现象，可以为图数据库中负类图集合添加一个包含所有子图模式的图。

区分子图挖掘问题就是从一个给定的图数据库中，按照给定的区分能力函数，把dscore值大于0的所有子图模式都挖掘出来的过程。而对于Top-K区分子图挖掘则是按照每个子图的dscore值的大小进行排序，选择取值最高的前K个子图的挖掘过程。

2.2 问题定义

本节给出了多样性度量的Top-K区分子图挖掘问题。首先引入图结构相似性与支持集相似性概念，接下来给出图的相关性与多样性描述，最后给出本文的全局目标。

定义4（图结构相似性）给定两个子图模式g1与g2，其结构相似性表示两个子图模式在结构方面的相似度，可以用式（2）来表示。

两个子图的结构相似性可以用两个子图模式边的Jaccard关联系数来表示，该系数越大，说明这两个子图模式从结构上越相似。

定义5（图支持集相似性）给定两个子图模式g1与g2，其支持集相似性表示两个子图模式在支持集方面的相似度，可以用式（3）来表示。

与图的结构相似性类似，图的支持集相似性同样用它们的Jaccard关联系数来表示，相对较大的关联系数表明它们具有比较相似的支持集。

给定两个子图模式的结构相似性与支持集相似性的定义，就可以设计一个度量标准来对两个子图的相关性进行综合度量。本文引入一个λ变量来综合考虑两个子图模式在结构与支持集方面相似性的影响程度，两个子图模式g1与g2的相关性可以用式（4）来表示。

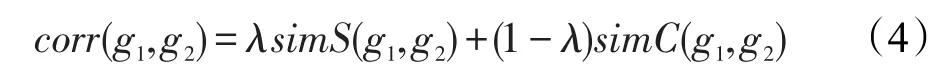
通常情况下，λ的取值为0.5，表示综合考虑了两个子图模式的结构相似性与支持集相似性。本文如无特殊说明，λ取值为0.5。

给定一组子图模式，显然任意两个子图模式g1与g2的偏离程度（多样性）可以用式（5）来表示。

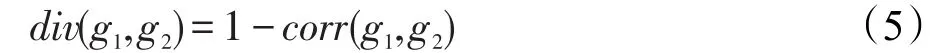
通常情况下，两个子图的div偏离程度值越小，说明两个子图的相关性越小。当div值选择为1时，说明这两个子图没有任何的相关性。通常情况下，选择一个小于1的实数，本文默认选择div的取值为0.8。在给定的一组子图模式中，任意两个子图模式的偏离值都大于0.8时，则说明它们之间具有较大的偏离程度，这样的一组子图模式可以称为具有多样性的子图模式组。

问题定义：给定一个图数据库D，一个指定的K值与div值，多样性度量的Top-K区分子图挖掘问题是找到一个子图模式集合S(1≤|S|≤K)，该子图模式集合S满足以下3条标准：

（1）1≤|S|≤K

（2）∀g1⊂S,g2⊂S,div(g1,g2)≥div

（3）max∑g⊂Sdscore(g)

多样性度量的Top-K区分子图挖掘需要找到一组不多于K个子图模式的结果集合，其中任意一个子图模式都是一个区分子图模式，并且要求结果集的区分能力之和是最大的；任意两个子图模式都是不相关的，是具有一定偏离度的；最大化一组子图模式的区分能力和是一个NP-难问题，该问题可以通过最大覆盖问题进行规约。

3 多样性度量的Top-K区分子图挖掘

既然多样性度量的Top-K区分子图挖掘问题是一个NP-难问题，因此需要设计近似算法或者启发式算法进行求解。本文提出了两个高效算法Greedy-TopK与Leap-TopK进行多样性的Top-K区分子图挖掘。其中Greedy-TopK方法采用两阶段的策略，而Leap-TopK方法通过在挖掘过程中限制与结果集结构相似模式的扩展，实现了在搜索空间的跳跃搜索，从而避免了冗余模式的生成与计算。

3.1 Greedy-TopK算法

Greedy-TopK算法采用的是两阶段的贪婪式搜索方法，如算法1所示。其首先需要通过某个区分子图挖掘算法[13-14]从图数据库中挖掘出大量的区分子图集合F；接下来按照每个区分子图的区分能力从大到小进行排序；最后从区分子图集合F中增量地选择K个具有多样性度量标准的区分子图。

算法1 Greedy-TopK算法

输入：图数据库D、K值与div值。

输出：多样性的最大化区分能力之和的K个区分子图集合S。

1.挖掘大量区分能力大于0的区分子图模式集合F；

2.对集合F中的区分子图按照区分能力从大到小进行排序；

3.S=∅；

4.if|S|＜Kdo

5.如果F为空集，则退出；

6.从F中选择一个区分能力最大的子图模式g，并把g从F中删除；

7.如果g与S中的子图模式满足多样性约束，并且可以增大S的区分能力之和；

8. S=S⋃{g}；

9.end if

10.输出集合S。

在增量地选择K个区分子图时，既要考虑最大化结果集合S的区分能力之和，还要同时保证结果集合S中任意两个区分子图都是不相关的（即结果集具有多样性）这两个标准。

3.2 Leap-TopK算法

Greedy-TopK算法是一种两阶段算法，其实现首先需要产生大量具有区分能力的子图模式。在第一阶段产生的区分子图数量规模不大的情况下，Greedy-TopK算法具有较高的效率。而当第一阶段区分子图挖掘算法产生大量的子图模式时，使得Greedy-TopK算法在效率方面面对极大的挑战，往往不能在合理的时间内完成算法，限制了该算法的可扩展性和可用性。针对Greedy-TopK算法存在的不足，本节提出了高效的Leap-TopK算法。

Leap-TopK算法是一个整体的算法，通过在挖掘过程中限制与当前结果集结构相似模式的扩展，实现了在搜索空间的跳跃式搜索，从而避免了冗余模式的生成与计算工作，实现了在挖掘过程中增量地得到多样性度量的Top-K区分子图模式集合。

Leap-TopK算法首先是一种图模式的分支界限搜索算法，因此其需要采用一种具体的搜索框架，用来确保目标模式可以被搜索与发现，在搜索框架的基础上，可以应用各种削减策略加速搜索过程的完成。DFS（depth first search）编码树搜索框架是一种高效的并得到广泛应用的搜索框架[5]。在DFS编码搜索树中，可以使用最小DFS编码实现图同构问题的检测。Leap-TopK算法在挖掘多样性度量的Top-K区分子图时，采用DFS编码树搜索框架进行子图模式的搜索。

Leap-TopK算法维护一个大小为K的小顶堆作为结果集S，其中堆顶元素为堆中dscore值最小的区分子图。在搜索子图模式空间时，逐渐产生K个互不相关的区分子图模式加入堆中；接下来计算新产生的子图模式区分能力dscore值的大小，并与堆顶的区分子图相比较，如果dscore值大于堆顶区分子图的dscore值，则需要根据其与结果集中已有的区分子图模式的相关性来决定是否添加并更新结果集S。

性质1在进行区分子图模式空间搜索时，如果当前子图模式g与结果集S中的任一子图模式g′的图结构相似性大于一定阈值，则可以直接跳过该子图模式的计算过程，该阈值可以通过式（6）得到。

证明 当前子图模式g如果要添加或者更新结果集S，则必须要求与结果集S内元素首先是不相关的，要求任意 div(g,g′)g′⊂S=1-corr(g,g′)g′⊂S≥div ，则corr(g,g′)g′⊂S≤1-div。而任意两个子图的相关性由式（4）可知，包含图结构相似性与图支持集相似性两部分，因为图支持集相似性是非负的，所以可以得出λsimS(g,g′)g′⊂S≤1-div，即要求两个子图模式的结构相似性

当进行区分子图模式空间搜索时，每扩展生成一个新的子图模式时，首先需要计算生成的子图模式与当前结果集S中的子图模式的图结构相似性值，如果与结果集S中的子图模式存在相关性大于式（6）这个阈值的情况，则可直接跳过该子图模式的计算过程，用来加速搜索过程的完成。

Leap-TopK算法的技术集成在gSpan[5]的DFS编码搜索框架中，完整算法如算法2所示。首先算法需要维护一个大小为K的小顶堆作为结果集S，初始化该集合为空。接下来遍历搜索DFS编码树生成子图模式，生成K个互不相关的区分子图加入结果集S中，并按照它们的dscore值的大小调整堆。当产生一个新的子图模式时，需要按照性质1判断该子图模式是否与结果集S中的子图模式结构相似，从而判断该子图模式是否可以直接被削减。当该子图与结果集S中的子图模式结构并不相似时，则需要计算它的dscore值，如果dscore值大于堆顶元素的dscore值，并且满足问题定义的第2条标准，则需要把该子图模式加入并替换结果集，同时对新结果集合S进行堆更新。

算法2 Leap-TopK算法

输入：图数据库D、K值与div值。

输出：多样性的最大化区分能力之和的K个区分子图集合S。

1.大小为K的堆S=∅；

2.搜索DFS编码树；

3.产生一个新的子图模式g；

4.按照性质1与式（6）进行削减；

5.获得一个与结果集S不相关的区分子图g；

6.如果|S|≠K并且满足问题定义的第2条标准，则S=S⋃{g}并调整结果集堆S；

7.如果g的dscore值大于集合S中堆顶元素的dscore值并且满足问题定义的第2条标准，S=S⋃{g}并调整结果集堆S；

8.end搜索结束；

9.输出集合S。

4 实验结果及分析

本文进行了大量的实验来考察提出算法的高效性和有效性，以及不同参数对算法的影响。本文算法采用基于标准模板库（STL）的C++编程实现，实验环境为联想PC机器，3.5 GHz双核处理器，4 GB内存，Window 7操作系统。

4.1 实验数据集

本文采用了PubChem（http://pubhem.ncbi.nlm.nih.gov）数据库上的一系列图结构数据集作为实验数据集。PubChem数据库是一个维护良好的记录生物活动的平台，包括各种分子生物活性检测、抗癌生物检测等记录。其中每个数据集根据其抗癌检测可以分为活跃和不活跃两类，表1对11个美国国家癌症研究所（NCI）检测数据集进行简单介绍。

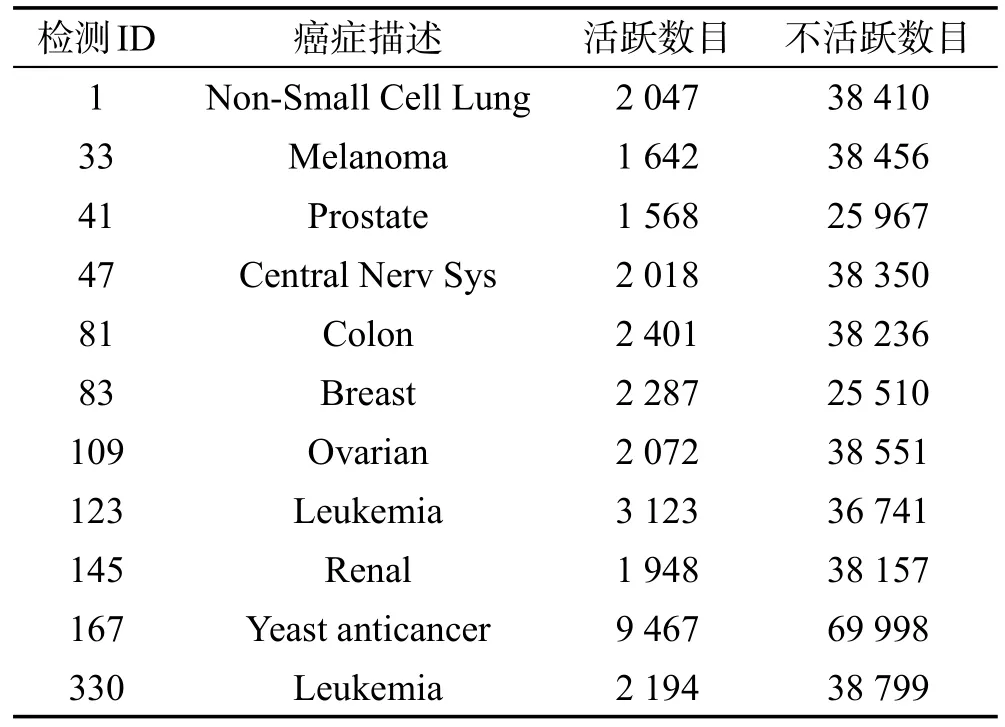
Table 1 Anti-cancer screen datasets表1 抗癌检测数据集

从表1中可以看出，每一种癌症检测活跃化合物的数目都远远小于不活跃化合物的数目，比例大约只占5%。大量区分子图挖掘算法[9,13-14]中实验部分均采用等比例的数据集，因此对每一个癌症检测数据集都随机选择1 000个活跃化合物和1 000个不活跃化合物组成新的平衡数据集。这样就重新组成11个规模为2 000的二类图数据集。接下来的实验中，均采用重新组合的数据集来度量本文算法的各项性能。

4.2 算法的效率

在进行算法效率分析实验时，由于Greedy-TopK算法是一种两阶段算法，其首先需要由已有的区分子图挖掘算法得到大量的区分子图，才能从这些区分子图中贪婪地选择K个多样性的区分子图结果集。在Greedy-TopK算法生成大量区分子图阶段，本文采用高效率的 LTS（learning to search）算法[14]为Greedy-TopK算法生成大量的区分子图，每次实验中都默认产生1 000个区分子图作为Greedy-TopK算法的候选区分子图集合。本文实验中所用到的参数变化及参数默认取值如表2所示，其中黑体数值代表相应参数默认的取值。

在进行算法的效率分析时，因为Greedy-TopK算法需要借助LTS算法生成的区分子图集合才能完成，所以Greedy-TopK算法的运行时间包括LTS算法生成区分子图集合的时间。首先比较了Greedy-TopK算法和Leap-TopK算法在检测ID 1生成的平衡数据集上随着K值变化的运行效率。从图2中可以看出，Leap-TopK算法明显优于Greedy-TopK算法，这得益于Leap-TopK算法的整体性和使用的结构相似性削减及跳跃式搜索，极大地缩减了算法的运行时间。同时，Greedy-TopK算法受K值变化的影响不大，这也说明了Greedy-TopK算法所需要的大量时间是在LTS算法产生大量区分子图候选集合阶段，而在贪婪查找K个多样性的区分子图时耗时随K值变化影响不大。

Table 2 Experimental parameter values表2 实验参数值

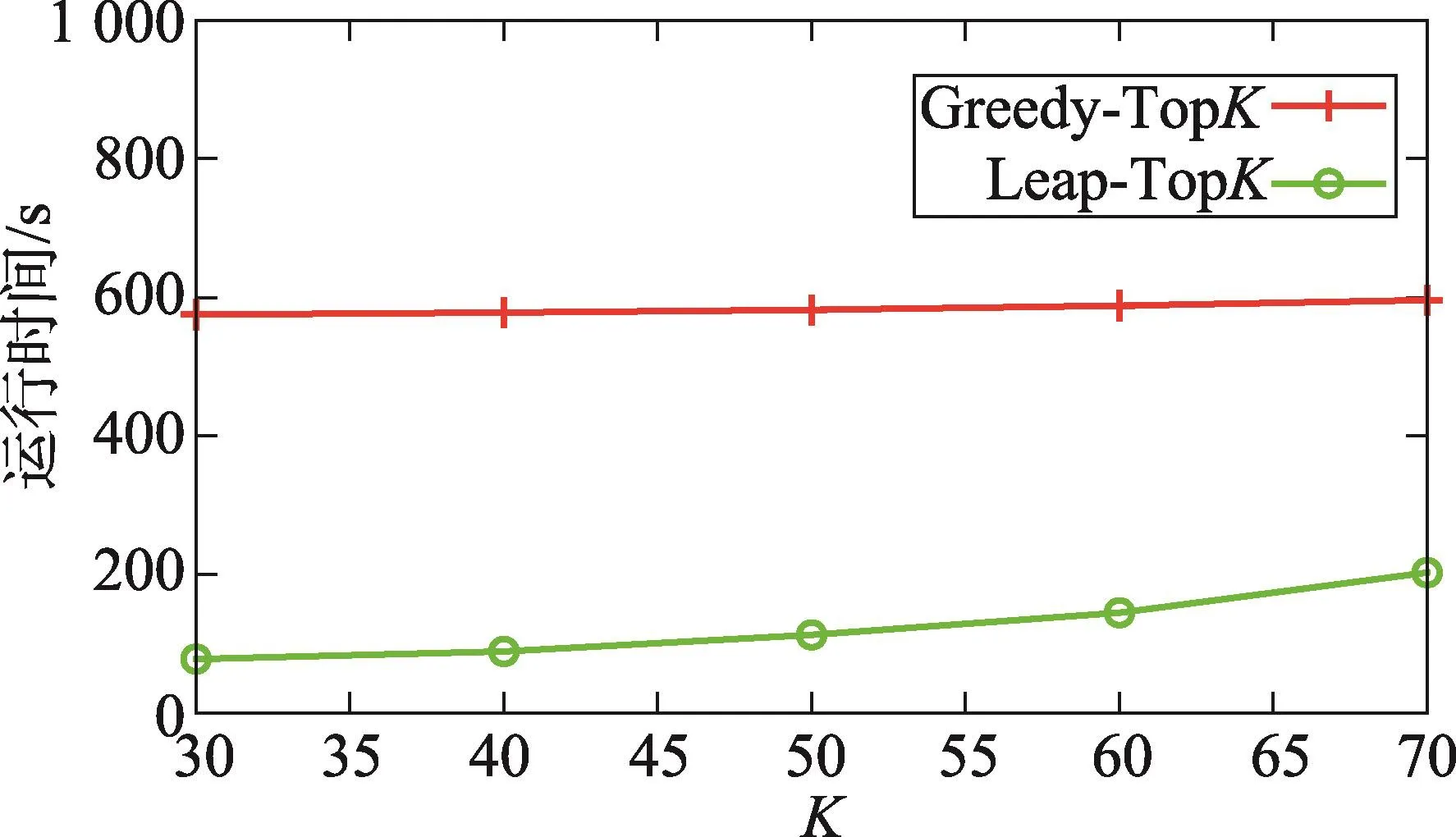
Fig.2 Runtime vs.varying K图2 K值变化时的执行时间

从图3中算法运行时间可以看出，Greedy-TopK算法与Leap-TopK算法的运行时间都随着多样性div值的变大而增加，即随着对多样性要求越严格（div值越大），两种算法所需要的执行时间都呈现显著增大的趋势。

同时对在表1中对应数据集生成的11个新的平衡数据集进行运行效率的对比。对LTS算法生成的1 000个区分子图按照区分能力大小排序，取前K个区分子图的方式得到对应的LTS-TopK算法。从图4中可以看出，Greedy-TopK算法在所有数据集上都具有较高的执行效率，而LTS-TopK算法与Greedy-TopK算法在绝大多数数据集上拥有相当的执行效率。

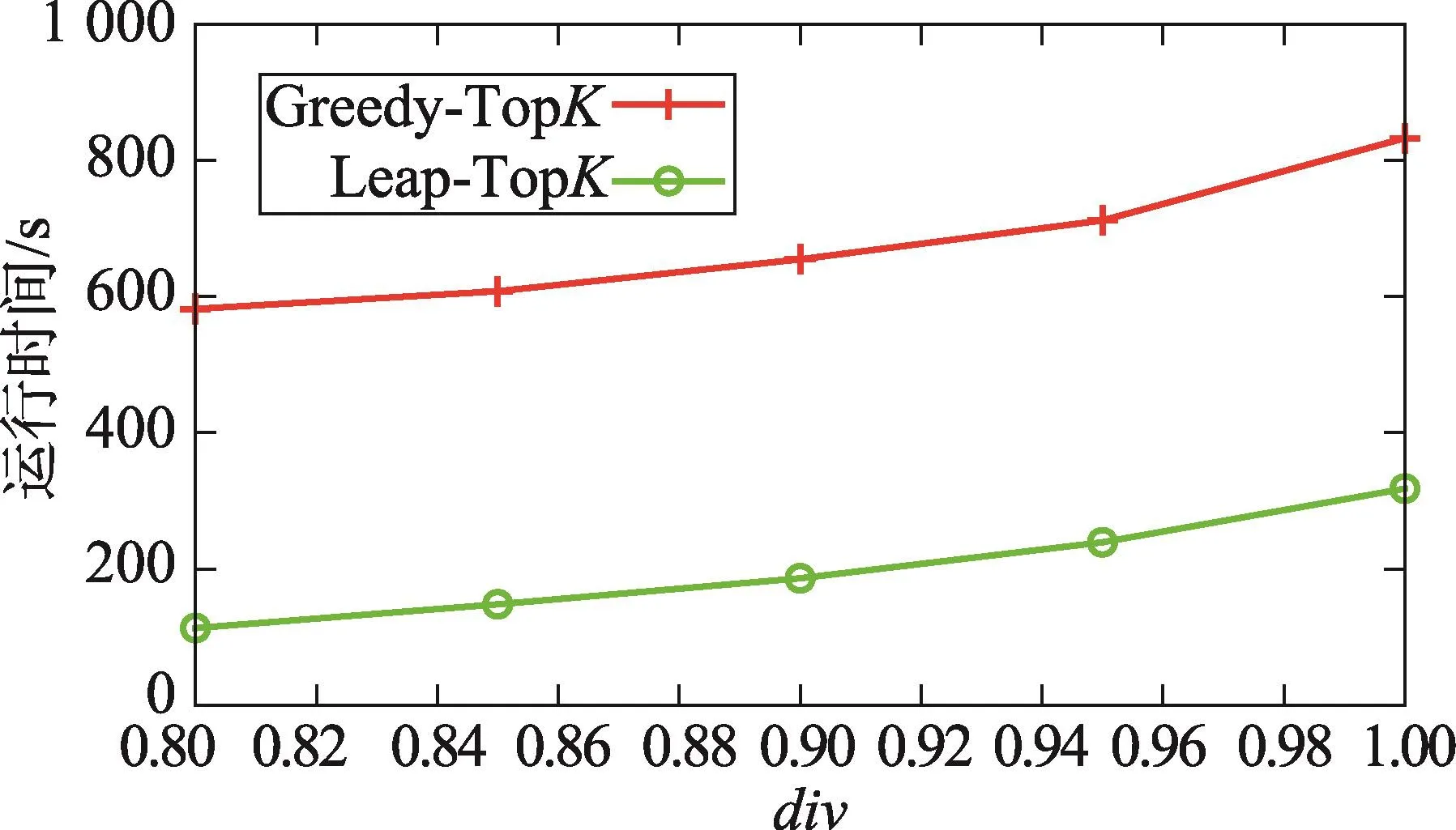
Fig.3 Runtime vs.varyingdiv图3 div值变化时的执行时间

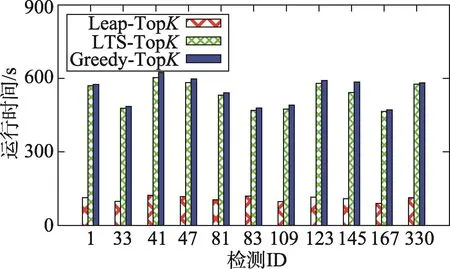
Fig.4 Runtime comparison in different datasets图4 在不同数据集上的执行时间对比

4.3 算法的有效性

首先对本文提出的两种挖掘多样性度量的Top-K区分子图算法所产生的输出结果数量随着div值的变化进行了实验，其中K值的默认值为50，实验结果是在11个数据集上得到的平均值。

从图5中可以看出，随着div值的增大，也就是随着对多样性度量标准的增加，Greedy-TopK算法不能很好地进行工作，也就是输出的区分子图模式数量远远低于指定的K值，尤其当div值选择为1时，Greedy-TopK算法的输出结果显得更加糟糕。而Leap-TopK算法相比较Greedy-TopK算法有一定的改善，特别当div多样性度量约束稍加放松时表现得更加明显。

最后，从分类应用的角度出发，进一步考察本文算法的有效性。基于算法得到的K个区分子图模式和支持向量机算法，可以构建相对应的图分类器，对数据集中的测试集进行分类评价。本文使用参数C介于[2-10,210]的支持向量机LIBSVM（http://www.csie.ntu.edu.tw/～cjlin/libsvm/）构建图分类器，通过构建的图分类器在测试数据集上的分类精度对比，证明本文算法的有效性。为了避免单次实验的偶然性，所有实验均重复进行5次，并进行平均计算。

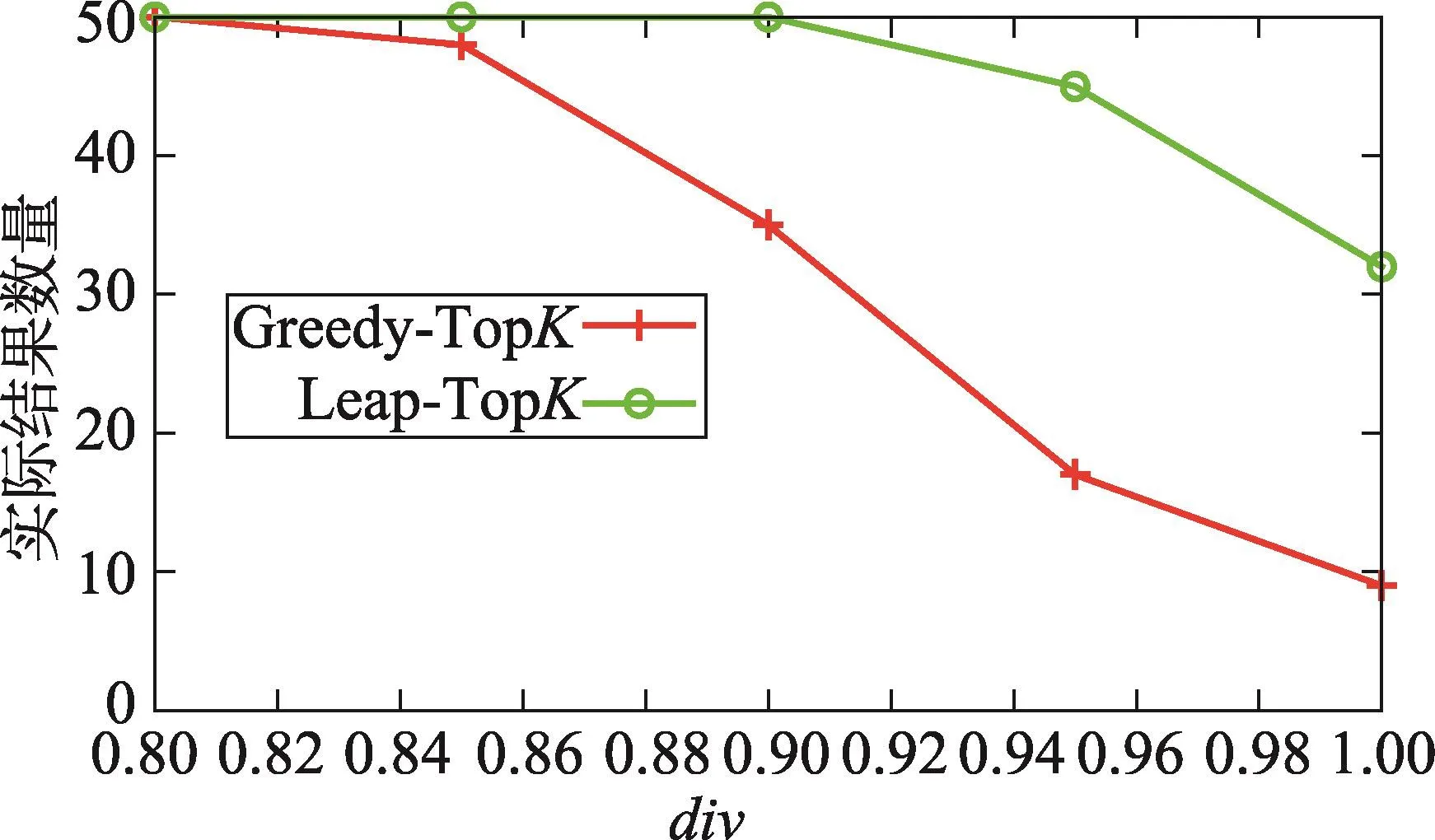
Fig.5 Result number vs.varyingdiv图5 div值变化时结果数量

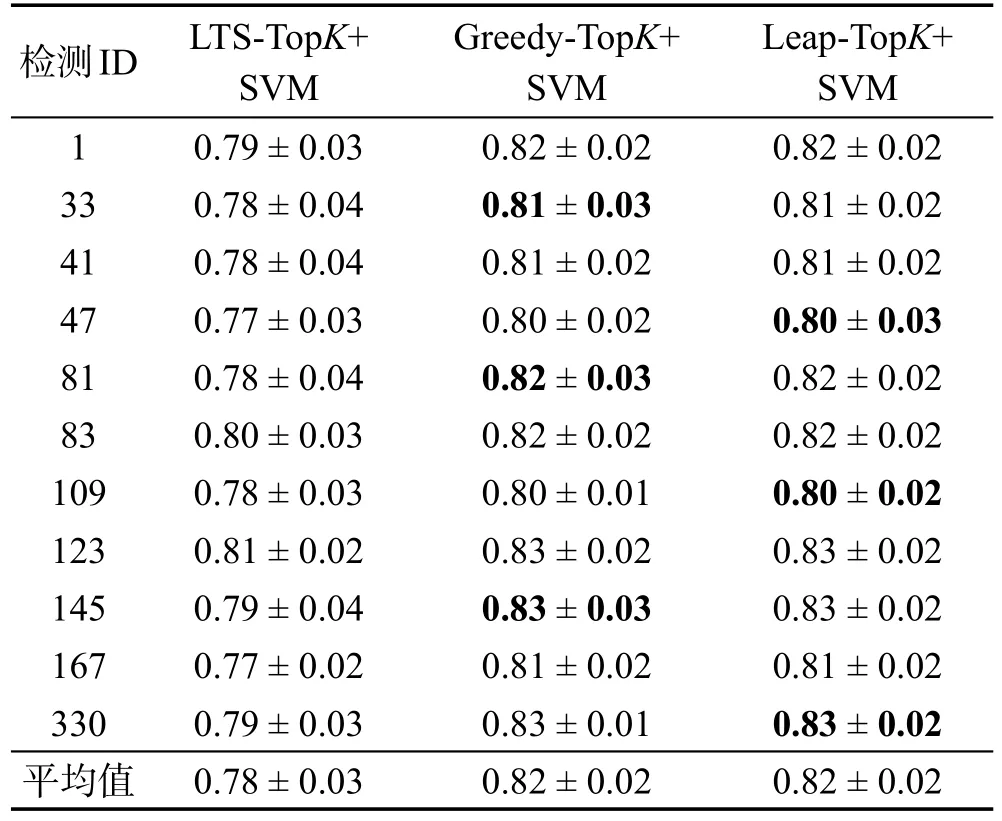
Table 3 AverageAUCscores表3 AUC平均得分

本文使用接收者操作特征（ROC）曲线下的面积（AUC）[6]作为分类精度的度量标准。AUC是一个介于0到1之间的实数，数值越大，说明分类器的分类精度越高，一个好的分类器产生的AUC值接近于1。

表3给出了使用3种算法产生图模式利用SVM算法构建的图分类器在不同数据集上的平均分类精度。从表3中可以看出，基于Greedy-TopK算法产生的区分子图模式的平均分类精度基本与Leap-TopK算法相当，但二者都明显优于LTS-TopK算法产生的分类精度。这就说明多样性度量的区分子图更加有利于构建高效的图分类器。同时也说明Leap-TopK算法与Greedy-TopK算法所产生的结果集质量差异不大，并且具有十分接近的分类性能。

5 相关工作

近年来，区分子图模式挖掘问题的相关研究一直备受众多研究者的关注[6-7,9,13-14]。文献[15]介绍了从频繁子图挖掘区分子图模式的方法，虽然这种方法可以获得所有的区分子图模式，但是十分浪费时间。文献[16]采用一定数量的对应组度量子图模式的区分能力，可以获得理论上的最优结果。文献[7]使用相对高支持度阈值从小规模数据组中挖掘区分子图模式。文献[6]基于结构近似导致区分能力近似的假设，大幅度削减模式搜索空间，快速得到挖掘结果。以上所有区分子图模式挖掘算法都未考虑挖掘结果之间可能出现高度相关的情况。而关于挖掘结果多样性的研究越来越得到研究者的关注，大量优秀的研究成果表明，多样性的挖掘可以提高结果的可分析性与可利用性[17-19]。目前为止，多样性的区分子图模式挖掘问题尚未得到广泛的研究。

6 结束语

本文提出了多样性度量的Top-K区分子图挖掘问题，并给出两个高效算法Greedy-TopK和Leap-TopK挖掘多样性度量的Top-K区分子图。实验结果表明，Leap-TopK算法的效率明显优于两阶段的Greedy-TopK算法。在可用性方面，利用Leap-TopK算法与Greedy-TopK算法挖掘结果构建的图分类器具有相似的分类精度，且都优于传统区分子图挖掘算法产生的结果，从而证明了提出的多样性度量Top-K区分子图挖掘算法的有效性。

接下来的研究工作侧重于处理大规模图数据的分类问题，包括大规模数据处理框架设计，统计显著性区分子图挖掘方法等方面。

[1]Huan Jun,Wang Wei,Bandyopadhyay D,et al.Mining protein family specific residue packing patterns from proteinstructure graphs[C]//Proceedings of the 8th Annual International Conference on Research in Computational Molecular Biology,San Diego,USA,Mar 27-31,2004.New York:ACM,2004:308-315.

[2]Borgelt C,Berthold M R.Mining molecular fragments:finding relevant substructures of molecules[C]//Proceedings of the 2002 IEEE International Conference on Data Mining,Maebashi City,Japan,Dec 9-12,2002.Washington:IEEE Computer Society,2002:51-58.

[3]Deshpande M,Kuramochi M,Wale N,et al.Frequent substructure-based approaches for classifying chemical compounds[J].IEEE Transactions on Knowledge and Data Engineering,2005,17(8):1036-1050.

[4]Kuramochi M,Karypis G.Frequent subgraph discovery[C]//Proceedings of the 2001 International Conference on Data Mining，San Jose,USA,Nov 29-Dec 2,2001.Washington:IEEE Computer Society,2001:313-320.

[5]Yan Xifeng,Han Jiawei.gSpan:graph-based substructure pattern mining[C]//Proceedings of the 2002 International Conference on Data Mining,Maebashi City,Japan,Dec 9-12,2002.Washington:IEEE Computer Society,2002:721-724.

[6]Yan Xifeng,Cheng Hong,Han Jiawei,et al.Mining significant graph patterns by leap search[C]//Proceedings of the 2008 International Conference on Management of Data,Vancouver,Canada,Jun 9-12,2008.New York:ACM,2008:433-444.

[7]Ranu S,Singh A K.Graphsig:a scalable approach to mining significant subgraphs in large graph databases[C]//Proceedings of the 2009 International Conference on Data Engineering,Shanghai,Mar 29-Apr 2,2009.Washington:IEEE Computer Society,2009:844-855.

[8]Hasan M A,Zaki M J.Output space sampling for graph patterns[J].Very Large Database Endowment,2009,2(1):730-741.

[9]Jin Ning,Young C,Wang Wei.Graph classification based on pattern co-occurrence[C]//Proceedings of the 18th Conference on Information and Knowledge Management,Hong Kong,China,Nov 2-6,2009.New York:ACM,2009:573-582.

[10]Zhu Yuanyuan,Qin Lu,Yu J X,et al.Finding top-k similar graphs in graph databases[C]//Proceedings of the 15th International Conference on Extending Database Technology,Berlin,Mar 27-30,2012.New York:ACM,2012:456-467.

[11]Ding Bolin,Yu J X,Wang Shan,et al.Finding top-k mincost connected trees in databases[C]//Proceedings of the 23rd International Conference on Data Engineering,Istanbul,Turkey,Apr 15-20,2007.Washington:IEEE Computer Society,2007:836-845.

[12]Fraternali P,Martinenghi D,Tagliasacchi M.Top-k bounded diversification[C]//Proceedings of the 2012 International Conference on Management of Data,Scottsdale,USA,May 20-24,2012.New York:ACM,2012:421-432.

[13]Jin Ning,Young C,Wang Wei.GAIA:graph classification using evolutionary computation[C]//Proceedings of the 2010 International Conference on Management of Data,Indianapolis,USA,Jun 6-10,2010.New York:ACM,2010:879-890.

[14]Jin Ning,Wang Wei.LTS:discriminative subgraph mining by learning from search history[C]//Proceedings of the 27th International Conference on Data Engineering,Hannover,Germany,Apr 11-16,2011.Washington:IEEE Computer Society,2011:207-218.

[15]Thoma M,Cheng H,Gretton A,et al.Discriminative frequent subgraph mining with optimality guarantees[J].StatisticalAnalysis and Data Mining,2010,3(5):302-318.

[16]Thoma M,Cheng Hong,Gretton A,et al.Near-optimal supervised feature selection among frequent subgraphs[C]//Proceedings of the 2009 International Conference on Data Mining,Sparks,USA,Apr 30-May 2,2009.Philadelphia,USA:SIAM,2009:1076-1087.

[17]Qin Lu,Yu J X,Chang Lijun.Diversifying top-k results[J].Proceedings of the VLDB Endowment,2012,5(11):1124-1135.

[18]Huang Xin,Cheng Hong,Li Ronghua,et al.Top-k structural diversity search in large networks[J].Proceedings of the VLDB Endowment,2013,6(13):1618-1629.

[19]Yuan Long,Qin Lu,Lin Xuemin,et al.Diversified top-k clique search[C]//Proceedings of the 31st International Conference on Data Engineering,Seoul,Apr 13-17,2015.Piscataway,USA:IEEE,2015:387-398.

WANG Zhanghui was born in 1985.He is a Ph.D.candidate at Northeastern University.His research interests include data mining and graph data analysis,etc.

王章辉（1985—），男，河南新乡人，东北大学博士研究生，主要研究领域为数据挖掘，图数据分析等。

ZHAO Yuhai was born in 1975.He is an associate professor at School of Computer Science and Engineering,Northeastern University,and the senior member of CCF.His research interests include data mining and bioinformatics,etc.

赵宇海（1975—），男，浙江舟山人，东北大学计算机科学与工程学院副教授，CCF高级会员，主要研究领域为数据挖掘，生物信息等。

WANG Guoren was born in 1966.He is a professor at School of Computer Science and Engineering,Northeastern University,and the senior member of CCF.His research interests include XML data management,massive data management,high-dimensional indexing and uncertain data management,etc.

王国仁（1966—），男，辽宁沈阳人，东北大学计算机科学与工程学院教授、博士生导师，CCF高级会员，主要研究领域为XML数据管理，海量数据管理，高维索引，不确定数据管理等。

LI Yuan was born in 1986.He is a Ph.D.candidate at Northeastern University.His research interests include data mining and bioinformatics,etc.

李源（1986—），男，辽宁沈阳人，东北大学博士研究生，主要研究领域为数据挖掘，生物信息等。

Top-K Discriminative Subgraph Mining Based on Diversity Measure*

WANG Zhanghui,ZHAO Yuhai+,WANG Guoren,LI Yuan
School of Computer Science and Engineering,Northeastern University,Shenyang 110819,China

Discriminative subgraph can be used to characterize complex graph structures and construct efficient graph classification model.This paper proposes the Top-K discriminative subgraph mining problem based on diversity measure.The diversity measure can be used to mine low correlation subgraph patterns in the mining result,which can enhance the usefulness of the discriminative subgraph patterns.By exploiting the graph structure similarity and support set similarity restraints,this paper introduces the criterion of graph pattern diversity measure.Then this paper proposes two efficient algorithms,Greedy-TopK and Leap-TopK,for the problem.Greedy-TopK algorithm employs two step strategies to incrementally and greedily mine K discriminative subgraphs.By limiting the structure similarity graph pattern extension in the discriminative subgraph mining process,Leap-TopK algorithm can leap the graph pattern searching space.Extensive experimental results demonstrate that Leap-TopK algorithm is more efficient than Greedy-TopK algorithm.Besides,when the mining results of discriminative subgraphs are considered,the classification accuracies of the two algorithms are almost the same.But they are all superior to the traditional discriminative subgraph mining algorithm in terms of usefulness.

graph mining;graph classification;subgraph pattern;discriminative subgraph;diversity

2016-07, Accepted 2017-03.

A

TP311

+Corresponding author:E-mail:zhaoyuhai@ise.neu.edu.cn

WANG Zhanghui,ZHAO Yuhai,WANG Guoren,et al.Top-K discriminative subgraph mining based on diversity measure.Journal of Frontiers of Computer Science and Technology,2017,11(9)：1379-1388.

10.3778/j.issn.1673-9418.1607016

*The National Natural Science Foundation of China under Grant Nos.61272182,61332014,61173029(国家自然科学基金);the Key Program of National Natural Science of China under Grant No.U1401256(国家自然科学重点项目);the Fundamental Research Funds for the Central Universities of China under Grant No.N150402002(中央高校基本科研业务费专项资金).

CNKI网络优先出版: 2017-03-07, http://kns.cnki.net/kcms/detail/11.5602.TP.20170307.1405.008.html

摘 要：区分子图可以用来描述复杂的图数据结构和构建高效的图分类模型。提出了多样性度量的Top-K区分子图挖掘问题，避免了挖掘结果之间出现高度相关的子图模式，提高了区分子图模式的可用性。通过组合图结构相似性与支持集相似性约束，给出图模式的多样性度量标准。提出两个高效算法Greedy-TopK和Leap-TopK挖掘多样性度量的Top-K区分子图。Greedy-TopK算法采用两阶段的增量式贪婪方法快速挖掘K个区分子图模式。Leap-TopK算法通过在挖掘过程中限制扩展结构相似的图模式，实现了跳跃搜索子图模式空间。实验结果表明，Leap-TopK算法的效率明显优于Greedy-TopK算法；在可用性方面，利用Leap-TopK算法与Greedy-TopK算法挖掘结果构建的图分类器具有相似的分类精度，且都优于传统区分子图挖掘算法产生的结果。