基于两级充电管理系统的电动汽车智能充电控制系统研究

2017-09-17韩华春原增泉

电力工程技术 2017年5期

关键词：充电站时段电动汽车

张军, 韩华春, 原增泉

(1. 中国建筑第八工程局有限公司, 北京 100190；2. 国网江苏省电力公司电力科学研究院，江苏南京 211103；3.中国科学院电工研究所，北京 100190)

基于两级充电管理系统的电动汽车智能充电控制系统研究

张军1, 韩华春2, 原增泉3

(1. 中国建筑第八工程局有限公司, 北京 100190；2. 国网江苏省电力公司电力科学研究院，江苏南京 211103；3.中国科学院电工研究所，北京 100190)

随着电动汽车的发展，电动汽车大规模的无序充电将对现有电网的稳定性造成潜在威胁。如果仅以现有电网扩容作为解决方法，不仅需要大量的投资，且在低负荷时会造成容量的浪费。文中提出了一种基于两级电动汽车充电管理系统(electric vehicles charging management system, EVCMS)的优化算法，在满足充电需求的前提下，通过合理调配充电时段和充电速率，来优化需求侧管理，减少电动汽车充电对电网的冲击。该优化算法的影响因素主要包括实时电价、电池剩余容量、电网侧负荷容量和充电时段等。

电动汽车；EVCMS；充电终端；模糊控制

0 引言

电动汽车(electrical vehicles, EVs)以电池作为能源，具有节能、零污染和零排放等优势，正越来越受到各国的广泛关注。但是，随着EVs的普及，大量和无序的充电形成的瞬时大负荷将对电网造成巨大冲击，如电网频率和电网电压的波动，进而对电网的稳定运行形成威胁。此外，EVs的无序接入，还会拉大峰谷差，增加峰时的传输损耗，甚至可能过载，严重损害电网的稳定运行[1-5]。目前，许多学者都在关注这个问题。在文献[6]中，作者研究了整个美国电网对EVs充电的接纳程度，包括12 h和24 h两种可充电场景。结果表明，现有电网容量可以最多容纳EVs负荷需求的73%。在文献[7]中，根据目前丹麦电力市场的价格，作者优化了充电时间和充电量，并得出结论，在有序充电模式下充电成本可以降低到63%。文献[7]也指出，相对于无序充电模式，有序充电可以在不同程度上减小峰值负荷和分布损耗。

文中提出了一种协调有序充电的优化算法，该优化算法是基于所提出的电动车辆充电管理系统(electric vehicles charging management system, EVCMS)来实现的。作为该系统的基本单元，充电终端(charge terminals, CTs)起承上启下的关键作用，一方面通过CAN总线与EVs通信，获取电池荷电状态(state of charge,SOC)和通过输入信息获取用户预计驻留时间，另一方面也负责执行有序充电算法的控制命令。监控主机(monitor host, MH)借助CTs上传的实时信息，运行基于模糊控制有序充电优化算法，来决定充电的启停时刻和充电速率，以实现对电网的削峰填谷的目的。

1 系统结构

随着EVs的大量普及，现有的充电管理系统已不能满足电网新的控制和调度要求。因此迫切需要新的智能控制充电管理系统，来实现实时控制和需求侧管理的功能[8]。

1.1 两级充电管理系统的网络拓朴

文中提出的两级充电管理系统的拓朴结构如图1所示，主要由区域电力调度网络和局域充电控制网络两部分组成。

图1 EVCMS网络结构图Fig.1 Schematic structure for EVCMS network

1.1.1 区域功率调度网络

第一级网络由功率分配中心(power dispatch center, PDC)和各个局域充电网络的MH组成。其中，PDC由电力调度主机承担，为每个局域充电站提供可用最大功率，及时获取每个局域充电站的实时信息，以对每个局域充电站的最大使用功率进行合理、及时地更新。

1.1.2 局域充电控制网络

第二级网络称为局域充电控制网络，是每个充电站内设备互联控制网络。适用于集中充电区域，如公司和住宅区的停车场等。它包括EVs充电、计量和计费、安全、设备管理和其他方面。本文提出的网络是基于SCADA定义[9]设计，由数据采集、设备控制、参数调整、多种报警信号等功能组成。以此可以实现网络交互和控制功能，智能充电控制和实时状态监控功能。

1.2 主要设备

EVCMS由以下设备组成：CTs、充电协调器和MH等。

CTs是整个充电管理系统的基本元素，一方面获取信息和数据，并上传到MH，进行计算和控制指令推理；另一方面，CTs也是MH控制命令的执行者。用户通过人机界面输入预期停车充电时间后，而CTs通过CAN总线与电池管理系统通信获取剩余电池容量、预计充电时间等信息，并以ZigBee[10]无线通信方式上传给MH。

充电协调器是ZigBee无线网络的协调者，负责组织节点、分配终端地址、管理无线子网，以保证CTs和MH之间信息交互的畅达。

MH是有序充电优化算法的执行者，通过获取电力分配中心和CTs的数据和信息，进行智能推理和计算以产生控制指令，并下发给CTs。

1.3 数据传输

图2表明了用户侧、EVs充电管理侧和PDC侧之间的数据和信息流内容以及方向。

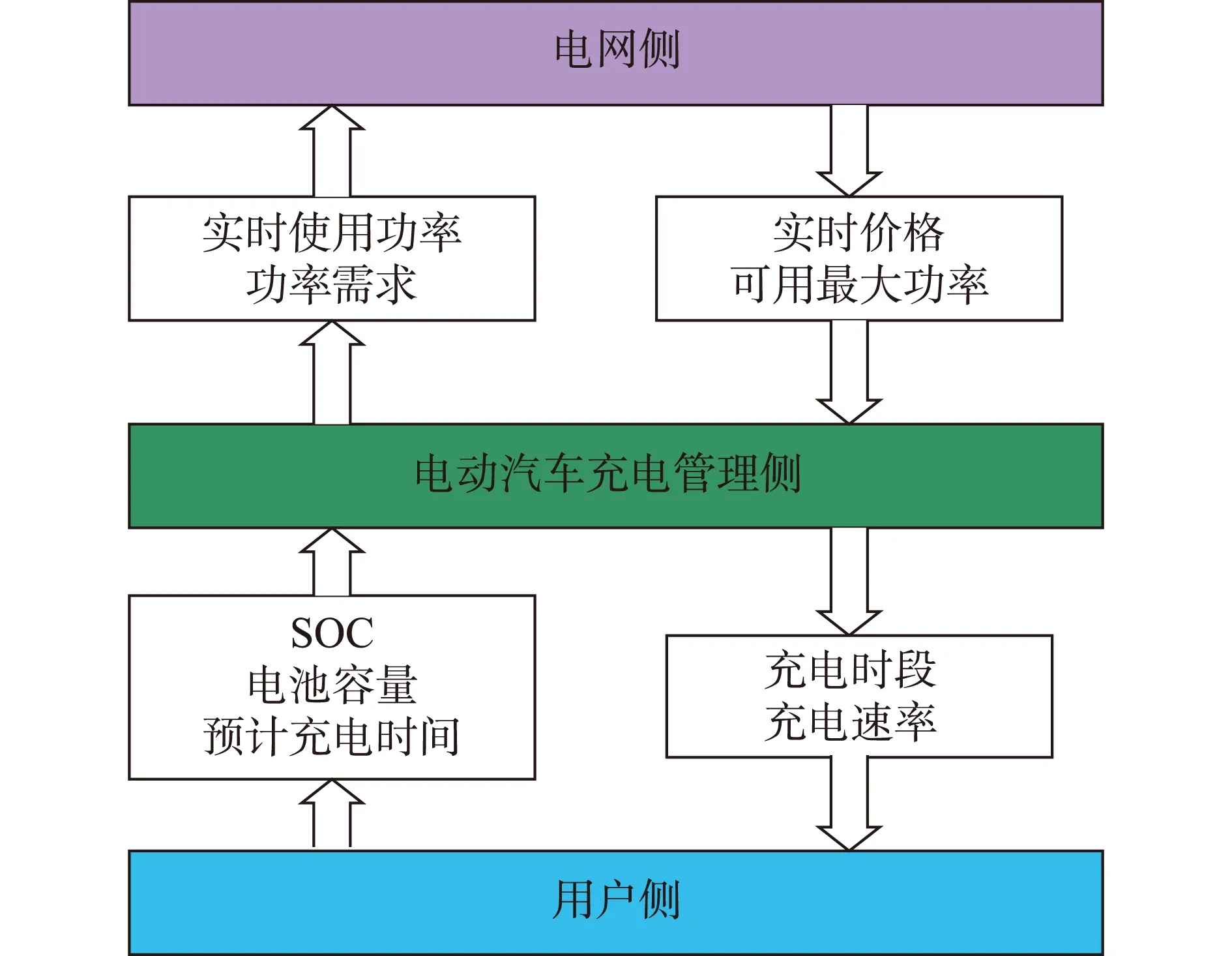
图2 信息传输框图Fig. 2 Schematic for data transmission

用户侧上传EVs充电状态和用户预期停车充电时间。充电状态包括电池剩余SOC、电池总容量、电池类型等。

用户侧信息包括EVs状态和用户的充电期望。EVs状态主要表现为电池SOC、电池容量、最高充电电压、最大充电电流等。用户充电期望包括用户预计停车时间、期望最高和最低电池SOC等信息。EVCMS根据这些信息的实时更新来动态调整控制策略。

EVCMS侧实时接收PDC下传的最大可用功率和电价信息，并上传实时的功率需求信息。

2 充电终端-信息获取和充电控制

CTs是智能充电控制的信息来源和指令执行者。其中，电池的SOC是借助CAN总线与电池管理系统通信获得，而用户期望来源于充电设置时的用户输入。此外，PDC的电价信息和EVCMS下发的控制指令通过CTs来存储和执行。交流CTs通过PWM信号控制最大充电电流，直流CTs通过DC-DC控制充电电压和充电电流，通过对启停和充电功率控制，从而实现可以优化站内的充电时间调度和站内总充电功率的控制。

2.1 充电终端CTs

现有的CTs可分为直流充电、交流充电或者两者皆有。以交直流终端为例，交流和直流CTs原理结构框图如图3所示。可分为控制单元、直流功率单元和交流功率单元。

图3 交流和直流CTs结构框图Fig.3 Schematic for charging terminal’s structure

(1) 基本的控制单元包括MCU控制器、LCD触摸屏、刷卡模块、ZigBee通信模块和CAN总线模块。

ZigBee模块使每个CTs成为ZigBee网络的一个节点，并通过充电协调器与MH进行数据交互。CAN总线模块使CTs一方面可以与直流功率单元进行数据交互控制直流功率单元的输出状态，另一方面与EVs的电池管理系统(BMS)通信，接受BMS的充电控制和状态参数。

(2) 直流功率单元用于直流CTs，其将输入的三相380 V交流电压转换为电压和电流可调节的直流电，以用于给电池包充电。直流功率单元主要包括三相VSR、隔离DC-DC和基于DSP的控制单元。其中3个VSR将输入的三相交流电压整流为直流750 V左右的高压作为DC-DC的输入，DC-DC采用移相全桥结构调节输出端的电压和电流大小。同时，在交流三相输入端，采用三相交流电表作为计量单元。

交流功率单元通过控制交流接触器来控制交流供电的通断，同时通过充电插头的连接导引电路控制PWM信号的占空比大小，确定CTs的可用功率，以此限制EVs的最大充电功率。同时，在交流输出线上采用单相交流电表作为计量单元。

2.2 CTs与BMS的CAN总线通信协议

CTs借助CAN总线[11,12]与BMS交互进行充电控制，包括6个阶段：物理连接完成、低压辅助上电、充电握手阶段、充电参数配置阶段、充电阶段和充电结束阶段。在各个阶段，CTs和BMS如果在规定的时间内没有收到对方报文或者正确报文，即判定为超时，同时进入错误处理流程。

3 电动汽车充电优化控制策略

EVs充电优化控制策略运行在监控控制主机上，称为充电控制单元。充电控制单元主要由参数计算模块、模糊推理模块和实时数据采集模块3部分组成。

3.1 参数计算模块

对用户来说，充电行为可以理解为在一定时间内EVs的SOC达到某个期望值。因此对于大规模的EVs充电来说，其充电功率需求和充电时间长度是决定充电速率和充电时段优化调度的2个主要影响因素。

3.1.1 充电需求功率计算

对于直流CTs来说，忽略其本身的功率损耗；对于交流来说，忽略车载CTs的功率损耗，充电功率需求为：

Pmax=VbatIbat=VCTICT

(1)

式(1)中：Vbat为电池包的充电电压；Ibat为电池包的充电电流；VCT为CTs的输出电压；ICT为CTs的输出电流。

3.1.2 充电时间长度计算

充电时间长度是通过预期停驶充电时间、电池SOC、电池容量和充电速率共同决定的。文献[13]中，在EVs整个充电过程中，先以恒流模式充电再以恒压模式充电。其中， 0.3C的恒流充电模式占整个充电时间约96.14% ，而充电电压相差不大，C为电池容量。因此充电时间长度为：

(2)

式(2)中：TP为实际充电时间长度；Tep为预计停驶的可充电时间长度，该参数通过用户输入获得；E为电池的容量，对于不同类型的EVs，该值是不同的；Pvat为式(1)中的实际充电功率；SSOC为电池的剩余容量，以百分比表示，100%表示电池已经充满，不需要充电。

3.1.3 可用最大功率

优化算法的每次优化计算，所得到的站内所有CTs的最大功率输出值都必须小于充电站可用最大充电功率Pgrid，即本站所有CTs的总功率不得超过该值，该值由区域功率调度中心实时下发，即：

(3)

式(3)中：Ptotal为充电站内所有CTs的实际最大输出功率总和；Pmax为每个CTS的最大输出功率。

3.2 模糊推理算法

模糊控制是一种基于规则的控制。它直接采用语言型控制规则，出发点是现场操作人员的控制经验或相关专家的知识，在设计中不需要建立被控对象的精确数学模型，因而使得控制机理和策略易于接受与理解，设计简单，便于应用[14]。

当一个用户在停车场上停车时，如不能准确地输入要停驶多长时间。则用户的停车时间是“长”、“中”和“短”，而不是以秒计的精确时间。因为不同的EVs具有不同电池类型和剩余电池容量，并且不同用户有不同停驶需求，所以难以为大规模充电应用创建精确的数学模型。因此对于此种情况，模糊推理是非常合适的。使用每辆EVs的电池SOC和每个用户期望充电时间2个主要影响因子作为模糊控制器的输入。通过模糊化、模糊推理和解模糊，得出各个EVs充电速率和充电时间和长度。

3.2.1 模糊推理规则

根据实际调节的经验，优化充电控制模糊推理规则如表1所示。例如，剩余电池容量SOC较高意味着只需要一小部分充电电量即可把电池充满；假设其预计停驶时间也比较长，这就意味着该车的充电时间段可以优化到该车离开前的一小段时间内，并且充电速率也不需要太大。这样就避免了该车即插即充，分用站内的充电功率。而当SOC较低，预计停驶时间较短时，则意味着需要立即对EVs进行充电，且充电功率较大，以满足用户的继续驾驶使用需求。

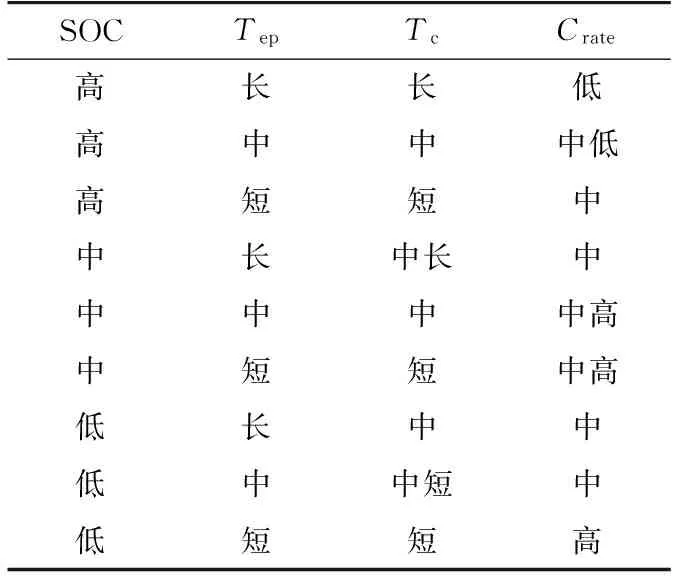
表1 模糊推理表Table 1 Table for fuzzy inference

3.2.2 隶属度函数

隶属度函数的形状在很大程度上影响控制结果，在文中经过综合考虑隶属度函数的性质和计算的简便性，选用三角函数作为隶属度函数的形状。输入变量和输出变量的隶属度函数如图4所示。电池组的SOC小于45%为“低”；在25%～75%为“中”；大于60%则为“高”。同时，为了得到更精度的输出控制量，将输出变量的隶属度函数分为5个类型，“小”、“中小”、“中”、“中大”和“大”。

图4 输入输出变量的隶属度函数Fig.4 Schematic for charging terminal’s structure

3.2.3 推理方法和解模糊

Mamdani推理法是经过多个学者证明和实践过的合理的推理方法[15]，文中的推理方法采用该方法。而解模糊的方法采用重心法，重心法有平滑输出推理机制的特点，更适合文中的解模糊情况[16]。

3.3 控制规则

文中系统控制输出的每次更新前提源于2个触发条件的发生，一个是从PDC发送的最大可用功率的更新，另一个是有EVs接入充电或者充电完成。当这2个条件中的任一条件发生，控制系统将重新计算并更新控制输出且下发给CTs。当有较低或较高SOC的车辆突然接入充电或者充电完成离开时，将会打破上次推断调整的控制结果的平衡。例如，当较低SOC的车辆接入充电时，控制系统需要根据所有车的SOC状态和剩余停车持续时间重新分配每辆EVs的充电时间段及充电速率，并重新下发给CTs进行更新输出。总而言之，调整是动态的和实时的，并且随着充电状态的变化而变化。

4 仿真实验

为了便于分析，文中假设电网功率在EVs充电过程中是恒定值。选取5辆同一型号的EVs，即其电池容量和最大充电功率相同，SOC期望值均为1，即充满电，充电站的总可用功率为35 kW。根据车主的行为习惯，EVs在站内预计停留时长服从均匀分布U(2，6)，初始SOC服从正态分布N(0.4，0.12)，据此随机产生5辆车的充电需求数据，如表2所示。

表2 EVs的充电需求数据Table 2 Charging needs data for EVs

不失一般性，EVs在自主充电行为下，先到先充，车到站后有空位即可接入充电桩，如果此时充电站可用充电功率有剩余，则车按其最大充电功率进行充电；如果功率达不到其最大充电功率，则按充电站剩余可用充电功率进行充电。后到的EVs暂时无可用充电功率，处于等待状态。待有车充完电离开时，等待充电的车按先后顺序连入充电桩进行充电。

图5为先到先充模式下，无序充电时各时段各车充电功率分配结果。

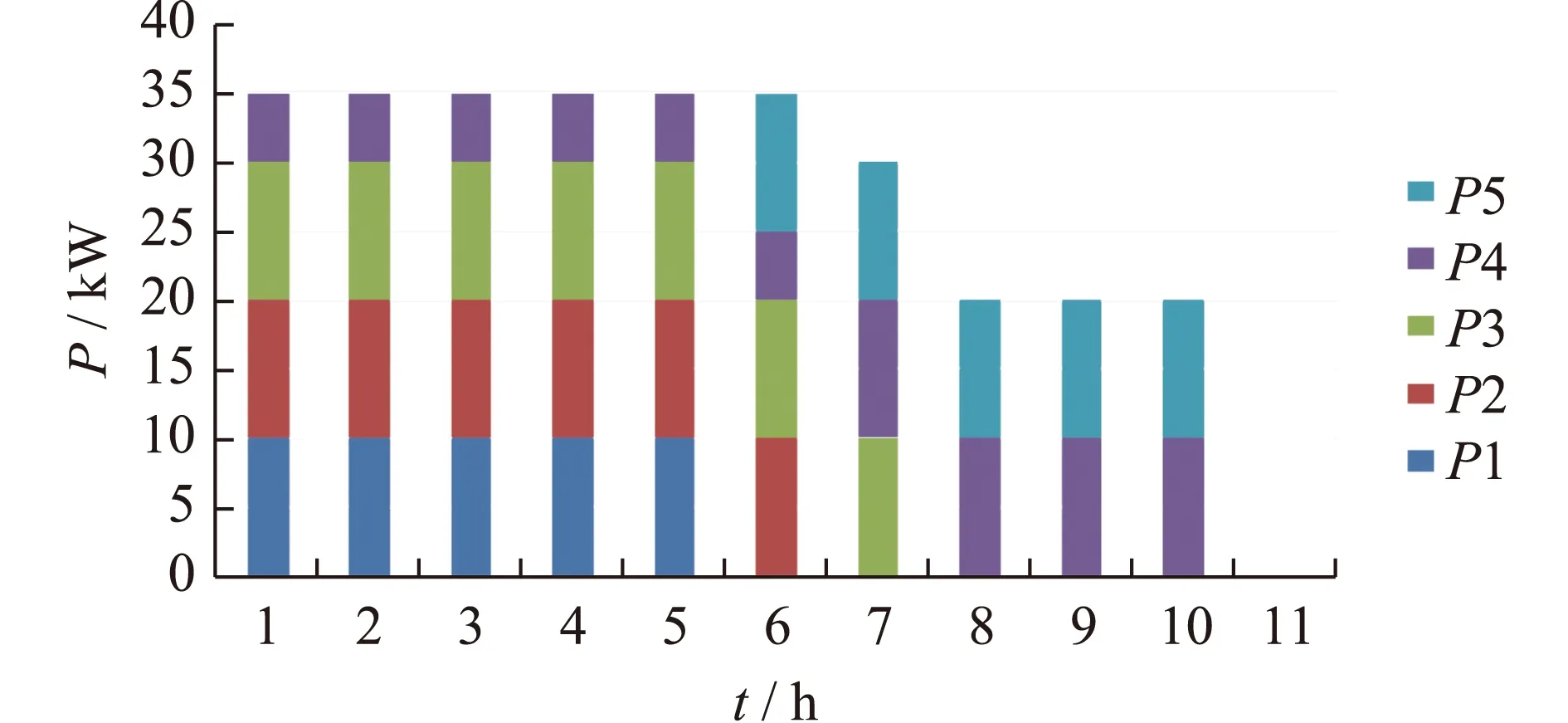
图5 各时段EVs充电功率分配图(无序)Fig.5 Schematic for charging terminal’s structure

由图5可以看出，先到的前3辆车被分配了其最大充电功率10 kW，第四辆车使用站内剩余功率5 kW充电，第五辆车在前5个充电时段内充电功率都为0，即处于等待状态，各时段EVs的SOC值(无序)如图6所示。

图6 各时段EVs的SOC值(无序)Fig.6 Schematic for charging terminal’s structure

从图6可以看出先到的前3辆车以其最大充电功率10 kW进行充电，其SOC值随时间变化的斜率最大；第四辆车以充电站剩余的5 kW功率进行充电，其斜率次之；最后到达的第五辆车没有可用充电功率，处于等待状态，斜率为0。直到第六个控制时段，即75 min后，第一辆车SOC达到1充满离开，第五辆车才连入充电桩开始进行充电。第五辆车充满电时已经在站内停留了10个充电周期，即150 min，超过了其预期停留时间。因此这种基于先到先充的充电方式不能满足用户的充电需求。而与之相对，经过控制优化下的有序充电过程，则可以满足要求。各时段EVs充电功率分配图(有序)如图7所示。

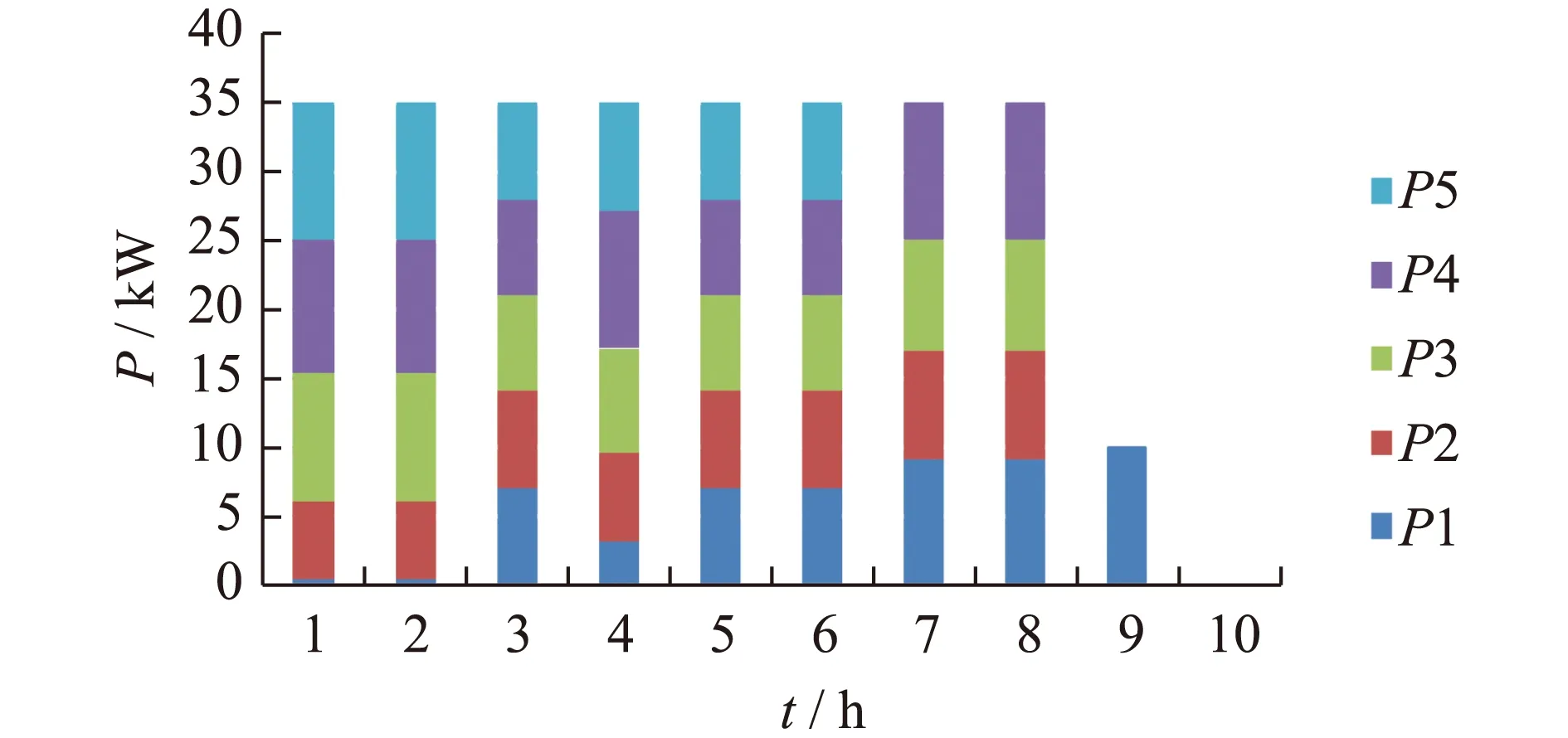
图7 各时段EVs充电功率分配图(有序)Fig.7 Schematic for charging terminal’s structure

由图7可以看出在充电站总可用功率35 kW的约束下，充电需求最紧急的第五辆车在前几个时段就被分配了较大的充电功率，因此在第六个控制时段就完成了充电，充电时长约为6T=90 min，小于其预期停留时间，满足了其充电紧急需求。同时由于第一辆车优先级最低，在前2个控制时段内充电功率几乎为0；到第3个控制时段，其剩余充电时间缩短，待充电电量较大，因此此时其实时优先级较高，因此本时段被分配了较高的充电功率。各时段EVs的SOC值(有序)如图8所示。

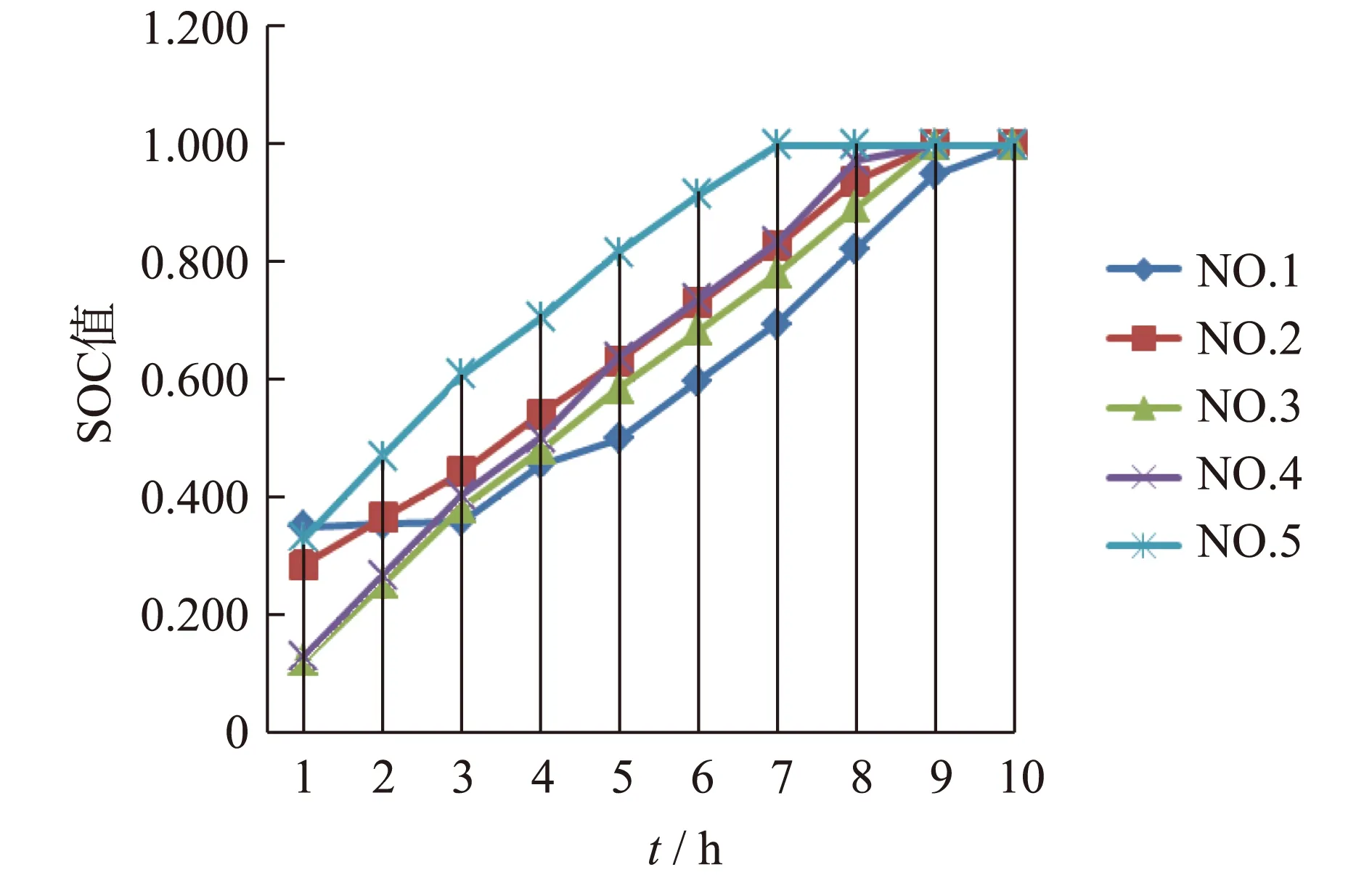
图8 各时段EVs的SOC值(有序)Fig.8 Schematic for charging terminal’s structure

从图8中可以看出第五辆车一直拥有较高的充电优先级，其电池SOC值在5辆车中以较大的斜率增长；在前2个控制时段内，优先级较低的第一辆车SOC值基本没变，优先级较高的2，3，4车的SOC值则以较大的斜率增大；随着时间增长，由于各车剩余充电时间的缩短和已充电电量的不同，各车的优先级不断发生变化，相应地其SOC的增长斜率增大或减小。各车均满足了在指定充电时间内达到期望SOC。

在总功率限制的情况下，有序充电将时间充裕且电量需求较小的第一辆车延迟了30 min，而对充电需求最紧急、停留时间最短的第五辆车给予较大的充电功率，使其在所有车中最先完成充电，满足了其优先级。对于其余车，有序充电控制程序根据其各自的实时电池SOC状态和剩余可用充电时间在每一控制时段对其充电功率进行调整，最终所有车充电完成所花费的时间均满足其预期。

5 结论

文中提出了适用于大规模电动汽车充电应用的两级充电管理系统结构。该系统不仅适用于分布式充电控制，还适用于集中充电的有序控制。最主要的是结合了这2个方面，能够真正减轻大量电动汽车负载变化对电网的影响。同时，本系统可以使用有线通信和无线通信2种通信方式，可以使系统状态的采集和控制命令的传达更为有效和及时。

另外，在本系统中，电动汽车电池的SOC、停车充电的时间都是模糊控制逻辑的主要影响因素。同时，模糊推理和计算是实时的，并根据触发条件进行更新。由于充电过程的随机性和不确定性，很难建立精确的数学模型并根据模型进行控制，而模糊控制不需要精确数学模型，在该应用场合特别适合。仿真实验证明该控制方法可以有效地解决电动汽车负载的调度控制，减小大规模充电对电网的影响。

[1] MOHSENI P, STEVIE R G. Electric vehicles: Holy grail or fool’s gold[C]∥Power & Energy Society General Meeting, Minnesota, USA, 2009: 1-5.

[2] PILLAI J R, BAK-JENSEN B. Impacts of electric vehicle loads on power distribution systems[C]∥Vehicle Power and Propulsion Conference, Lille, North France, 2010: 1-6.

[3] PARRY E, REDFERN M. Load management of the electricity supply network using plug-in vehicles[C]∥Universities Power Engineering Conference, Cardiff, UK, 2010: 1-6.

[4] SHAHIDINEJAD S, FILIZADEH S, BIBEAU E. Profile of charging load on the grid due to plug-in vehicles[J]. IEEE Transactions on Smart Grid, 2012, 03(1): 135-141.

[5] TREMBLAY O, DESSAINT L A, DEKKICHE A I. A generic battery model for the dynamic simulation of hybrid electric vehicles[C]∥Vehicle Power and Propulsion Conference, IEEE, 2007: 284-289.

[6] CLEMENT-NYNS K, HAESEN E, DRIESEN J. The impact of charging plug-in hybrid electric vehicles on a residential distribution grid[J]. IEEE Transactions on Power Systems, 2010, 25(1): 371-380.

[7] SCHNEIDER K, GERKENSMEYER C, KINTNER-MEYER M, et al.Impact assessment of plug-in hybrid vehicles on pacific northwest distribution systems[C]∥Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century. IEEE, 2008: 1-6.

[8] HU W, CHEN Z, BAK-JENSEN B. Optimal operation of electric vehicles in competitive electricity markets and its impact on distribution power systems[C]∥ IEEE PES Powertech, Trondheim, Norway, 2011: 1-7.

[9] BRUCE A G. Reliability analysis of electric utility SCADA systems[C]∥IEEE Power Industry Computer Applications Conference, Columbus, Ohio, 1997: 200-205.

[10] KIM S H, KANG J S, PARK H S, et al. UPnP-ZigBee internetworking architecture mirroring a multi-hop ZigBee network topology[J]. IEEE Transactions on Consumer Electronics, 2009, 55(3).

[11] WAN Xiaofeng, XING Yisi, CAI Lixiang. Application and implementation of CAN bus technology in industry real-time data communication[C]∥ IEEE Industrial Mechatronics and Automation Conference, Changchun, China, 2009: 278-281.

[12] LI Ran, WU Junfeng, WANG Haiying, et al. Design method of CAN BUS network communication structure for electric vehicle[C]∥Strategic Technology, Ulsan, South Korea, 2010: 326-329.

[13] TREMBLAY O, DESSAINT L A, DEKKICHE A I. A generic battery model for the dynamic simulation of hybrid electric vehicles[C]∥ IEEE Vehicle Power and Propulsion Conference, Texas, USA, 2007: 284-289.

[14] LEE C C. Fuzzy logic in control systems: fuzzy logic controller. [J]. IEEE Transactions on Systems, Man, and Cybernetics, 1990, 20(2): 404-418.

[15] MENDEL J M. Fuzzy logic systems for engineering: a tutorial[J]. Proceedings of the IEEE, 1995, 83(3): 345-377.

[16] TEIXEIRA M C M, ZAK S H. Stabilizing controller design for uncertain nonlinear systems using fuzzy Models[J]. IEEE Transactions on Fuzzy Systems, 1999,07(2): 133-142.

(编辑徐林菊)

Smart Charging Control Electrical VehiclesBased on Two-level Charge Management System

ZHANG Jun1, HAN Huachun2, YUAN Zengquan3

(1. China Construction Eighth Engineering Division Co., Ltd, Beijing 100190, China;2. State Grid Jiangsu Electric Power Company Research Institute, Nanjing 211103, China;3. Institute of Electrical Engineering CAS, Beijing 100190, China)

The application of large-scale eectric vehicles (EVs) poses a threat to grid stability if charged without control. It needs expansion of the grid capacity and leads to major investment in current grid and capacity-wasting in low-load time. This paper proposes a solution based on two-level electric vehicles charging management system (EVCMS) to optimal demand side management by means of scheduling charging time and setting charging rates. The influence factors for power management include electricity prices, state-of-charge (SOC) of the battery, electricity available, park duration and others. All these can be achieved through charge terminals (CTs)

electric vehicle; EVCMS; CTs; fuzzy inference