计及户用分布式电源的合作博弈智能用电技术

2017-09-17陈彬

电力工程技术 2017年5期

关键词：电力公司时段分布式

陈彬

(国网福建省电力有限公司电力科学研究院，福建福州 350007)

计及户用分布式电源的合作博弈智能用电技术

陈彬

(国网福建省电力有限公司电力科学研究院，福建福州 350007)

在智能电网环境下，参与需求侧管理的居民用户可以根据发布的实时电价进行合适的家庭负荷用电安排。文中考虑分布式电源作为居民用户电力自发自用的一种方式，提出基于合作博弈的居民用户智能用电技术。在建立用户电力消耗模型、用电成本模型和负荷控制模型的基础上，将需求侧居民智能用电技术描述为一个合作博弈模型，模型中以多个用户作为博弈参与者，以用户的日负荷用电安排作为参与者的策略。该合作博弈模型在纳什均衡解处，各用户的能源消费最小。算例仿真结果表明，用户参与合作博弈的负荷用电安排可有效降低其电费，且当用户配有分布式电源时，电费将进一步降低。

需求侧管理; 合作博弈; 能源消耗调度; 户用分布式电源

0 引言

为了解决化石能源逐渐枯竭、环境污染日益严重的问题，同时为了满足负荷增长需求以及更有效地利用能源，以太阳能、风能等可再生清洁能源发电的分布式发电技术应运而生[1,2]。为了充分发挥分布式电源在电网中的作用，智能电网终端智能配用电侧广泛考虑了需求侧管理(demand side management, DSM)技术[3]。DSM是指在政府法规和政策的支持下，采取有效的激励和引导措施，改善居民用户用电方式，在满足同样用电功能的同时减少电量消耗和电力需求，提高终端用电效率[4,5]。它可以降低负荷曲线的峰均比，平衡电力供需以及减少用户的电力成本。智能电网下的DSM具有更高的负荷监控技术、智能控制技术和终端节能效率，能实现实时的用户响应，并且支持分布式电源的自由接入。

为了实现DSM调节作用，往往采用智能电价机制，包括尖峰电价、分时电价和实时定价[6,7]。电力公司通过给予用户一定的电价激励机制，鼓励用户安排其负荷从用电高峰时段向低谷时段转移，这样不仅减少用户的电费，而且能够缓解电网的压力。此外，智能电表和智能家电是居民家庭智能用电系统的重要组成部分[8]，智能电表的引入以及双向通信的实现是智能电网进行负荷用电安排的主要技术驱动，也为电力公司和居民用户等利益主体进行优化博弈决策提供了可能[9]。

迄今为止，国内外已有不少学者对博弈论用于解决智能电网中负荷用电安排问题进行了研究并取得重要进展。文献[10]研究了电力公司实施的分时电价政策，提出了成本函数模型，并描述了一种基于博弈论的方法，优化分时定价策略。文献[11]针对电力公司和终端用户之间的信息交互建立了斯坦克尔伯格博弈模型，电力公司作为博弈中的主导者，而用户作为跟随者。文献[12]考虑了多个电力公司和多个用户之间的相互关系，建立了一个双层博弈模型，其中将电力公司之间的竞争阐述为非合作博弈，把用户之间的交互阐述为演化博弈。文献[13-15]研究了利用贝叶斯博弈解决信息不完全情况下的DSM问题。文献[13]针对用户不能及时知道其他用户用电信息的情况，通过建立贝叶斯博弈模型优化用户用电策略。文献[14]研究了信息传递过程中信息缺失时用户和电力公司之间的博弈行为。然而上述文献都没有把分布式电源考虑到博弈模型中，并未对家庭含有分布式电源情况下用户用电行为的博弈模型作过详细讨论。

文中在智能电网环境下，考虑了户用分布式电源存在情况下，居民用户可用其发出的电能供负荷使用，并可将剩余电能回售给电网。在分时电价的基础上，配有智能电表的各用户参与能源消耗调度(energy consumption schedule, ECS)，适当安排可转移负荷的使用时段以降低电费。基于上述分析，文中基于合作博弈思想建立了居民用户关于负荷智能用电的优化模型，通过利用该模型对用户的日负荷进行优化安排，在该模型中居民用户为博弈参与者，用户的日负荷用电安排为博弈策略，博弈的目标是使得用户的能源消耗费用最小。仿真结果表明，当用户参与ECS时其电费大大减少，且当部分用户配有分布式电源以自发自用时，这些用户的电费将进一步降低。

1 系统建模

以微网作为研究对象进行建模，如图1所示，该微网中有N个居民用户和1个电力公司，其中电力公司主要负责信息收集和负荷调度，而N个居民用户则以相互合作的关系共同参与需求响应。用户家庭负荷包括可转移负荷和不可转移负荷，所有用户均装设智能电表。部分居民用户家中安装有分布式电源(光伏电源)，这些用户可以通过从电力公司购电满足家庭负荷需求，也可以通过光伏电源发电满足家庭电力需求，并且可将光伏多余电量回售给电网。另外，电力公司制定、发布合适的电价并售电给用户，通过电价激励机制促使用户适当地安排家庭可转移负荷的使用。用户与电力公司通过信息网络线进行电价信息和负荷需求的交互，从而完成合作博弈达到优化目的。

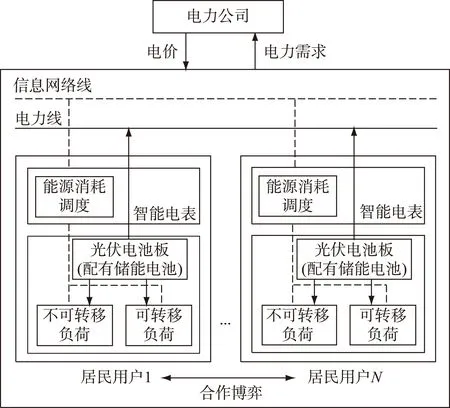
图1 微网需求侧管理场景Fig.1 DSM scenario of micro-grid

1.1 电力消耗模型

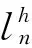
(1)

根据用户日峰荷和平均负荷可计算出需求侧负荷的峰值与平均值的比值PAR为[16]：

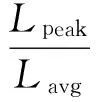
(2)

其中，Lpeak表示一天内负荷最大值；Lavg表示一天内负荷平均值。

1.2 电能成本模型

为了促使用户合理的消费电力资源，需定义具有激励性质的用户电价。定义Ch(Lh)为电力成本函数的基本形式，其包含了每小时的发电或配电成本，因而直接反映了发电厂的能源成本或用户在第h∈H小时内消耗电能对应的成本。对于上述成本函数，需满足如下条件。

(1) 成本函数关于h∈H时刻总的负荷耗电量是单调递增的，即：

(3)

(2) 成本函数是严格凸函数，即对于任意的0<θ<1，都有：

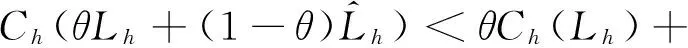
(4)

(3) 当居民用户向电力公司购电时，有Lh>0且Ch(Lh)>0；当居民用户利用光伏电池板发电有多余电量回售时，对于Lh<0的部分，有Ch(Lh)<0。

基于上述3个条件，可选择如下二次函数形式作为成本函数：

(5)

其中，ah>0，bh≥0，且ah和bh都为固定的参数。

1.3 家庭负荷控制

对于用户n，用An来表示其家庭所有负荷集合，其中包括冰箱、照明、洗衣机等。对于装有分布式电源的居民用户而言，其负荷既可以使用从电网购得的电能，也可以使用光伏电池板发出的电能。对于该类用户任一负荷a∈An，定义其消耗从电网购得的外部电量的调度向量为：

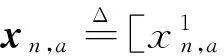
(6)

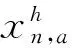
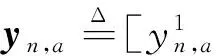
(7)

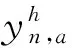
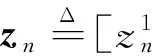
(8)

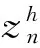
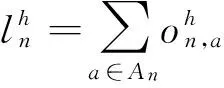
(9)

根据图1所示，用户负荷分为不可转移负荷和可转移负荷。假定所有负荷一天总用电量保持不变，对于不可转移负荷来说，它们只能固定在一定的时间段内使用，因此在用户参与ECS时，只需系统地管理可转移负荷的电力消耗时段即可。但无论是不可转移负荷或可转移负荷，其电力消耗都满足下式：

(10)

其中，αn,a为用户n的负荷a工作起始时刻，βn,a为负荷a工作结束时刻，αn,a<βn,a;Ηn,a为负荷a的工作时段;En,a为用户n的负荷a在工作时段内的耗电量。当负荷a为不可转移负荷时，则αn,a=1，βn,a=24。从而，所有用户一天内全部负荷总的用电量为：

(11)

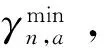
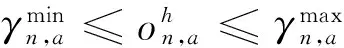
(12)

引入变量向量on来表示用户n的所有负荷An的用电安排on,a。因此，对于用户n来说，其可行的能源消耗调度集On表示如下：

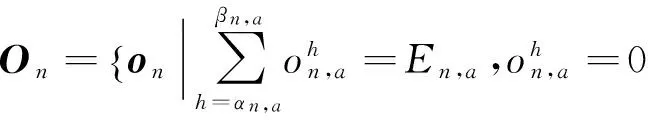
(13)

2 基于合作博弈的能源消耗调度

根据设定的电价，每个用户将根据智能电表之间的信息交流调整其负荷的能源消耗，以降低能量消耗成本。本节基于合作博弈论的方法给出一种按照用户实际用电需求的能源消耗调度。

2.1 能源成本最小化

对于居民用户而言，参与能源消耗调度的目的是减少消耗的能源成本。要找到一种高效的能源消耗调度，使得所有用户的能源成本最小化，因此可以描述成以下的最优问题：

(2) FEP与外部时钟系统采用自开发软件。由于Meinberg工具对于上层时钟源在1 000 s之内发生的偏差或跳变,下一层时钟均可以与上层同步;而实际信号系统一般规定外部时钟源存在几秒或十几秒的偏差或跳变时，停止信号系统通信前置机与外部时钟系统同步。

(14)

根据前文假设，成本函数Ch是严格凸函数，所以式(14)属于严格凸优化问题，可以用凸函数的规划方法求解，比如内点法[15]。

2.2 电力消耗费用

假设bn表示用户n一天所需支付的电力消耗费用，则所有用户总电费为：

(15)

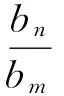
(16)

进一步有：

(17)

由此，用户n的电费计算得：

(18)

其中，

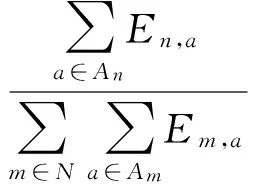
(19)

Ωn表示用户n消耗的电量相对于所有用户所消耗的总电量的比例。上式说明：在智能需求侧管理中，当各用户之间以合作模式进行博弈时，每个用户支付的电费不仅取决于该用户自身的用电量，也与其他用户的用电量有关。

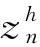
(20)

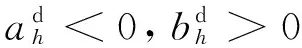
(21)

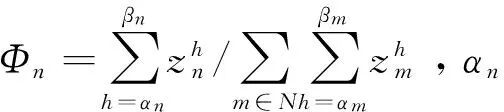
(22)

2.3 博弈模型

居民用户之间的智能用电博弈模型建立如下：

(1) 博弈参与者,集合N中所有的居民用户；

(2) 策略空间,居民用户的负荷用电安排；

(3) 收益函数,用户n的收益函数Pn(on;o-n)定义为：

Pn(on;o-n)=-bn

(23)

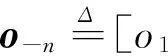
基于上述博弈模型中策略和收益函数的定义，所有用户将参与负荷调度以减少电费支出，直到该博弈达到纳什均衡点：

(24)

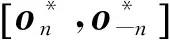
3 算例仿真

算例中，考虑包含1个电力公司和50个居民用户的小型智能电网系统，并且每个用户都愿意参与ECS。假设系统中用户有不可转移负荷(冰箱、照明等)和可转移负荷(洗衣机、电动汽车等)。由于每个用户家中不可转移负荷的类型和数目各不相同，因此假设每个用户不可转移负荷总量在一定范围内波动，如图2所示：每个用户不可转移负荷总量在上下限内随机产生，随机函数形式为xu-(xu-xl)×rand(1)，其中xu和xl分别为用户不可转移负荷总量的上下限，rand(1)表示在[0,1]间随机产生一个数。另外，假设用户均装有小型光伏电池板，既可以将发出的电能直接供负荷用，又可以将多余的电能反售给电网，光伏电池板工作时段为6∶00—17∶00，其光伏典型出力根据文献[17]中预测数据所得。

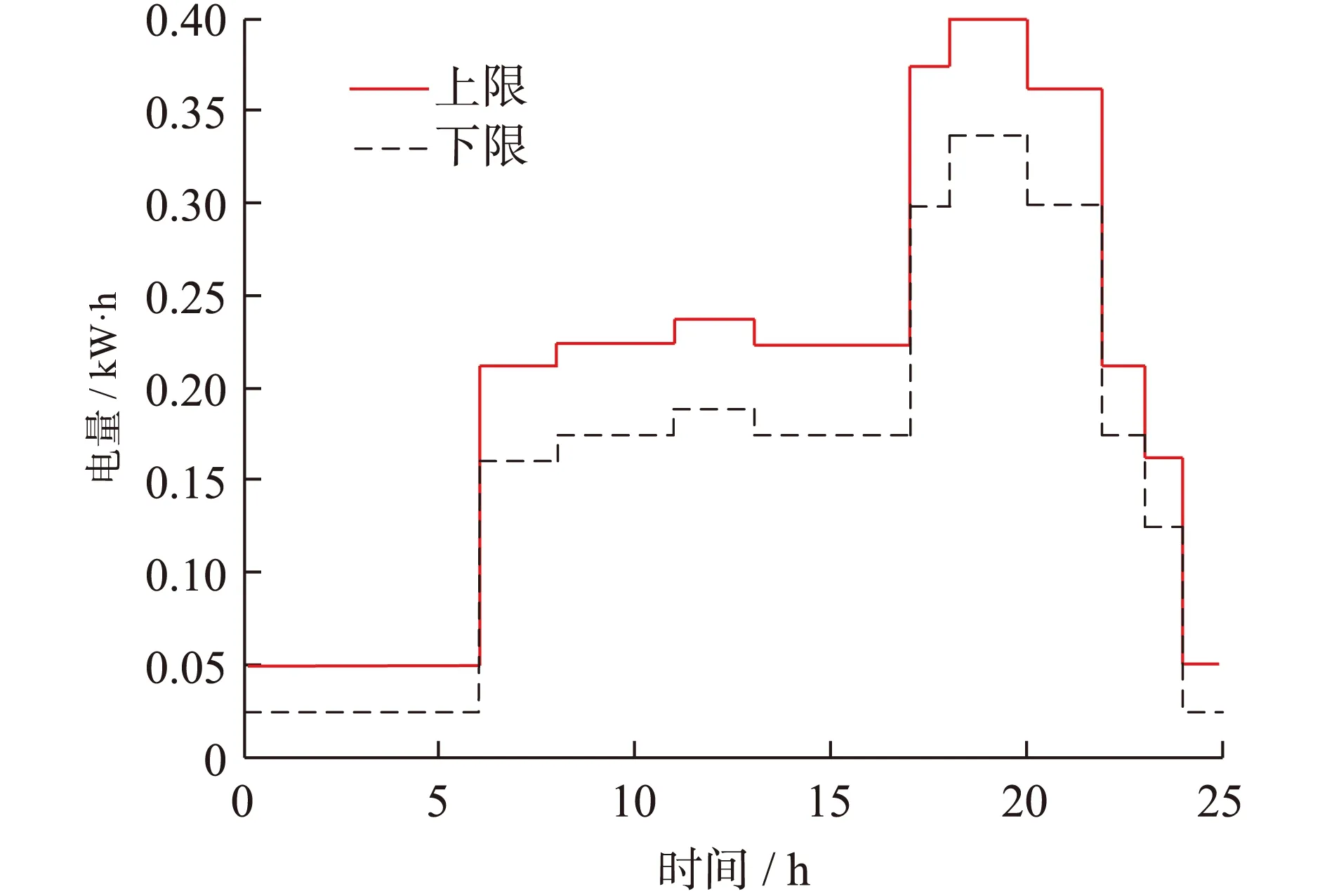
图2 用户不可转移负荷Fig.2 un-shiftable loads of users

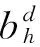
图3为50个用户参与ECS后总费用随着迭代次数增加的变化趋势，经过50次迭代后费用稳定在629.5元，从而用户总费用从未优化前的708.0元逐渐降至629.5元。

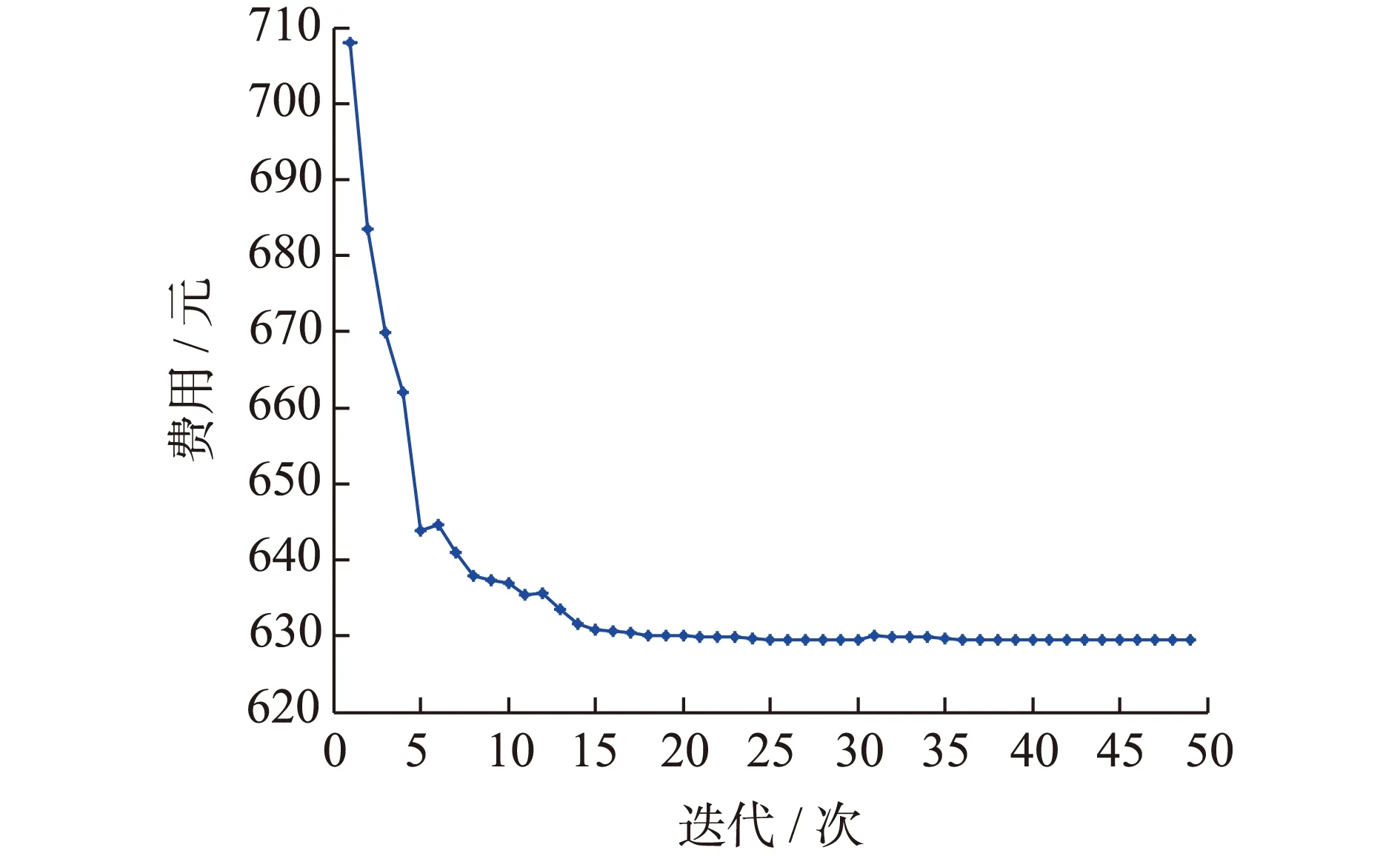
图3 用户总费用收敛趋势Fig.3 Convergence trend of users’ total cost

图4为用户参与ECS前后总负荷的分布情况，其中负值表示用户反向卖给电网的电量。用户未参与优化时，用户负荷基本集中在17∶00—24∶00时段，而0∶00—6∶00负荷较少。用户参与优化后，可以在时段6∶00—17∶00工作的可转移负荷基本上都集中在10∶00—14∶00进行工作，因为该时段光伏出力达到峰值，用户可以最大限度的使用其所发电能；可以在时段17∶00—24∶00和0∶00—6∶00工作的可转移负荷基本上都集中在0∶00—6∶00进行工作，因为该时段处于用电低谷，电价较其他时段便宜。用户在参与优化时通过光伏向电网所售电量明显高于用户未参与优化的售电量。另外，根据PAR计算可知，在未参与ECS时，PAR为2.48，而参与ECS时，PAR为2.10。因此，用户参与ECS不仅能够降低用户的用电费用还可以降低系统的PAR，从而有利于电力网络系统的稳定运行。

用户负荷经过优化后，可以得到各用户可转移负荷的具体用电时段，本文以用户1的负荷安排为例，详见表1。其中，数字1表示负荷处于开通状态，数字0表示负荷处于关闭状态。图4为用户参与ECS前后每小时负荷的分布情况，其中负值表示用户反向售电给电网。对应于图4用户的时用电量，图5为所有用户的时用电费用。从图中可以看出用户在峰时段费用最高，而在时段10∶00—15∶00由于光伏发电量满足家用负荷后仍存在剩余电量，从而通过售电获得一定的收益。50个用户每天的用电费用如图6所示，从图5中可以看出用户未参与ECS优化前的平均费用约为14.26元，而参与优化后平均费用约为12.59元，因此用户人均费用降低约12%。

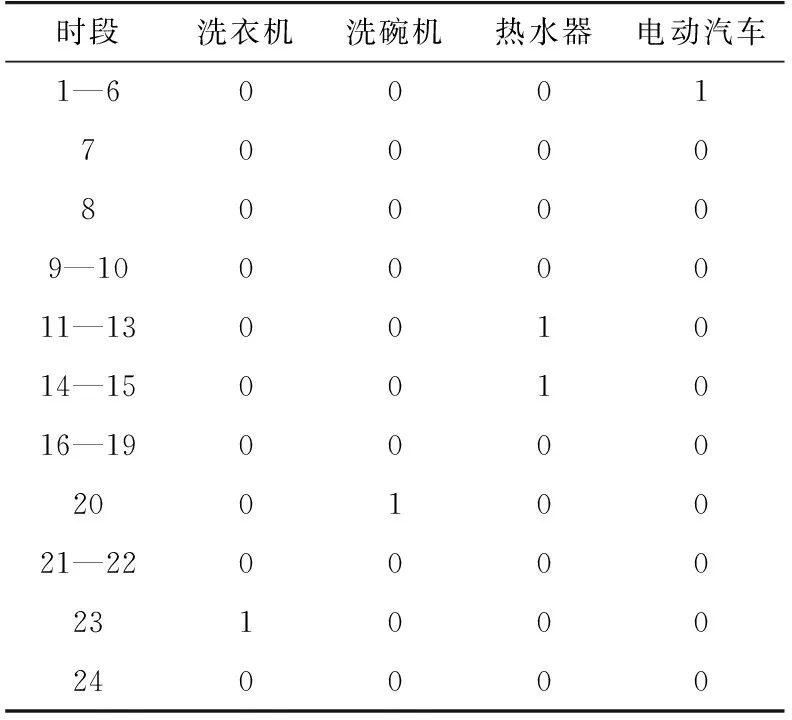
表1 用户1的负荷安排Table 1 Energy consumption schedule of user 1

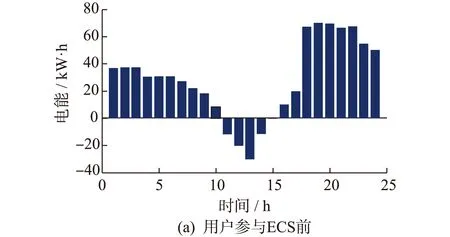
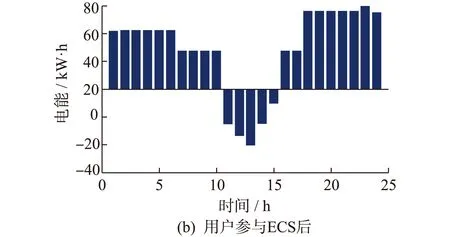
图4 用户参与ECS前后每小时总负荷量Fig.4 Users’ energy consumption without/with ECS

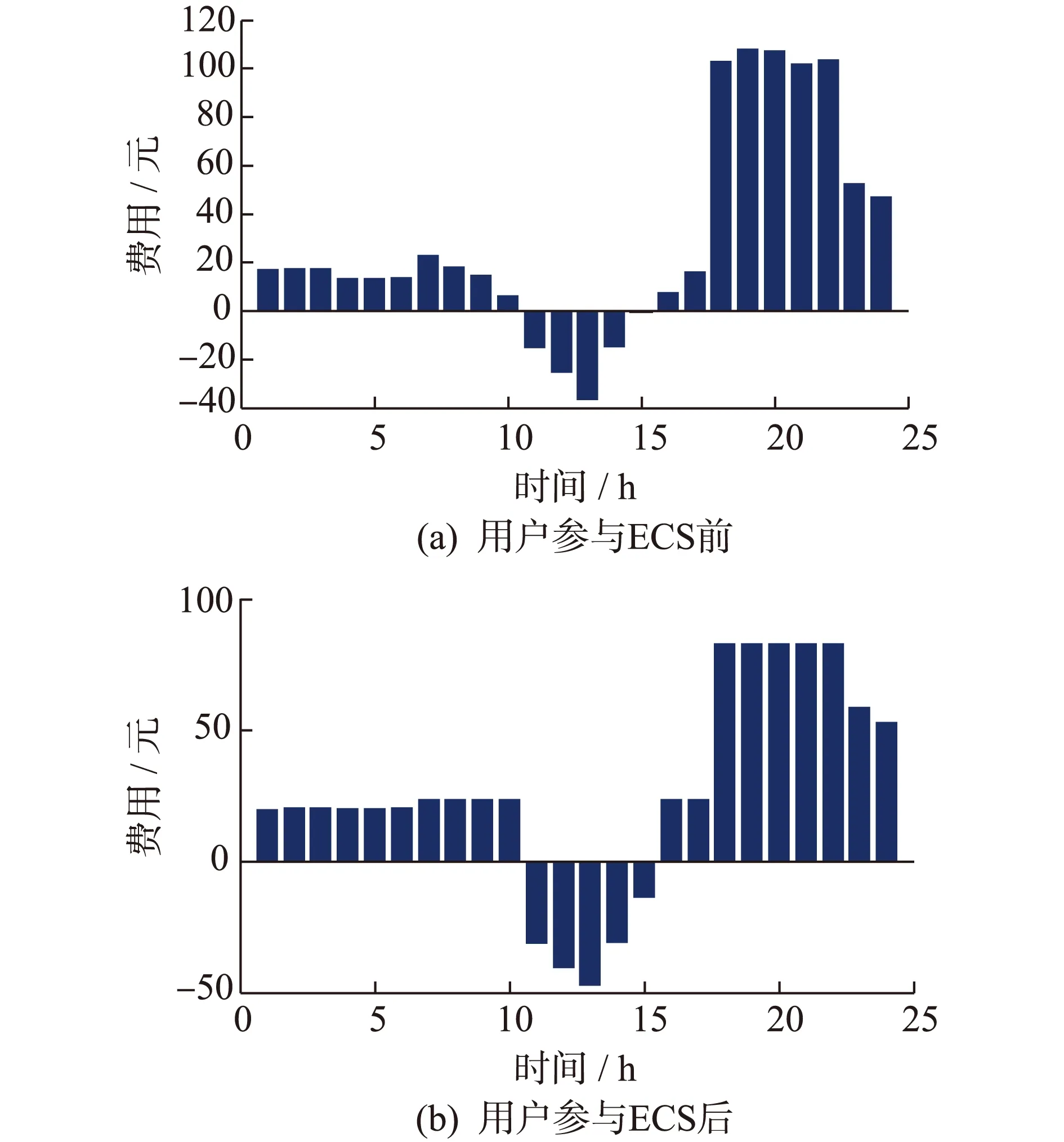
图5 用户参与ECS前后每小时总费用Fig.5 Users’ energy cost without/with ECS

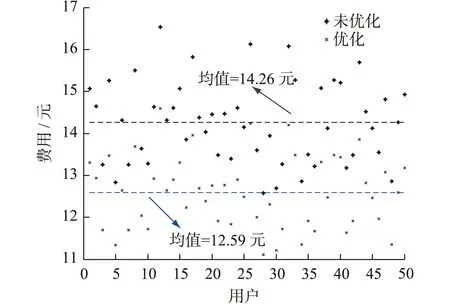
图6 用户参与ECS前后日能源费用Fig. 6 Users’ daily energy cost without/with ECS

4 结语

基于居民用户的负荷用电安排提出了一种合作博弈模型，并将光伏电池板以用户电能自发自用的方式引入到博弈模型中。利用一个小型智能电网系统对所提博弈模型进行验证，分析了用户参与负荷调度的合作博弈对用户本身和电力公司的影响。仿真结果表明，当用户参与能源消耗调度后，不仅用户电费减少，总负荷的PAR也降低，负荷分布趋于平缓。此外，当用户利用光伏电池板所发电量的剩余部分回售时，由于其获得售电收益，支付的电费将进一步减少。

本文暂未结合用户的用电行为特征对可转移负荷进行调度安排，因此，在后续研究中将重点研究用户行为习惯对可转移负荷优化调度的影响。

[1] 申展, 胡辉勇, 雷金勇, 等. 分布式电源接入用户及用户侧微电网双向电能计量问题[J]. 南方电网技术, 2015, 9(4): 14-21. SHEN Zhan, HU Huiyong, LEI Jinyong, et al. Bidirectional metering issues of user-side microgrid and user with distributed generation [J]. Southern Power System Technology, 2015, 9(4): 14-21.

[2] 张沈习, 李珂, 程浩忠, 等．考虑相关性的间歇性分布式电源选址定容规划[J]．电力系统自动化, 2015, 39(8) : 53-58. ZHANG Shenxi, LI Ke, CHENG Haozhong, et al． Optimal siting and sizing of intermittent distributed generator considering correlations [J]． Automation of Electric Power Systems, 2015, 39(8): 53-58.

[3] 吴桥, 卢树峰, 杨世海, 等. 需求侧响应条件下的家庭用电管理研究[J]. 江苏电机工程, 2016, 35(05): 28-31. WU Qiao, LU Shufeng, YANG Shihai, et al． Research on home energy management under the condition of demand-side response [J]． Jiangsu Electrical Engineering, 2016, 35(05): 28-31.

[4] SAMADI P, MOHSENIAN-RAD H, SCHOBER R, et al． Advanced demand side management for the future smart grid using mechanism design [J]． IEEE Transactions on Smart Grid, 2012, 3(3): 1170-1180.

[5] 梁甜甜, 高赐威, 王蓓蓓, 等．智能电网下电力需求侧管理应用[J]．电力自动化设备, 2012, 32(5): 81-85. LIANG Tiantian, GAO Ciwei, WANG Beibei, et al． Applications of demand side management in smart grid [J]． Electric Power Automation Equipment, 2012, 32(5): 81-85.

[6] ZHANG X． Optimal scheduling of critical peak pricing considering wind commitment [J]． IEEE Transactions on Sustainable Energy, 2014, 5(2): 637-645.

[7] DENG R, YANG Z, CHEN J, et al． Residential energy consumption scheduling: A coupled-constraint game approach [J]． IEEE Transactions on Sustainable Energy, 2014, 5(3): 1340-1350.

[8] 何永秀, 王冰, 熊威, 等．基于模糊综合评价的居民智能用电行为分析与互动机制设计[J]．电网技术, 2012, 36(10): 247-252. HE Yongxiu, WANG Bing, XIONG Wei, et al． Analysis of residents’ smart electricity consumption behavior based on fuzzy synthetic evaluation and the design of interactive mechanism [J]． Power System Technology, 2012, 36(10): 247-252.

[9] 卢强, 陈来军, 梅生伟, 等．博弈论在电力系统中典型应用及若干展望[J]．中国电机工程学报, 2014, 34(29): 5009-5017. LU Qiang, CHRN Laijun, MEI Shengwei, et al． Typical applications and prospects of game theory in power system[J]． Proceedings of the CSEE, 2014, 34(29): 5009-5017.

[10] YANG P, TANG G, NEHORIA A． A game-theoretic approach for optimal time-of-use electricity pricing [J]． IEEE Transactions on Power Systems, 2013, 28(2): 884-892.

[11] MAHARJAN S, ZHU Q, ZHANG Y, et al． Dependable demand response management in the smart grid: A Stackelberg game approach [J]． IEEE Transactions on Smart Grid, 2013, 4(1): 120-132.

[12] CHAI B, CHEN J, YANG Z, et al． Demand response management with multiple utility companies: A two-level game approach [J]． IEEE Transactions on Smart Grid, 2014, 5(2): 722-731.

[13] SOLA M, VITETTAG M. Demand-side management in a smart microgrid: A distributed approach based on Bayesian game theory [C]∥ 2014 IEEE International Conference on Smart Grid Communications, Venice, Italy, November 3-6, 2014: 656-661.

[14] MISRA S, BERA S, OJHA T, et al． ENTICE: Agent-based energy trading with incomplete information in the smart grid [J]. Journal of Network and Computer Applications, 2015, 55: 202-212.

[15] EKSIN C, DELIC H, RIBEIRO A, et al． Demand response management in smart grids with heterogeneous consumer preferences [J]. IEEE Transactions on Smart Grid, 2015, 6(6): 3082-3094.

[16] GAO B, ZHANG W, TANG Y, et al． Game-theoretic energy management for the residential users with dischargeable plug-in electric Vehicles [J]． Energies, 2014, 7(11): 7499-7518.

[17] KALLEL R, BOUKETTAYA G, KRICHEN L. Demand side man-agement of household appliances in stand-alone hybrid photovoltaic system [J]. Renewable Energy, 2015, 81: 123-135.

(编辑方晶)

Cooperative Game-based Energy Consumption TechnologyConsidering Household Distributed Generators

CHEN Bin

(Electric Power Research Institute, Fujian Electric Power Company Limited, Fuzhou 350007, China)

In smart grid, residential users who participate in demand side management can schedule household energy consumption appropriately according to the real-time energy price. This paper proposes a kind of energy consumption technology based on cooperative game by considering the participation of household distributed generators. Based on the presented power consumption model, energy cost model, and household load control model, energy consumption among residential users is formulated as a cooperative game; where players are residential users and strategies are their daily consumption schedule. The energy cost of all users is minimized at Nash equilibrium solution. Simulation result shows that users’ cost is decreased and further decreased with distributed generators when users participate in energy consumption scheduling with game approach.

demand side management; cooperative game; energy consumption scheduling; household distributed generators