城市电网耦合氢储能系统投资决策方法研究
2017-09-17邵志芳吴继兰
邵志芳, 吴继兰, 赵 强
(1. 上海财经大学信息管理与工程学院,上海 200433;2. 中国电力科学研究院,北京 100092)
城市电网耦合氢储能系统投资决策方法研究
邵志芳1, 吴继兰1, 赵 强2
(1. 上海财经大学信息管理与工程学院,上海 200433;2. 中国电力科学研究院,北京 100092)
针对城市电网负荷峰谷差大导致电力资源大量浪费的现状,提出城市电网耦合氢储能系统方案用于消纳电网负荷低谷时段富余电能。通过对氢储能系统运行周期内的投资成本和经济收益进行分析,构造投资决策评价模型,并根据投资者不同的投资需求建立三种优化模型:氢气最低销售价格模型、氢储能系统最优装机容量模型和特定投资回收期下氢气最低销售价格模型。以某城市电网用电负荷数据为基础,利用上述模型对在该城市实施城市电网耦合氢储能系统方案时不同投资需求下的最优方案进行了分析。
城市电网;氢储能系统;全生命周期成本;投资决策
0 引言
随着经济的快速发展和人民生活水平的逐步提高,我国工业、农业、服务业以及居民家庭的用电需求急剧增加,电网高峰时期用电负荷屡创新高。由于电网高峰负荷持续时间较短,导致为满足高峰负荷需求而规划建设的电力设备利用率较低。针对电网负荷低谷时期电力资源浪费的问题,很多学者进行了研究并提出了解决方案,包括谷电抽水蓄能[1]、电池储能[2,3]以及电解水制氢存储[4-6]等。其中氢气由于清洁无污染、可存储运输等特点被视为21世纪最具发展潜力的清洁能源。随着氢能应用终端技术的推广应用,对规模化清洁的氢能制取方式产生迫切需求。
城市电网耦合氢储能系统不仅可消纳电网负荷低谷时段的富余电能,同时还可解决一部分氢能应用终端产业的用氢需求[7-9]。文献[10]根据所生产氢气的3种用途:作为化工原料出售、作为氢能汽车燃料和氢气燃烧发电,对谷电制氢成本进行分析,得出作为化工原料出售经济性最好的结论。文献[11]建立多目标混合整数线性规划数学模型研究并网微网调度优化问题,该微网系统包括碱性电解池、压缩机和用于存储能量的燃料电池,结果显示该系统可平衡电网负荷。文献[12]对意大利中部的河流水力发电厂以氢能作为能源管理解决方案的适宜性从生命周期角度进行评估,考虑了谷电制氢存储以及用电高峰时氢燃料电池再发电,结果显示盈利性高于意大利传统电网电力盈利。
基于这一背景,文中提出城市电网耦合氢储能系统运行方案,利用全生命周期成本分析法,分析该系统的投资成本和收益,构建投资决策模型,并通过案例仿真分析,提出投资建议。可为城市电网耦合氢储能系统的商业化运行提供理论依据,为政府部门和相关投资者提供投资决策支持。
1 城市电网耦合氢储能系统方案
1.1 系统结构与流程
城市电网耦合氢储能系统是利用电网负荷低谷时期的多余电能进行电解水制氢,将富余电能转化为氢能存储使用。城市电网耦合氢储能系统如图1所示。

图1 城市电网耦合氢储能系统Fig.1 Diagram ofurban power grid coupled to hydrogen energy storage system
1.2 小时能量管理模型
氢储能系统的电解槽、压缩机等耗电装置利用富余电能进行电解水制氢。同时电能在传输的过程中存在能量损耗问题,能量转移过程如图2所示。由于用电负荷在一个自然天之内存在明显的高峰期和低谷期,所以氢储能系统的实际用电功率与其额定用电功率并不时刻相等。
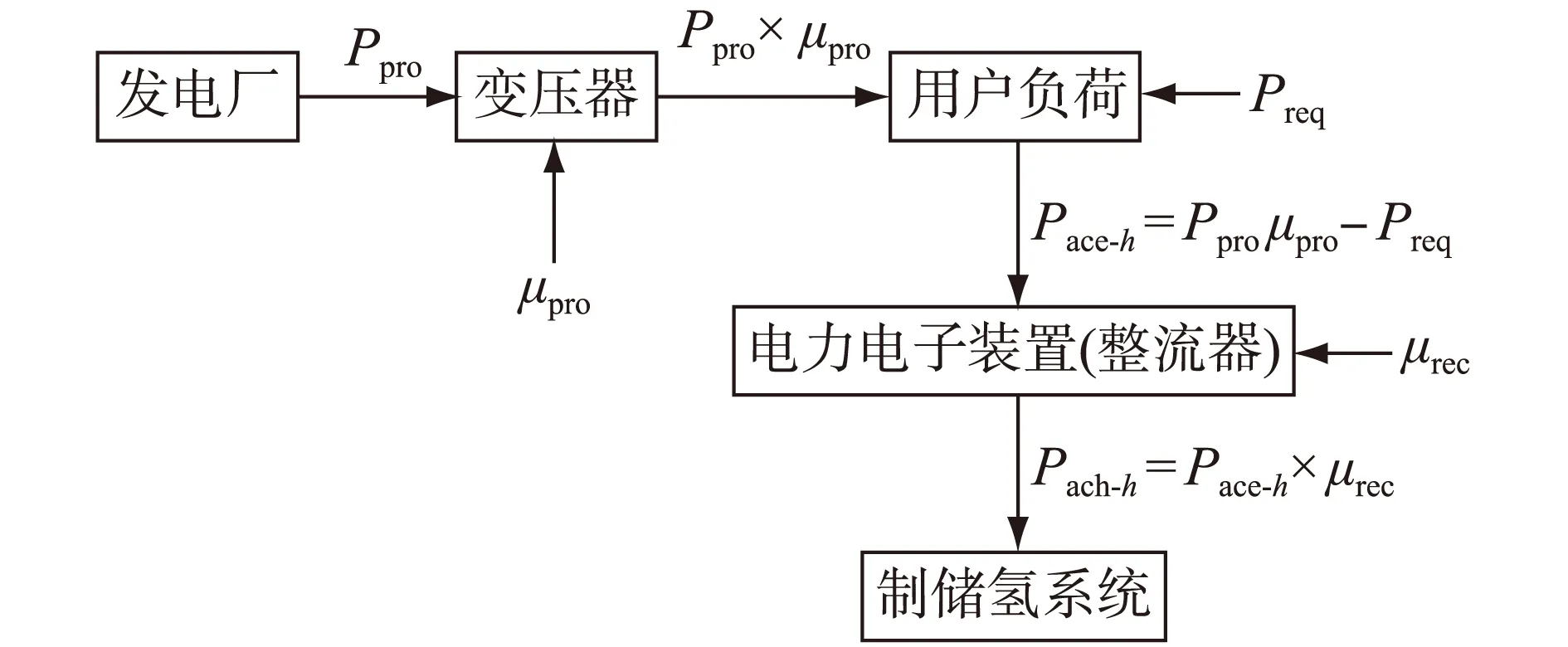
图2 电力传输能量转移图Fig.2 diagram of energy transfer
氢储能系统的实际用电功率可表示为:
Ppro×μpro-Preq=Pace-h
(1)
式中,Ppro为发电厂额定输出功率;μpro为变压器将电传输到电网的传送效率;Preq为用户的用电功率;Pace-h为电网剩余用电功率。
Pact-h=Pace-h×μrec
(2)
μrec为交流电转换为直流电时整流器的效率;Pact-h为将交流电转换为直流电后氢储能系统实际可利用的用电功率。
若Pele为氢储能系统额定用电功率,Pmin为最小用电功率,氢储能系统的实际用电功率Preal-h为:
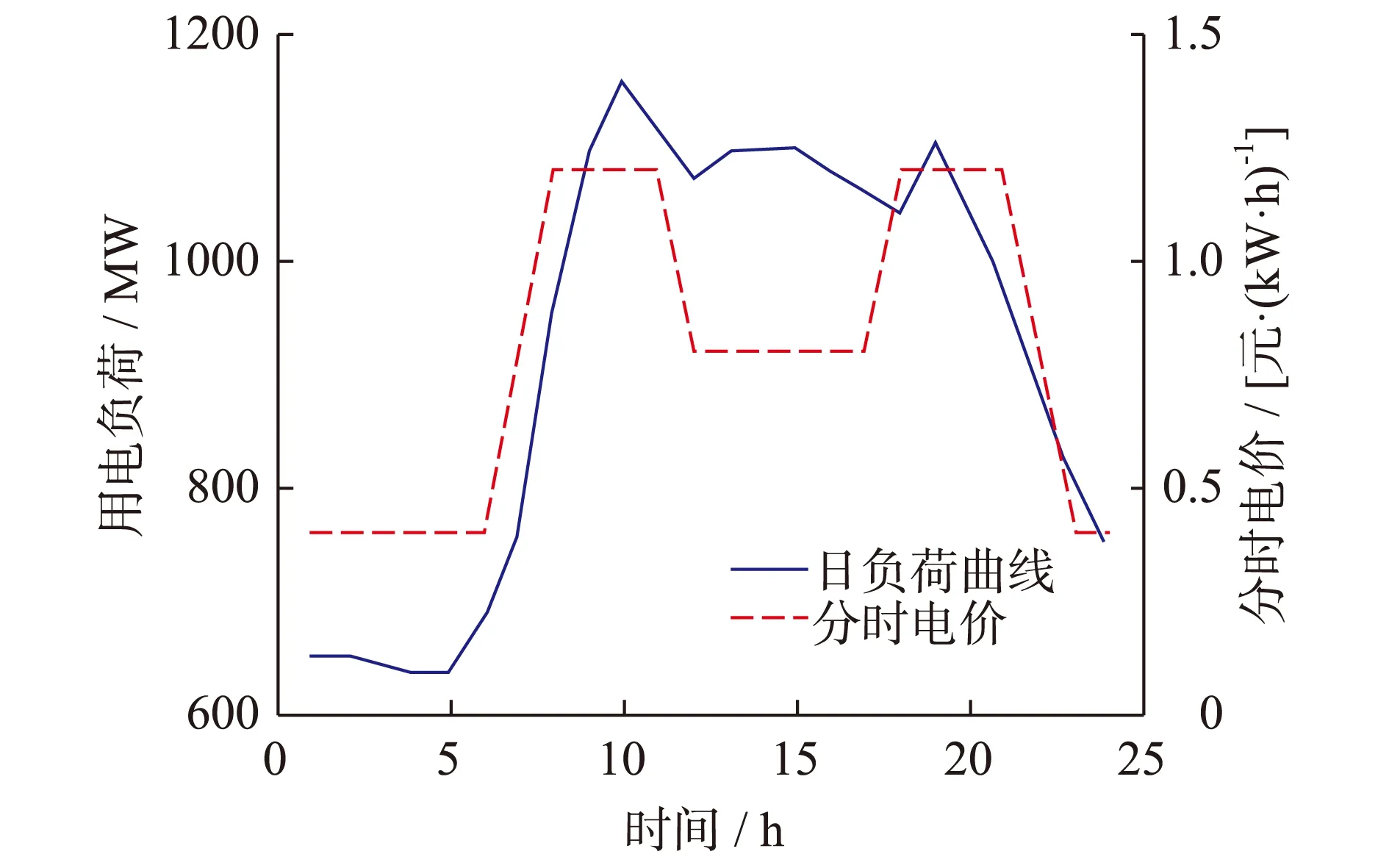
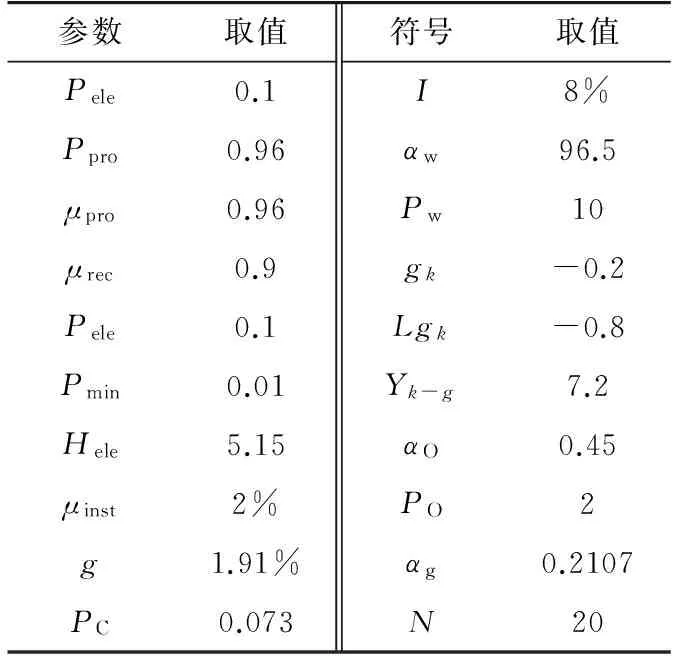
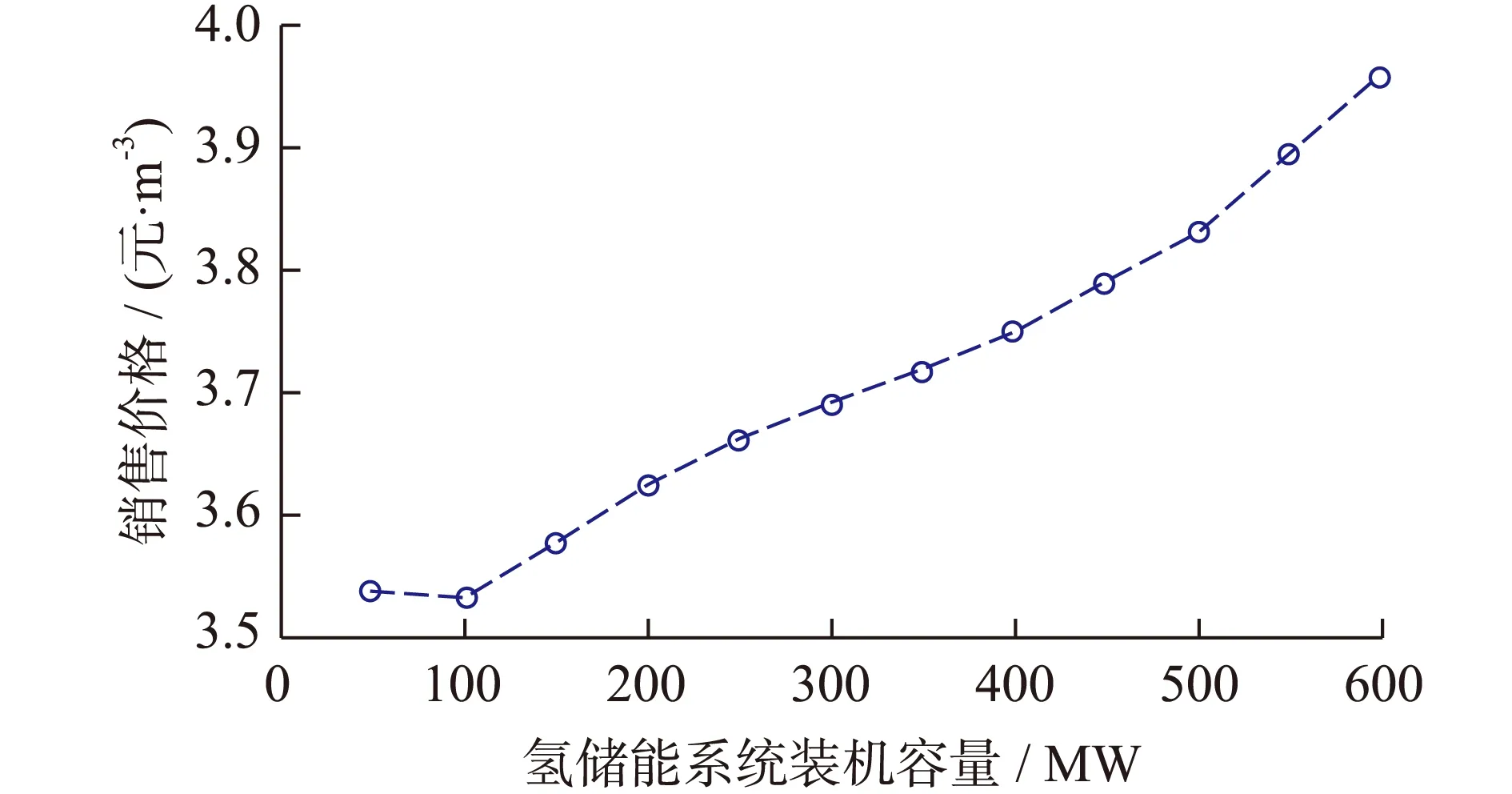
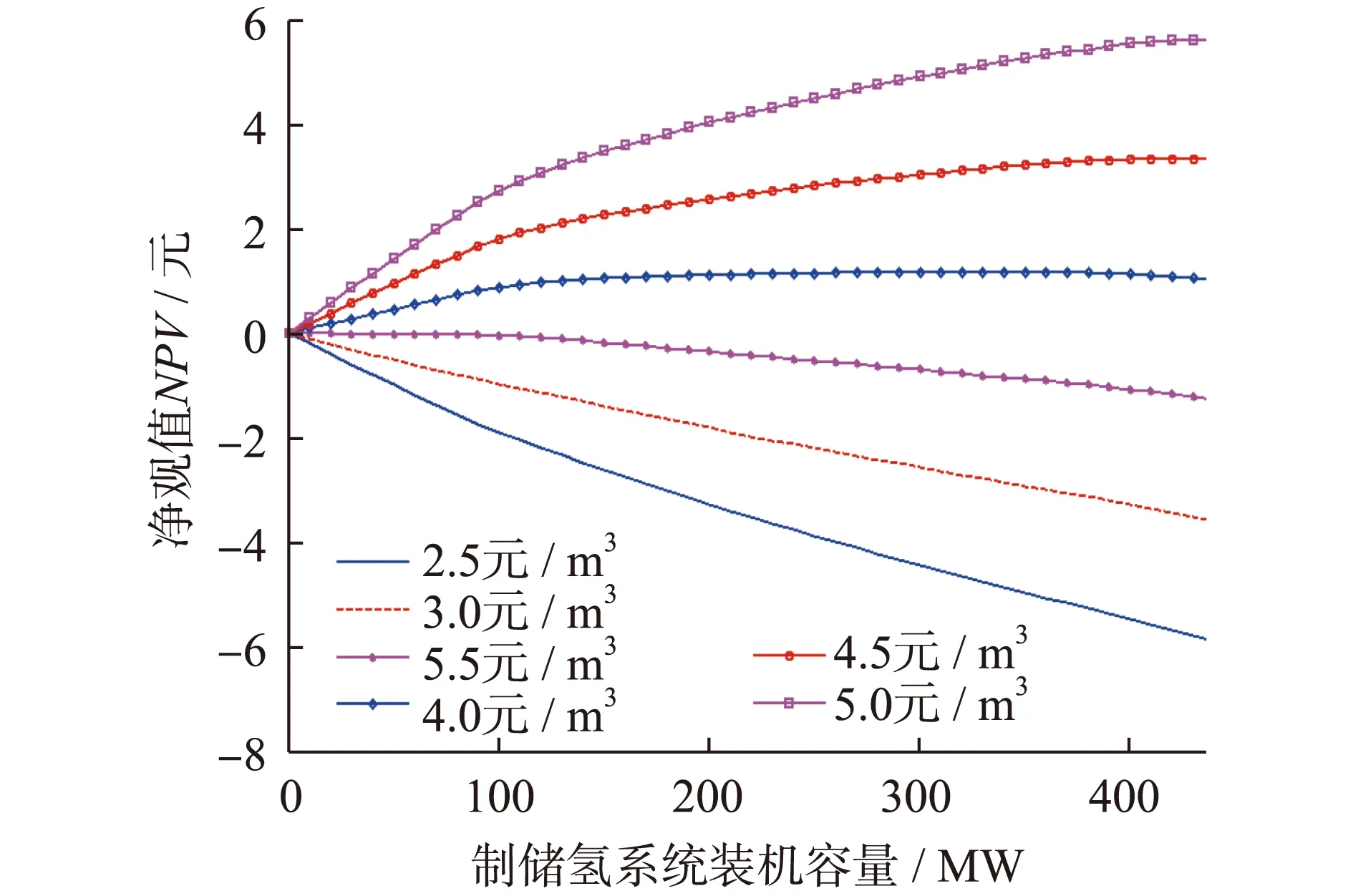
Preal-h=0Pact-h (3) Preal-h=Pact-hPmin≤Pact-h≤Pele (4) Preal-h=PelePele (5) 氢储能系统小时氢气产量取决于系统的实际用电功率,根据式(1—5),氢储能系统小时氢气产量计算如下: MH2-h=0Pact-h (6) (7) (8) 式中,MH2-h为氢储能系统的氢气产量;Hele为氢储能系统生产单位氢气的综合电耗;μele为氢储能系统的生产效率。 城市电网耦合氢储能系统的全生命周期成本指项目周期内所发生的费用之和,主要包括初期投资成本、运行维护成本、年直接成本和设备更新成本。 2.1 初期投资成本现值 初期投资发生在项目的前期,这部分资金不会受到通货膨胀的影响,因此氢储能系统的初期投资成本可以表示为: Cinvest=(∑Ck+Cland)(1+μinst) (9) 其中,Ck为氢储能系统设备k的购买成本,;Cland为建筑成本;μinst为氢储能系统设备安装集成等工程成本占初始投资成本的比例。 2.2 运行维护成本现值 运行维护成本现值NPCOM-k可表示为: (10) 其中,COM-k为设备k每年的运行维护成本;g为通货膨胀率;N为项目的执行时间;I为社会折现率。 2.3 年直接成本现值 用电成本现值NPCe表示为: (11) 用水成本现值NPCw可以表示为: (12) 式中,αw为生产单位氢气的耗水量;Pw为单位水的价格。 所以年直接成本现值NPCe-w可以表示为: NPCe-w=NPCe+NPCw (13) 2.4 氢储能系统设备更新成本现值 在氢储能系统运行周期内,设备因到达其使用寿命而产生更新行为。考虑技术进步的影响,设备的购买成本逐年降低,所以再次购买设备时的购买成本低于原始购买成本。具体价格受技术进步或通货膨胀率的影响,主要分以下两种情况:(1) 设备更新时间发生在技术进步期内,再次购买设备的价格随技术进步的速率发生改变,购买价格逐渐降低;(2) 设备更新时间发生在技术成熟期,此时设备的购买价格不随技术进步的速率发生改变,只受通货膨胀的影响。 设备k未来发生的更新成本折现到当期的现值NPCr-k可以表示为: (14) 式中,gk为设备k预期的年技术进步速率;Lgk为设备k预期极限技术进步速度;Lifek为设备k的使用期限;Yk-g为设备k到达预期极限技术进步速率时所花费的时间;Nrep-k为在氢储能系统生命周期内设备k的总更新次数;Nf-r-k为设备k的价格变化取决于自身通货膨胀率gk时设备k的总更新次数。Nrep-k,Nf-r-k和Yk-g的计算公式如下: (15) (16) (17) 城市电网耦合氢储能系统的收益主要包括销售氢气收入、销售氧气收入、碳减排收益和设备残值收益四部分,将通货膨胀率和社会折现率影响因素考虑在内,利用小时能量管理模型以每小时为单位对这四部分收益分别进行数学建模。 3.1 销售氢气收益现值 氢气销售收入是氢储能系统最主要的经济来源,这里考虑通货膨胀对氢气销售价格的影响,以每小时为单位计算系统每一年内的氢气产量并乘以氢气销售价格得到该年氢气的销售收益;同时,将每一年的收益折现到初期并累加求和得到系统运行周期内的总氢气销售收益。 (18) 式中,NPVH2销售氢气收益现值;PH2为单位氢气的销售价格。 3.2 销售氧气收益现值 氢储能系统生产氢气的同时会产生副产物氧气,考虑通货膨胀对氧气销售价格的影响,可得销售氧气收益现值NPVO为: (19) 其中,αO为生产单位氢气的产氧量;PO为单位氧气的价格。 3.3 碳减排收益现值 根据氢气产生热量与汽油产生热量的对等原则,利用碳交易准则将碳减排收益进行货币化处理。考虑通货膨胀对碳交易价格的影响,以每小时为单位计算系统每一年内的碳减排数量并乘以碳交易价格得到该年碳减排收益。可计算出氢储能系统的碳减排收益NPVC为: (20) 其中,αg为单位氢气燃烧产生的热能与汽油燃烧产生的热能等价时,氢气替代汽油燃烧而减少的碳排放数量;PC为碳交易价格。 3.4 残值收益现值 首先考虑技术进步导致设备价格降低和通货膨胀对设备价格的影响,计算系统运行周期结束时设备的价格;其次,以设备在系统运行周期结束时剩余的使用寿命对残余价值进行衡量得到残值收益,可计算出残余收益现值NPVend-k为: (21) 4.1 投资决策评价模型 4.1.1 净现值模型 氢储能系统的净现值NPV是系统使用期限内现金流入现值(即收益现值)与现金流出现值(即成本现值)的差值。当NPV≥0时,说明该投资项目是经济可行的,特别当NPV>0时,净现值越大该方案的经济可行性越好;反之,说明该投资项目不具有经济可行性。由式(18—21),可得NPV的计算表达式如下: NPV=NPVH2+NPVO+NPVC+∑NPVend-k- (22) 4.1.2 内部收益率模型 内部收益率IRR指项目现金流入量现值等于现金流出量现值时的社会折现率,其经济含义表示项目在运行时间内为收回投资每年的净收益率。令NPV=0,此时求得的I值即为内部收益率IRR。当IRR≥I时,表明该投资项目是经济可行的;反之,该项目不可行。根据式(18—21),内部收益率IRR可通过(23)式求得。 NPVH2+NPVO+NPVC+∑NPVend-k-Cinvest- ∑NPCOM-k-NPCe-w-∑NPCr-k=0 (23) 4.2 特定目标下投资决策优化模型 4.2.1 氢气最低销售价格模型 项目投入运行后其预期净现值等于零时的氢气价格便是氢气的最低销售价格,低于此价格项目将无法盈利。氢气的最低销售价格见式(24)。 (24) 4.2.2 最优装机容量模型 氢储能系统具有投资可行性的前提是净现值大于等于零,净现值越大,投资收益越高。由净现值NPV的计算表达式可知净现值受氢气销售价格和系统装机容量的影响,投资者可以通过在可取的范围内控制这两个变量的取值从而改变净现值的数值。在给定氢气销售价格的情况下,在装机容量允许范围内逐渐增大装机容量,利用小时能量管理模型仿真计算各装机容量下每小时的氢气产量,同时利用净现值模型计算该装机容量下的净现值,可得到给定氢气销售价格下氢储能系统装机容量和净现值的关系曲线。当净现值存在大于等于零的情况时,最优装机容量即为净现值最大时对应的装机容量。由此,最优装机容量为公式(25): maxNPV-pele=NPVH2+NPVO+NPVC+ (25) 4.2.3 特定投资回收期下氢气最低销售价格模型 氢气销售价格对项目的投资回收期有很大影响,当项目投资者给定项目的投资回收期后,为了收回投资成本,氢气最低销售价格便需要随之确定。假定项目的投资回收期为n,那么氢气最低销售价格见式(26)。 (26) 5.1 案例背景与数据 以某城市电网为研究对象进行分析,该城市电网某天的历史用电日负荷曲线如图3中实线所示,可见该城市用电负荷曲线存在明显的峰谷差且曲线波动显著。 图3 日负荷曲线与工业分时电价Fig.3 Daily load curve and industrial TOU price 根据现有文献[13-16]及专家意见,氢储能系统投资决策模型中的有关参数取值见表1。 其中通货膨胀率g的取值,通过选取我国1995年至2014年的消费者价格指数数据,采用移动平均法对通货膨胀率进行预测,计算得出。案例分析部分按照城市电网氢储能系统生产的氢气均可以全部售出进行计算。 表1 主要参数取值表Table 1 Main Parameter values 5.2 案例分析 5.2.1 氢气最低销售价格分析 净现值大于等于零时,氢储能系统的方案具有投资可行性,特别当净现值等于零时,方案到达投资可行性的临界点,此时求得的氢气销售价格便是氢储能系统在不同装机容量下对应的最低销售价格。 图4 不同装机容量下氢气最低销售价格Fig.4 The minimum selling price of hydrogen under different installed capacity 如图4所示,图中的曲线为等净现值线,曲线上的点为氢储能系统在不同装机容量下满足净现值等于零时的氢气最低销售价格,例如氢储能系统的装机容量为200 MW时,由图4可知氢气的最低销售价格应达到3.623元/m3(标准状态下,下同)项目才有可行性。 氢储能系统装机容量不同,谷电利用率和系统闲置率亦不同。图5表示装机容量从0 MW逐渐增加到700 MW时各装机容量对应的谷电利用率与系统闲置率。可见,氢储能系统装机容量的提高会导致谷电利用率和系统闲置率的同时提高。因此,如何对这两个因素进行取舍取决于投资者的出发点。如果投资者希望提高谷电利用率,则可适当增加氢储能系统装机容量;如果投资者希望降低氢储能系统的闲置率,则需减小氢储能系统的装机容量。 图5 谷电利用率与系统闲置率Fig.5 Valley electricity utilization and system idle rate 5.2.2 最优装机容量分析 以氢气销售价格为3元/m3作为基准价格,将价格上下浮动一定幅度对最优装机容量进行分析,如图6所示。可见,在其他因素不变的情况下,氢气销售价格分别为2.5,3.0,3.5元/m3时,项目净现值均小于零,即不具有投资可行性;当氢气销售价格高于4.0元/m3时,氢储能系统装机容量在一定范围内均可以使方案具有投资可行性。 图6 不同氢气价格下氢储能系统最优装机容量Fig.6 Optimal installed capacity of hydrogen storage ystem under different hydrogen prices 当氢气销售价格为4.0元/m3时,氢储能系统装机容量为350 MW时净现值取得最大值,投资效益最好。此时,电网日负荷曲线和谷电利用率分别如图7和图8所示(谷电利用率为0表示此时电网无可利用电能)。同理可得氢气销售价格为4.5元/m3、5.0元/m3时最优装机容量以及电网日负荷曲线和谷电利用率。 图7 装机容量为350 MW时电网负荷曲线Fig.7 Load curve of power system with 350 MW installed capacity 图8 装机容量为350 MW时谷电利用率Fig.8 The utilization ratio of valley electricity when the installed capacity is 350 MW 对比上述三种最优装机容量下用电负荷曲线和谷电利用率曲线得:随着氢气价格的增加,氢储能系统最优装机容量、谷电利用率、系统闲置率和经济效益均表现出增大的趋势,如表2所示。若希望其闲置率最低,采用氢气销售价格达到4.0元/m3,匹配350 MW装机容量的方案;若希望谷电利用率最高,则采用氢气销售价格达到5.0元/m3,匹配490 MW装机容量的方案。 表2 不同氢气价格下最优方案经济数据Table 2 Economic data of optimal scheme under different hydrogen price 针对目前我国电网负荷峰谷差大、用电负荷低谷时段富余电能严重浪费和传统能源有限且不可再生的两大问题,文中提出了城市电网耦合氢储能系统方案。该方案不仅可以从需求侧的角度出发有效利用浪费的电力资源,达到减小负荷峰谷差平滑负荷曲线的作用,同时可以将产出的氢气作为氢能源汽车的燃料替代传统汽油能源,从而实现清洁替代,有效减少环境污染。在此基础上,构建了城市电网耦合氢储能系统的投资决策模型,并通过实际案例对模型应用进行了解析,从而为不同投资决策需求下的投资者提供最优决策建议。 城市电网耦合氢储能系统的生命周期相对较长,在实际投资决策过程中会受到诸多不确定性因素的影响。限于篇幅,本文暂未进行各种因素的不确定性分析。为了使方案的投资决策分析更加准确,后续研究将会进一步进行相关因素的敏感性分析和风险分析。 [1] 黄亚斌,刘国刚,文福拴,等. 电力市场环境下抽水蓄能电站的运营模式与效益分析[J]. 电力科学与工程, 2006(3): 56-62. HUANG Yabin, LIU Guogang, WEN Fushuang et al. A preliminaryinvestigation on operating modes and benefit analysis of pumped storage power plants in electricity market environment[J]. Electric Power Science and Engineering, 2006(3): 56-62. [2] 韩晓娟,田春光,张 浩,等. 用于削峰填谷的电池储能系统经济价值评估方法[J]. 太阳能学报,2014, 35(9): 1634-1638. HAN Xiaojuan,TIAN Chunguang,ZHANG Hao,et al. Economic evaluation method of battery energy storage system in peak load shifting[J]. Acta Energiae Solaris Sinica, 2014, 35(9): 1634-1638. [3] 修晓青,李建林,惠 东. 用于电网削峰填谷的储能系统容量配置及经济性评估[J]. 电力建设, 2013, 34(2): 1-5. XIU Xiaoqing, LI Jianlin, HUI Dong. Capacity configuration and economic evaluation of energy storage system for grid peak load shifting[J]. Electric Power Construction, 2013, 34(2): 1-5. [4] 熊 雄,杨仁刚,叶 林,等. 电力需求侧大规模储能系统经济性评估[J]. 电工技术学报, 2013, 28(9): 224-230. XIONG Xiong, YANG Rengang, YE Lin, et al. Economic evaluation of large-scale energy storage allocation in power demand side[J]. Transactions of China Electrotechnical Society, 2013, 28(9):224-230. [5] 方世杰,邵志芳,张存满. 并网型风电耦合制氢系统经济性分析[J]. 能源技术经济, 2012, 24(3): 39-43. FANG Shijie, SHAO Zhifang, ZHANG Cunman. Economic analysis on on-grid wind power coupling with hydrogen-production system[J]. Energy Technology and Economics, 2012, 24(3):39-43. [6] SHERIF S A, BARBIR F, VEZIROUGLU T N. Wind energy and the hydrogen economy-review of the technology[J]. Sol Energy, 2005,78(5): 647-660. [7] TSUTOMU O, KOICHI W. Feasibility study on hydrogen refueling infrastructure for fuel cell vehicles using the off-peak power in Japan[J]. International Journal of Hydrogen Energy, 2004,29(4): 347-354. [8] FLOCH P H, GABRIEL S, MANSILLA C, et al. On the production of hydrogen via alkaline electrolysis during off-peak periods[J]. International Journal of Hydrogen Energy, 2007,32(18): 4641-4647. [9] GRADITI G, TELARETTI E, TELARETTI E, et al. Technical and economical assessment of distributed electrochemical storages for load shifting applications: An Italian case study[J]. Renewable and Sustainable Reviews, 2016,57(5): 515-523. [10] LI Y, CHEN D W , LIU M., et al. Life cycle cost and sensitivity analysis of a hydrogen system using low-price electricity in China[J]. International Journal of Hydrogen Energy, 2017, 42(4): 1899-1911. [11] LUCAS B J, ANKE W. Optimal microgrid scheduling with peak load reduction involving an electrolyzer and flexible loads[J]. Applied Energy, 2016, 169(5): 857-865. [12] ANTONIO V, DIEGO I, JAVIER D, et al. Life-cycle performance of hydrogen as an energy management solution in hydropower plants: A case study in central Italy[J]. International Journal of Hydrogen Energy,2015, 40(46): 16660-16672. [13] 林旭清,张思雨,孙 权,等. 新能源发电制氢储能技术探究[J]. 科技资讯, 2015,13(24): 25-26. LIN Xuqing, ZHANG Siyu, Sun Quan, et al. Research on hydrogen energy produced by new energy storage technology[J]. SCIENCE & TECHNOLOGY INFORMATION, 2015, 13(24): 25-26. [14] 赵振宇,李志伟,姚 雪. 基于碳减排收入的风电成本电价研究[J]. 可再生能源, 2014, 32(5): 662-667. ZHAO Zhenyu, LI Zhiwei, YAO Xue. Study on cost price of wind power electricity based on the certified emission reduction income[J]. Renewable Energy Resources, 2014,32(5): 662-667. [15] OLDRICH J. Advanced polytropic calculation method of centrifugal compressor[C]∥ ASME 2010 International M-e-c-h-a-n-i-cal Engineering Congress and Exposition. American Society of Mechanical Engineers, 2010: 123-31. [16] SCHOENUNG S. Economic analysis of large-scale hydrogen storage for renewable utility applications[C]∥ International Colloquium on Environmentally Preferred Advanced Power Generation, 2011: 8-10. (编辑方 晶) Investment Decision Method of Coupled Hydrogen Energy Storage System in Urban Power Grid SHAO Zhifang1,WU Jilan1, ZHAO Qiang2 (1. School of Information Management and Engineering, Shanghai University of Finance and Economics,Shanghai 200433, China;2. China Electric Power Research Institute,Beijing 100092, China) The peak-valley load difference of urban power grid leads to a large waste of power resources. Urban power network couped to hydrogen energy storage system is proposed here to dissipate surplus power during low load period. Based on the analysis of investment cost and economic benefit in the life cycle of hydrogen storage system, an evaluation model for investment decision making is built which involves three optimization models according to the different investment demands: the minimum hydrogen selling price model, the optimal installed capacity model and minimum selling price model under given payback period. Finally, based on the real data of a certain city grid load, the optimal scheme is analyzed under the different investment demand when the urban power grid coupled to hydrogen energy storage system is implemented in the city. urban power grid; hydrogen energy storage system; life cycle cost; investment decision 邵志芳 2017-04-13; 2017-05-27 国家863计划资助项目(2014AA052501);国家电网公司科技项目(2015110461) TK01+8 :A :2096-3203(2017)05-0045-07 邵志芳(1975—),女,河北石家庄人,博士,副教授,从事新能源经济与仿真优化研究工作(E-mail:shao.zhifang@mail.shufe.edu.cn); 吴继兰(1978—),女,山东潍坊人,博士,讲师,从事新能源经济与仿真优化研究工作(E-mail:wujilan@mail.shufe.edu.cn); 赵 强(1978—),男,辽宁沈阳人,高级工 程师,从事电力系统稳定分析研究工作(E-mail:zhaoqiang@epri.sgcc.com.cn)。
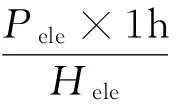
2 全生命周期成本现值分析


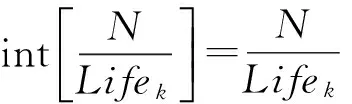

3 收益现值模型

4 投资决策模型
Cinvest-∑NPCOM-k-NPCe-w-∑NPCr-k
∑NPVend-k-Cinvestment-∑NPCOM-k-
NPCe-w-∑NPCr-k
5 案例研究




6 结语

