口算乘法教学的“四部曲”

◎洪菲菲

口算乘法教学的“四部曲”

◎洪菲菲

人教版《义务教育教科书·数学》三年级上册“口算乘法”一课的教学，是在学生学习了表内乘法的基础上进行的。口算乘法的教学不同于笔算乘法，有它独有的特点及方式，对于后续笔算乘除法的教学亦有着重要的铺垫作用。下面，笔者以“12×3”这道例题的教学为例，谈谈口算乘法的教学。

一、直观操作，理解算理

学生对口算算理的理解，要从直观的实物操作开始。通过对小棒的拼摆，可以将抽象的口算算式化为直观的形象图示。在摆一摆、算一算、说一说的过程中，学生对于口算的算理有了较为深入的掌握。

师：12×3到底等于多少呢？请同学们用小棒摆一摆，再算一算，和同桌说一说是怎么计算的？

（学生摆小棒）

师：哪组小朋友愿意上来展示一下自己摆的小棒，并说说自己的算法？

（展示小棒，如图1）

生1：可以用12+12+12=36。

师：这位小朋友将乘法转化成加法，算出了得数，真不错。有没有不一样的方法呢？

生2：先算整捆的小棒，用10×3等于30；再算单根的小棒，用2×3等于6。最后将30加6等于36。

师：哪一种方法更简单一些？

生3：第二个同学的方法更简单。

图1

师：我们再来回顾一下第二位同学是怎么计算的，你们看。 （课件展示，如图2）

师：计算这道题，我们先做什么，再做什么，最后做什么？谁能再来说一说？

生4：我们先把12×3分成10×3和2×3两个算式，接着我们算出两个算式的得数，10×3=30，2×3=6；最后再把两个算式的得数加起来，30+6=36。

图2

师：也就是说，我们经过了“分—算—合”三步，对吗？（板书：分→算→合）

在上述教学中，学生通过摆小棒，自主找寻计算12×3的方法。在小棒的直观帮助下，学生很容易地找寻到计算这道题的两种方法。将乘法转化为加法来计算，符合学生原有的认知基础，但这样的计算方法并不简便。在小棒的直观提示下，学生找到了另一条捷径——将整捆的小棒和单根的小棒分开来算，得到10×3和2×3两道算式，分别算出结果之后再将两个得数相加。对比之下，学生感受到了用乘法思维进行计算的优越性，并提炼出了“分—算—合”的计算方法。直观操作，为学生理解算理提供了强有力的支撑，也是学生提炼算法的重要基础。

二、形成导图，铺设桥梁

在充分的实物操作之后，学生能够依托“数小棒”算出得数。然而，小棒只是学习的“拐杖”，学生不能对之产生依赖。而直接由实物的直观操作过渡到口算方法的提炼，又显得有些操之过急，两者之间出现了一些思维空白。为了使口算教学更加“细腻”，我们有必要在“算理”和“算法”之间架设一座桥梁，帮助学生更好地实现“理”“法”之间的过渡。

师：刚才，我们通过摆小棒，计算出了12×3的得数。如果没有了小棒的帮忙，你们还能口算出其他算式的结果吗？

（板书：12×4）

师：这道题该怎么算呢？想想刚才我们摆小棒的过程。谁来试一试？

生：可以把12分成10和2，那么，12×4就可以分成10×4和2×4两个算式。10×4等于40，2×4等于8，40加8等于48。

（教师根据学生的回答进行板书，如图3）

图3

师：你们能像他这样，不摆小棒也能算出乘法算式的结果吗？拿出老师为你们准备的口算单（如图4），自己算一算，填一填，再和同桌小朋友说一说。

（学生填口算单，同桌交流，指名展示汇报。）

图4

学生在经历了摆小棒之后，对两位数乘一位数（不进位）的口算方法有了初步的感知。如果没有及时对操作过程进行抽象和提炼，学生仍旧不能很好地进行口算。这时，利用思维导图是一个很好的辅助手段。通过建构导图，有利于学生脱离直观操作，梳理计算流程，对于后续形成算法起着重要的过渡作用。在上述教学环节中，教师先引导学生回顾摆小棒的过程，尝试着描述计算过程，教师根据学生的描述逐步形成思维导图。在学生“试水”之后，教师再引导学生独立填写口算的思维导图，使每个学生都能在脑海里经历“梳理”的过程，帮助学生实现了从直观操作到思维导图的抽象提升。

三、思维内化，提炼算法

学生通过导图的梳理，对如何进行乘法口算有了较好的掌握。然而，“会算”并不是口算的最终目标。口算与笔算的不同之一，就在于它要求学生快速地在脑海里进行一系列思维活动，并将口算得数脱口而出。要实现其中的“快”“准确”等计算要求，学生就不能满足于“会算”，而应该在前面充分的直观操作、理解算理的基础上，对算法进行提炼。

师：同学们，你们都能算出口算乘法的结果了，真棒。有位小朋友丽丽，也想分享一下她的算法，你们想听听吗？播放课件。（如图5，并配以画外音：我是这样想的，把20×2记在心里，直接说出得数40；把3×2记在心里，直接说出得数6，得数是46。）

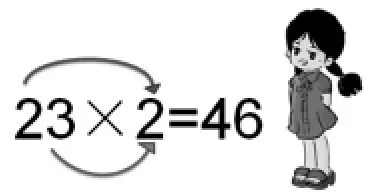
图5

师：这个方法怎样？对，美美觉得这个方法很好，也想来试试。播放课件。（如图6，并配以画外音：我也来试试，四十……六）

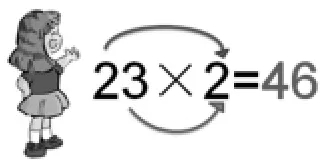
图6

师：同学们，你们觉得这个方法怎样？

生1：非常简便。

师：你们能像这两位小朋友一样，把计算过程想在心里，直接说出得数吗？

生2：能。

师：拿出老师为你们准备的口算卡片，同桌互相考一考，算一算，看谁算得又对又快。

（同桌进行口算活动）

学生通过摆小棒、填导图等活动，已经初步掌握了两位数乘一位数（不进位）口算的方法。虽然过程并不难，但相比以前表内乘法而言，程序要复杂了许多。如果仅停留在导图思维阶段，学生的运算速度就难以得到提升。因此，有必要对计算方法进行进一步的提炼。在上述教学环节中，教师借由两个小朋友之口，向学生提示了快速口算的方法——将计算过程想在心里，将得数脱口而出。课件当中算式里两个箭头的出现，直观提示了学生思考的方向。从高位开始，经由两句口诀（二二得四、二三得六），再结合数字所在的位值，就可以快速说出结果。其原理与摆小棒、填导图一脉相承，但较之前面的操作、导图等手段而言更为抽象。这种口算方法的习得，是在学生充分的操作、思考的基础上形成的，水到渠成，自然无痕。之后，教师引导学生进行同桌之间的口算练习，以帮助学生掌握计算方法，并形成快速准确地口算的技能。

四、总结提升，深化认知

如果教师将教学目标定位在能够快速准确地进行口算，学生能习得的只有技能。虽然技能也是教学的“双基”之一，但它只停留在学习的浅层部分。要让一节看似简单的口算教学课具有深度和意味，挖掘其背后的基本数学思想方法是很重要的。在课的最后，教师有必要带领学生对学习过程进行回顾梳理，并适时进行提升。

师：孩子们，今天这节课我们学习了什么内容？

生1：乘法口算。

生2：表外乘法。

师：为什么说是表外乘法呢？

生3：之前我们所学的乘法算式，都可以通过口诀直接得到结果。今天的乘法算式，在口诀表里找不到。

生4：我不太同意他的说法。今天的乘法算式虽然不能在口诀表里找到，但我们把它变成了可以用口诀计算的算式。比如，23×3这道题，我们可以通过“二三得六”和“三三得九”两句口诀，算出结果69。

师：我觉得这两位同学的回答都十分精彩。确实，今天的乘法口算，超出了口诀表的范围，我觉得“表外乘法”这个说法很形象，很有意思。后面这位同学归纳得也非常棒。当遇到新问题的时候，我们总是想办法把它转化为学过的知识，这是我们学习数学的金钥匙。

从一定程度上来说，计算的学习就是不断转化的过程。无论哪一种运算教学，我们总在经历将新知转化为旧知的过程。在口算教学的过程中，我们不能只满足于学生能够快速准确地口算，更重要的是让学生体会探索计算新知的方法——转化。在上述教学环节中，教师引导学生对整节课的学习进行回顾和梳理，学生既感受到了两位数乘一位数与之前口诀计算的不同，更主动找到了两者之间的联系——我们在口算两位数乘一位数的乘法算式时，将它转化成了两句口诀进行计算。教师在学生充分表达的基础上进一步提炼，使学生感受到了转化在计算学习中的重要作用，给了学生一把继续探索计算世界的金钥匙。

口算是笔算的基础，也是数学学习的根基之一，其重要性不言而喻。口算教学之所以没有受到足够的重视，是因为教师对口算内容的解读过于肤浅，对口算教学价值取向的认识过于片面。从直观操作到理顺思维，从提炼算法到升华认知，这样的学习经历对学生而言，其收获远不止技能的获得。教师能够把教学目标定位得准，把教材内容解读得深，把教学过程设计得巧，那么，简单的口算教学也能带给学生深远的影响和满满的收获。

（作者单位：福建省厦门实验小学集美分校）

（责任编辑：杨强）