多元均值不等式的构造策略
2017-09-16山东省寿光现代中学张靖涵
山东省寿光现代中学 张靖涵
多元均值不等式的构造策略
山东省寿光现代中学 张靖涵
均值不等式是求解最值、证明不等式的常用工具,其中“正”、“定”、“等”是该不等式应用的三个原则,而构造定值是应用的关键,特别对于存在多个变量的不等式问题,本文对多元均值不等式的构造策略举例探究如下。
策略一:整体性原则
例1 已知正实数x,y满足xy+2x+y=4,则x+y的最小值为________。
思路分析:本题所求表达式x+y刚好在条件中有所体现,所以考虑将x+y视为一个整体,将等式中的项往x+y的形式进行构造,y+2x+y=xy+x+(x+y)=x(y+1)+(x+y),而x(y+1)可以利用均值不等式化积为和,从而将方程变形为关于x+y的不等式,解不等式即可。

【点评】本题含有两个变量x,y,直接应用均值不等式缺少“定值”这一重要条件,而将x+y视为一个整体,在此基础上应用均值不等式,将x(y+1)转化为x+y+1,从而将方程变形为关于x+y的不等式,解不等式即可。
策略二:拆分项的策略
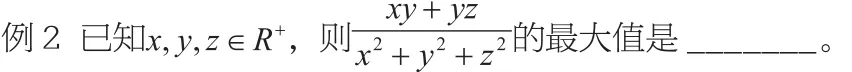
思路分析:本题变量个数较多且不易消元,考虑利用均值不等式进行化简,要求得最值则需要分子与分母能够将变量消掉,观察分子y,yz均含y,故考虑将分母中的y2拆分,与x2,z2搭配。

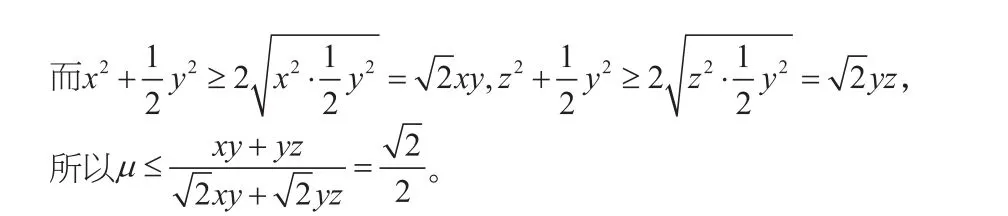
【点评】本题在拆分y2时还有一个细节:因为分子xy,yz的系数相同,所以要想分子分母消去变量,则分母中xy,yz也要相同,从而在拆分y2的时候要平均地进行拆分(因为x2,z2系数也相同)。所以利用均值不等式消元要善于调整系数,使之达到消去变量的目的。
策略三:参数分离法
例3 已知正实数x,y满足x+y+3=xy,若对任意满足条件的x,y,都有恒成立,则实数a的取值范围为________。
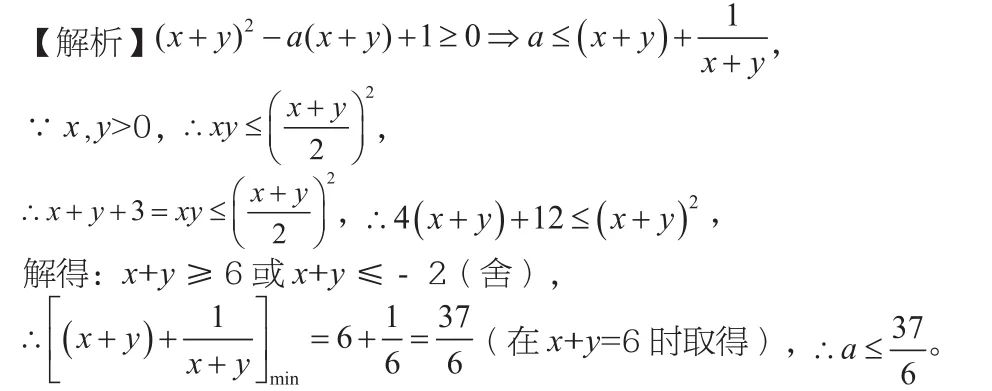
【点评】本题通过参数分离即可得到积为定值的模型,而难点在于求得x+y的取值范围,而已知关系式x+y+3=xy中既有x+y又有xy,故考虑均值定理转化为x+y的不等式,通过解不等式获得x+y的取值范围。
在上述问题中,要构造均值不等式,首先要从“定值”入手,其基本策略为:观察结构,合理变形,“定值”优先,巧借整体,化多元为一元,尤其要防范“等号”不成立带来的错误。
