基于反推法的非完整系统反馈控制问题研究

鞠桂玲， 罗俊芝， 要俊杰， 顾 娟, 刘兴华

(1. 装甲兵工程学院基础部， 北京 100072； 2. 中部战区，北京 100144)

基于反推法的非完整系统反馈控制问题研究

鞠桂玲1， 罗俊芝1， 要俊杰1， 顾 娟1, 刘兴华2

(1. 装甲兵工程学院基础部， 北京100072；2. 中部战区，北京100144)

针对一类具有不确定项非完整系统的反馈控制问题，结合滑模变结构控制和反推法，研究了其反馈控制器的设计问题。首先采用状态-状态转换技术对系统进行转换，使系统满足三角结构，然后运用反推法设计了系统的反馈控制器，最后通过数值模拟验证了所设计的反馈控制器的有效性。

状态-状态转换； 滑模变结构控制； 反推法； 不确定项

现实中一些力学(机械)系统都可归结为非完整系统，如机器人、车载倒立摆、水下船舶及飞机起落架等一些带轮子的力学系统等。近年来，这一系统的研究得到了国内外研究者的广泛关注[1-9]，如：JIANG等[7]利用滑模变结构控制方法研究了一类非完整系统；王刚等[8]利用反推法研究了一类具有不确定项的非完整系统的指数镇定问题；MURRAY 等[9]研究了几类力学系统的反馈控制问题，但研究的系统较为理想化，未考虑实际力学系统中的不确定性因素(如系统中存在的未知结构参数、外界存在的干扰以及系统结构中存在的不确定性等)。因此，笔者以文献[9]的模型为基础，综合考虑系统中存在的不确定性因素，并运用文献[7-8]中的滑模变结构控制方法与反推法，对一类具有不确定项的非完整系统的反馈控制问题进行研究。

1 问题提出

考虑如下具有不确定项的非完整系统

(1)

假设1：对于任意的1≤i≤n-1，存在已知的非负函数ψi(t,x0,x1,…,xi,u0)，使得

(2)

成立。其中c0为正常数。

假设1表明:原点为系统(1)的平衡点。实际系统中很多的不确定因素满足该假设[4,7]。

2 反馈控制器设计

控制器设计过程中用到如下2个引理：

引理1[3]: 对于向量a,b，存在常数c，使得不等式

成立。

引理2[2]:对于任意的连续函数ψ(x1,x2,…,xn)，存在连续函数ψi(x1,x2,…,xn)(1≤i≤n)，使得等式

ψ(x1,x2,…,xn)=ψ(0,0,…,0)+

成立。

2.1反馈控制器u0的设计

为使系统(1)满足三角结构，对于(x0,v0)-子系统，采用滑模变结构控制方法。

取滑模面

S=v0+k0x0,k0>0。

(3)

S的导数满足

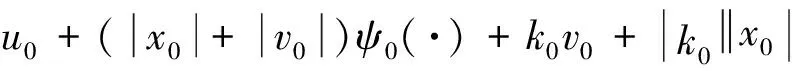
选取反馈控制器

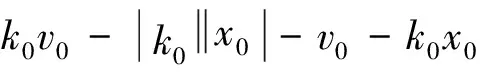
(4)

根据式(2)、(4)，可得

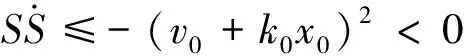
(5)

由式(5)可知：在式(4)的反馈控制器作用下，经过有限时间t，闭环系统的状态可到达滑模面S=0，且沿该滑模面到达原点，此时v0=-k0x0，且在该滑模面上有x0(t)≠0。

2.2反馈控制器u的设计

2.2.1 系统坐标转换

当初值x0(t0)≠0时，引入坐标-坐标转换

(6)

根据式(5)，式(1)中的x-子系统可转化为

(7)

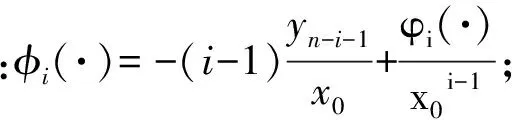
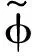
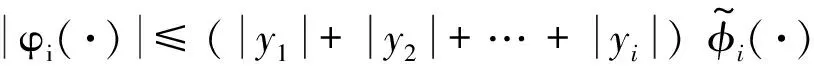
(8)

2.2.2 反馈控制器u的设计步骤

采用反推法对控制器u进行设计，其步骤如下：

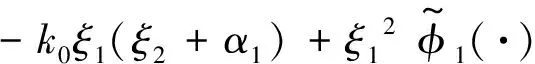
取虚拟控制函数

(9)

步骤i：假设在步骤i-1中，存在虚拟控制律αi-1和新变量ξi-1，使得

(10)

成立。式中：kj为待定的正常数。

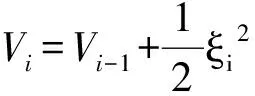
ξi+1=yi+1-αi(x0,y1,…,yi)，

(11)

根据式(8)、(10)，并对Vi求导，可得

k0ξi(ξi+1+αi)+Δi,

(12)

式中：

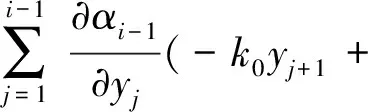
(13)

根据式(8)、引理1和引理2，存在光滑非负函数ωi(x0,y1,…,yi)，使得不等式

(14)

成立。由式(12)、(14)，可得

k0ξi(ξi+1+αi)+ξi2ωi(·)，

(15)

选取虚拟控制函数

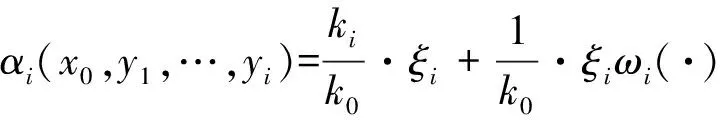
(16)

则有

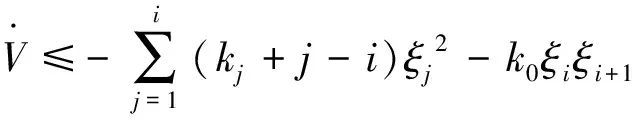
(17)

式中：ki为待定的正常数。

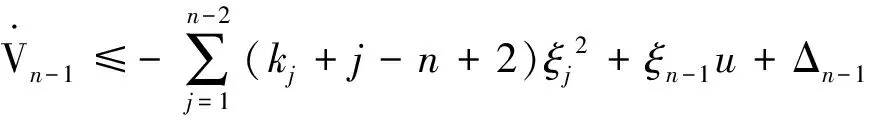
(18)

式中：

Δn-1=ξn-1[-k0ξn-2+φ1(·)-

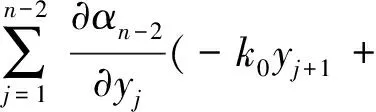
(19)

由完全平方公式可知：存在光滑非负函数ωn-1(x0,y1,…,yn-1)，使得

(20)

成立。选取反馈控制器

u=-kn-1ξn-1-ωn-1(·)ξn-1，

(21)

式中：kn-1为待定的正常数。

将式(21)代入式(18)，可得

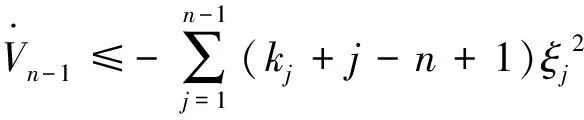
(22)

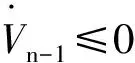
2.3稳定性定理

通过上述的滑模变结构控制方法和反推法，可以得到如下定理。

定理： 对于假设1，将设计的反馈控制器(4)、(21)应用于系统(1)，并通过选取合适的设计参数，可得闭环系统的状态是全局渐近稳定的。

3 仿真实例

考虑下列非完整系统

(23)

所研究的一般系统中的不确定项依次取下列函数φ0(·)=x0,φ00(·)=x02v0,φ1(·)=x02x1,φ2(·)=x2,并取初值x0(0)=1,x1(0)=0,x2(0)=1。

通过上述的反推法可得

(24)

图1 闭环系统的状态曲线

图2 闭环系统的控制输入曲线

闭环系统的状态曲线和控制输入曲线分别如图1、2所示。可以看出：闭环系统的状态曲线和控制输入曲线均以较快的速度趋向于0。仿真实例验证了本文结合滑模变结构控制方法与反推法所设计的反馈控制器对这类具有不确定性的非完整系统的有效性。

4 结论

针对一类非完整系统，在考虑系统具有的不确定因素的基础上，综合运用滑模变结构控制和反推法，设计了其反馈控制器，该控制器使得闭环系统的状态是全局渐近稳定的，仿真实例验证了笔者所提方法的有效性。所建模型能更好地反映系统的真实情况，属于非完整系统的一个新的研究方向，但仅对系统中存在的不确定性进行了研究，对于系统中存在时滞的情况，还有待于开展进一步研究。

[1] 胡终须，胡跃明，毛宗源.非完整移动机器人的分段反馈稳定控制[J]．控制理论与应用，2000，17(3)：358-362．

[2] JIANG Z P.Exponential regulation of nonholonomic systems with uncertainties[J].Automatica,2000,36(2):189-209.

[3] LIU Y G,ZHANG J F.Output-feedback adaptive stabilization control design for nonholonomic systems with strong nonlinear drifts[J].International journal of control,2005,78(7):474-490.

[4] XI Z,FENG G,JIANG Z P,et al.Output feedback exponential stabilization of uncertain chained systems[J].Journal of franklin institute,2007,344(1):36-37.

[5] LAFFERRIERE G A,SUSSMAN H J.A differential geometric approach to motion planning[M].Netherlands:Kluwer Academic Publisher,1993:235-270.

[6] 王朝立，霍伟.用滑动模态实现一类非完整动力学系统的指数镇定[J]．自动化学报，2000，26(2)：254-257．

[7] JIANG Z P.Exponential regulation of nonholonomic systems with uncertainties[J].Automatica,2000,36(2):189-209.

[8] 王刚，王朝立，赵晓萌，等．基于视觉伺服的非完整移动机器人镇定控制[J]．控制工程，2015，22(6)：1042-1046．

[9] MURRAY R,SASTRY S.Nonholonomic motion planning steering using sinusoids[J]．IEEE Trans.Automat.Control,1993,38(5):700-716.

(责任编辑: 尚菲菲)

ResearchonFeedbackControlforNonholonomicSystemsBasedonBacksteppingTechnique

JU Gui-ling1， LUO Jun-zhi1， YAO Jun-jie1， GU Juan1，LU Xing-hua2

(1. Department of Fundamental Courses, Academy of Armored Force Engineering, Beijing100072, China;2. Central Theater Command of PLA, Beijing100144, China)

This paper deals with the feedback control for the nonholonomic systems with uncertainties. In order to make the systems satisfy a triangularity condition, the state-state scaling is used. The sliding mode variable structure control and backstepping approach are used to design the feedback controller. The simulation results demonstrate the effectiveness of the proposed controller.

state-state transition; sliding variable structure control; backstepping; uncertainties

1672-1497(2017)04-0121-04

2017-03-13

鞠桂玲(1981-)，女，讲师，硕士。

O231.2

：ADOI：10.3969/j.issn.1672-1497.2017.04.023