产品质量控制:三步铸就卓越
2017-09-15俞钟行
产品质量控制:三步铸就卓越
给企业质量控制部门提供了增加有效管理的新机会。生产和技术管理部门为了支出费用最小化要求控制标注的近似值尽量接近最高允许值,而不冒常规险。这种工作模式要求决策者相信控制部门提供的数据及有关来源,向制订产品质量规则的管理者们提出了逐步法。该文作者为《产品质量控制》主编、技术科学博士奥列格•莫意西维奇•柔柴达尔。
测量控制;结果精确性;测量误差;统计分析
引言
三个问题:
问题1:控制点数的多少对判定是否达到相应的规范重要吗?
问题2:在回答第一个问题的基础上为完成生产工艺提供的资料足够可靠吗?
问题3:提供的资料在与消费者和外部控制机构进行建设性对话时足够可靠吗?
实际上,任何生产工艺过程的特性是不稳定的,它与设备状态、原料以及众多其他因素有关。正因为如此,要执行一成不变的安全与质量规范是有问题的。
正文
众所周知,企业经营者为了避免产品不合格往往提出比规定标准更高的要求,但这并不是消费者需要的。由此,产生资源额外消耗,产品竞争力下降。为了减少额外的消耗,必须保证测量结果控制的精准性。为此,需要付出相当的努力。
为降低消耗,在冒一定风险的情况下采取产品安全与质量指标尽量接近规范的极值。有必要进行以下说明:
1.根据控制结果判断,产品是否达到规范要求?
2.在完成生产任务的基础上,提供的资料能否使消耗降到最小?
3.与消费者和外部控制机构进行建设性对话时,提供的资料足够吗?
这就要求决策者具备一定的统计分析能力,熟悉国标гост р и с о9001-2015。后者是引用了另一个国标гост рисо/то 10017-2005。但是,该国标只是列举了现有的方法,没有与解决实际问题联系起来。因此,要回答上述问题采用按步骤解决的方法是有现实意义的。
第一步
为回答第一个问题提出一个简单的算法。
如果监控的测量值有效地记录了达到(或违背)规定的要求,则判断产品的质量不会引起疑问。但是,在不可预知的情况下出现了监控值的反复变化。这时就难以判断产品究竟是达标还是没有达标。当企业力争最大限度接近规范值时,这种可能性出现的频率会增大,这种情况下可采取不确定条件下的理论来回答上述问题[1]。为说明该理论的应用可举出具体的例子。
实例1 在叶卡捷琳堡战争中伤残者居住的医院中,蒸馏水中铅浓度的检测值参见图1。如果规定,铅浓度的上限为50微克/立方分米,由图1看出,部分检测值达到了铅浓度的上限。那么,这样的蒸馏水符合规范吗?
解决方案 取决于被授权人能承担风险性的大小,有以下几种情况:
1.1蒸馏水中铅浓度测试的平均值为27.5微克/立方分米,(在图1a是下面的水平线)低于最高允许浓度。因此可认为铅含量是正常的,这个结论是从所谓的最高准则出发,而不考虑可能的,也许是很少的产品质量不达标。
1.2相反,瓦列达最大最小准则将使有悲观情绪的决策者关注所获得的测控结果的最差值,见图1a上第4点,此处铅浓度高达173微克/立方分米,对应图中上面的水平线,它远远高出标准极限值,说明产品不合格。
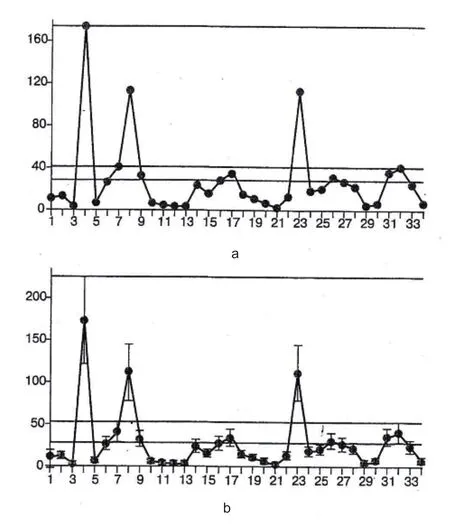
图1
1.3在折中的情况下根据赛维特莎最小最大准则对在最坏的情况下可能造成的最少损失进行评估。我们去除曲线中几个极端高的数值,如4、9和24点,在这种处置下,相对高的数值变成了第7点,相当于40.6微克/立方分米(图1a中间水平线)这个铅浓度低于标准极限值。
可见,根据监控结果来评定产品质量有多种方式。它们取决于决策者对要解决任务的了解和责任大小。例如,为了确保产品更高的安全性要采取最高准则,尽管在其他情况下可能采取更宽容的要求。
上述逐一举出的解决方案的不完备之处,在于没有考虑到测试工具会不可避免地带来测试误差。尽管测试工具正式通过了“行政决议接受”,但在实际完成任务中误差是很高的,达到±30%,有时还要高(见例2)。因此,在实际操作中测试结果不是取瞬间值,而是取在一个区间中的数值。(图1b)考虑到测量误差,只保留最高值。原有的高值和低值分别提高到225.5和53.2微克/立方分米,如图1b中三条水平线所示,并与图1a中三条线相对应。可见,前面提到的蒸馏水按最小准则合格的判断现在变成不合格了。
评论 可以通过提高测试装置和方法的精度或者重复测试来降低误差率,这当然会增加额外支出,需要决策者根据生产和市场情况来决定。这种想法曾经计划通过实验来验证,可惜在国标гост рисо 9001-2015中未加考虑,仅仅提及了分析和评价在监控和测量过程中获得的相应数据和信息的必要性。要回答测试结果是否有足够可信度的第二个问题需要进行有计划的工作。
第二步
设计这样一个实验。实验中规定控制的精度既不是过度的,导致浪费;又不是不足的,造成损坏。通过上面提到的战时医院净水供应的例子来了解这个实验方法。
实例2 要求通过减少监控机构由于测量误差而作出的错误鉴定来提升净水生产管理的效率。假设规定误差为±40%,企业的收益与一次测量费用之间的关系为:物理疗法用水30、公共饮食50、注射剂用100、血液用150,净水中污染物为中等浓度——0.95п д к(浓度极限值)。
解决方案 重复检测是降低误差最简单的办法。但是要考虑到检测费用会随着检测次数增加而上升,而误差减少仅与检查次数的平方成比例。所以,降低作出水质量错误结论的风险将会减少企业收益。根据上述讨论可进行简单的计算,其结果见图2。由图可见,对于纯水不同的用途,重复检测的次数也大不相同:物理疗法用水为1,公共饮食为3,注射剂为11,血液为24。这时,第一种用途水质量的误差将保持在40%左右,而后面三种用途水质量误差分别降到23%,12%和8%。从图2a、b、c、d可看出三根曲线都有最高点,说明若要符合国标го с т р и с о 9001无限提高消费者对水质量的满意度而过度检测将造成很大的浪费。检测精度不够当然是有害的,为外乌拉尔北部地区的注射剂和血液提供有危险的水的事件就是一个实例。
注解 上面提到的测量误差±40%是在满意的概率0.95下确定的。所以,真实的测量值中只有95%其误差在-0.4到+0.4范围内,而剩下的5%的误差不在此范围中。当然可以确定比0.95更高的概率。但此时将扩大误差范围,如果缩小误差范围,则会提高控制错误的概率,结果得到的是正如俄罗斯联邦工业和贸易部前副部长萨拉玛德夫所说“非此即彼”。通常抽样检测引起的错误结论带来额外的危险,使产品质量变得不稳定。抽样检测是经济的,但不能保证结果的可靠性,图1样品不是每天检测一次,图3样品每天检测一次,水中铅浓度的平均值为16.1和27.55微克/立方分米。通过“最大最小”和“最小最大”两个准则换算,将得到53和35微克/立方分米,替代以前的225.5和53.2微克/立方分米。这样,产品不合格的结论就要重新考虑了。分析表明,在抽样控制错误和测量误差的两倍相等的条件下可实现水质量的最佳控制。因此,如果测量值超过抽样控制错误的一半就要设法加以降低。如果做不到,就要限定抽样的容量。
图3显示:从图1每天测试结果中每隔1天挑选数据,构成此图时,“缺”的那天铅浓度等于上一天的数值。
有趣的后果 在完成规范“严厉的”或“宽松的”条件下可得出完全相反的结论。例如,在限制产品中有毒物质含量时可要求浓度с<пдк(浓度极限值)或с≤пдк。下面让我们来看一下。
例3 生牛奶中锆的浓度极限值为6微克/升。无论执行严厉的规范或宽松的规范都要根据仪器控制31个样品的结果来讨论(见图4)。设锆的平均浓度为C=6.95微克/升(图4中水平实线),样品中浓度的不稳定值(二次偏差的平均)σ=3.45微克/升,那么在概率为0.95的条件下u=1.64(正态分布下的列表数值)。
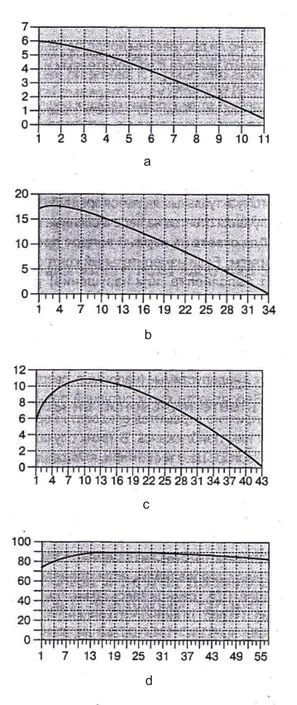
图2
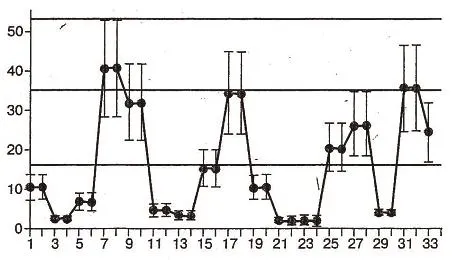
图3
解决方案 在“宽松”限制下,公差值应扩大,即σ•u=3.45×1.64=5.66(对应图4中上部虚线),可见,31个样品中有30个合格。而在“严厉”限制下,得出相反的结论,31个样品中只有2个合格(见图4中下部虚线)。
大熊代表的生物才是自然界真正的主人。这种认知是随着人类品尝过现代工业文明带来的副作用的苦涩果实之后才被人类重视并逐渐接受的。福克纳笔下大熊和山姆这两个代表了自然和谐的形象在文中的时代是注定要被现代工业文明所消亡的。在《熊》中,福克纳极具预见性地警告了读者:森林的消亡与大自然的损害必将带来人类无法挽救的恶果,人类终将自食恶果。《熊》强烈批判了盲目自大而无节制的人类文明其毁灭性和邪恶性的一面,并为后世的文学艺术创作提供了新鲜而深刻的话题—人类在与自然的互动中所处的关系是从属关系、人类必须要遵循自然规律与大自然和谐相处。
所以,取决于上级组织对产品质量的负责程度,可以降低或者提高要求。
上面讨论中还没有涉及到消费者或外部监控机构(国家层面的,社会的)对产品质量及其安全性是否认可。为了确立证明材料的充分有效,必须对产品质量进行有分寸的监控。第三步就是来完成此目的。
第三步
第三步是在产品质量监控帮助下,沿着生产的经济有效性途径,不计较在分析上要稍微复杂些,为了完成规定的要求,将监控指标从置信区转换成所谓的可容忍区。考虑到监控有可能不可靠和限制不合格产品流出的风险程度,采取“极限转换”是有必要的[2]。
当有50%甚至90%不合格产品时很容易确定没达到规定的要求,如果不合格产品只有5%甚至更少,这时会被忽视。为了不发生这种情况,必须确立一个可能性范围。在此范围中产品不合格的风险处于可接受的程度。如果这个可容忍区域的上限低于产品合格的允许概率,那么产品就被淘汰了。如果容忍区的下限高出合格的允许概率,产品是可以被接受的,下面用实例加以说明。
实例4 设规定要求的完成概率为90%以上,如果在取样中发现(甲)1个,(乙)5个,(丙)10个样品不合格,请评估为符合规定要求必须的测试次数。
解决方案 利用统计表很容易得到所需的结果,例如,这里完全适合用二项分布的统计数表,找到上面案例条件下的答案:
(乙)相应的测量次数分别为20次和100次。
(丙)相应的测量次数分别为60次和150次。
可见,为了获得产品许可必须测量的次数比排除产品合格测量的次数多得多。因此,节约监控抽样的数量将会增加作出错误结论的风险。在依据降低测量资讯不确定程度时要考虑到排除产品合格的次数愈少,则测量的次数愈多。换言之,质量水平愈高,监控的容量也就愈大。甚至在测量中没有发现不符合要求,并不意味着产品就一定合格,规则“如果未查到不符合,则满足规定的要求”完全不等同于规则“如果达到要求了,则不存在废品”对产品的信任是由后面的一个法则来保障的,因此需要进行大量的监测,这样才能更好地保证产品的质量和安全性。
结论 量子力学奠基人薛定谔认为,无论描述任何东西,都离不开数学的帮助[3]。如果不用数学,我们能通过统计法控制产品质量来有效提高生产管理吗?显然是不能的。
根据不同的资料,对产品进行质量监控的投入占生产成本的5%~50%。这是一个不小的数字。因此要通过优化监控服务工作获得可靠的资讯来保证企业最大的收益。
应用提议的管理方法,可以节约资源而无过多的生产风险。
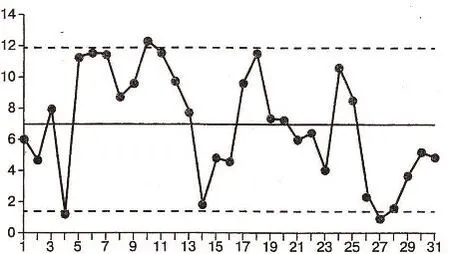
图4
来自作者的话
为了用文中建议的方法,推进提升管理的有效性,《产品质量控制》杂志联合《标准与质量》杂志,向各组织的领导、经理、大学生及所有感兴趣的人推荐研究这篇“三步致胜”的文章。
(1)考虑一下,你们在自己的生产中,在不确定的条件下,根据现有的监控服务,采用什么方法来决定产品符合/不符合规定要求的?如最大最大法、最大最小法、最小最大法等。
(2)要可靠地根据所获数据,作出内部生产是否合格的判定,就必须向优化工作程序的监控部门清晰地表明自己的任务。
(3)必须明白,在与顾客及外部监督组织进行建设性对话时,所有的资讯是充足够用的吗?有必要再次优化测量监控的程序。
《产品质量控制》杂志希望用控制的方法,促进国家产业的发展,开启卓越中心以推动“三步致胜”的程序。程序参加者可优惠订阅《产品质量控制》杂志,并获得卓越中心委员会的荣誉称号。
做到第1步获得黄带称号技师;做到第2步获得绿带称号技师;经挑选后实施全部三个步骤者,将认为具有高技能水平,拥有荣誉证书获得黑带技师称号。在你们走向成功的道路上,请阅读《产品质量控制》杂志原文吧。
[1]芭拉诺夫 B.B .利益趋动的管理决策过程 [J].数理学刊,2005,p296.
[2]柔柴达尔 O.M.新方法必要性和实质的评价:物体及物质的组成和性质,在利益上稳定发展的化学[J].2015,23卷,5期,p539-542.
[3]薛定谔.什么是生活 [M]. IIL,1947,P150.
(俞钟行 译 余志洪 校)
