超大跨斜拉悬索协作体系桥参数优化设计研究
2017-09-15谢宏伟蒲黔辉李世伟
谢宏伟, 蒲黔辉, 李世伟
(西南交通大学桥梁工程系,四川成都 610031)
超大跨斜拉悬索协作体系桥参数优化设计研究
谢宏伟, 蒲黔辉, 李世伟
(西南交通大学桥梁工程系,四川成都 610031)
斜拉悬索协作体系桥吸收了斜拉桥和悬索桥的优点,是超大跨度跨海工程的优先选择。文章以巽他海峡地质、地貌条件为基础,介绍了超大跨度斜拉悬索协作体系桥的方案设计,并采用有限元分析软件,研究了体系关键参数交叉吊索数量对端吊索轴力、桥梁刚度、材料用量以及自振特性的影响。相关结论可以为类似桥梁的研究和优化设计提供参考。
巽他海峡; 超大跨度; 斜拉悬索协作体系; 交叉吊索; 有限元分析
1 工程背景
巽他海峡是印度尼西亚爪哇岛与苏门答腊岛之间的狭窄水道,长120 km,宽22~110 km,最大水深1 080 m。苏门答腊岛和爪哇岛虽说是印度尼西亚人口最稠密、经济最发达的地区,但长期受海峡影响,两岛之间联络现在仍靠轮渡,单程需要4 h,高峰期排队汽车延绵达10 km,交通十分不便。
拟建桥梁位于繁忙的国际航海通道,不仅要满足客货轮的航行,还需允许军事舰船的通过。基于以上舰船通航宽度的要求,要求桥梁主跨至少2 200 m,满足目前世界上最大舰船能够单向航道自由通过桥跨,或双向航道受管制通过桥跨,桥下净空要求85 m,该净空考虑了今后全球气候变暖导致的海平面上升、海啸等因素。根据拟建桥梁所处位置的海床地形,将纵桥向两锚锭间距离定为3 800 m,桥跨布置条件示意如图1所示。

图1 桥跨布置条件示意
2 桥型比选
缆索受力体系是超大跨径桥梁的必然选择,采用缆索结构的桥型主要有斜拉桥、悬索桥以及斜拉悬索协作体系桥。根据中国目前已建缆索承重桥梁的材料用量和造价,经过理论推导,在一定条件下,从单位桥面面积造价的角度来说,跨径超过1 200 m时,斜拉桥与岸上锚碇悬索桥相比不具优势;跨径超过1 600 m时,斜拉桥与水中锚碇悬索桥相比不具优势[1]。巽他海峡大桥跨径在2 200 m以上,只能采用地锚式悬索桥或斜拉悬索协作体系桥。
悬索桥虽具有较强的跨越能力,但随着跨径进一步增大,将逐渐面临着另外一些问题:(1)可能存在着比斜拉桥更为严重的风致振动稳定性问题;(2)当需要在深水区修建基础或锚碇时,施工难度及费用剧增,而当桥梁跨度在2 000~5 000 m内时,深水基础和上部结构成本决定了经济跨度[2]。
相比悬索桥,斜拉悬索协作体系桥可以减少锚碇规模,大大减少在海中修建锚碇的造价和风险,尤其对常常面临深水和软土地基条件的跨海大桥意义重大;静力方面,借助与斜拉体系的协作,可以提高悬索体系的刚度;动力方面,中跨跨中部分采用悬索体系,可以解决斜拉体系在悬拼过程中的气动稳定和主梁压力过大的问题[3]。
3 方案设计
初步设计中,考虑通航净空要求、桥位地质条件、结构造价低、抗风性能好、结构美观新颖、受力合理以及城市整体规划等设计要求,并结合已建同类桥梁的经验,拟定方案的主要构件尺寸(图2)。
3.1 总体布置
巽他海峡大桥主通航孔拟采用公铁合建双索面斜拉悬索协作体系桥,线路设计为双向6车道。结合已建同类桥梁经验,主缆矢跨比为1/9,横桥向间距52 m,加劲梁宽54.8 m,含人行道总宽57.8 m,桥跨布置为(800 +2 200+800) m,边、中跨比为0.36。
3.2 主梁
采用流线形分离三钢箱加劲梁,纵向箱梁高3.0 m,纵向箱梁在顺桥向每隔30 m采用箱形横梁连接,横梁宽3 m,高4.5 m,吊杆设在横梁端。加劲梁两侧设置风嘴,外挑1.5 m,人行道板兼作风场导流板。两边箱供公路使用,中间箱梁供双线铁路,边箱梁与中箱梁间间隙3.7 m,形成分离三箱通风格栅。

(a) 桥跨布置(立面)
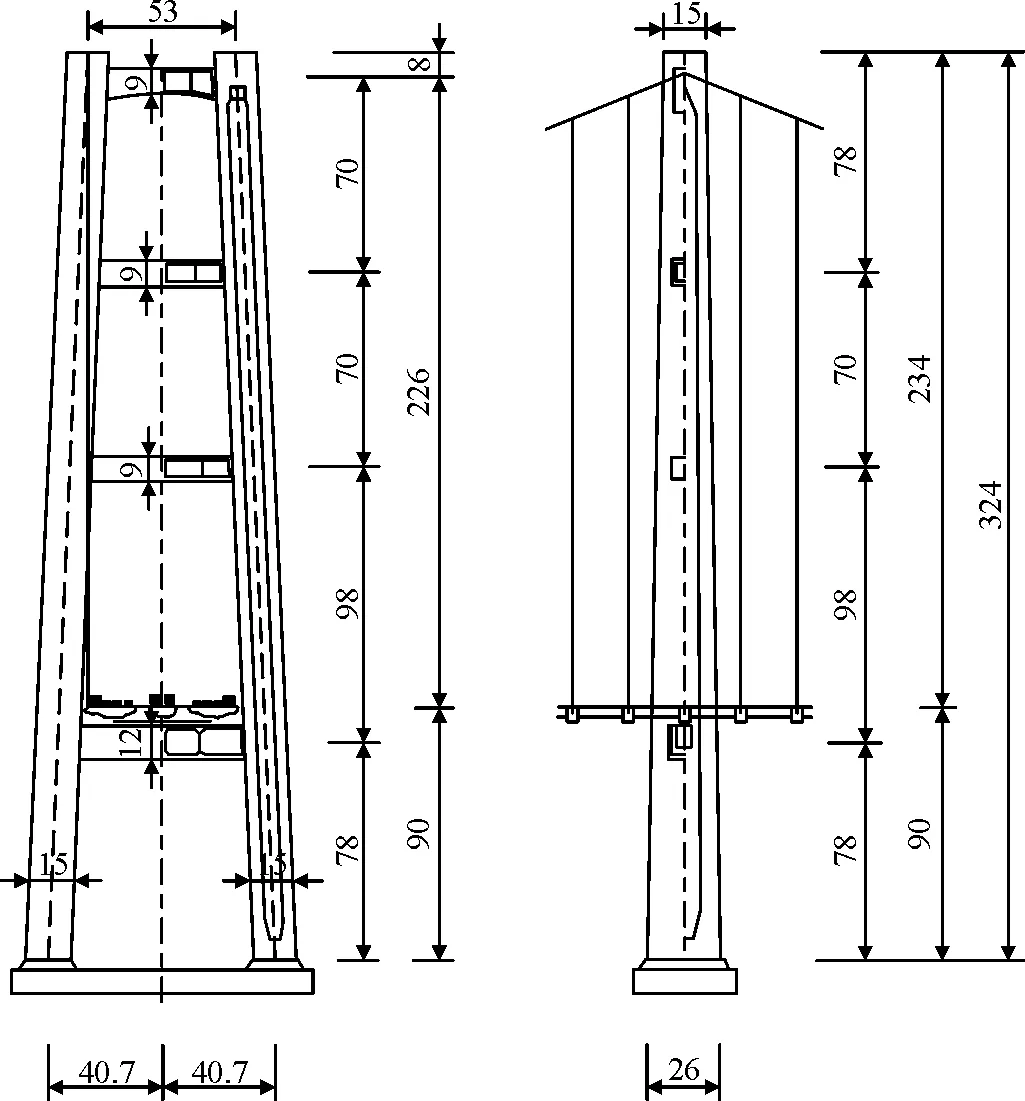
(b) 桥塔(正立面) (c) 桥塔(侧立面)

(d) 主梁(横截面)

(e) 单侧双主缆(横截面)图2 方案的主要构件尺寸布置(单位:m)
3.3 桥塔
采用刚构式钢塔,设置4道横梁,塔柱截面横桥向宽14 m,纵桥向宽塔顶14 m渐变到塔底18 m,为减少近海面海洋环境对钢结构的腐蚀,塔底采用混凝土结构。塔柱截面外形需要根据截面气动力特征确定。
3.4 缆索体系
主缆通长布置,单侧2根,全桥共4根主缆,主缆采用镀锌高强平行钢丝,Ep=2.0×105MPa,fpk=1 770 MPa,采用PPW法架设。吊索采用双吊索形式,PES7-241平行钢丝束,材料采用8×55SW+IWR、8×41SW+IWR镀锌钢丝绳,公称抗拉强度1 860 MPa。
4 参数分析
4.1 计算模型
根据设计方案的尺寸,利用有限元软件建立全桥模型,主缆及吊杆采用索单元模拟;主梁、横梁和桥塔采用梁单元模拟;加劲梁在右侧桥塔处纵向自由度自由,面内弯曲自由度释放;加劲梁在左侧桥塔处纵向自由度约束,面内弯曲自由度释放;成桥阶段主缆与桥塔固结;按双向6车道公路和两线敞车-80车荷载计算,同时考虑铁路行车有重载方向的特点,列车加载长度为700 m。
4.2 参数描述
任何桥梁结构在活载作用下,当构件的应力幅大于材料耐久极限时,将产生疲劳问题,而斜拉悬索协作体系在斜拉索和吊索结合部位,刚度变化大,在活载作用下,端吊索产生较大的应力幅,易出现疲劳问题。使斜拉索与吊索交叉(图3),可以将活载最大交变轴力区在更大的区域内分布,对降低两端吊索的活载应力幅十分有利[4]。
以交叉吊索数N为参数,分析端吊索和边斜拉索传力效率,模型如图4所示。

图3 交叉吊索示意
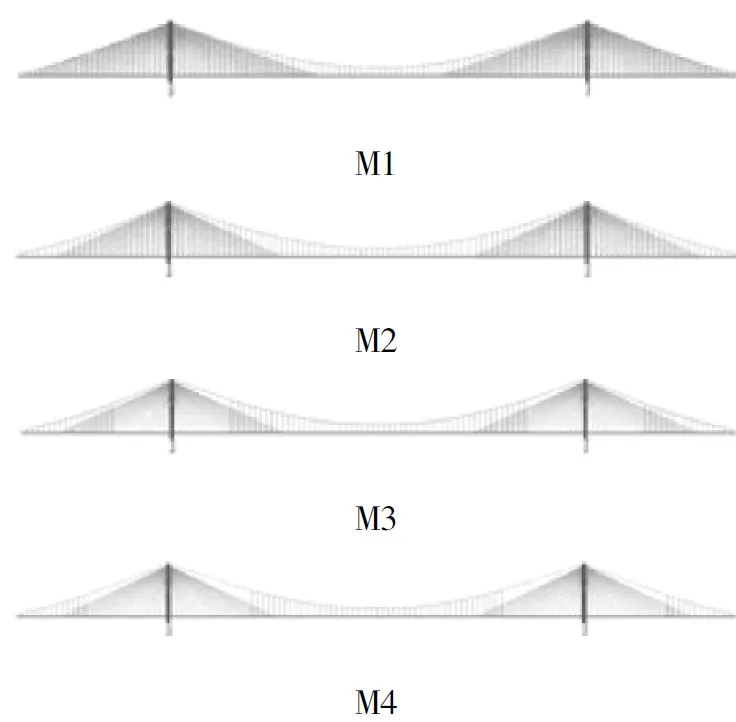
图4 分析模型
建立模型M1,吊索与斜拉索满布(N=26),分析得出边斜拉索索力,其中最大为1 125 t ,长度为812 m,倾角正弦为0.33,传力效率较低;去掉两侧索力大于1 000 t的斜拉索后形成模型M2(N=20),分析得出塔墩附近吊索受力较小,最小为393 t ,长度为278 m;去掉后形成模型M3(N=10);再调整参数形成模型M4(N=5)。考虑以上四种情况(N=26、N=20、N=10、N=5),进一步分析研究参数的影响。
3.3 参数N影响分析
分析比较不同交叉吊索数量下桥梁的力学行为,共考虑四种情况:N=26、N=20、N=10、N=5。根据已建造的超大跨度公铁斜拉悬索协作体系桥梁的工程经验并考虑一定的安全度,在分析过程中改变主缆直径使得主缆安全系数相当(2.3±0.1)(表1)。
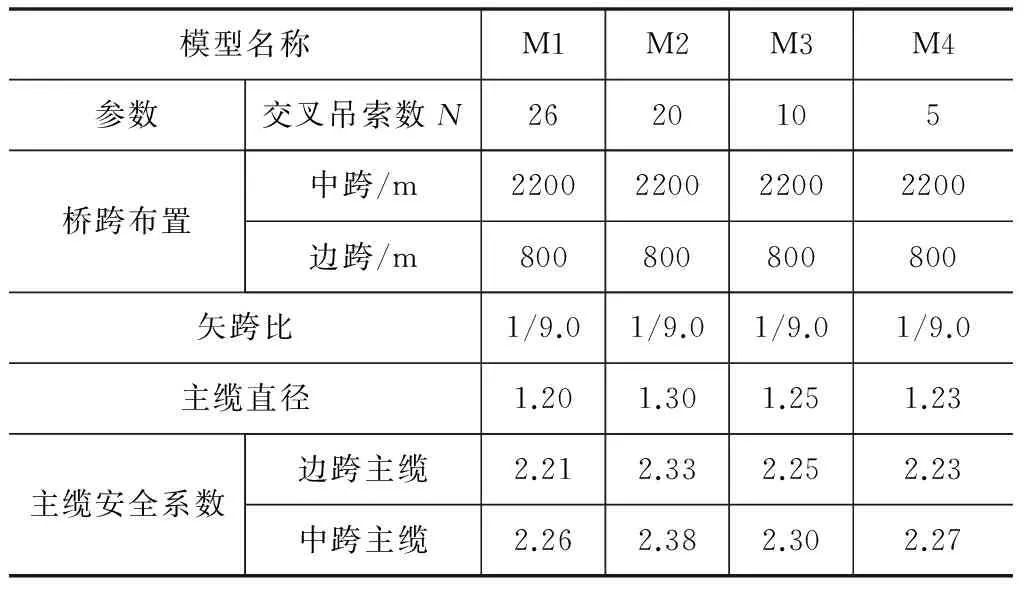
表1 主缆直径和安全系数
4.3.1 参数N对刚度的影响
通过交叉吊索数量的变化,挠跨比、梁端转角以及塔顶位移的计算结果如表2所示。不同的交叉吊索数量对挠跨比、梁端转角以及塔顶位移的影响情况分别如图5~图7所示。
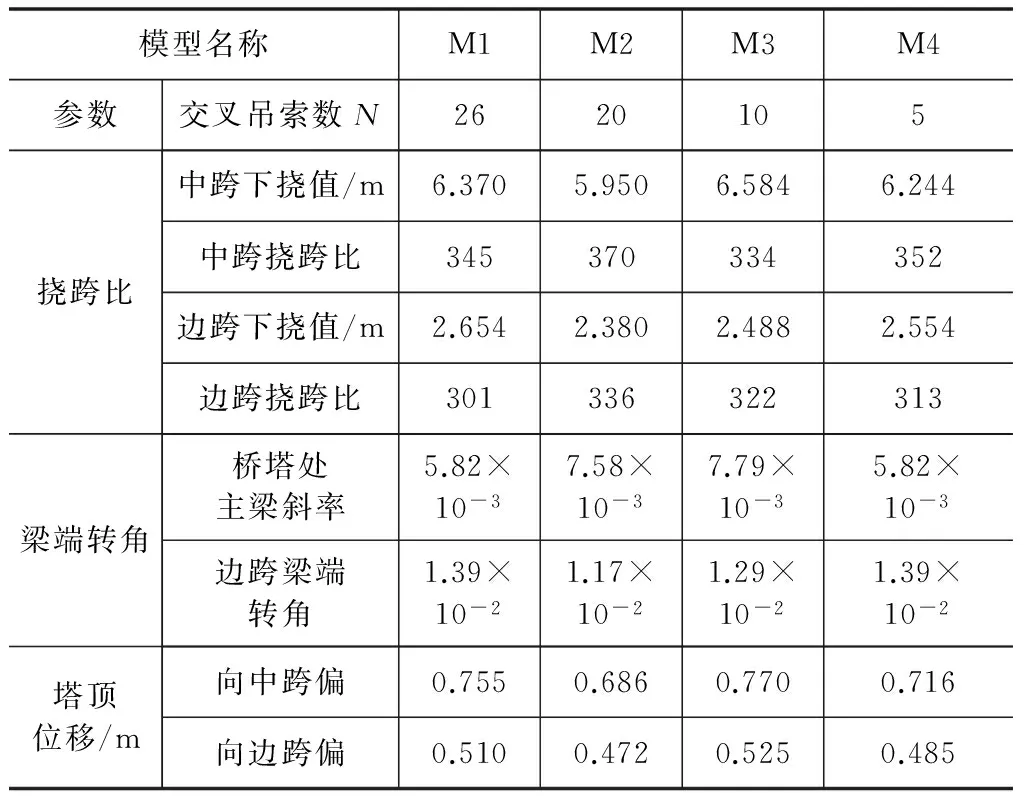
表2 参数N对刚度的影响

图5 参数N对挠度比的影响

图6 参数N对梁端转角的影响
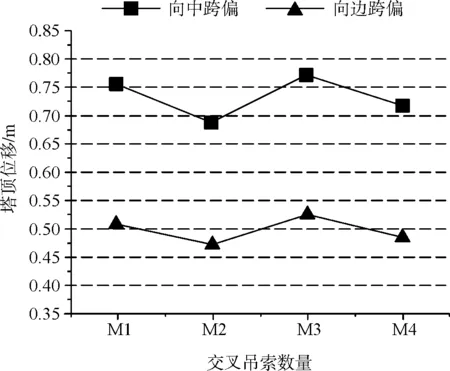
图7 参数N对塔顶位移的影响
可知在保持主缆安全系数相当的前提下,有以下结论成立:
(1)随着交叉吊索数量N的减少,边中跨挠跨比均呈非线性变化。当N=20 时,边中跨的挠跨比均达到最小,表明此时斜拉悬索协作体系桥刚度较大。以上四种计算模型边中跨挠跨比均满足小于1/300的条件。
(2)桥塔处主梁斜率和边跨两端转角对交叉吊索数量N的变化并不敏感,标准差分别为1.87×10-3、1.81×10-3,且边跨梁端转角均满足小于0.02 rad的条件。
(3)向中跨塔偏和向边跨塔偏随交叉吊索数量N的变化趋势相同,其中向中跨塔偏最大为0.770 m,向边跨塔偏最大为0.525 m。在桥塔应力满足规范要求的前提下,应对主缆在索鞍内的滑移进行验算,并采取有效措施使其满足规范要求。
4.3.2 参数N对材料用量的影响
通过交叉吊索数量的变化,主缆、斜拉索、吊索以及桥面以上桥塔用钢量的计算结果见表3。不同的交叉吊索数量对用钢量以及用钢量总价的影响情况分别如图8~图9所示。
可知在保持主缆安全系数相当的前提下,有以下结论成立:随着交叉吊索数量N的减少,斜拉索和吊索用钢量均呈递减趋势。为了保持主缆安全系数相当,主缆直径存在变化,其用钢量在N=26时取最小,N=5其次,N=20 时达到最大;用钢量总价随参数N的变化趋势与主缆用钢量随参数N的变化趋势一致,即就材料用量与总价而言,主缆直径起主要控制作用,在满足主缆安全系数的要求下,宜减少主缆直径。
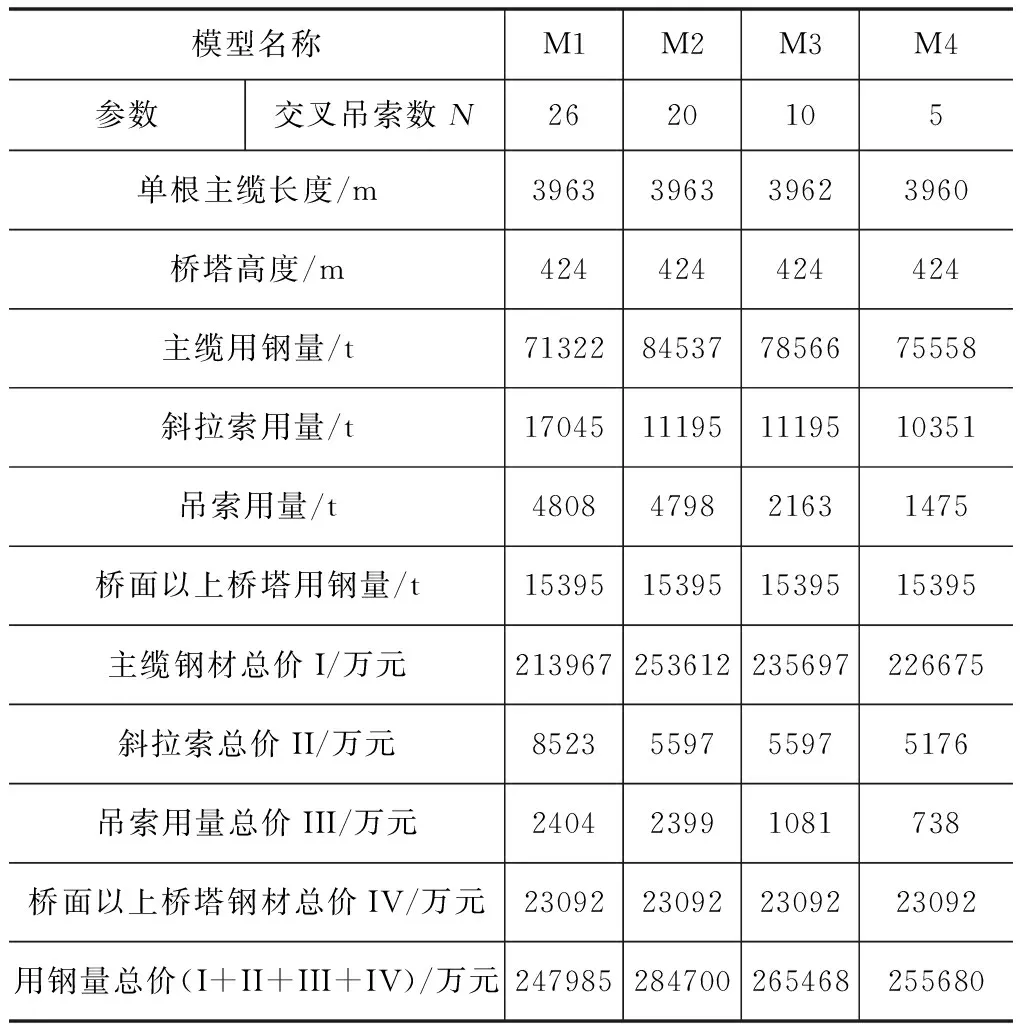
表3 参数N对材料用量的影响

图8 参数N对用钢量的影响
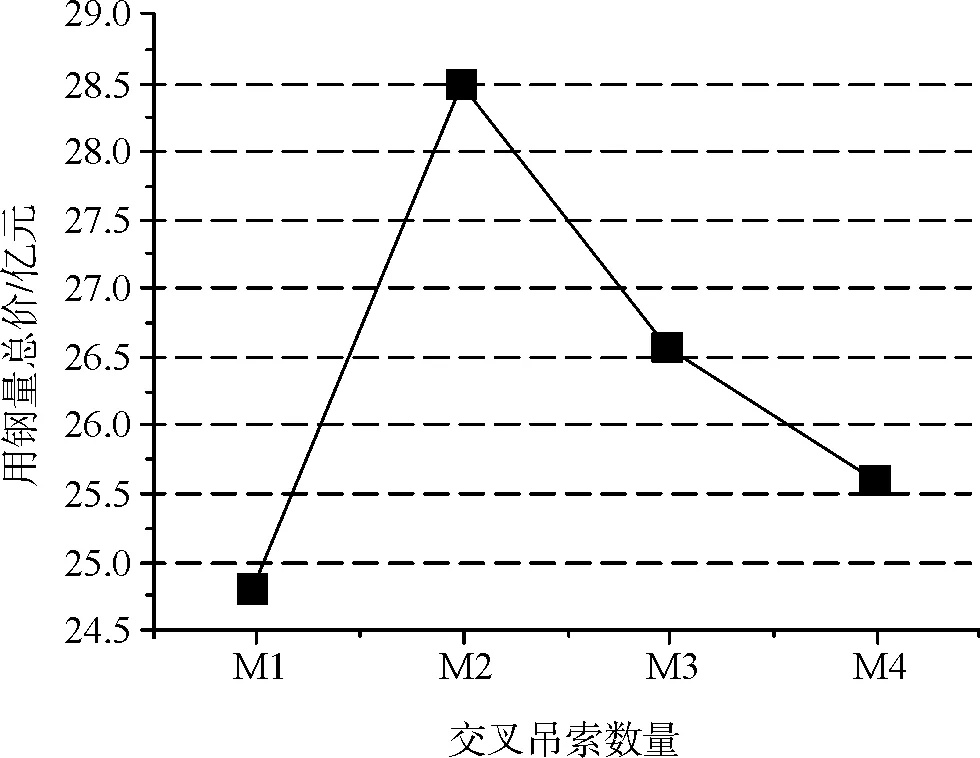
图9 参数N对用钢量总价的影响
4.3.3 参数N对自振特性的影响
反映桥梁动力特性的重要振型为主梁的一阶竖弯、一阶横弯与一阶扭转[5]。通过交叉吊索数量的变化,斜拉悬索协作体系桥自振特性的计算结果见表4。
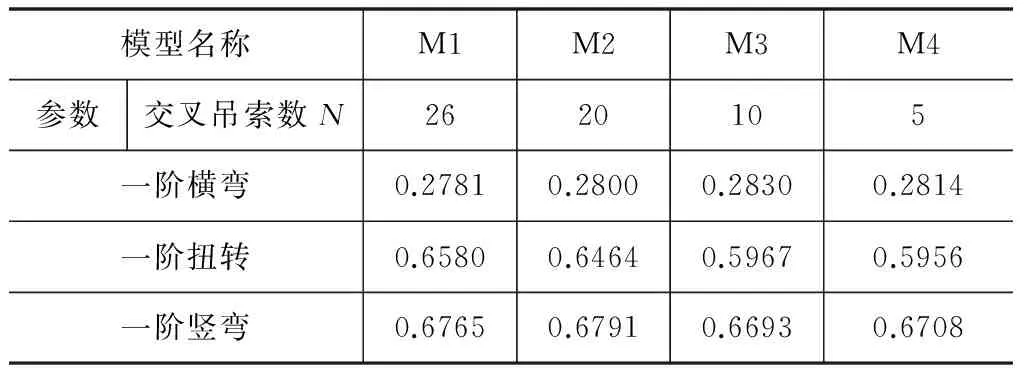
表4 参数N对自振特性的影响
可知在保持主缆安全系数相当的前提下,有以下结论成立:
斜拉悬索协作体系桥的交叉吊索数量对其自振特性影响并不大;在以上四个模型中,一阶扭转频率变化并不敏感,标准差为0.056 65,表明缆索体系、塔、梁共同参振,共同分担主梁从来流中吸收的能量的程度比较接近。
5 结论
本文以巽他海峡斜拉悬索协作体系桥结构体系为背景,采用有限元计算手段,在通过改变主缆直径,保持主缆安全系数相当的前提下,研究了挠跨比、梁端转角、塔顶位移、用钢量以及自振特性对参数交叉吊索数量的敏感性。针对巽他海峡斜拉悬索协作体系桥结构体系,得出了以下结论:
(1)边中跨挠跨比随交叉吊索数量呈非线性变化。当交叉吊索数量为20时,挠跨比最小,且均满足小于1/300的条件,交叉长度与主跨比在5.5 %~34 %;主梁斜率和边跨两端转角对交叉吊索数量的变化不敏感,边跨梁端转角均满足小于0.02 rad的条件;随着活载布置位置的不同,塔顶向中跨偏大于向边跨偏,在桥塔应力满足规范要求的前提下,应对主缆在索鞍内的滑移进行验算,并采取有效措施使其满足规范要求。
(2)随着交叉吊索数量N的减少,斜拉索和吊索用钢量均呈递减趋势,主缆用钢量先增加后减少,且用钢量总价随参数N的变化趋势与主缆用钢量随参数N的变化趋势一致;就材料用量与总价而言,主缆直径起主要控制作用,在满足主缆安全系数的要求下,宜减少主缆直径。
(3)斜拉悬索协作体系桥的交叉吊索数量对其自振特性影响不大;缆索体系、塔、梁共同参振,共同分担主梁从来流中吸收的能量的程度比较接近。
[1] 肖汝诚, 姜洋, 项海帆. 缆索承重桥的体系比选[J]. 同济大学学报: 自然科学版, 2013(2): 179-185.
[2] 郑凯峰, 胥润东. 琼州海峡超大跨度公铁两用悬索桥方案的提出和初步研究[J]. 钢结构, 2009(5): 28-32.
[3] 肖汝诚. 桥梁结构体系[M]. 北京: 人民交通出版社, 2013.
[4] 肖汝诚, 贾丽君, 薛二乐, 等. 斜拉-悬吊协作体系的设计探索[J]. 土木工程学报, 2000(5): 46-51.
[5] 张哲, 王会利, 黄才良, 等. 自锚式斜拉-悬索协作体系桥梁设计与分析[J]. 公路, 2006(7): 44-48.
谢宏伟(1994~),男,在读硕士研究生,研究方向为大跨度预应力混凝土桥结构行为;蒲黔辉(1965~),男,工学博士,教授,研究方向为大跨度预应力混凝土桥结构行为、桥梁结构行为研究与评估;李世伟(1987~),男,在读博士研究生,研究方向为大跨度预应力混凝土桥结构行为。
U448.25
A
[定稿日期]2017-04-14
