博弈论视角下学生评优工作中的投诉问题的管理对策

(温州医科大学眼视光与生物医学工程学院 浙江 温州 325035)

博弈论视角下学生评优工作中的投诉问题的管理对策

常笑张海锋

(温州医科大学眼视光与生物医学工程学院浙江温州325035)

通过分析高校学生评优中存在的问题，提出了学生投诉中存在的博弈基础，构建了投诉博弈模型，求出模型的纳什均衡解，并对均衡解的影响因素进行分析，最后给出高校管理对处理投诉问题的政策建议。

博弈论；学生工作；投诉；对策

1967年美国乔治·梅森大学Gordon Tullock提出寻租理论的思想，1974年美国经济学家Anne Krueger建立了寻租理论，1988年我国吴敬琏教授等率先在《经济社会体制比较》杂志上介绍寻租理论，国内的许多学者从不同角度进行了管理分析[1,2,3]。寻租理论的提出，将经济学家研究的视野从生产性的寻利活动扩展到了非生产的寻租活动，把人们追求新增经济利益的行为和追求既得经济利益的行为区分开来[1]。根据寻租理论的思想，管理部门运用行政权力对被管理者的收益活动进行干预和管制，妨碍了自由竞争的作用，从而创造了少数有特权者取得超额收益的机会。这种超额收益被称为“租”(rent)，谋求这种权力以获得租金的活动，被称作“寻租”，因此，寻租是与特权相伴而生的，而委托代理关系的存在又是产生特殊权力的根本原因[4]。

博弈论(Game Theory)研究的是决策主体间行为发生直接相互作用时的决策以及这种决策的均衡问题。通过文献检索，目前很少有学者以高校学生工作中的投诉为模型建立相关博弈分析，本文通过构建投诉博弈模型，求出模型的纳什均衡解，并对均衡解的影响因素进行分析，最终给出治理高校评奖评优过程中投诉问题的对策建议。

一、高校学生工作评优中的投诉问题分析

随着反腐及法制化建设的推进，高校学生的维权意识也逐渐提高[5]。高校学生工作中，评优作为树立典型，引领学生工作前进的重要抓手，越来越受到教育管理部门的青睐。高等教育的普及，使得高校毕业生就业竞争越来越激烈，用人单位在选人用人时也会以学生是否为中共党员或者在校期间获得哪些先进荣誉等为重要参考，另外国家奖学金等一些优秀奖学金金额较高，与利益挂钩的奖项向来是学生较为关切的，稍有不慎就会导致一些学生的不满，高校的发展以安全稳定为第一要务，监管部门在学生比较关切的敏感问题上，一直处于高度关注状态。以浙江省温州市某高校为例，该校自2011年以来，在历次研究生先进评选中，发生投诉10例，其中匿名投诉8例。

投诉是一方对于评判结果不满意时，向上级监督管理部门提出异议的一种方式。投诉的发生有二种方式，一是管理部门权利寻租，使得评选结果有失公允，学生利益相关者不满结果，发生投诉；二是管理部门在公开公平的情况下，因为信息不对称，一些学生对于管理者或者获奖者存在异议，在未核实的前提下，向相关部门提出质疑。本研究构建的投诉模型是基于以上两种假定情况。

二、高校学生工作中评奖评优的投诉博弈模型构建

(一)博弈模型假定

假设高校评奖评优中的学生投诉活动涉及三个参与者：投诉人、管理部门、监督部门。投诉人有两种策略：投诉和不投诉。监督部门也有两种策略：监督和不监督。投诉人的投诉概率为p，投诉人的正常支付为v，这个正常支付就是投诉人在不投诉情况下的正常的获益值，当投诉人投诉成功后，投诉人获得额外的投诉收益Δv，为此投诉人为了投诉所带来的负面影响及产生不良后果的效益值为αΔv(0<α<1)，αΔv就是投诉人的投诉成本；管理部门的正常支付为s，被投诉产生的影响效益值为g；监督部门的监督成本为c，监督概率为q，监督成功的概率为u；投诉行为成功后，监督部门的收益为m，并对管理部门进行惩罚为n。所有变量取值均大于0，三方博弈支付模型如表1所示：

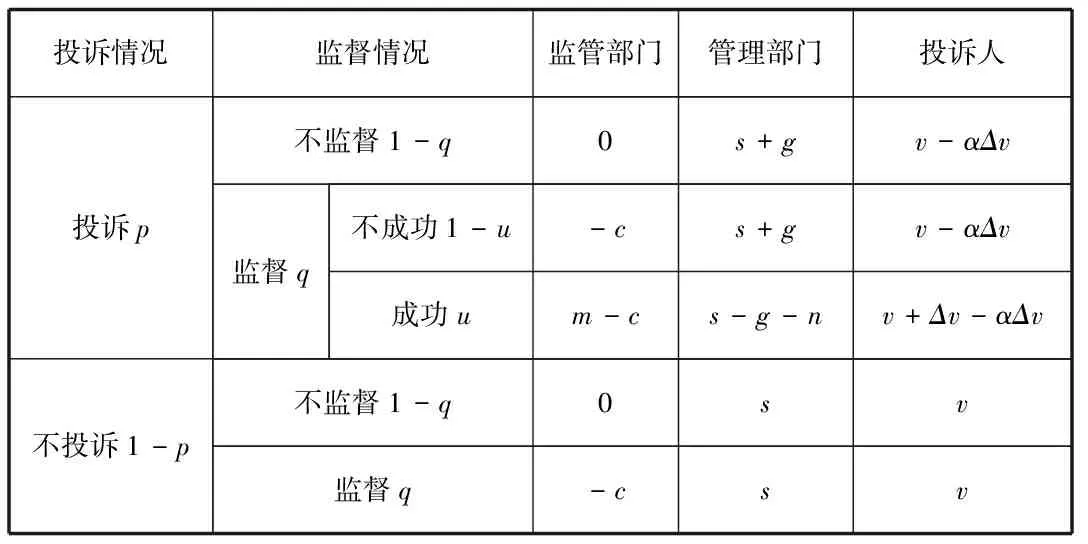
表1 博弈支付模型

(二)对模型进行求解

1.监督部门的期望总收益为E1：

E1=p(1-q)×0+pq(1-u)(-c)+pqu(m-c)+(1-p)(1-q)×0+(1-p)q(-c)

对q求一阶导数得：

∂E1/∂q=pum-c

令：∂E1/∂q=0

推导可得投诉概率p的最优值为：

p*=c/um

p>p*时，监管部门进行监管最为有利，p

2.管理部门接受投诉与不接受投诉的总收益为E2，则

E2=p(1-q)(s+g)+pq(1-u)(s+g)+pqu(s-g-n)+(1-p)(1-q)s+(1-p)qs

对p求一阶导数得：

∂E2/∂p=g-2qug-qun

令：∂E2/∂p=0

推导可得监督部门监督概率的最优值为：

q1*=g/u(2g+n)

当qq1*时，管理部门不接受投诉人投诉对其最有利，q=q1*时，管理部门接受投诉和不接受投诉的收益相等。

3.投诉人进行投诉与不进行投诉时的期望总收益为E3，则

E3=p(1-q)(v-αΔV)+pq(1-u)(v-αΔV)+pqu(v+ΔV-αΔV)+(1-p)(1-q)v+(1-p)qv

对p求一阶导数得：

∂E3/∂p=quΔV-αΔV

令：∂E3/∂p=0

推导可得监督人监督概率的最优值为：

q2*=α/u

当qq2*时，投诉人的最优选择为不投诉，

当q=q2*时，投诉人的投诉和不投诉的收益相等。

三、对博弈模型均衡解的讨论

综合上面的计算可得出高校评奖评优中的三方博弈模型的混合战略纳什均衡解为：

(p*，q1*)=[c/um，g/u(2g+n)]

(p*，q2*)=[c/um，α/u]

(一)对投诉概率最优解的讨论

由p*=c/um可知，投诉概率最优值p*与监督成本c、监督成功的概率u、监督部门的收益m有关。p*随着监督成本的增加而增加，即监督成本c越大，腐败行为发生的可能性就越大，投诉行为越有可能发生，因此要提高监督效率u，尽量降低监督成本，减少寻租行为的发生；p*随着监督成功概率u的增加而减少，即监督成功的概率越大，管理部门的腐败几率就越少，投诉行为就越不容易发生；p*随着监督部门的监督收益m的增大而减小，可理解为，监督部门的收益来自于对管理部门的处罚，当m越大说明管理部门的寻租风险越高，发生寻租的可能性就越低，发生的投诉就越少。

(二)管理部门利益最大化倾向的情况

如果把评优活动中管理部门的利益放在第一位，投诉者的利益放在第二位，则监督部门将以最优概率q1*=g/u(2g+n)进行监督。管理部门利益最大化情况下的纳什均衡解为(p*，q1*)，此时监督部门的最优监督概率为q1*，从上面的公式可知，q1*与管理部门的被投诉支付g、监督成功的概率u及监督部门对管理部门的惩罚n有关。如果管理部门的被投诉支付g=0，则q1*=0，即此项评优活动对管理部门没有收益，换句话说就是管理部门的评优活动是公平的，故没有管理偏失行为发生，无需监督，随着管理部门的被投诉支付g的增加，监管部门的监督概率q1*也相应增加；监管部门的最优监督概率q1*随监督成功的概率u的增加而减少，即监督成功的概率越大，管理部门的腐败几率就越少，最优监督概率q1*也就越小；监督部门发现投诉行为后对管理部门的惩罚n越大，就越能减少管理部门的寻租行为发生，即建立对管理部门的问责机制可以有效防止腐败的发生。

(三)投诉者利益最大化倾向的情况

如果把评奖评优活动中投诉者的利益放在第一位，管理部门的利益放在第二位，则监管部门将以最优概率q2*=α/u进行监督。投诉者利益最大化情况下的纳什均衡解为(p*，q2*)，此时监督部门的最优监督概率为q2*，从上面的公式可知，q2*与监督部门监督成功的概率u、投诉者的投诉成本系数α有关。α越大，投诉者的投诉成本越高，相应的管理部门的被投诉支付收益越高，腐败发生的可能性越大，监督部门的最优监督概率q2*也越大；如果α=0，则投诉者的投诉成本为0，投诉者的收益达到最大值V+ΔV，匿名投诉时即为此类博弈，投诉方的收益最大，监督概率q2*为0，即对于匿名投诉，管理方的最佳选择是不予受理；如果α=1，说明此时的投诉成本最大，投诉者通过投诉获得的最大收益为V，投诉为了公平，不为自己的收益，此时对于监督部门来说，最优监督概率也将增大；监督部门的最优监督概率q2*随监督成功的概率u的增加而减少。

四、对策建议

(一)增强投诉者的投诉成本并不能降低投诉行为的发生

根据上面对纳什均衡解的讨论可以很好的解释当前高校学生工作中的匿名投诉行为。目前高校中，评优中投诉问题层出不穷，多为匿名投诉，究其原因在于投诉者匿名投诉时几乎没有任何支付成本，投诉者心中的想法为，如果不投诉将不会有ΔV的收益，匿名投诉就有可能获得ΔV的收益，另外投诉者了解，监督部门不作为，将会有更上级管理部门问责，所以监督部门会处理所有投诉，作为监督部门对于这类投诉最好的处理办法就是建章立志，不予受理；增加投诉者的投诉成本并不能降低投诉率，对于监督部门来说，只有建立完善的问责机制才可以降低投诉机会，可以降低投诉率。

(二)适当增加管理部门的正常收益

管理部门的总收益值是恒定的，当增加管理部门的正常收益值时，管理部门的被投诉收益值就减少，g越小，可以减少管理部门的腐败和失责行为。这个正常收益可以是增加物质待遇也可以是提高管理人员的晋升机会，因为管理部门的正常收益越大，其腐败和失责行为被发现后损失就越大，即腐败风险越大，对失去既得收益的担忧在一定程度上可以降低管理部门的腐败行为，这时监督人就可以适当减小监督概率，这也与“高薪养廉”的道理一致。

(三)加大对监督部门的绩效考核

监督部门可以设置重金奖励提供腐败线索的证人及内部员工等措施，提高监督成功率，加大对管理部门寻租的惩罚，降低投诉率。

[1]孙萍，丁华.高校科技成果评价中的寻租博弈分析[J].湖南大学社会科学学报，2016(4)：106-109.

[2]洪必纲.我国寻租理论的研究现状与展望[J].统计与决策,2009(7):138-139.

[3]王欣，贾元华，马晓飞.国家科技计划项目立项中的寻租博弈分析[J].科技进步与对策，2011(8)：27-30.

[4]梁保磊，张玉林.寻政府科技项目寻租治理及最优监管度研究[J].科技管理研究，2009(6):56-58.

[5]赖经洪，程术兵.高校学生维权意识增强与学生管理对策研究[J].江西教育学院学报，2011(6):184-186.

HowtoSolvetheComplaintsintheAwardsofStudentsWorkUnderGameTheoryPerspective

Based on the analysis of the problem in the college students work,a complain game model is built up and solved.Then the paper gives the policy implications of the parameters and variables through the Nash equilibrium solution and provides the government approach to deal with complaints game.

game theory；college students work；complain；countermeasure

常笑(1993-)，女，马鞍山人，温州医科大学硕士研究生，研究方向：学生管理、护理管理等。