The influence of wave surge force on surf-riding/broaching vulnerability criteria check*
2017-09-15PeiyuanFeng封培元ShemingFan范佘明JunNie聂军XiaojianLiu刘小健
Pei-yuan Feng (封培元), She-ming Fan (范佘明), Jun Nie (聂军), Xiao-jian Liu (刘小健)
1.Marine Design & Research Institute of China, Shanghai 200011, China
2.Science and Technology on Water Jet Propulsion Laboratory, Shanghai 200011, China, E-mail: pyfeng23@163.com
3.Shanghai Key Laboratory of Ship Engineering, Shanghai 200011, China
The influence of wave surge force on surf-riding/broaching vulnerability criteria check*
Pei-yuan Feng (封培元)1,2, She-ming Fan (范佘明)1,3, Jun Nie (聂军)1, Xiao-jian Liu (刘小健)1,2
1.Marine Design & Research Institute of China, Shanghai 200011, China
2.Science and Technology on Water Jet Propulsion Laboratory, Shanghai 200011, China, E-mail: pyfeng23@163.com
3.Shanghai Key Laboratory of Ship Engineering, Shanghai 200011, China
This study focuses on the influence of the wave surge force on the assessments of the surf-riding/broaching vulnerability criteria according to the new proposal of the IMO Second Generation Intact Stability Criteria. A code is developed for the criteria check and the sample ship calculations show that the accuracy of the wave surge force estimation has a significant influence on the assessment result. For further investigation, the wave surge force measurement through a captive model test is made for a purse seiner to validate the numerical model, the effects of the wave steepness and the ship forward speed on the wave surge force responses are also discussed. It is demonstrated that the diffraction effect is important for the correct estimation of the wave surge force. Therefore, it is recommended to include this effect in the assessment procedure.
Intact stability criteria, surf-riding/broaching, sample calculation, wave surge force, captive model test
Introduction
In order to ensure the safety of ships in waves more effectively, the International Maritime Organization (IMO) is currently working on the second generation intact stability criteria to include five new stability failure modes: the pure loss of stability, the parametric roll, the dead ship condition, the surf-riding/broaching and the excessive acceleration[1,2]. Among them, broaching is considered to be the most complicated due to its highly nonlinear and chaotic nature[3,4]. The broaching occurs when a ship cannot keep a constant course despite the maximum steering effort, typically in the following and quartering waves.The surf-riding is usually regarded as the prerequisite of the broaching when a ship is captured by the wave approaching from the stern that accelerates the ship to the wave celerity[5]. Small-size high-speed ships are most vulnerable to this stability failure mode.
The mechanism behind this hazardous phenomenon, was extensively studied both theoretically and experimentally in recent decades. Maki et al.[6,7]and Wu et al.[8]made surf-riding predictions through theoretical formulations based on heteroclinic bifurcation. Umeda et al.[9-11]carried out free running model experiments and demonstrated that a ship complying with the existing IMO stability code can still be capsized as a result of broaching. Hashimoto and Stern[12]and Carrica et al.[13]applied the CFD method for an advanced broaching prediction to identify more details behind this phenomenon. Yu et al.[14]studied the influence of hull parameters on the mitigation of surf-riding. Another breakthrough is the proposal of the analytical formulae based on the Melnikov method and the split-time formulation for predicting the ship surf-riding threshold in the following seas[15,16], which forms the foundation for the development of surf-riding/broaching vulnerability criteria.
According to the latest IMO draft document[17], a three-level approach is adopted for the assessment of the surf-riding/broaching vulnerability criteria: in the Level 1 evaluation, only the ship length and speed information is required, the Level 2 evaluation is based on a simplified surf-riding model and the probability of the surf-riding occurrence in an irregular seaway is chosen as the criteria for assessment, the Level 3 evaluation involves a direct stability assessment and the detailed procedures are still under discussion[18].
This paper focuses on the influence of the wave surge force on the Level 2 assessment result. Studies concerning the parametric rolling show that the reliability of the wave force estimation plays an important role in the prediction model[19-21]. However, its influence on the assessment result of the surf-riding/broaching stability failure remains an issue to be explored. In the current prediction model, only the Froude-Krylov component of the wave surge force is taken into account. As pointed out in Ref.[17]: for calculating the amplitude of the wave surge force, the Froude-Krylov component on its own might often be over-estimated. Correspondingly, an empirical diffraction effect correction factor is proposed. On the other hand, the current wave force estimation model is based on the linear theory (with the small wave amplitude assumption) and the effect of the ship forward speed is neglected. However, a large wave heights and a high ship speed are necessary for the occurrence of surf-riding/broaching. Therefore, it is meaningful to measure the wave surge forces by the captive model experiment in order to validate this empirical formula and investigate the effect of the wave steepness and the ship forward speed.
1. Vulnerability criteria for surf-riding/broaching
The assessment procedures for the Level 1 and Level 2 surf-riding/broaching stability failure are based on the contents of Annex 32 and Annex 35 in SDC 2/INF.10[17], which is the latest draft document available. The criteria apply to all ships with length equal to, or greater than 24 m. Assessments should be performed for each loading condition of the ship.

For a ship to pass the assessment of the Level 2 vulnerability criteria, it is required that

whereCrepresents the probability of the surf-riding occurrence,RSRis the standard value, which is 5×10-3. The value ofCis estimated by
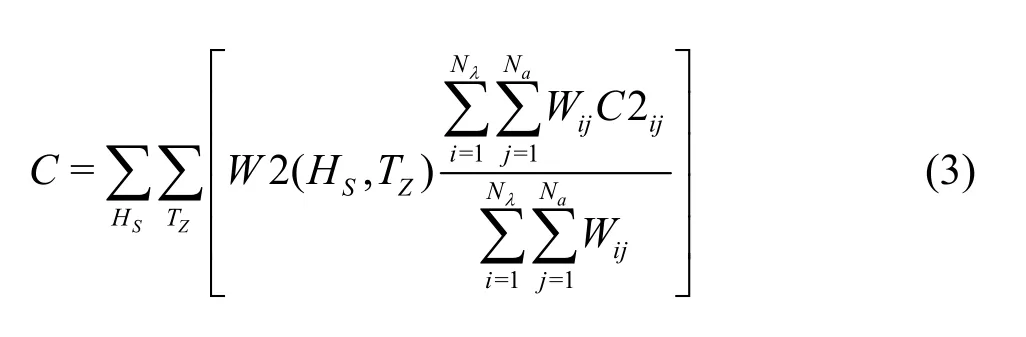
whereis the weighting factor of each sea state according to the long-term wave statistics,is the significant wave height,TZis the zerocrossing wave period,Wijis the statistical weight of a wave with the steepnessvarying from 0.03 to 0.15, and the ratio of the wave length to the ship lengthvarying from 1.0 to 3.0. Details concerning thecalculations of these factors are specified in SDC 2/INF.10[17].
is the key element indicating whether surfriding/broaching will occur for each wave case, which is defined as:


whereR(u) is the calm water resistance of the ship approximated by anNth order polynomial

is the propeller thrust in calm water, which is modeled by:
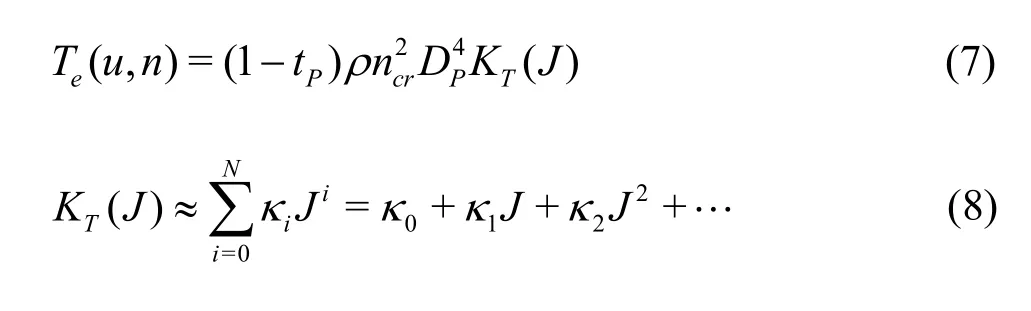

wheretPis the thrust deduction factor,wPis the wake fraction,DPis the propeller diameter.
The Melnikov method is adopted for solvingncr, based on a nonlinear surging equation

whereξGrepresents the longitudinal position of the ship center of gravity relative to the wave trough,mis the ship mass,mxis the added mass in the surge direction,fis the amplitude of the wave surge force, andkis the wave number.
The detailed application of the Melnikov method can be found in Ref.[15], and the following equations are included in the latest draft criteria to obtainncr:

wherecwis the wave celerity.
The amplitude of the wave surge force in Eq.(11) is calculated as:

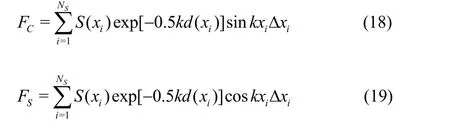
whered(xi) andS(xi) are the draft and the submerged area of the ship at the stationiin calm water, respectively.
Because Eq.(17) only cocnerns the Froude-Krylov component of the wave surge force, an empirical correction factorμxfor the diffraction effect compensation is proposed:
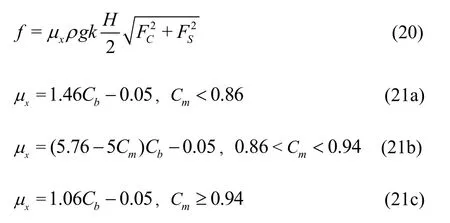
whereCbis the block coefficient,Cmis the midship section coefficient. It should be pointed out that the validity of this empirical correction has not been proved, which is still under discussion in IMO.
Based on the above method and procedures, a numerical code is developed for the assessment of the subsequent surf-riding/broaching vulnerability criteria.
2. Sample ship calculation
The main particulars of the sample ships are listed in Table 1. The length perpendicularLPPis taken as the ship lengthLin this study. The offset data, the calm water resistances and the propeller open water data of the sample ships are provided by the design institutes.
Fishing boats and small-size high-speed boats are chosen intentionally because they are most vulnerable to the broaching stability failure. Moreover, the Froude numbers of the sample ships are above 0.3 and none of the ship length is over 200 m. Therefore, none of the sample ships can pass the Level 1 evaluation.
For the Level 2 evaluation, the calm water resistance curves and the propeller thrust coefficients are approximated by the 5th and 2nd order polynomials, respectively. The assessment results are summarized in Table 1. TheCvalues are calculated either with or without the diffraction effect correction, denoted byCandC(μx). As can be seen from the results, the diffraction effect correction has a significant influence on the attainedCvalue. Once the diffraction effect is corrected, the attainedCvalue is decreased by about 40%-70%, which implies that the correct estimation of the wave surge force is crucial for the Level 2 assessment. Therefore, it is necessary to carry out further experimental investigations for a more accurate wave surge force prediction.
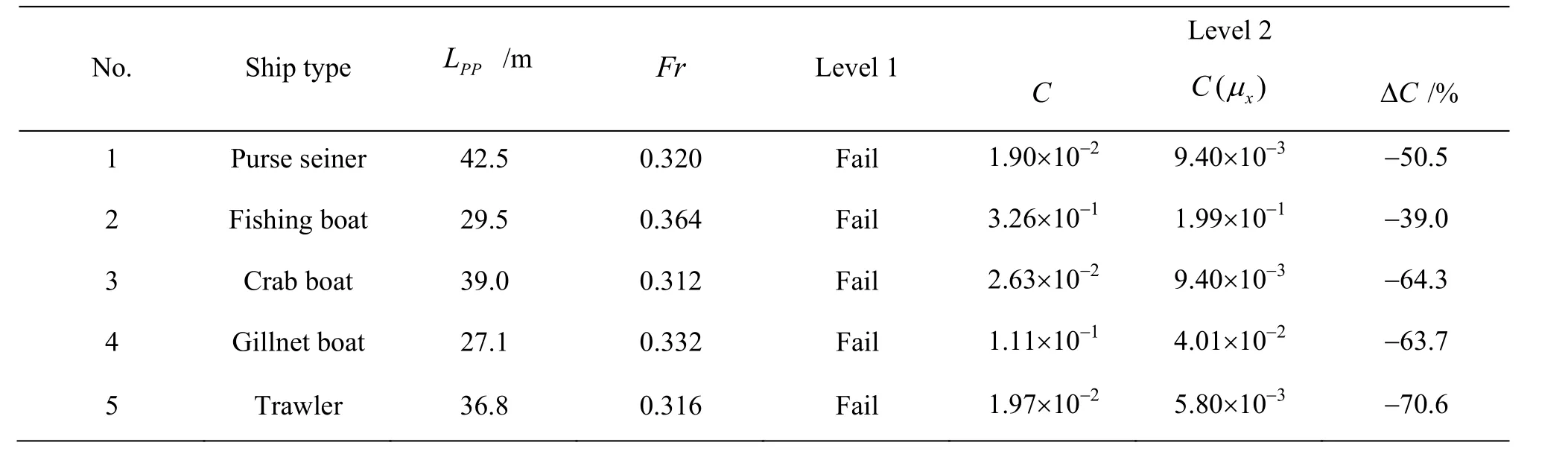
Table 1 Main particulars of sample ships and assessment results

Fig.1 Captive model test setup for wave surge force measurement
3. Captive model test
The captive model test in regular waves is performed to measure the wave surge force for a purse seiner (No. 1 ship in Table 1). This ship is a single propeller ocean-going vessel commonly found in China. The main particulars of the ship model (with a scale ratio of 17) are listed in Table 2.
The experiment is conducted in the towing tank of MARIC (Marine Design and Research Institute of China). The basin is 280 m long, 10 m wide and 5 m deep.
The experimental setup is illustrated in Fig.1. The ship is connected to the carriage. For the conventional seakeeping experiment, the ship is free to heave through one heaving pole. However, for the captive model test, an additional heaving pole is needed and two heave restrictors are applied to confine the heave and the pitch motions of the ship. Co-rrespondingly, two 3-component force sensors are installed between the heaving pole and the ship to measure the forces in the surge direction. The summation of the forces from the two sensors is taken as the measured wave surge force, i.e., the Froude-Krylov force plus the diffraction force. For tests with a forward speed, the ship is towed in calm water first to measure the reference forces of the two sensors, which is later deducted from the total measured wave surge force.
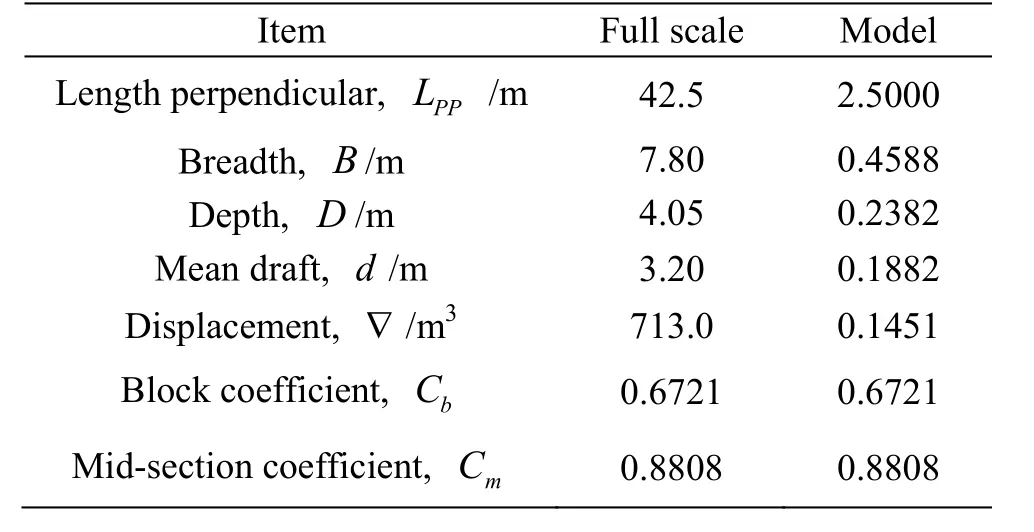
Table 2 Main particulars of the purse seiner
The experiment conditions are summarized in Table 3. Regular following waves are generated by the wave generator. Both cases of zero speed and ship speed ofFr=0.3 are tested. Two sets of wave steepness are tested for the zero speed case, i.e.,andThe wave lengths cover a range ofwhenH/λ=0.02. Under the condition ofH/λ=0.05 andFr=0.3,the tested wave lengths are reduced due to the wave height generation limitations and safety considerations.

Table 3 Experiment conditions
Figure 2 is an illustration of the experiment, which compares the wave patterns when the wave crest is passing the midship to demonstrate the effect of the wave steepness and the ship forward speed. In the case ofH/λ=0.05, there is a clear change of the wetted hull surface, which violates the linear theory assumption. On the other hand, due to the forward speed, the wave field becomes more complicated because the incoming regular wave interacts with the constant wave generated by the hull. A distinct bow wave can be noticed in Fig.2 whenFr=0.3.
4. Results and discussions
The experiment results are post-processed and compared with the numerical results in order to see the effect of the large wave steepness and the ship forward speed on the resulting wave surge force. Two methods for the numerical prediction are adopted: one is the strip method introduced in Section 2 according to SDC 2/INF.10, the other is a frequency domain Green Function based the 3-D panel method. Both methods are based on the linear theory with the small wave amplitude assumption, and the wave force is calculated only up to the mean wetted hull surface incalm water. Moreover, with the method based on the strip method, the Froude-Krylov force component of the wave surge force is only considered without taking into account the forward speed effect, while with the 3-D panel method, both the Froude-Krylov force and the diffraction force are considered, taking into account the speed effect. The results based on the 3-D panel method are computed by the commercial software HydroSTAR developed by Bureau Veritas (BV).

Fig.2 (Color online) Experiment snapshots
Figures 3, 4 show the section model and the panel model for the numerical computation.
Fig.3 Section model

Fig.4 (Color online) Panel model of the purse seiner
The experimental and numerical results are shown in Fig.5. The wave surge forceFxis presented in the form of non-dimensional Response Amplitude Operators (RAOs).The major findings are summarized as follows:
(1) The comparison of the experimental results betweenandH/λ=0.05 with zero forward speed shows that the linearity keeps well in terms of theFxresponses to the wave amplitude. Therefore, the wave steepness does not influence the wave surge force response very much and the numerical methods based on the linear theory assumptions can be applied in the assessments of the Level 2 surf-riding/broaching vulnerability criteria.
(2) The comparison of the experimental results betweenFr=0 andFr=0.3 shows that the ship speed effect tends to increaseFxRAOs whenbut tends to decreaseFxRAOs whenλ/LPP=2.0 and 2.5. The numerical results according to the 3-D panel method show the same tendency. However, theFxRAOs with or without the speed effect do not see a great difference. Therefore, for the simplicity of computation, it is acceptable to neglect the speed effect in the Level 2 assessment.
(3) The comparison between the 3-D panel method and the experimental results shows that they agree reasonably well with each other, especially in the small wave length region. However, the experiment results in the large wave length region are a little larger than the numerical results. Generally speaking, the 3-D panel method is applicable for the wave surge force prediction in the Level 2 assessment.
(4) The comparison of the numerical results obtained by the 3-D panel method and the strip method without diffraction correction shows that the wave surge forces obtained by the latter method are over-predicted throughout the whole wave length range. Therefore, the diffraction effect correction is necessary if the strip method is applied.
(5) The comparison of the numerical results obtained by the 3-D panel method and the strip method with diffraction correction shows that their differences are reduced, especially in the large wave length region. However, noticeable discrepancies still exist, which may influence the final assessment result. Therefore, the proposed empirical correction model can help improve the wave surge force estimation accuracy but further modification is still desirable. The advantage of using an empirical correction model instead of the direct 3-D panel method computation lies in the fact that the strip method adopts simpler section models and requires less computation effort, which is more preferable for the Level 2 assessment.
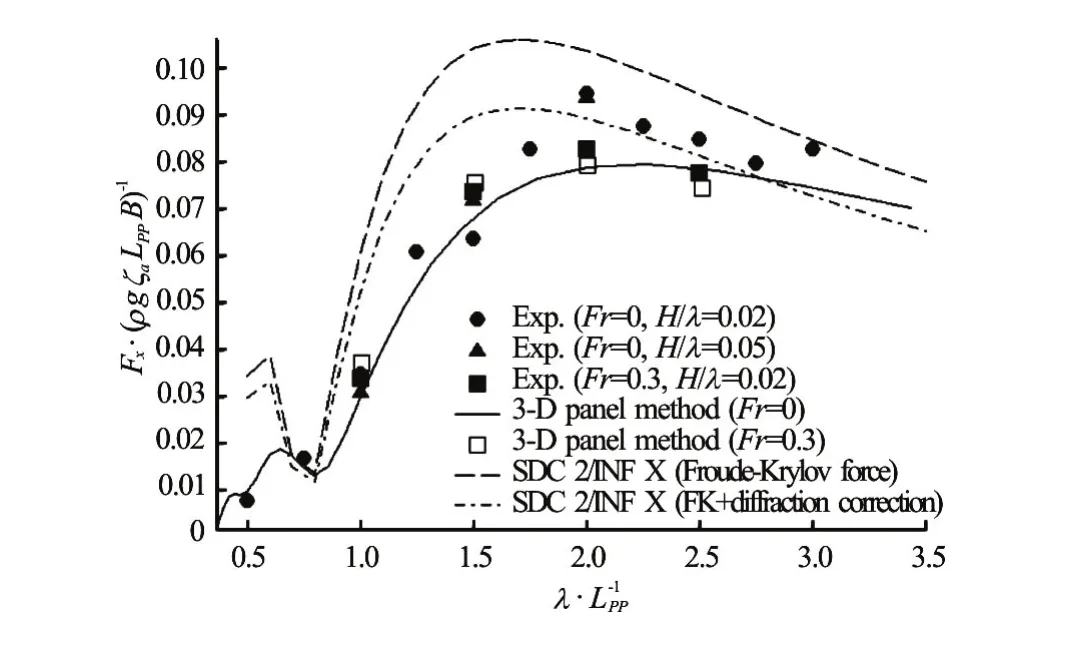
Fig.5 Comparison between experimental and numerical results
5. Conclusions
The influence of the wave surge force on the assessment of the surf-riding/broaching vulnerabilitycriteria according to the new proposal of IMO Second Generation Intact Stability Criteria is investigated. A code is developed for the check of the criteria. Sample ship calculations are performed, which show that the accuracy of the wave surge force estimation has a significant influence on the assessment result.
For a further investigation, the wave surge force measurement through a captive model test is made for a purse seiner in the towing tank. The influence of the wave steepness and the ship forward speed on the wave surge force is studied. It is demonstrated that:
(1) The wave steepness and the ship forward speed only have a secondary influence on the wave surge force responses. Therefore, it is acceptable to neglect the speed effect and adopt numerical methods based on the linear theory assumptions for the assessment of the Level 2 surf-riding/broaching vulnerability criteria.
(2) The diffraction effect is important for the correct estimation of the wave surge forces. Therefore, it is recommended to include this effect in the assessment procedure.
(3) The proposed empirical diffraction effect correction model can help improve the wave surge force estimation accuracy but further modification is still desirable.
This study demonstrates the validity of using the linear theory based methods for the estimation of the wave surge forces in the following regular waves despite the fact that the surf-riding/broach event is usually associated with a large wave amplitude and a high ship speed. The results can provide some guidance for IMO to finalize the new generation regulation. For future studies, more sample ship calculations are required for establishing a better empirical model for the diffraction effect correction.
[1] Umeda N. Current status of second generation intact stability criteria development and some recent efforts [C].The 13th International Ship Stability Workshop. Brest, France, 2013.
[2] Gu M., Lu J., Wang T. H. Stability of a tumblehome hull under the dead ship condition [J].Journal of Hydrodynamics, 2015, 27(3): 452-457.
[3] Themelis N., Spyrou K. J., Belenky V. “High runs” of a ship in multi-chromatic seas [J].Ocean Engineering, 2016, 120: 230-237.
[4] Neves M. Dynamic stability of ships in regular and irregular seas-An overview [J]. Ocean Engineering, 2016, 120: 362-370.
[5] Spyrou K. J., Belenky V., Themelis N. et al. Detection of surf-riding behavior of ships in irregular seas [J].Nonlinear Dynamics, 2014, 78(1): 649-667.
[6] Maki A, Umeda N., Hori M. Prediction of global bifurcation points as surf-riding points as surf-riding threshold in following seas [J].The Japan Society of Naval Architects and Ocean Engineers, 2007, 5: 205-215.
[7] Maki A., Miyauchi Y. Prediction methods for the surfriding threshold and the wave-blocking threshold based on Melnikov’s method [J].Journal of Marine Science and Technology, 2016, 21(2): 179-189.
[8] Wu W., Spyrou K. J., McCue L. S. Improved prediction of the threshold of surf-riding of a ship in steep following seas [J].Ocean Engineering, 2010, 37(13): 1103-1110.
[9] Umeda N., Matsuda A., Hamamoto M. et al. Stability assessment for intact ships in the light of model experiments [J].Journal of Marine Science and Technology, 1999, 4(2): 45-57.
[10] Umeda N., Hamamoto M. Capsize of ship models in following/quartering waves-physical experiments and nonlinear dynamics [J].Philosophical Transactions of the Royal Society A, 2000, 358: 1883-1904.
[11] Umeda N., Usada S., Mizumoto K. et al. Broaching probabilitiy for a ship in irregular stern-quartering waves: Theoretical prediction and experimental validation [J].Journal of Marine Science and Technology, 2016, 21(1): 23-37.
[12] Hashimoto M., Stern F. An application of CFD for advanced broaching prediction [J].The Japan Society of Naval Architects and Ocean Engineers, 2007, (5E): 51-52.
[13] Carrica P. M., Paik K. J., Hossein H. S. et al. URANS analysis of a broaching event in irregular quartering seas [J].Journal of Marine Science and Technology, 2008, 13(4): 395-407.
[14] Yu L., Ma N., Gu X. On the mitigation of surf-riding by adjusting center of buoyancy in design stage [J].International Journal of Naval Architecture and Ocean Engineering, 2017, 9(3): 292-304.
[15] Maki A., Umeda N., Renilson M. et al. Analytical formulae for predicting the surf-riding threshold for a ship in following seas [J].Journal of Marine Science and Technology, 2010, 15(3): 218-229.
[16] Belenky V., Weems K., Spyrou K. On probability of surfriding in irregular seas with a split-time formulation [J].Ocean Engineering, 2016, 120(1): 264-273.
[17] IMO. Proposed amendments to Part B of the 2008 IS code to assess the vulnerability of ships to the broaching stability failure mode [R]. SDC 2/INF.10, 2014.
[18] IMO. Draft guidelines of direct stability assessment procedures as a part of the second generation intact stability criteria [R]. SDC 1/INF.8, 2013.
[19] Matusiak J. E. On the non-linearities of ship’s restoring and the Froude-Krylov wave load part [J].International Journal of Naval Architects and Ocean Engineers, 2011, 3(1): 111-115.
[20] Hashimoto N., Umeda N., Matsuda A. Model experiment on heel-induced hydrodynamic forces in waves for broaching prediction [C].The 7th International Ship Stability Workshop. Shanghai, China, 2004, 144-155.
[21] Horel B., Guillerm P. E., Rousset J. M. et al. Experimental database for surf-riding and broaching-to quantification based on captive model tests in waves [C].The 14th International Ship Stability Workshop. Kuala Lumpur, Malaysia, 2014.
(Received March 6, 2015, Revised September 15, 2015)
* Project supported by the High-Technology Ship Research Project of Ministry of Industry and Information Technology (Grant No. K24352), the National Natural Science Foundation of China (973 Praogram, Grant No. 51579144).
Biography:Pei-yuan Feng (1987-), Male, Ph. D.,
Senior Engineer
She-ming Fan,
E-mail: fan_sm@maric.com.cn
猜你喜欢
杂志排行
水动力学研究与进展 B辑的其它文章
- ICHD’ 2018 The 13th International Conference on Hydrodynamics First Announcement
- Cavitation erosion in bloods*
- A GPU accelerated finite volume coastal ocean model*
- Mixing features in an electromagnetic rectangular micromixer for electrolyte solutions*
- A numerical study of violent sloshing problems with modified MPS method*
- Numerical investigation of entropy generation and heat transfer of pulsating flow in a horizontal channel with an open cavity*
