基于随机振荡序列离散灰色模型的优化

孔新海

（广安职业技术学院，四川 广安 638000）

基于随机振荡序列离散灰色模型的优化

孔新海

（广安职业技术学院，四川 广安 638000）

文章探讨了随机振荡序列灰色建模的问题，分析了两种具有代表性的基于振荡序列灰色建模方法，指出了其函数变换的实质以及应用范围。现有实证给出的建模方法其模型输出序列呈现出下凸的（除第一点外）和“Z字型”特点。结合这两种建模方法的优势，提出了另外两种数据变换方法，即加权均值平滑变换和级比调节平滑变换，实例说明了新的两种数据变换方法能有效地提高建模精度。

随机振荡序列；DGM(1，1)模型；平移变换；平滑变换

0 引言

灰色预测模型是灰色系统理论体系的重要内容，针对小样本数据通过累加生成就能有效揭示系统未来发展趋势[1]。由于灰色预测模型对数据没有严格的要求和限制，建模过程简单，受到越来越多学者重视，各种灰色模型不断被提出和优化，经过几十年的快速发展，已经被广泛应用于经济社会各领域，取得了非常好的应用效果[2]。但对随机振荡序列建立灰色模型进行预测时，学者们发现模型的模拟预测精度并不甚理想，原因在于灰色预测模型为指数形式，具有单调性，如果由该指数表达式计算出的模拟序列，其变化规律自然就不符合原始随机振荡序列的特征，导致模拟预测精度较差。为了拓广GM(1，1)模型的应用范围，文献[3]提出了通过加速平移变换将随机振荡序列转化为单调递增序列，再对单调递增序列进行累加均值生成，然后建立GM(1，1)模型。文献[4]则运用傅立叶级数修正GM(1，1)模型的残差，从而提高了振荡序列的模拟精度。文献[5]引入了平滑性算子来压缩随机振荡序列振幅以提高建模序列光滑度，并获得较高的模拟精度。文献[6]直接根据振荡序列的级比序列建立DGM(1，1)模型，进而用来预测原始序列。文献[7]通过对振荡序列的上下界序列分别建立非等间距GM(1，1)模型，得到上下包络曲线以描述系统发展的边界，采取区间预测算法。

通过文献中的例子佐证，上述函数变换在某些特定序列下具有较高的模拟精度，但还原精度并不理想。自身光滑性较差是随机振荡序列灰色建模精度不高的主要原因，而利用均值生成一些函数变换在一定程度上是可以提高建模序列的光滑度，但是加权均值生成并不能实质性改进随机振荡序列的光滑性且函数变换也无法从根本上改变随机振荡序列的振荡特征。本文利用平滑性算子可以压缩序列振幅特点，探索新的函数变换，以进一步提高灰色建模精度。

1 基本概念

定义 1[3]设X=(x(1)，x(2)，…，x(n))为一数据序列，

1）若∀k=2，3，…，n，有 x(k)-x(k-1)＞0，则称X为单调增长序列；

2）若∀k=2，3，…，n，有 x(k)-x(k-1)＜0，则称X为单调衰减序列；

3）若∃k，k′∈{2，3，…，n}有 x(k)-x(k-1)＞0 且 x(k′)-x(k′-1)＞0，则称X为随机振荡序列。设 M=max{x(k)｜k=1，2，…，n}，m＝min{x(k)｜k=1，2，…，n}，则称 T=M-m 为序列X的振幅。

定义2[3]设随机振荡序列为X=(x(1)，x(2)，…，x(n))，则称

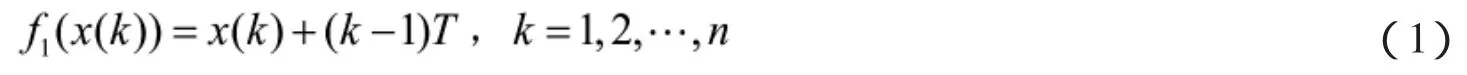
为加速平移变换；称

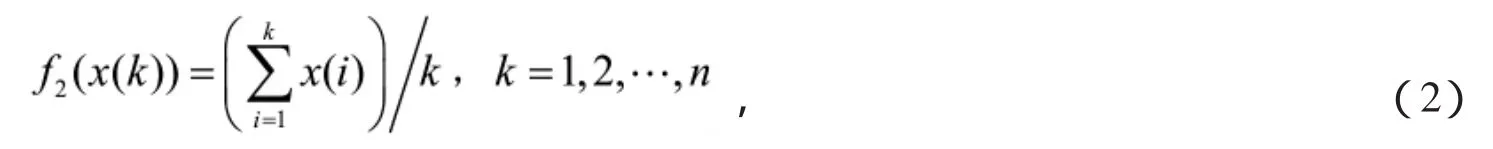
为加权均值生成变换。

定义3[5]设随机振荡序列为X=(x(1)，x(2)，…，x(n))，则称

为一阶平滑变换。

2 现有的两种建模方法比较

下面比较两种具有代表性的基于振荡序列灰色建模方法，所选验证数据分别来源于文献[3]和文献[5]，通过交叉验证来发现规律。

例1 我国 1978—1983 年的人均粮食产量为 X=(637，685，653，654，703，759)[3]，单位：斤。这是一组波动序列。文献[3]基于变换f1和f2建立GM(1，1)模型，而文献[5]是基于变换f3建立DGM(1，1)模型，其模拟结果见表1，拟合曲线如图1所示。

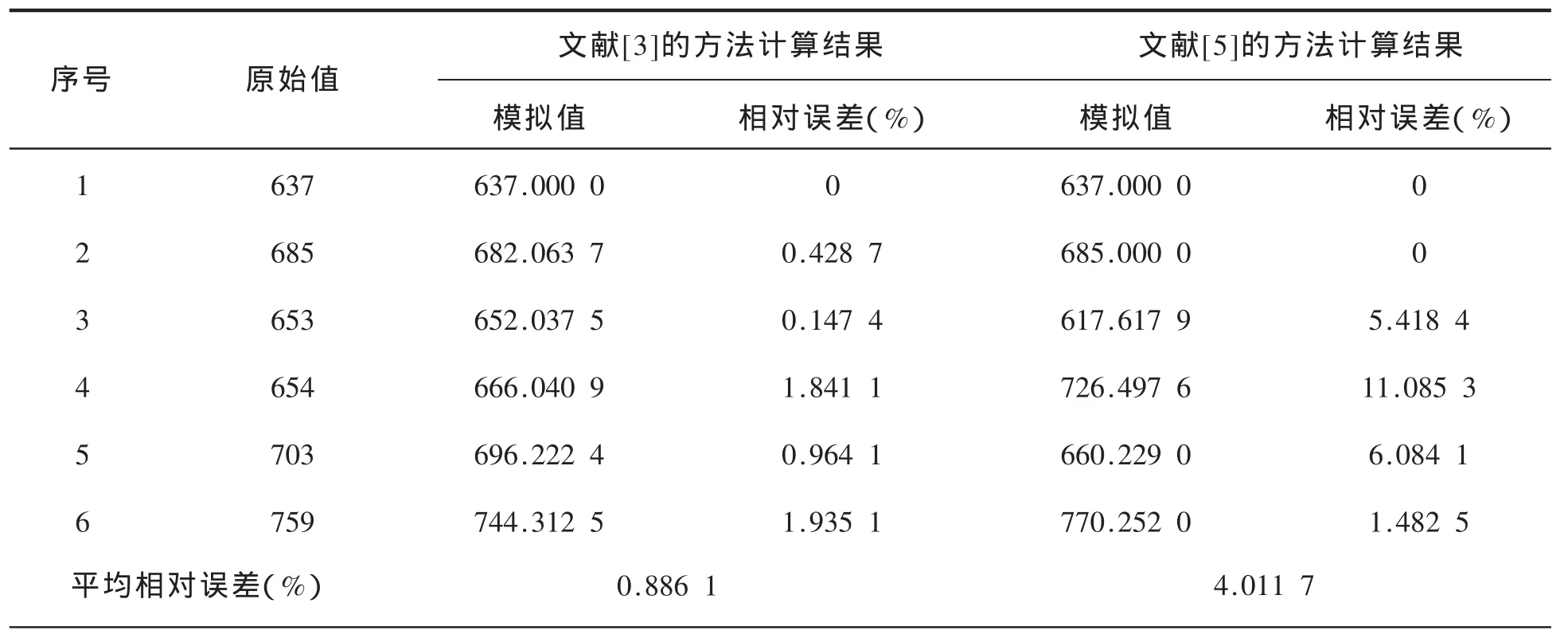
表1 两种建模方法结果对比

图1 两种建模方法对例1的拟合曲线

例2 一组振荡序列 X=(20.3，22.5，16.4，26.6，20.3，28.6)[5]，分别用文献[3]和文献[5]中的方法建立灰色预测模型，其模拟结果见表2，拟合曲线所图2所示。

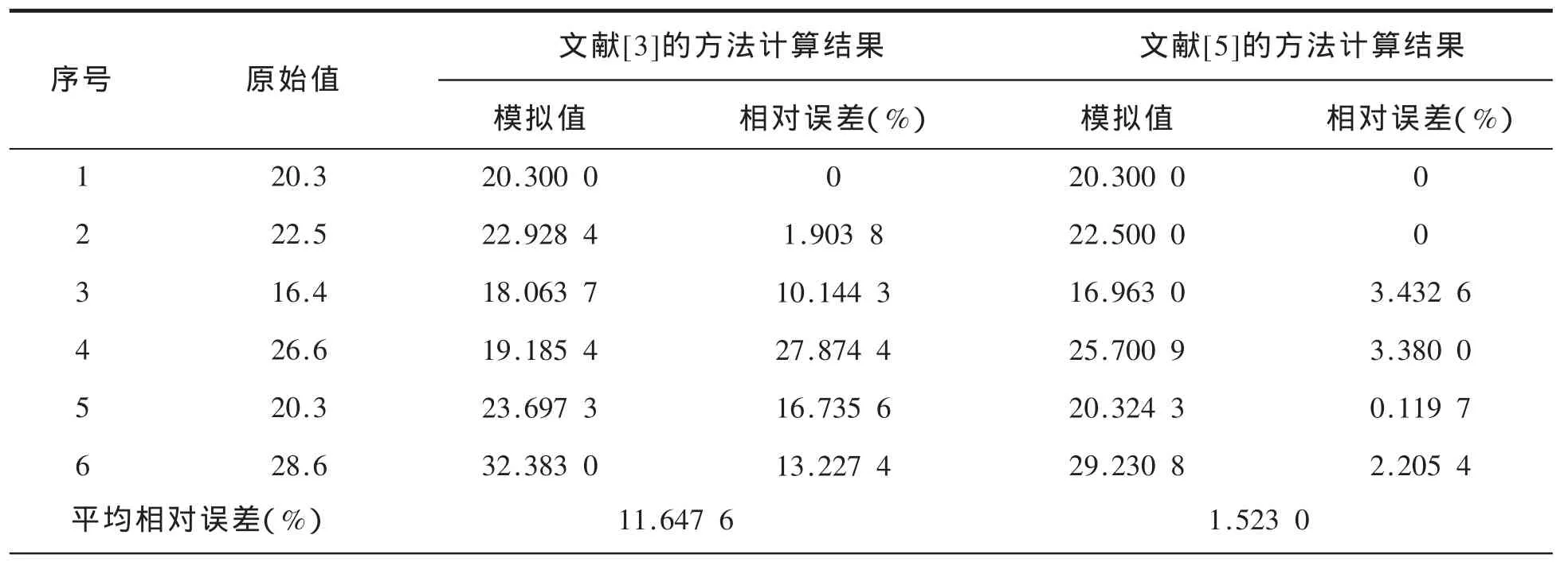
表2 两种建模方法结果对比

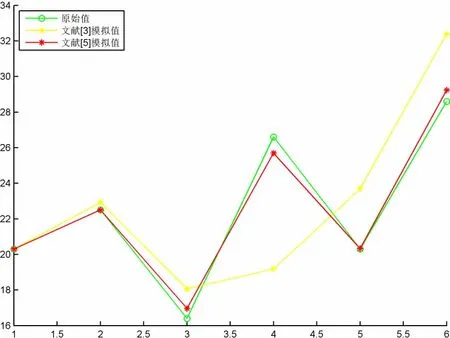
图2 两种建模方法对例2的拟合曲线

根据上面交叉验证，我们可以得到以下结论：

1）文献[3]建模方法得出的拟合曲线是下凸的（除了第一点外），所以不适合用于一般振荡序列的预测；

2）文献[5]建模方法得出的拟合曲线具有“Z字型”特点，这里把能够适用于“Z字型”特性的原始序列预测，称之为严格振荡数据序列预测；

3）对于毫无规律的振荡数据序列，建议采用区间包络法[7]或缩小级比偏差法[8]。

3 原因分析

文献[3]通过对原始振荡序列先进行加速平移变换，再进行加权均值生成变换，最后建立GM(1，1)模型，然后还原就得到模拟预测序列。这种建模的特点是把原始振荡序列转换成单调递增序列，再用累加均值化来弱化快速增长序列，其建模序列为

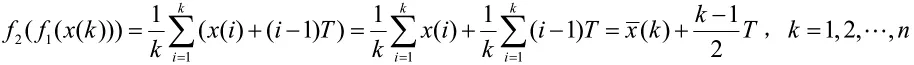
这就说明了原始振荡序列经两次变换之后成了累加均值序列与加速序列之和，看起来像是指数化了，但也提高了序列的增长率，级比偏差拉大，导致GM(1，1)建模误差过大，从而模拟序列成近似指数型（除第一点外）。

文献[5]运用一阶平滑变换对随机振荡序列进行均值弱化，然后建立DGM(1，1)模型，其建模序列为

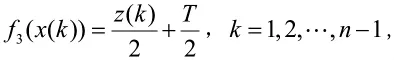
这里 z(k)=0.5(x(k)+x(k+1))，其中Z=(z(1)，z(2)，…，z(n-1))为原始序列的紧邻均值序列。由此可知，文献[5]针对严格振荡序列建模能够具有较高精度的本质不在于平移了T和振幅压缩了T/2，关键在于一阶平滑算式，即相邻数据之和弱化了随机性。

其实，平滑变换(3)式中的分母可以是任意正数，而DGM(1，1)模型[9]的模拟与预测效果保持不变。这是因为

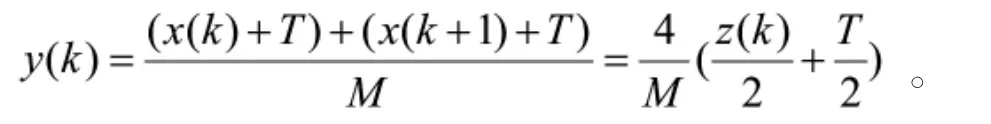
其中M是一个常数，且M＞0。文献[10]已证离散灰色模型经数乘变换不会改变模拟相对误差，虽然能缩小数据的量级，但不会改变模型的模拟与预测效果。

4 基于随机振荡序列DGM(1，1)建模的优化

由上面的分析，下面给出两种改进的变换算式：一种叫加权均值平滑变换；另一种叫级比调节平滑变换。

定义4 设随机振荡序列为X=(x(1)，x(2)，…，x(n))，则称

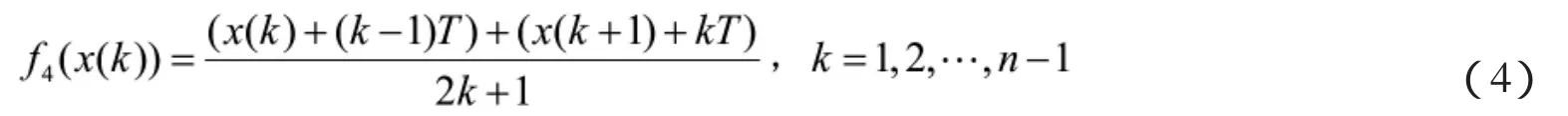
为加权均值平滑变换。

定义5 设随机振荡序列为X=(x(1)，x(2)，…，x(n))，则称

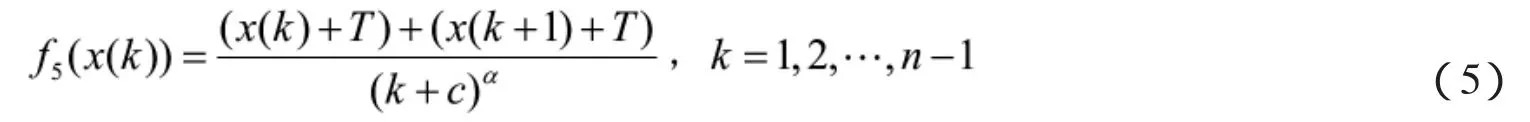
为级比调节平滑变换，这里要求k+c＞0，α∈R，c为平移参数，α为形状参数。对于参数c，α，可以采用二分法枚举，直到DGM(1，1)建模精度在允许范围之内。

由于直接对随机振荡序列建立的灰色预测模型精度较差而随机振荡序列的平滑序列具有较好的光滑性，因此，利用（4）式或（5）式对原始数据序列进行平滑变换处理，再构建变换序列的DGM(1，1)模型，最后进行逆变换。设数据序列 X(0)=(x(0)(1)，x(0)(2)，…，x(0)(n+1))，其变换序列为 Y(0)=(y(0)(1)，y(0)(2)，…，y(0)(n+1))。对序列 Y(0)建立 DGM(1，1)模型：

根据最小二乘法，可估计出[β1，β2]T=(BTB)-1BTY，其中

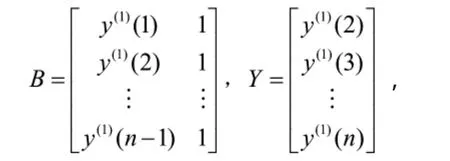
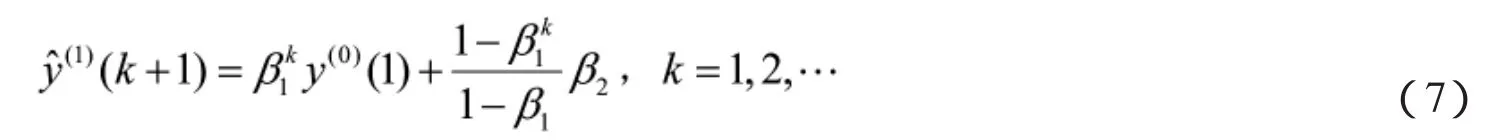
对(7)式进行累减还原，得到变换序列的模拟预测值

最后就(8)式进行逆变换，可得原始序列的模拟预测值

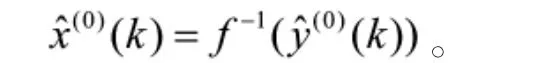
5 算例分析

下面还是以文献[5]中的序列 X=(20.3，22.5，16.4，26.6，20.3，28.6)为例，分别用上面加权均值平滑变换f4（本文方法一）和级比调节平滑变换f5（本文方法二）对原始数据进行预处理，再建立DGM(1，1)模型，其平均相对误差分别为0.9356%和0.8352%（见表3），要好于文献[3]和文献[5]得出11.6476%和1.5230%的拟合精度（见图3）。这里选择了c=T（原序列振幅），α=3。

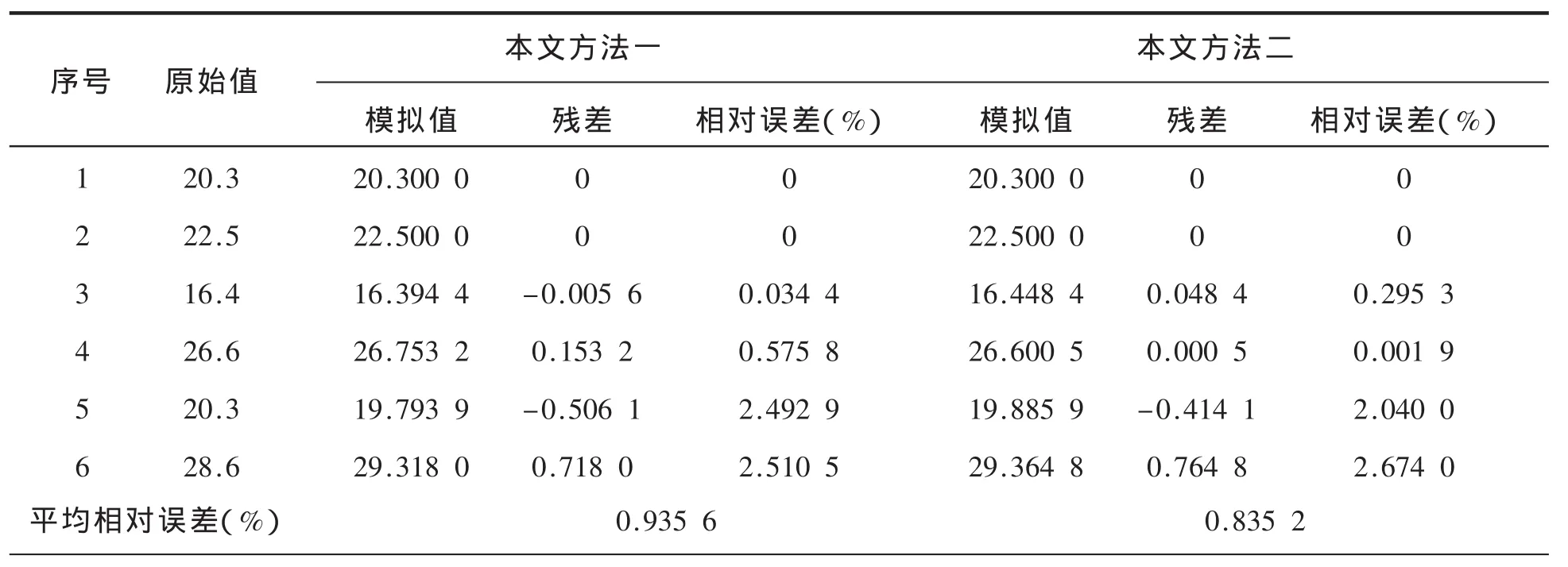
表3 两种建模方法模拟结果对比

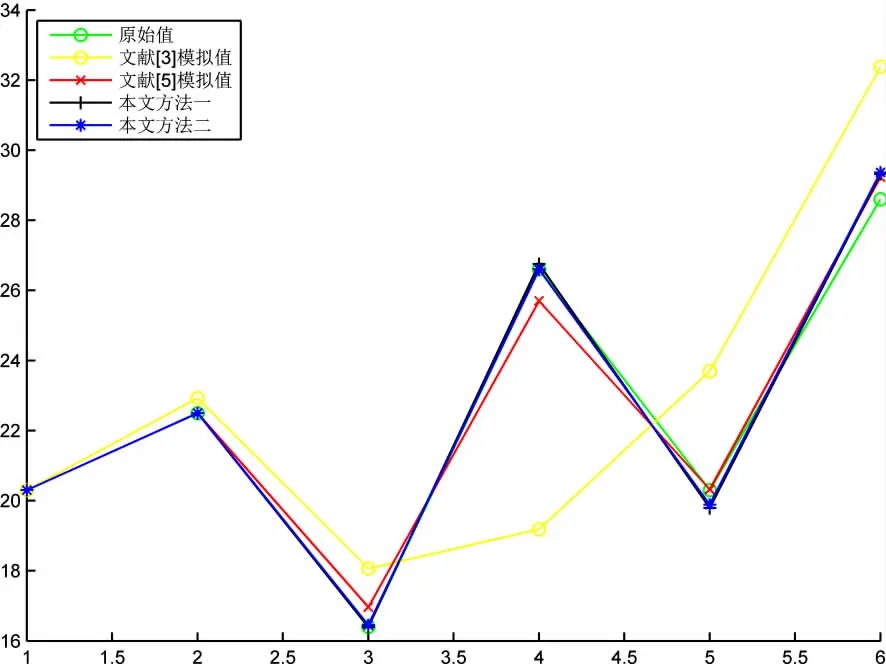
图3 四种建模方法的拟合曲线

6 结语

本文分析了两种基于振荡序列的灰色建模方法，指出了其中的函数变换仅仅适用于特定的数据序列，不具有广泛性。另外，振荡序列经变换之后能起到弱化随机性，光滑性条件得到提高，具有很高的模拟精度，但是还原序列的模拟精度会下降。文中也给出了两种函数变换，通过实例验证，这两种变换方法模拟精度有很大提高。最后需要说明的是，每种函数变换具有自身特点，要根据随机振荡序列的发展趋势合理选择数据变换方法再建灰色预测模型。

[1]DENG J L.Introduction to grey system theory[J].The Journal of Grey System，1989，1（1）：1-24.

[2]刘思峰，杨英杰.灰色系统研究进展[J].南京航空航天大学学报，2015，47（1）：1-18.

[3]钱吴永，党耀国.基于振荡序列的 GM（1，1）模型[J].系统工程理论与实践，2009，29（3）：149-154.

[4]王正新，党耀国，裴玲玲.基于 GM（1，1）幂模型的振荡序列建模方法[J].系统工程与电子技术，2011，33（11）：2440-2444.

[5]曾波，刘思峰.基于振幅压缩的随机振荡序列预测模型[J].系统工程理论与实践，2012，32（11）：2493-2497.

[6]杨保华，方志耕，张可.基于级比序列的离散 GM（1，1）模型[J].系统工程与电子技术，2012，34（8）：715-718.

[7]罗党，未保磊，李海涛，等.灰色区间预测模型及其性质[J].控制与决策，2016，31（12）：2293-2298.

[8]孙倩倩，魏勇.函数变换缩小数据级比偏差效果的比较原则[J].数学的实践与认识，2014（8）：254-259.

[9]谢乃明，刘思峰.离散 GM（1，1）模型与灰色预测模型建模机理[J].系统工程理论与实践，2005，25（1）：93-99.

[10]谢乃明，刘思峰.离散灰色模型的仿射特性研究[J].控制与决策，2008，23（2）：200-203.

Optimization of Discrete Grey Model Based on Stochastic Oscillation Sequences

KONG Xinhɑi
（Guang’an Vocational&Technical College，Guang’an Sichuan 638000，China）

This paper discussed the grey modeling problem of stochastic oscillation sequences and analyzed two kinds of representative grey modeling methods based on the oscillation sequences.Besides，the essence and the application scope of two function transformations were pointed out.The empirical results shows that the existing modeling methods are presented in which the model output sequence exhibits lower convexity（except for the first point）and the“Z”feature.By combining with the advantages of these two modeling methods，two other data transformation methods are proposed：the weighted average smooth transformation and the class ratio-adjusted smooth transformation.In conclusion，the example also shows that the two new data transform methods can effectively improve the modeling accuracy.

Stochastic Oscillation Sequence；DGM （1，1）Model；Translation Transformation；Smooth Transformation

N941.5

A

1009-8666(2017)08-0031-07

［责任编辑、校对：方忠］

10.16069/j.cnki.51-1610/g4.2017.08.007

2017-04-13

四川省教育厅科研项目“难采储量评价方法及其应用研究”（14ZB0388）

孔新海（1983—），男，江西余干人。广安职业技术学院讲师，博士，研究方向：不确定性预测与决策。