长波单项传播模型BBM方程精确解的研究

范慧玲

（黑龙江八一农垦大学理学院，大庆 163319）

长波单项传播模型BBM方程精确解的研究

范慧玲

（黑龙江八一农垦大学理学院，大庆 163319）

广义的BBM方程在物理上被用来研究长波单项传播情形。通过研究广义的BBM方程中的参数p取不同值时，根据方程的具体特点来寻找恰当的试探子方程，当p=1时，根据试探方程法得到子方程是一个二次多项式，应用二阶多项式完全判别系统法求得了它的精确解；当p=2时，我们得到的子方程是一个四次多项式，应用四阶多项式完全判别系统法求得了它的精确解并进行了分类；当p=4时，此时的子方程是一个三次多项式，应用三阶多项式完全判别系统法求得了它的精确解；用试探方程法对于不能化为初等积分形式的方程来求它的可能的精确行波解还是很有效的。

精确行波解；试探方程法；BBM方程；完全判别式法

非线性偏微分方程经常出现在数学物理和工程领域中，它们的精确解的求得是非线性科学领域的核心问题之一。多年来国内外数学物理学家都在研究求解偏微分方程精确解的方法[1-9]。精确解的求得也是实际数学物理力学模型方程的需要，实际问题如果能够求得精确解，尤其求出全部的精确解，有着重大的理论价值和实践意义。由于非线性微分方程的复杂性，求解的方法也灵活多变。试探方程法是当非线性偏微分方程经过行波变换为常微分方程后，仍不能化为初等积分形式时，根据方程的特点，应用试探方程法来寻找恰当的可积子方程，从而求得其可能的精确解。

广义的BBM方程是不同物理系统中出现的弱非线性色散介子中长波单项传播的重要模型方程。很多科研工作者们应用了一些方法求得了BBM方程的若干精确解，例如在文献[10]中应用齐次平衡原理得到了广义的Burgers-BBM方程的一些孤波解和周期解[10]；在文献[11]中应用Tanh函数法求得了BBM方程的一些精确解和周期解[11]。先研究学习试探方程法的理论，然后根据BBM方程的特点，给出适当的子方程来求解广义的Burgers-BBM的所有可能的精确解的分类。

1 试探方程法概述

设非线性偏微分方程为

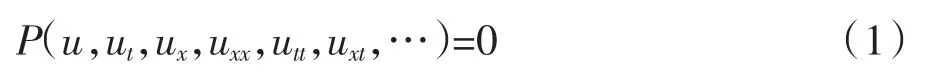
其中P是关于u，ut，ux，uxx，utt，uxt，…的多项式。

通过如下的行波变换，

方程（1）被约化成如下的常微分方程，

根据方程（3）的特点我们可以取试探子方程为

其中ai为常系数，

其中ai为常系数。

由方程（4）可导出

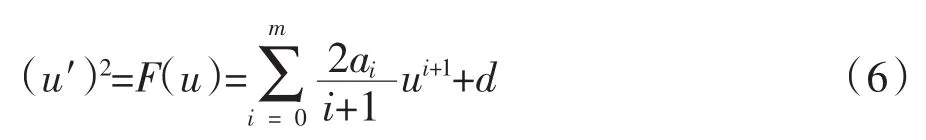
这里d是积分常数。

通过平衡分析可以确定（5）式和（6）式中m的取值。

对（6）式左右两端同时积分，可以得到以下形式

对（5）式进行同样的计算，可以得到

根据（7）和（8）中F（u）的阶数，根据相应的多项式完全判别系统法求出（7）和（8）的全部行波解的分类。

2 广义的Burgers-BBM方程精确解

广义的Burgers-BBM方程如下

当参数p取不同数值时，我们根据此时方程的特点，找出恰当的子方程，从而得到方程（9）的精确行波解。

行波变换u=u（ξ），ξ=x-ct，方程（9）可化为

2.1 p=1时的情形

当参数p=1时，方程（12）变为

令w=φ′，方程（15）变为

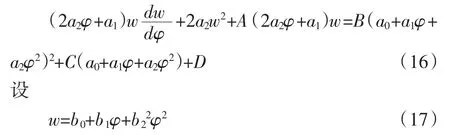
把（17）带入到（16）中，我们得到

2.2 p=2的情形

p=2时，方程（12）变为

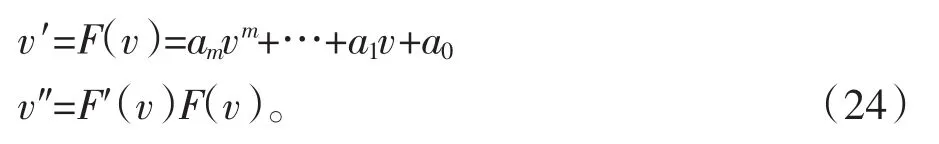
把（24）代入到（23）式中，通过讨论得到m=2。

从而得到下列两个等式：

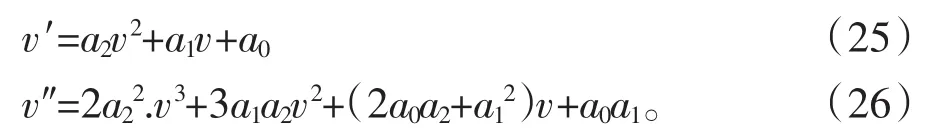
把（25）和（26）代入到（23）中，再根据平衡原理我们得到以下方程组

利用四阶完全判别系统，可以得到（30）的所有精确解及分类。

2.2.1 D4=0，D3=0，D2＜0。F（w）有一对二重共轭复根，设F（w）=［（w-l）2+s2］2，其中l，s是实数，s＞0。（30）的精确解为

2.2.2 D4=0，D3=0，D2=0。F（w）有四重零实根，设F（w）=w4。（30）的精确解为

2.2.3 D4=0，D3=0，D2＞0，E2=0。F（w）有两个不同的二重实根，设

F（w）=（w-α）2（w-β）2，α，β是实数，α＞β。当w＞α或w＜β，（30）的精确解为

当β＜w＜α，（30）的精确解为

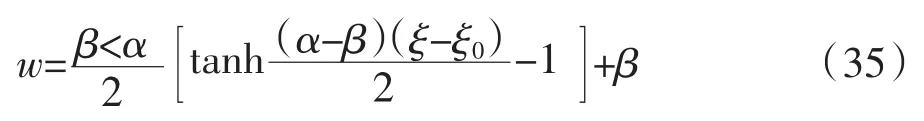
2.2.4 D4=0，D3＞0，D2＞0。设F（w）=（w-α）2（w-β）（wγ），其中α，β，γ为实数，β＞γ。

当α＞β，w＞β，或α＜γ，w＜γ，（30）的精确解为

2.2.5 D4=0，D3=0，D2＞0，E2=0。设F（w）=（w-α）3（wβ），其中α，β都是实数。当w＞α，w＞β，或w＜α，w＜β，（30）的精确解为

2.2.6 D4=0，D2D3＜0，设F（w）=（w-α）2［（w-l）2+s2］，这里α，l和s是实数。（30）的精确解为

2.2.7 D4＞0，D3＞0，D2＞0。F（w）=0有四个实根，设

F（w）=（w-α1）（w-α2）（w-α3）（w-α4），其中α1，α2，α3，α4是实数，并且α1＞α2＞α3＞α4。作变换

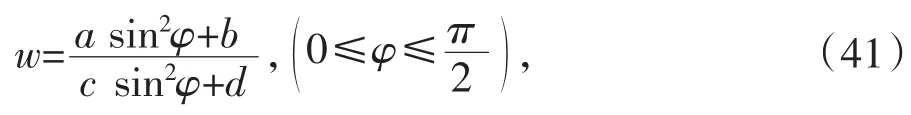
当w＞α1或者w＜α4时取

当α2＞w＞α3时取

由方程可得

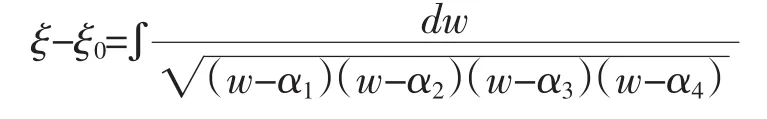
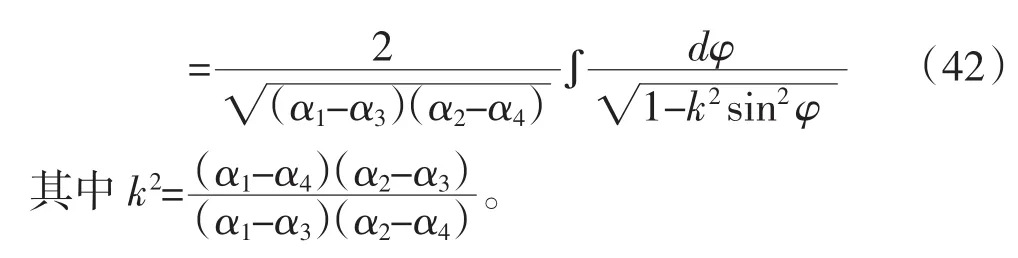
根据雅可比椭圆正弦函数定义，我们可得上述方程的解为

2.2.8 D4＜0，D2D3≥0。F（w）=0有两个不同的实根和一对共轭复根，设

其中α1，α2，l1和s1都是实数，且α1＞α2，s1＞0，假设

根据雅可比椭圆余弦函数的定义，我们可得方程的解为

2.2.9 D4＞0，D2D3≤0。F（w）=0有两对共轭复根，设

其中l1，l2，s1和s1是实数，且s1＞s2＞0。假设

根据雅可比正弦和余弦函数的定义，我们得到方程（30）的解为

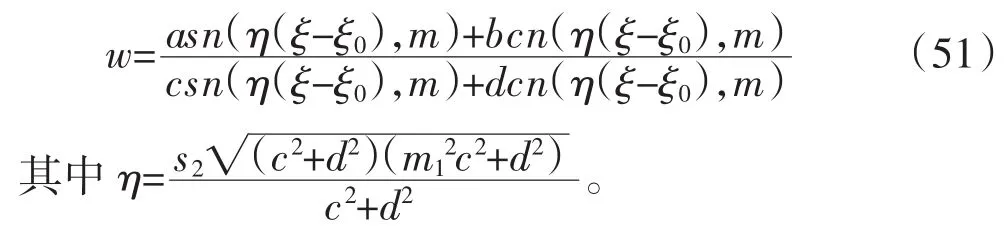
2.3 p=4的情形

p=4时，方程（12）变为

由（39）和（40）我们得到以下方程组

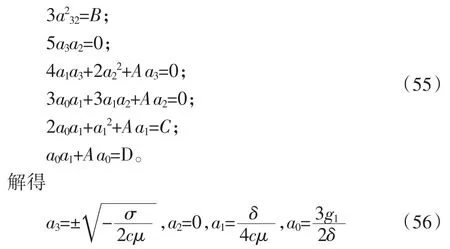
把（56）带入到（53）中并积分，我们有

我们得到积分式（52）相应的解为

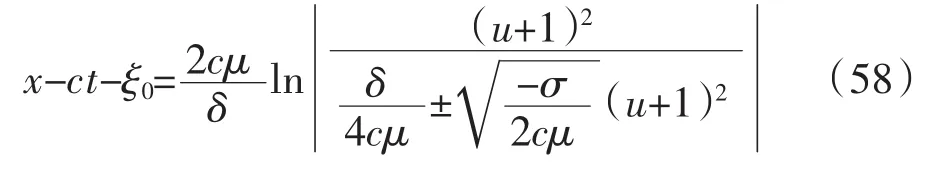
3 结论

根据BBM方程在参数p=1、p=2和p=4时的特点，应用试探方程法我们找到了适合方程的子方程，根据自方程的阶数我们应用多项式完全判别系统法求得了原方程在参数p=1、p=2和p=4时的所有可能精确行波解的分类，这里面包含了一些之前没有得到的新解。我们通过BBM方程来推广寻找子方程的方法，可以进行拓展应用到类似的方程上来求解更多偏微分方程的精确解。所求得的广义的BBM方程所有的精确解，可以更好的进行物理系统的研究。

［1］李欣，马文静.对称多右端项位移方程组的种子投影方法的研究［J］.黑龙江八一农垦大学学报，2015，27（6）：95-98.

［2］Cheng-shi Liu.Canonical-like transformation method and exact solutions to a class of diffusion equations［J］.Chaos，Solitons and Fractals，2009，42：441-446.

［3］Cheng-shi Liu.New trial equation methods and exact solution to some nonlinear mathematical physical equations［J］.Far East Journal of Applied Mathematics，2010，40（1）：49-64.

［4］Cheng-shi Liu.Trial equation method to noinlinear evolution equations with rank inhomogeneous［J］.mathematical discussions and its applications，Commun.Theor.Phys.，2006，45：219-223.

［5］曹剑英，刘凌云.CORDIC算法原理［J］.赤峰学院学报：自然科学版，2014（4上）：21-23.

［6］Liu C S.The representation and classification of all single traveling wave solutions to sinh-Gordon equation［J］.Commun.Theor.Phys.，2008，49（1）：153-158.

［7］Fan H L.The classification of the single traveling wave solutions to the generalized Equal Width equation［J］.Applied mathematicas and computation，2012，219：748-754.

［8］FAN HUI L，LI XIN.The classification of the single travelling wave solutions to the generalized Pochhammer-Chree equation［J］.Pramana，2013，81（6）：925-941.

［9］Fan Hui Ling，Fan Xue Fei，Li Xin.On the exact solutions to the long-short-wave interaction system［J］.Chin.Phys. B，2014，23（2）：020201.

［10］AM Wazwaz.The tanh-coth and the sine-cosine methods for kinks，solitons，and periodic solutions for the Pochhammer-Chree equations［J］.Applied Mathematics and Computation，2008，195（1）：24-33.

［11］鲍春梅.有关近于凸解析函数族的Hadamard卷积与Fekete-Szeg觟问题［J］.赤峰学院学报：自然科学版，2013（6下）：9-10.

Research on Exact Solutions to Long-wave Single Spread Model Equation

Fan Huiling
（College of Science，Heilongjiang Bayi Agriculture University，Daqing 163319）

The regularized Burgers-BBM equation was researched on the long-wave single spread.Applying the trial equation method to discuss the regularized Burgers-BBM equation，when the parameter p took 1，2 and 4，it obtained the corresponding subequation，then it gave the classification of the exact traveling wave solutions to the corresponding sub-equation by the complete discrimination system for polynomial method.The trial equation method was very effective to the equations which could not reduce elementary integral form.

exact traveling wave solution；the trial equation method；BBM equation；the complete discrimination system for polynomial method

O0175.29

A

1002-2090（2017）04-0128-05

10.3969/j.issn.1002-2090.2017.04.029

2016-10-09

黑龙江省教育厅科研项目（12531475）；黑龙江八一农垦大学校培育课题（XZR2016-13）。

范慧玲（1982-），女，东北石油大学毕业，现主要从事数学教育方面的研究工作。