主成分分析法在奎河水污染分析中的应用
2017-09-15宋紫阳
王 婷 宋紫阳 边 疆
主成分分析法在奎河水污染分析中的应用
王 婷 宋紫阳 边 疆
奎河发源于江苏省徐州市西南郊的云龙湖,为徐州市内重要的景观河道。随着城市化进程不断加快,日趋频繁和剧烈的人类活动使得奎河水质污染严重。最近十几年,奎河的开发与治理矛盾尖锐。因此,如何客观而准确地找出影响奎河水质的主要因素,对于奎河规划治理具有重要的意义。目前国内外常用于水环境评价方法有指数法、主成分分析法、模糊综合评价法、灰色数学法、神经网络法等,其中主成分分析法理论是比较完善的多元统计分析方法,在解决很多类似问题时已取得较好的效果。本文选择使用主成分分析方法进行实证分析,找出影响奎河水质的主要因素,定量化研究奎河水环境污染问题。
一、分析方法
1.基本思想
主成分分析(PrincipalComponents Analysis,PCA)是研究多个定量(数值)变量间相关性的一种多元统计方法。它是通过研究如何通过少数几个主分量(即原始变量的线性组合)来解释多变量的方差—共变量结构。具体地说,就是通过相关性分析,分离出少数几个主分量,保证它们能代表尽可能多的原始数据信息。主成分常被用来寻找判断某种事物或现象的综合性指标,并将综合指标所蕴藏的信息适当地解释,以便更深刻地表现事物内在的规律。
2.分析模型
(1)汇总分析指标,设需要分析的河流共有n个监测断面,k项监测指标,收集各断面某个时段(年、季、月)平均监测数据来构成原始数据矩阵为:

式中:X为各断面监测原始数据矩阵;xij是第i个断面的第j项监测数据。
为排除量纲和数量级的不同,对原始数据进行标准化处理,计算公式为:

同时,设X'为标准化矩阵,见下式:

(2)求解矩阵X'的相关系数矩阵R,并代入特征方程求解非负特征值λ(λ1>λ2>…λp>0)及对应的特征向量C1,C2,…Cp,其中Cm=(cm1,cm2,…,cmk)T且(m=1,2,…,p),并计算各分量的方差贡献率为:

式中:at为当前r个主分量的累计方差贡献率,若满足时,则前r个主分量对应的监测指标值为主成分。
(3)计算前r个主分量的主成分得分Yt,则:

(4)以各主分量方差贡献率为权数,构造分析函数,即:

式(4)中Fi代表第i个测站点水质指标的综合得分,综合得分越高,表明该段河流水环境质量污染越严重。出现负值说明综合水质情况达标,正值则超标。
(5)分析河流的污染源情况,即综合得分高的河段污染物超标,其中累计方差贡献率大于85%的指标为其主要污染物。
3.资料选取
本文选取徐州市水环境监测中心2013年奎河上五个水质监测段的平均监测数据,共11项监测指标作为分析资料,见表1。
二、结果与分析
1.数据标准化处理
对表1中数据进行标准化处理,结果见表2。

表1 奎河2013年水质监测均值表(单位:mg/L)
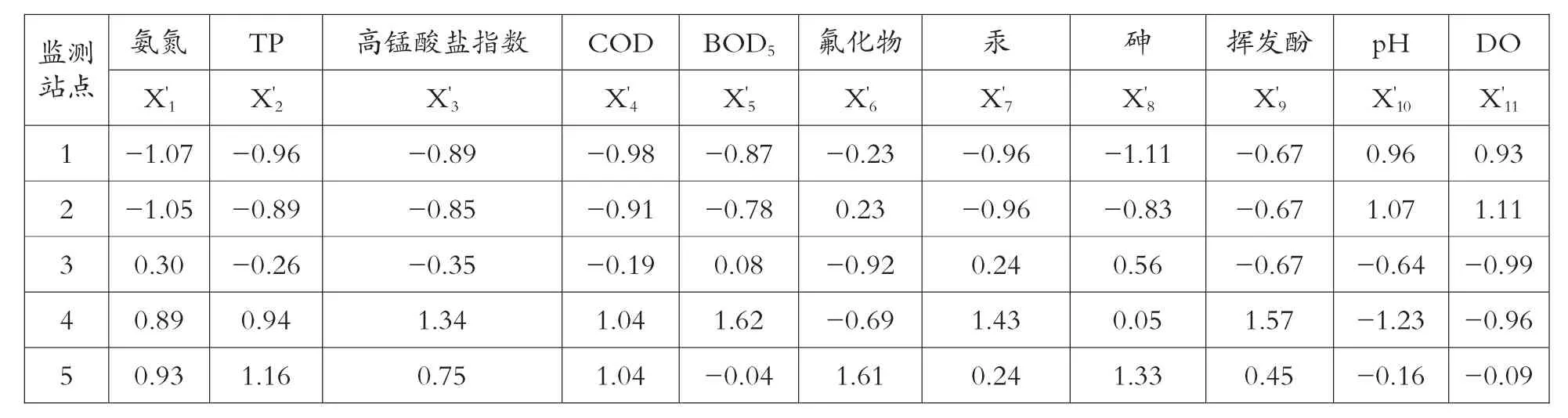
表2 标准化数据表

表3 特征值计算结果表
2.相关系数及特征根求解
将表2数据导入SPSS软件进行计算,很容易就得到了相关系数矩阵的特征值和特征向量,并计算各特征值对应主成分的方差贡献率,如表3所示。
由表3中的结果可知,前两个特征值对应主成分的累计方差贡献率已经达到92.45%>85%,故它们所对应的两个主成分已经能够反映原始指标的绝大部分信息,可利用它们对奎河五个检测段的水环境质量进行分析。按各主成分线性表达式中主成分特征值及对应的标准化数据,构造出两个主成分Y1和Y2函数如下:
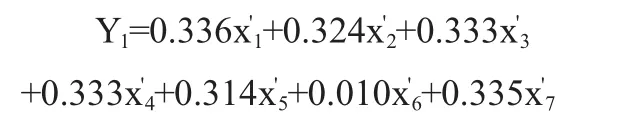
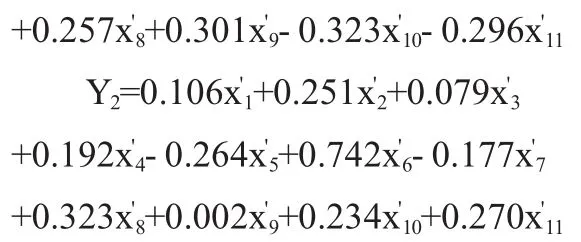
3.水污染综合分析
各主成分得分与对应的方差贡献率乘积的总和即为综合得分。最后计算出五个监测段各自的主成分得分及综合得分,得分越大,表明污染程度越严重,由此可对各断面的水环境质量状况进行排序和分级,最终结果见表4。
4.结果分析
(1)由表4的结果可知,奎河水污染情况不均衡,五个监测段中1、2号测段得分最低,污染程度最小;3号测段得分处于平均水平;4、5号测段综合得分最高,说明其污染程度最高。

表4 奎河水污染分析结果表
(2)由表2数据可知,在主成分中,氨氮贡献率为76%,总磷贡献率达到16%,绝对值较大,对奎河水质起主导作用;其次高锰酸盐、COD的贡献率为7.55%,也对奎河水质产生一定的影响。由于氨氮、总磷指数代表水体富营养化的营养元素的污染状况,因此,对于奎河的治理工作,应重点控制4、5号监测段的氨氮、总磷类污染源。
(3)本文的分析结果与2013年徐州市环境质量报告中的结果基本一致,说明此分析方法符合奎河的实际情况。
三、结束语
通过本文的实证应用,在多指标综合分析方面主成分分析法的优势明显,主成分分析法能够最大限度地减少水质监测数据信息损失量,以主要的变量来代替原有的多维数组,大大简化了数据结构和计算量;并能通过数值计算确定各污染物的权重系数,避免了主观随意性。文中的分析方法缺点在于只能对数值类指标进行分析,若能进一步改进,并编成计算软件,则此分析方法在水环境质量管理方面会有更好的应用前景■
(作者单位:淮安市淮河水利建设工程有限公司 223400)
