新息优先累加灰色离散模型的构建及应用

周伟杰，张宏如，党耀国，王正新

(1.常州大学商学院, 江苏 常州 213164；2. 南京航天航空大学经济与管理学院, 江苏 南京 211006；3.浙江财经大学经济学院，浙江 杭州 310018)

新息优先累加灰色离散模型的构建及应用

周伟杰1，张宏如1，党耀国2，王正新3

(1.常州大学商学院, 江苏 常州 213164；2. 南京航天航空大学经济与管理学院, 江苏 南京 211006；3.浙江财经大学经济学院，浙江 杭州 310018)

根据灰色新息优先利用思想，定义新的累加生成，与灰色离散模型结合，构建出新息优先累加生成的灰色离散模型(NIPDGM(1,1))。在四种误差准则下，给出了参数优化方法。进一步利用数值模拟，研究NIPDGM(1,1)模型在不同误差最小化下对信息的重视程度，分析表明在序列累加生成过程中，四种优化形式对信息的重视较为一致。在实证部分，以高速公路软土路基沉降以及江苏省能源消费问题为例，分析NIPDGM(1,1)模型的建模精度，结果表明：在NIPDGM(1,1)实证模型中，不同误差优化方式对信息的重视程度与数值实验结论相符；与GM(1,1,t2)、反向累加GOM(1,1)、倒数累加GRM(1,1)、GM(1,1)、DGM(1,1)、无偏GM幂模型相比，NIPDGM(1,1)对路基沉降的建模精度更优；与RBF神经网络、灰色累加生成RBF神经网络(GRBF)、支持向量机(SVM)、灰色累加生成支持向量机(GSVM)相比，NIPDGM(1,1)对能源消费的模拟误差大些，但预测误差更小，表明新模型具有更好的泛化能力。

新息优先；累加生成；NIPDGM(1,1)；误差准则

1 引言

预测是指在现有信息的基础上，利用一定的方法来研究事物发生的内在规律，以此预估事物将来发生的趋势，它是人类社会生活中一个重要环节。一般而言，给定一条数据序列，可以通过计量经济学、时间序列模型、神经网络、支持向量机学习等方法对数据建模预测，但这些方法建模对样本个数有一定要求，而在实际问题中，由于采样成本、调查方式等其它原因，获得数据量较少，或存在遗漏，用上述方法解决这类问题就显得较为薄弱。对此，我国学者邓聚龙[1]于1982年创立了灰色系统理论，以解决这类“贫信息”不确定系统。其中，灰色预测理论是灰色系统理论一个重要组成部分。其主要思想是：考虑到原始序列随机性对建模干扰，灰色预测理论通过序列累加生成，挖掘序列内在规律，建立微分与差分相结合的灰色预测模型，对系统未来变化进行预测。由此，序列累加生成是灰色信息挖掘、系统建模的一个关键步骤[2]。

目前有关灰色累加生成的文献主要有两个研究方面：1)累加生成思想与其它模型的集成。樊春玲等将灰色累加生成与RBF神经网络相结合，提出灰色径向基神经网络模型，实证表明新模型在建模精度与算法收敛速度方面得到改进[3]。Liu Lisang等[4]将RBF神经网络也与灰色累加生成结合，构建出GMRBF(2,1)模型，并应用于船舶运载能力预测，与原模型相比，GMRBF(2,1)模型有更好的预测精度。唐万梅[5]根据灰色预测理论中灰色累加生成的优点，将其与支持向量机(SVM)结合，构建出灰色支持向量机，实例结果证明了新模型的有效性。与唐万梅的构建思路相似，Xu Sheng等[6]也构建了基于遗传算法优化的灰色支持向量机，并将其应用于专利申请量预测，取得较高的建模精度。章杰宽[7]将灰色累加后的序列通过GM(1,N)模型映射到BP神经网络，并在遗传粒子群混合算法下构建出新型灰色神经网络模型，新模型在日本入华旅客数量预测实例中取得较好的建模精度。于志军等[8]将灰色累加生成后的序列，通过GM(1,N)模型与神经网络结合，构造出GNNM(1,N)模型，并应用于股市收益率预测，根据误差序列存在的ARCH效应，对误差序列用ARMA-EGARCH建模，使其预测精度相对于校正前提高了9.3%[8]。2)灰色累加生成技术的拓展。相应于传统灰色累加生成方式，宋中民和邓聚龙[9]提出了反向累加生成，在此基础上构建了GOM(1,1)模型。杨保华和张忠泉[10]定义倒数累加生成，并建立了GRM(1,1)模型。曾祥艳和肖新平[11]引入累积法，解决了GM(2,1)模型参数估计过程中矩阵求逆的病态性问题，并认为累积法GM(2,1)模型值得进一步推广。肖新平等[12]将累加生成形式矩阵化，定义具有下三角矩阵形式的累加生成，依此建立广义累加灰色预测控制模型，并说明GM(1,1)模型、跳跃模型等是该模型的特殊形式。Wu Lifeng等[13-14]为了使灰色模型解的扰动界变小，提出了分数阶累加方法，并与现有的灰色模型进行结合，得到较原有模型更好的预测效果。Ma Min和Wong[15]根据时尚消费品零售的季节特征，构建了具有周期效应的灰色累加生成，并与灰色离散预测模型相结合，提出了灰色季节(周期)离散模型，应用于高端、中端、一般时尚消费品的预测中，取得了较高的预测精度。

从以上文献可以看出，目前累加生成主要从数据特点、解的稳定性来构建，与灰色系统内在公理思想结合较少。为此，本文根据灰色系统公理中的新息优先利用原理，利用指数加权平均法特点，定义带有参数形式的累加生成，并与灰色离散模型结合，建立灰色新息优先累加灰色离散模型(New Information Priority Accumulated Grey Discrete Model,简记为NIPDGM(1,1))。根据多种判别准则，给出参数优化步骤，并研究了参数寻优的稳定性，最后将模型应用于高速公路软土路基沉降以及江苏省能源消费预测，以此检验模型建模效果。

2 新息优先累加灰色离散模型构建

2.1 模型构建

定义 1设X(0)为非负序列，X(0)=(x(0)(1),x(0)(2),…,x(0)(n))，令:

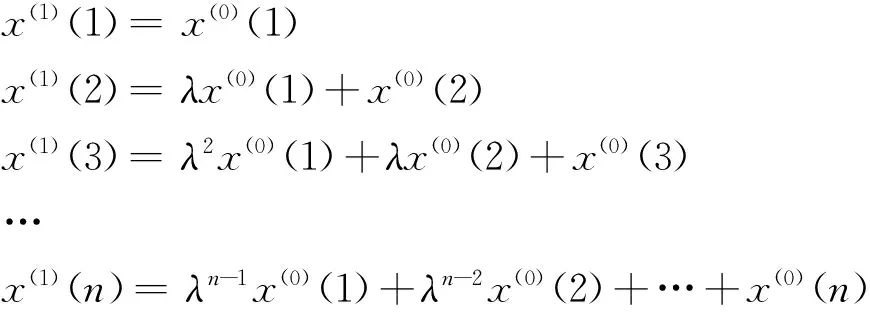
(1)

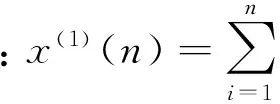
定义 2设X(0)为非负序列，X(0)=(x(0)(1),x(0)(2),…,x(0)(n))，取:

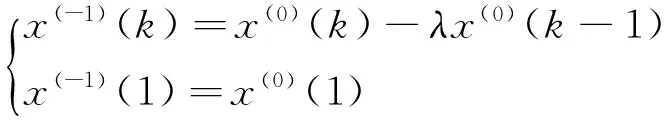
k=2,3,…,n，λ∈(0,1)

(2)

则称X(-1)=(x(-1)(1),x(-1)(2),…,x(-1)(n))为X(0)的一次新息优先累减生成序列(1-NIPIAGO)。

易知，新息优先累加、累减生成是互逆运算，有：

定义3 设X(0)为非负序列，X(0)=(x(0)(1),x(0)(2),…,x(0)(n))，X(1)为其一次新息优先累加生成序列，称x(1)(k+1)=β1x(1)(k)+β2为新息优先累加灰色离散模型(NIPDGM(1,1))。

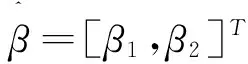
则模型x(1)(k+1)=β1x(1)(k)+β2的最小二乘估计参数序列满足：

(3)

那么有：(1)取x(1)(1)=x(0)(1)，则递推函数为：

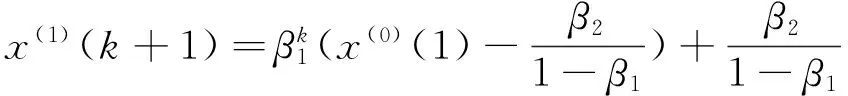
(4)

(2)还原值：

(5)

证明：根据文献[17]可得式(4)，再由一次新息优先累减生成可得式(5)。

2.2 建模机理分析

定义1在原始信息X(0)向X(1)累加生成的过程中，运用了指数加权累加的方式，当0<λ<1时，越邻近现在时刻的信息赋予权重越大，越远的信息按照指数衰减其权重越小。在x(1)(k)计算中，x(0)(i)的权重是前一个的x(0)(i-1)的λ-1倍，因此，新定义的累加生成符合新信息优先利用公理；当λ=0时，X(1)=X(0)；当λ=1时候即为传统累加生成算子。其中，λ可认为是区间灰数，在建模预测的过程中，根据模型对系统新旧信息内在关系的挖掘，得到一个合适解，使模型更加适应事物本身发展规律。同时，也可以看出，如果传统累加生成出现“过累加(指的是经过一次累加，由于累加的作用过强，数据建模精度反而降低)”情形，只要λ取值恰当，新累加生成在一定程度上可以解决此类问题。

2.3 参数的确定

从新息优先累加生成的灰色离散模型(NIPDGM(1,1))构造来看，若λ确定，β1、β2可以通过最小二乘计算出来，考虑到模型的非线性特点，参数的确定可以通过目标误差最小的非线性优化模型求解。目前，在预测模型参数优化求解时，主要有四种目标误差最小原则：平均误差平方L1、平均绝对误差L2、平均相对误差平方L3、平均绝对百分误差L4，

研究者可以根据实际问题需要选择误差形式来建模，NIPDGM(1,1)的参数求解过程如下：

minLi(i=1,2,3,4)

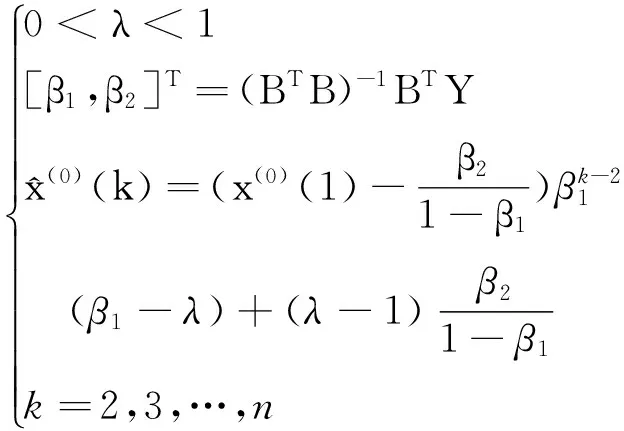
(6)

上述模型可以通过一些智能算法如遗传算法(GA)、粒子群算法(PSO)、差分演进算法(DE)等来计算，由于智能算法只需确定一个参数λ，参数求解的稳定性较高，同时，在本文实证和数值模拟时，发现利用GA、PSO、DE算法计算出的λ几乎相等，为此，本文只给出用GA算法得出的结果。

2.4λ取值分析

NIPDGM(1,1)模型是以新息优先为出发点，x(1)(k)计算时对新旧信息的重视程度取决于λ值。因此，在参数优化不同标准下，对信息重视程度的影响需要做进一步分析。根据灰色离散模型对不同数据类型建模优劣的特点，随机产生增速不同、长度不同的序列进行分析，具体做法如下：

步骤1.令x(1)=1，x(i)=a·x(i-1)，a～U(1,1.5)，即a由均匀分布[1,1.5]的随机产生，由此反复迭代产生n个数据，则X=(x(1),x(2),…,x(n))。

步骤2.按照步骤1，分别产生数据长度n=4,5,6,7,8,9的序列各1000组。

步骤3.利用NIPDGM(1,1)模型，分别对数据长度不同的1000组数据每条序列建模，在四种误差最小标准下，得到四种不同的λ：λ1、λ2、λ3、λ4，令

Δλ=max{λi|i=1,2,3,4}-min{λi|i=1,2,3,4}

(7)

步骤5.令a～U(1.5,2)，重复步骤.1-4。结果见图1和2。

从图1和2可以看出，无论a～U(1,1.5)还是a～U(1.5,2)，Δλ落在[0,0.1]的个数是最多的(Δλ越小，表明在不同参数优化标准下，对新旧信息

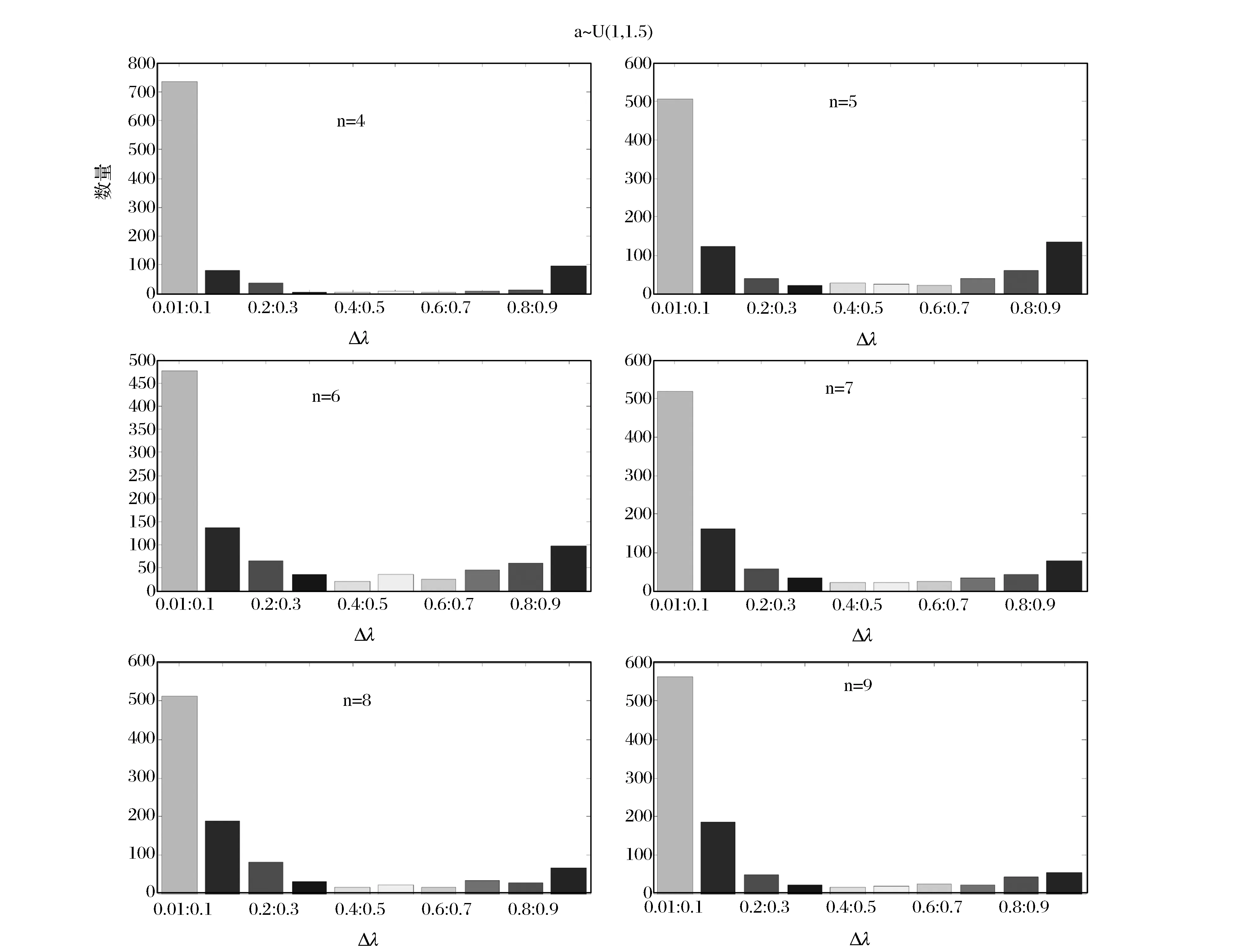
图1 不同数据长度下a～U(1,1.5)时{Δλ}柱状图

重视程度影响越小)，均超过500个，落在[0.1,0.2]的个数次之。具体来看，当a～U(1,1.5)时，即数据增速在[1,1.5]区间时，数据长度n=5的Δλ落在[0,0.1]的个数最小，而n=4的最多；数据长度n=8和n=9落在[0.1,0.2]的个数均接近200个。当a～U(1.5,2)时，即数据增速较大时，Δλ落在[0,0.1]的个数均超过600个，并且除了n=5外，Δλ落在[0,0.1]的个数随数据长度n的增加而增加，当n=9时，其个数接近900。以上分析说明，由四种误差最小化计算出的λ值较为接近，稳定性较好，从而表明在NIPDGM(1,1)模型的序列累加生成中，四种优化形式对信息的重视程度较为一致，参数λ受不同误差的影响较小。

3 实例分析

3.1 高速公路软土路基沉降建模分析

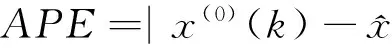
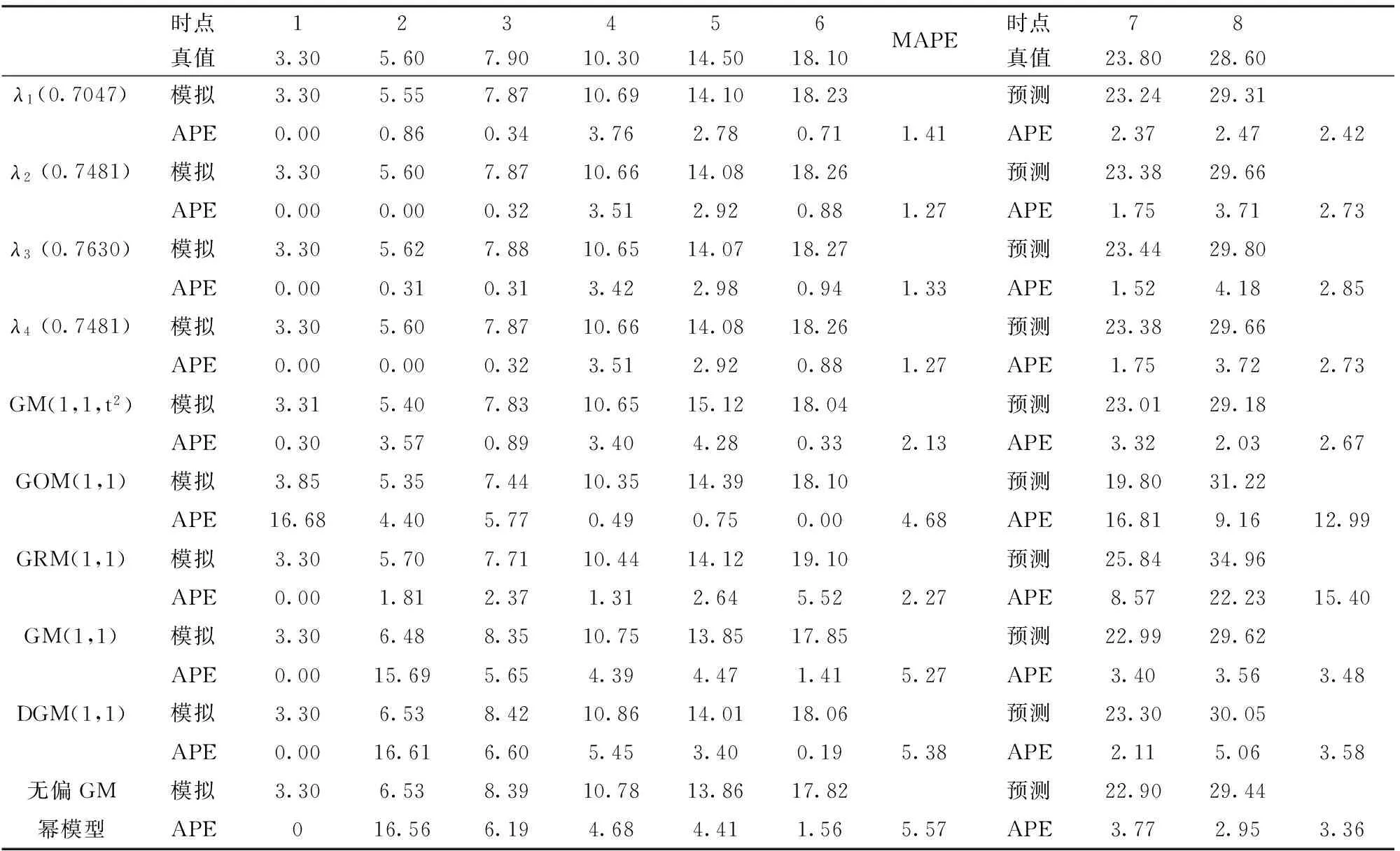
表1为某高速路观测点软土地基沉降建模结果，从λ1、λ2、λ3、λ4值来看，四者相差不大，λ2与λ4相同，Δλ为0.0583，表明误差优化方式并不影响累加过程中的信息权重，与2.4节数值实验的结论一致。从NIPDGM(1,1)-λi模型的模拟值和预测值来看，与实际观测值十分接近。从绝对百分误差(APE)来看，在模拟阶段，四种NIPDGM(1,1)模型的误差均小于4%，而其余模型都有超过4%的时点模拟误差：GM(1,1,t2)模型在模拟第五个时点时，误差为4.28%；GOM(1,1)模型前三个时点的模拟值误差均超过4%，其中第一个时点的误差达到16.68%；GRM(1,1)模型第五个时点的模拟误差为5.52%；GM(1,1)模型除在第一个与第五个时点的误差小于4%，其余均超过4%，其中第二个时点的模拟误差达到15.69%；DGM(1,1)模型在第三、四、五个时点的模拟误差超过4%，其中在第二个时点的模拟误差达到16.61%；与DGM(1,1)类似，无偏GM幂模型在第三、四、五时点的模拟误差也超过4%，第二个时点的模拟误差也到达16%。在预测阶段，除了NIPDGM(1,1)-λ2模型在预测第八个时点时误差为4.18%，其余NIPDGM(1,1)-λi模型的时点预测误差均小于4%，其中NIPDGM(1,1)-λ1模型的时点预测误差只有2.37%和2.47%。GM(1,1,t2)模型的时点预测误差分别为3.32%、2.03%。GOM(1,1)模型的两个时点预测误差达到16.81%与9.16%，预测值与真值相差较远。GRM(1,1)模型的预测误差为8.57%和22.23%，也与真值相差较大。GM(1,1)模型的时点预测误差分别为3.4%和3.56%。DGM(1,1)模型的时点预测误差为2.11%和5.06%。无偏GM幂模型的预测误差也只有3.77%与2.95%。NIPDGM(1,1)-λi模型、GM(1,1,t2)模型、GM(1,1)模型、DGM(1,1)模型、无偏GM幂模型得出的预测值与真值较为接近。从平均绝对百分误差(MAPE)来看，在模拟阶段，四种NIPDGM(1,1)-λi模型误差均小于2%，其余模型误差都大于2%，无偏GM幂模型误差最大，达到5.57%。在预测阶段，四种NIPDGM(1,1)-λi模型与GM(1,1,t2)模型误差均小于3%，其中NIPDGM(1,1)-λ1模型预测误差最小，仅有2.42%；其余模型误差都超过3%，GRM(1,1)模型误差最大，达到15.4%。总的来说，NIPDGM(1,1)-λi模型建模精度比GM(1,1,t2)、GOM(1,1)、GRM(1,1)、GM(1,1)、DGM(1,1)、以及无偏GM幂模型更优。

时点123456真值3.305.607.9010.3014.5018.10MAPE时点78真值23.8028.60λ1(0.7047)模拟3.305.557.8710.6914.1018.23预测23.2429.31APE0.000.860.343.762.780.711.41APE2.372.472.42λ2(0.7481)模拟3.305.607.8710.6614.0818.26预测23.3829.66APE0.000.000.323.512.920.881.27APE1.753.712.73λ3(0.7630)模拟3.305.627.8810.6514.0718.27预测23.4429.80APE0.000.310.313.422.980.941.33APE1.524.182.85λ4(0.7481)模拟3.305.607.8710.6614.0818.26预测23.3829.66APE0.000.000.323.512.920.881.27APE1.753.722.73GM(1,1,t2)模拟3.315.407.8310.6515.1218.04预测23.0129.18APE0.303.570.893.404.280.332.13APE3.322.032.67GOM(1,1)模拟3.855.357.4410.3514.3918.10预测19.8031.22APE16.684.405.770.490.750.004.68APE16.819.1612.99GRM(1,1)模拟3.305.707.7110.4414.1219.10预测25.8434.96APE0.001.812.371.312.645.522.27APE8.5722.2315.40GM(1,1)模拟3.306.488.3510.7513.8517.85预测22.9929.62APE0.0015.695.654.394.471.415.27APE3.403.563.48DGM(1,1)模拟3.306.538.4210.8614.0118.06预测23.3030.05APE0.0016.616.605.453.400.195.38APE2.115.063.58无偏GM模拟3.306.538.3910.7813.8617.82预测22.9029.44幂模型APE016.566.194.684.411.565.57APE3.772.953.36

注：表中λi表示NIPDGM(1,1)-λi模型，表2，表3中的λi含义与此相同。

3.2 江苏省能源消费建模分析

经济的快速发展，离不开对能源的需求，由于江苏省自然资源较少，能源消费主要依靠外来投入。长期以来，能源短缺问题一直困扰江苏经济可持续发展。考虑到能源消费系统具有复杂性、非线性、不确定等特点，其影响因素也较多，同时相关数据收集比较困难，转化也缺乏统一标准，因此属于“部分信息已知，部分信息未知”，“小样本”、“贫信息”的不确定性系统。为此，可以用灰色预测理论对其建模分析。以江苏省2001年至2010年的能源消费数据为建模数据，2011和2012年的数据作为预测数据，建立多种模型：RBF神经网络模型(简记为RBF)[19-20]、基于灰色累加生成的RBF神经网络模型(简记为GRBF)[3-4]、支持向量机模型(简记为SVM)[21-23]、基于灰色累加生成的SVM模型(简记为GSVM)[5-6]，以对比分析新模型的建模精度。在建模时，如例3.1考虑了GM(1,1,t2)、倒数累加GM(1,1)、反向累加GOM(1,1)模型，结果发现模拟值与预测值与实际值偏离较大，在精度比较时省略这部分内容。RBF、GBRF、SVM、GSVM的模型参数设置如下：

① RBF：考虑到所给的时间序列为单个序列，根据数据长度，设相空间的维数有3种，分别为5、4、3；建模均方误差范围为[0,0.1]；径向基函数的扩展速度范围为[100,10000]；在上述范围内，根据建模结果进行优化选择。

②GRBF：考虑到数据需要先累加生成，为了避免数据量级相差过大使建模出现失真，对数据进行压缩变换，最后对建模结果逆向转换，其余参数选择如RBF。

③SVM：考虑到建模数据特征，对数据进行压缩变换；选ε-SVR模型(参数为0.1)，根据交叉验证法，寻找最优回归参数c与g。相空间的维数分别为5、4、3。

④GSVM：数据变换及参数选择如SVM。

表2 为江苏省能源消费在不同模型下的建模结果，考虑本例采用模型较多，在表2中没有将绝对百分误差(APE)和平均绝对百分误差(MAPE)计算在内，用表3与图3分析建模精度。从中可以看出：对于NIPDGM(1,1)-λi模型，不同准则下的λi(i=1,2,3,4)较接近，Δλ=0.107，表明在进行数值拟合时，四种优化方式对信息重视程度比较一致，验证了2.4节的结论。四种NIPDGM(1,1)-λi模型的模拟值、预测值与江苏省实际能源消费都比较接近；对于RBF、GRBF、SVM、GSVM模型，在不同相空间维数建模下，其模拟值比较接近真值，但预测值有的与实际值相差较大，如RBF5(5指的是相空间维数)、GRBF5、SVM3、GSVM3模型对2011年的预测，以及RBF4、GRBF5、GRBF4、GRBF3、SVM4、SVM3、GSVM3模型对2012年的预测。对于GM(1,1)、DGM(1,1)、无偏GM幂模型，在模拟阶段与真值较为接近，但在预测阶段，其数值与江苏省实际能源消费相差较大，如三者在2012年的预测在33000万吨左右，而实际值只有28850万吨。表3为各个模型的模拟和预测平均绝对百分比误差。可以看出，对于NIPDGM(1,1) -λi模型，不同准则下的模拟平均绝对相对误差在2.3%左右，预测误差在0.5%左右；而对于RBF、GRBF、SVM、GSVM模型，在模拟阶段，平均绝对百分误差低于2%的有8种，但在预测阶段， 12种结果中，误差最低也高于2%，其中GRBF4、GSVM5、GSVM3模型的预测误差在10%以上，说明在江苏省能源消费建模中，此类模型的模拟效果较好，但其泛化能力不如NIPDGM(1,1)模型。在GM(1,1)、DGM(1,1)、无偏GM幂模型建模下，模拟误差在7%左右，预测误差均大于10%，表明无论在模拟阶段还是在预测阶段，这三类模型的建模精度不及NIPDGM(1,1) -λi模型。在图3中，根据相空间维数的维数设定，以NIPDGM(1,1) -λ1、RBF3、GRBF3、SVM4、GSVM4建模效果较好的5个模型，做出2005-2012年的模拟值和预测值图形。可以看出，就江苏省能源消耗2011年预测值来看，NIPDGM(1,1) -λ1、RBF3、GRBF3、SVM4、GSVM4模型得出的结果均与真实值比较接近，而对于2012年的预测值，NIPDGM(1,1) -λ1模型表现更优。总的来说，在江苏省能源消费建模中，尽管NIPDGM(1,1) -λi模型的模拟精度不是最优的，但是其预测效果是最好的。

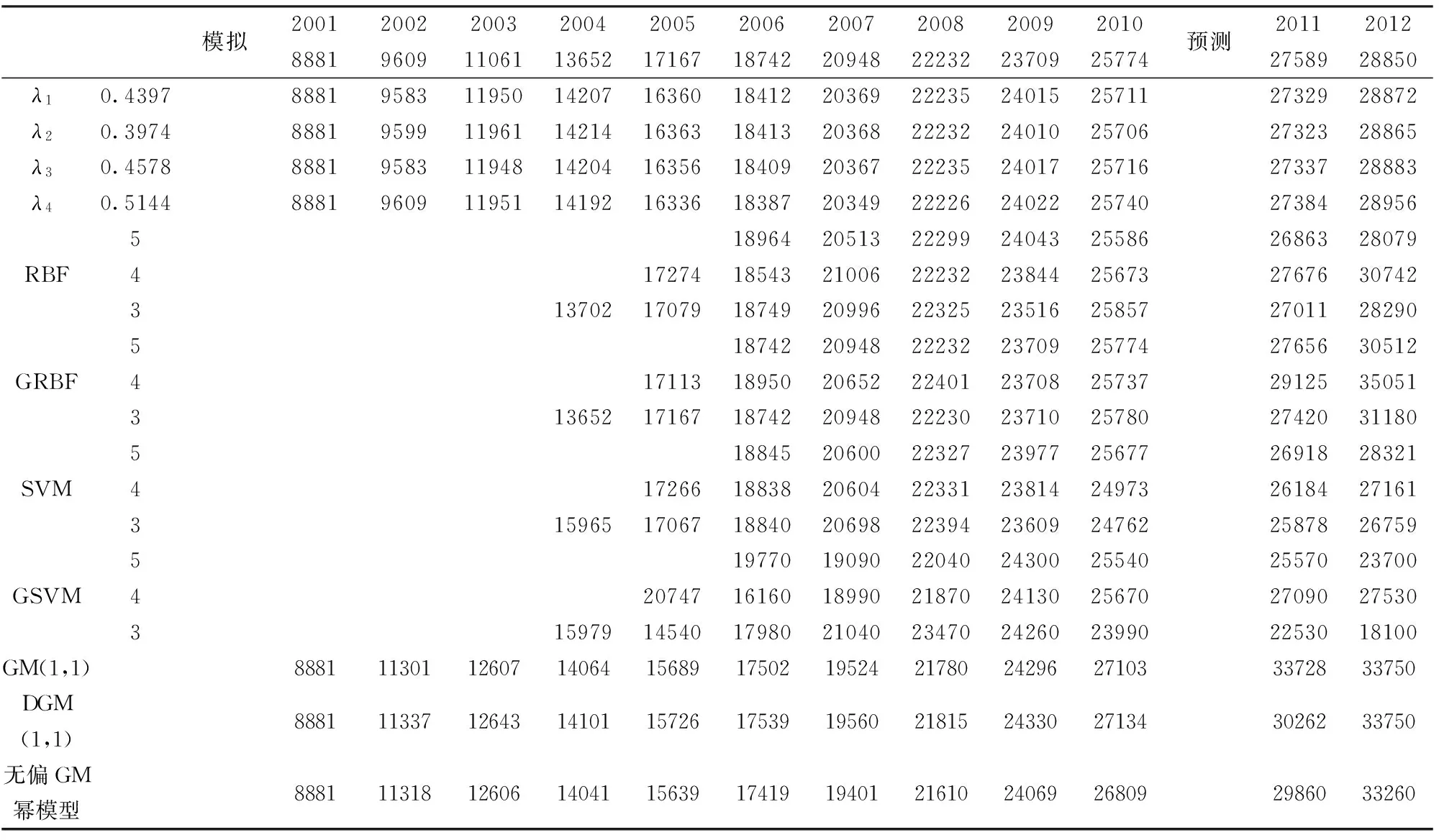
表2 2001～2012年江苏省能源消费建模分析(单位：万吨标准煤)

注：数据来源于江苏统计年鉴，表中空缺是由一维序列构造相空间时产生的，可令为原值补上。

表3 不同模型模拟与预测平均绝对相对误差(单位：%)

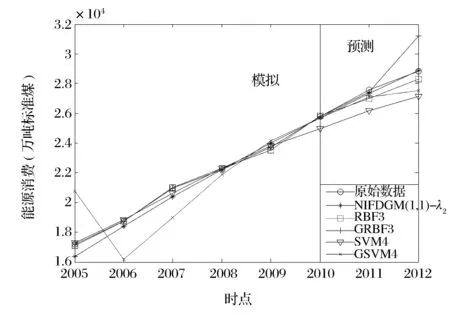
图3 江苏省能源消费建模分析

4 结语

本文受灰色系统新息优先利用公理启发，按照指数加权的方式，定义带有参数形式的累加生成公式，进一步与灰色离散模型结合，建立了新息优先累加生成的灰色离散模型(NIPDGM(1,1))，并在四种误差最小化准则下，给出了参数优化步骤。通过数值分析以及实证检验，得出在NIPDGM(1,1)模型中，误差准则的选取并不影响累加生成参数大小，四种优化形式对序列信息重视程度较为一致这一结论。利用NIPDGM(1,1)模型对高速公路软土路基沉降建模，并用一些常见灰色模型进行对比，发现四种NIPDGM(1,1) -λi模型的时点模拟及预测误差绝大部分小于4%(仅NIPDGM(1,1) -λ2模型预测第八个时点的误差超过4%)，模型精度高于其余对比模型。此外，用NIPDGM(1,1)模型、机器学习模型及常见灰色模型对江苏省能源消费建模，结果表明：与常见灰色模型相比，NIPDGM(1,1)模型的模拟及预测精度要更高些；与RBF、GRBF、SVM、GSVM模型相比，NIPDGM(1,1)模型的模拟误差较大，但其预测精度更高，说明NIPDGM(1,1)模型的泛化能力更强。

从新息优先累加生成算子来看，更注重对新信息规律的挖掘，突出了新信息在建模时的贡献，为此，基于新息累加生成的灰色模型适合近期变化较大、有新特征的系统行为序列，如我国经济由高速发展转到中高速发展的新常态，地区生产总值增长速度已经降低，有了新特征，可以用本文提出的模型建模；由于国家对环境治理的新要求，煤炭消费出现了降低，也可以用本文模型。进一步的工作是将新累加生成与其它灰色预测模型相结合，研究是否能改善其它灰色模型的建模精度，从而完善灰色模型体系。

[1] Deng Julong. Control problems of grey system [J]. System & Control Letter, 1982, 1(5):288-294.

[2] Liu Sifeng, Lin Yi. Grey systems theory and applications [M].Berlin-Heidelburg.Springer, 2010.

[3] 樊春玲, 张静, 金志华, 等. 一种新型的灰色 RBF 神经网络建模方法及其应用[J]. 系统工程与电子技术, 2005, 27(2): 316-319.

[4] Liu Lisang,Peng Xiafu, Zhou Jiehua. Ship rolling prediction based on gray RBF neural network [J]. Applied Mechanics and Materials, 2011, 48-49: 1044-1048.

[5] 唐万梅. 基于灰色支持向量机的新型预测模型[J]. 系统工程学报, 2006, 21(4): 410-413.

[6] Xu Sheng, Zhao Huifang, Lv Xuanli. A Grey SVM based model for patent application filings forecasting[C]//Proceealings of IEEE International Conference on Fuzzy Systems,Hongkong,China,June 1-6,2008. 2008: 225-230.

[7] 章杰宽. 智能组合预测方法及其应用[J].中国管理科学, 2014, 22(3):26-33.

[8] 于志军, 杨善林, 章政,等. 基于误差校正的灰色神经网络股票收益率预测[J]. 中国管理科学, 2015, 23(12):20-26.

[9] 宋中民, 邓聚龙. 反向累加生成及灰色 GOM (1,1) 模型[J]. 系统工程, 2001, 19(1): 66-69.

[10] 杨保华, 张忠泉. 倒数累加生成灰色 GRM (1, 1) 模型及应用[J]. 数学的实践与认识, 2003, 33(10): 21-26.

[11] 曾祥艳, 肖新平. 累积法 GM (2, 1) 模型及其病态性研究[J]. 系统工程与电子技术, 2006, 28(4): 542-544.

[12] 肖新平, 刘军, 郭欢. 广义累加灰色预测控制模型的性质及优化[J]. 系统工程理论与实践, 2014, 34(6): 1547-1556.

[13] Wu Lifeng, Liu Sifeng, Yao Ligen, et al. Grey system model with the fractional order accumulation [J]. Communications in Nonlinear Science and Numerical Simulation, 2013,18(7):1775-1785.

[14] 吴利丰, 刘思峰, 刘健.灰色 GM (1, 1) 分数阶累积模型及其稳定性[J]. 控制与决策, 2014, 29(5): 919-924.

[15] Xia Min, Wong W K. A seasonal discrete grey forecasting model for fashion retailing[J]. Knowledge-Based Systems, 2014, 57: 119-126.

[16] 钱吴永, 党耀国, 刘思峰.含时间幂次项的灰色 GM (1, 1, tα) 模型及其应用[J]. 系统工程理论与实践, 2012, 32(10): 2247-2252.

[17] 谢乃明, 刘思峰.离散GM(1,1)模型与灰色预测模型建模机理[J]. 系统工程理论与实践, 2005, 25(1):93-99.

[18] 王正新, 党耀国, 练郑伟. 无偏GM(1,1)幂模型其及应用[J]. 中国管理科学, 2011, 19(4):144-151.

[19] Broomhead D S, Lowe D. Radial basis functions, multi-variable functional interpolation and adaptive networks[R]. Royal Signals and Radar Establishment, 1988.

[20] Reiner P, Wilamowski B M. Efficient incremental construction of RBF networks using quasi-gradient method [J]. Neurocomputing, 2015,150(B):349-356.

[21] Cortes C, Vapnik V. Support-vector networks [J]. Machine Learning, 1995, 20(3): 273-297.

[22] Lingras P, Butz C J. Rough support vector regression [J]. European Journal of Operational Research, 2010, 206(2): 445-455.

[23] Lapin M, Hein M, Schiele B. Learning using privileged information: SVM+ and weighted SVM [J]. Neural Networks, 2014,(53):95-108.

New Information Priority Accumulated Grey Discrete Model and Its Application

ZHOU Wei-jie1, ZHANG Hong-ru1, DANG Yao-guo2, WANG Zheng-xin3

(1. Business college, Changzhou university, Changzhou 213164,China;2. College of Economics and Management, Nanjing University of Aeronautics and Astronautics, Nanjing 211106,China;3. School of Economics, Zhejiang University of Finance & Economics, Hangzhou 310018,China)

The accumulated generation is an important part of grey prediction model, which helps mine information and finds the rule in sequence. According to the axiom of new information priority using in grey systems, new accumulated generation operator with parameter is defined, and then the new information priority accumulated grey discrete model (NIPDGM (1,1)) is constructed. Based on four kinds of error minimization criterions (mean squared error, mean absolute error, mean relative squared error, and mean absolute percentage error), the parameters optimization steps are presented. Through numerical simulating, the information weight in NIPDGM (1,1) model with different error criterions is studied. The result shows that the four kinds of optimization form for information weight are almost identical in sequence accumulated generation process. In the empirical analysis, expressway soft soil roadbed settlement and energy consumption problems in Jiangsu province are taken as examples, and the NIPDGM (1,1) modeling is used for two cases. In order to compare the modeling accuracy of new model, other grey model and some artificial intelligence models are also adopted for two cases, such as grey model(GM (1,1)), grey opposite model (GOM(1,1)), grey reciprocal model(GRM(1,1)), discrete grey model(DGM(1,1)), radial basis function(RBF) neural network, support vector machine (SVM) and so on. The results show that the information weights (or the parameter in accumulated generation) are not subjected to the different error minimization methods, which is consistent with the numerical simulating experiment. Compared with GOM (1,1) model, GRM(1,1)model, GM(1,1) model, DGM(1,1)model, grey model with time power (GM (1,1, t2)), and unbiased GM (1,1) power model, NIPDGM (1,1) model has a higher modeling precision in simulating and forecasting period for roadbed settlement. Among RBF neural network, grey accumulation generation RBF neural network (GRBF), support vector machine (SVM), grey accumulated generation support vector machine (GSVM) and NIPDGM (1,1) model for energy consumption modeling, the NIPDGM (1,1) model has a lager error in simulating period, but the smaller error in forecasting period, which indicates that the NIPDGM (1,1) model exhibits better generalization ability. The new accumulated generation operator can also be combined with other grey model, so as to enhance the model accuracy.

new information priority; accumulated generation; NIPDGM(1,1) model; error criterion

1003-207(2017)08-0140-09

10.16381/j.cnki.issn1003-207x.2017.08.015

2016-03-08；

2016-10-24

国家自然科学基金面上资助项目(71371098,71571157,71101132)；国家社科基金重点项目(16ASH005)

张宏如(1973-),男(汉族),安徽安庆人,常州大学商学院教授,博导,研究方向：灰色系统、人力资源，E-mail:cdjr131@163.com.

N941.5

A