中国股市收益率与成交量动态关系的研究
——基于工具变量的分位数回归(IVQR)模型
2017-09-15任燕燕李劭珉
任燕燕,李劭珉
(山东大学经济学院,山东 济南 250100)
中国股市收益率与成交量动态关系的研究
——基于工具变量的分位数回归(IVQR)模型
任燕燕,李劭珉
(山东大学经济学院,山东 济南 250100)
基于分位数回归(QR)模型分析了不同分位水平下的收益率与成交量的关系,考虑到收益水平对成交量的影响,引入工具变量,构建IVQR模型,更加客观地分析了不同分位水平下成交量对收益率的作用。蒙特卡洛模拟结果表明IVQR估计比QR估计具有更小的偏差和更强的稳健性。实证分析结果表明条件收益率处于较高水平时与成交量正相关,且分位水平越高两者之间的相关性越大;条件收益率处于较低水平时与成交量负相关,且分位水平越低相关性越大;多数分位水平下成交量对收益率的影响并没有较大的差异。同时结果还表明工具变量的分位数回归模型能较好地处理模型中的内生性问题。
收益率;成交量;QR模型;IVQR模型
1 引言
作为金融市场中两个重要的衡量指标,市场价格与交易量是微观市场研究的核心要素,涵盖了所有的市场行为和市场信息。对于二者关系的刻画,是理解金融市场波动的关键。因而股市收益率与成交量的关系,即量价关系研究成为金融学领域的研究热点。
国外对量价关系的研究较早,Crouch[1]在1970年发现无论指数还是个股,其收益的绝对值与交易量都呈现同期正相关关系。Karpoff[2]研究发现成交量与股票收益率变化绝对值呈现一种正相关关系。Lamoureux和Lastrapes[3]把交易量加入到GARCH 模型的条件方差方程中,发现对价格波动有很强的解释能力。Chen Gongmeng[4]用Granger检验研究九个国家的股价和交易量之间的动态关系,检测出了双向的因果关系。国内的研究起步较晚,但学者在各个方面都做了大量的工作,成果丰厚。在数据选择方面,郭梁和周炜星[5]通过高频数据研究了中国股市个股的成交量与价格变化之间的关系,得出低成交量对应的反常负相关量价关系的产生原因在于市场摩擦的结论。在模型构建方面,吴冲锋等人[6]提出基于交易量进程的股价动力学分析方法,将交易量结合进资产的价格序列之中,得到了较好的拟合结果。吴秋芳等人[7]使用EGARCH 模型和BP 神经网络对中国股市的量价关系进行了实证研究,发现非预期成交量与股市波动性之间存在较强的正相关关系。卢英和刘晓艳[8]发现Joe Copula模型能够较好地描述收益率与成交量之间的相关程度,并且准确捕捉二者的相关模式。在估计参数方面,陈怡玲和宋逢明[9]用广义差分方法,得出成交量与正的价格变动正相关,与负的价格变动负相关。田大伟和金泰一[10]引入Robust方法估计参数,结果表明收盘收益率和开盘收益率与交易量正相关,且Robust方法比OLS方法更加肯定了这种正相关关系的存在。我国学者还从其他角度对量价关系进行了研究,如翟爱梅[11-12]等人基于市场参与者非理性行为假设,从供给需求分析出发,研究股票市场量价关系,发现成交量和成交价格变动的绝对值正相关。徐加根等人[13]利用技术分析指标描述股票短期涨跌趋势,发现上涨放量有助于抬高股票收益率.下跌放量则会压低股票收益率。
对量价关系的研究最常用的是线性回归模型,分析得到的是成交量与收益率均值之间的关系,容易忽略收益率较高时和较低时的重要信息。为了充分利用收益率分布的特征,分位数回归的方法被越来越多的应用到金融领域,林德钦[14]采用分位数回归模型对上证综合指数的收益率与成交量关系进行分析,发现在收益率左端,收益率与成交量呈负相关,在收益率右端,两者存在正相关关系。利用传统的分位数回归方法得到的结果可以反映成交量与不同分位水平下的收益率的相关性,但由于收益率的分位水平会影响成交量(一般表现为收益率的分位水平越高,成交量越大),导致模型中存在内生性,这样传统方法估计的系数中包含了分位水平对成交量影响的成分,不能反映成交量对收益率客观的影响作用。为了解决传统分位数回归模型中的内生性问题,论文引入前一期的成交量作为工具变量,构建IVQR模型[15],更加准确地量化成交量对不同分位水平下的收益率的作用。
本文通过蒙特卡洛模拟方法比较了QR估计与IVQR估计的性质;利用沪深300指数的历史交易日数据,运用IVQR模型,验证了成交量对不同分位水平下我国股市收益率的作用差异。实证结果表明,与直接使用分位数回归的结果不同,引入工具变量后的分析结果显示成交量对大多数分位水平下的收益率影响较小。条件收益率处于中段或较高的分位水平时,成交量的增加会使股价上升,而条件收益率处于较低的分位水平时,成交量的增大会导致股价下跌。
文章的结构安排如下:第二部分介绍了研究方法;第三部分进行了蒙特卡洛模拟;第四部分描述了样本数据、实证结果与分析;第五部分总结全文。
2 模型构建
2.1 分位数回归模型
利用分位数回归模型研究不同分位水平τ下的收益率r与成交量q之间的关系。
分位数回归模型由Koenker和Bassett[16]首先提出,是研究被解释变量的不同分位点与解释变量关系的模型。与普通的均值回归相比,分位数回归模型可以全面地描述解释变量对被解释变量的影响,可以度量回归变量在分布上尾和下尾的影响,捕捉整个条件分布的特征,而且对模型中的随机扰动项不需要做任何分布的假定,这使得整个回归模型具有很强的稳健性。
论文构建的线性分位数回归模型为:
Qr(τ|q)=α(τ)+q·β(τ)
(1)
其中α((τ)为截距项,β(τ)为需要估计的斜率系数,Qr(τ|q):=inf{ξ:Fr(ξ|x)≥τ}表示随机变量r的第τ条件分位数。参数估计的方法为:
(2)
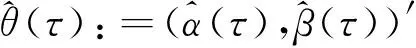
(3)
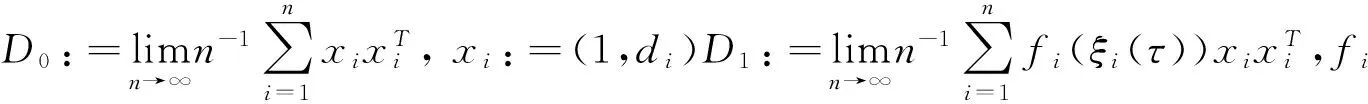
根据Skorohod表示理论,对于随机变量r,存在随机变量U~Uniform(0,1),使得r可以表示成r=Q(U)这种形式,其中Q(τ)表示r的第τ分位数(参见Durrett[19])于是,线性分位数回归模型还可以用另一种形式表示为:
r=α(U)+qβ(U),U|q~Uniform(0,1)
(4)
其中τα(τ)+qβ(τ)是τ的连续且严格的递增函数。随机变量U取值为τ时,α(τ)+qβ(τ)便是r在q已知条件下的第τ分位数,对应的回归系数β(τ)的估计仍用传统模型的估计方法即可。
2.2 IVQR模型
IVQR模型由Chernozhukov在2004年提出,解决了分位数回归模型中存在内生性问题时的参数估计问题。在模型r=α(U)+qβ(U)中,成交量q可能会受到收益率分位水平U的影响:分位水平U的值τ较大时,条件收益率处于较高的水平,那么投资者受追涨情绪的影响会增加投资,使得成交量q增加,这就是所谓的“势头效应”[14];分位水平U的值τ较小时,条件收益率处于较低的水平,受“羊群效应”的影响,投资者为避免更多的损失可能会纷纷卖掉手中的股票,从而出现在收益率尾端成交量非常大的现象[14]。q与U之间的相关性会导致模型中存在内生性,那么用传统的分位数回归方法估计的参数将不具有一致性,甚至与真实的β(τ)有较大的偏差。考虑到收益率水平对成交量的影响,本文在模型中引入工具变量,构建IVQR模型。工具变量要满足以下两个条件:与成交量q有关,且不受收益率水平U的影响。论文选取的工具变量为前一期的成交量,用z表示,其与现期成交量的样本相关系数为0.89,这表明它们之间有较强的相关性,而且前一期的成交量显然不会受到现期的收益率水平的影响。引入z后,构建的IVQR模型为:
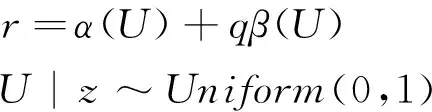
(5)
τα(τ)+qβ(τ)是τ的连续且单调递增函数,其中q与U相关,z为工具变量。
构建分位数函数(SQF)为:
Sr(τ|q)=α(τ)+qβ(τ)
(6)
由于事件{r≤Sr(τ|q)}等价于事件{U≤τ}得:
P[r≤Sr(τ|q)|z]=P[U≤τ|z]=τ
(7)
即P[r-Sr(τ|q)|z]=τ,也就是说0是随机变量r-Sr(τ|q)的第τ条件分位数。于是便有
(8)
那么问题转化为求合适的Sr(τ|q)使上述等式成立,为了简化计算令f(z)=z·γ,结合Sr(τ|q)=α(τ)+qβ(τ),则目标函数可表示为:
(9)
如果给定了β的值,那么α和γ的估计可用传统的分位数回归参数估计方法得到,即
(10)
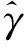
(11)
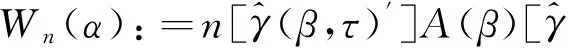
(12)
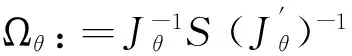
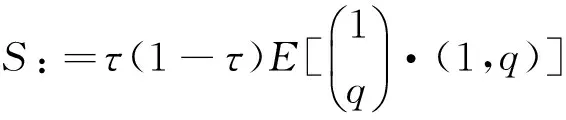
对参数的显著性检验可用Chernozhukov[20]提出的检验统计量。论文直接利用参数估计的渐近分布进行检验并求出参数的置信区间。
3 模拟比较
利用蒙特卡洛模拟方法比较QR估计和IVQR估计的性质,主要考察偏差(Bias)和均方误差(MSE)两个指标。
构造的模型为:

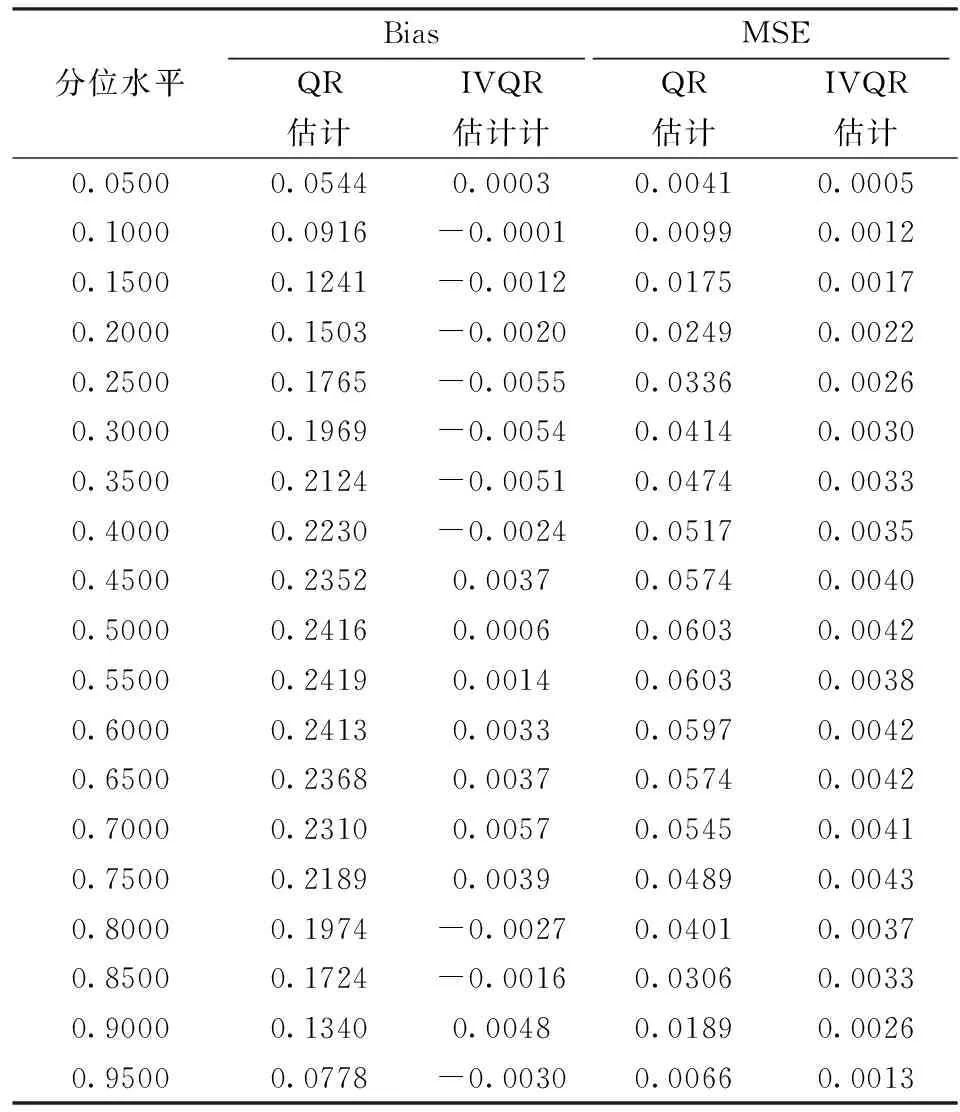
表1 两种估计的偏差和均方误差
通过表1可以发现,在各个分位水平上,利用QR进行参数估计有非常大的偏差,偏差甚至能达到一倍以上(在0.05分位水平上的斜率真实值为0.05,而QR估计的偏差为0.054);而IVQR估计的偏差非常小,大多数分位水平上的偏差不超过真实值的1%,而且均方误差也非常小,这表明IVQR估计比QR估计更有效且更稳健。为了更直观的显示结果,将表中的数据画在图1中。
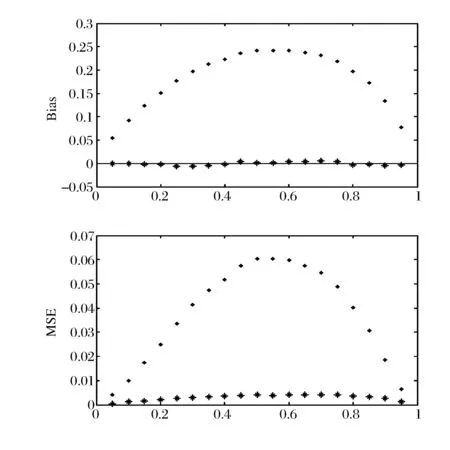
图1 两种估计的Bias和MSE
图1的上半部分图形是对两种估计偏差(Bias)的比较,下半部分图形是对两种估计均方误差(MSE)的比较。圆实点代表QR方法的结果,星号代表IVQR方法的结果。可以看出IVQR估计的偏差和均方误差非常接近于0水平线,表明IVQR估计同时具有较小的偏差和较强的稳健性;与之比较,QR估计的偏差和均方误差距离0水平线较远,并且以抛物线的形状展现,随着分位点的升高逐渐增大,在大约0.6分位点附近达到最高点后又逐渐变小,表明QR估计具有较大的偏差且稳健性较差。因此在实证分析中,利用IVQR估计的结果更加靠近真值,效果好于QR估计的结果。
4 实证分析
数据来源于Wind资讯客户端,所取样本为沪深300指数2005年4月28日到2014年4月16日共2200个交易日的收盘价和成交量的数据。
首先对数据进行处理,利用对数收益率进行计算,本期的收益率rt为本期收盘价pt与前期收盘价pt-1之比的对数,单位为百分比:rt=100×log(pt/pt-1);成交量qt单位为1010股。
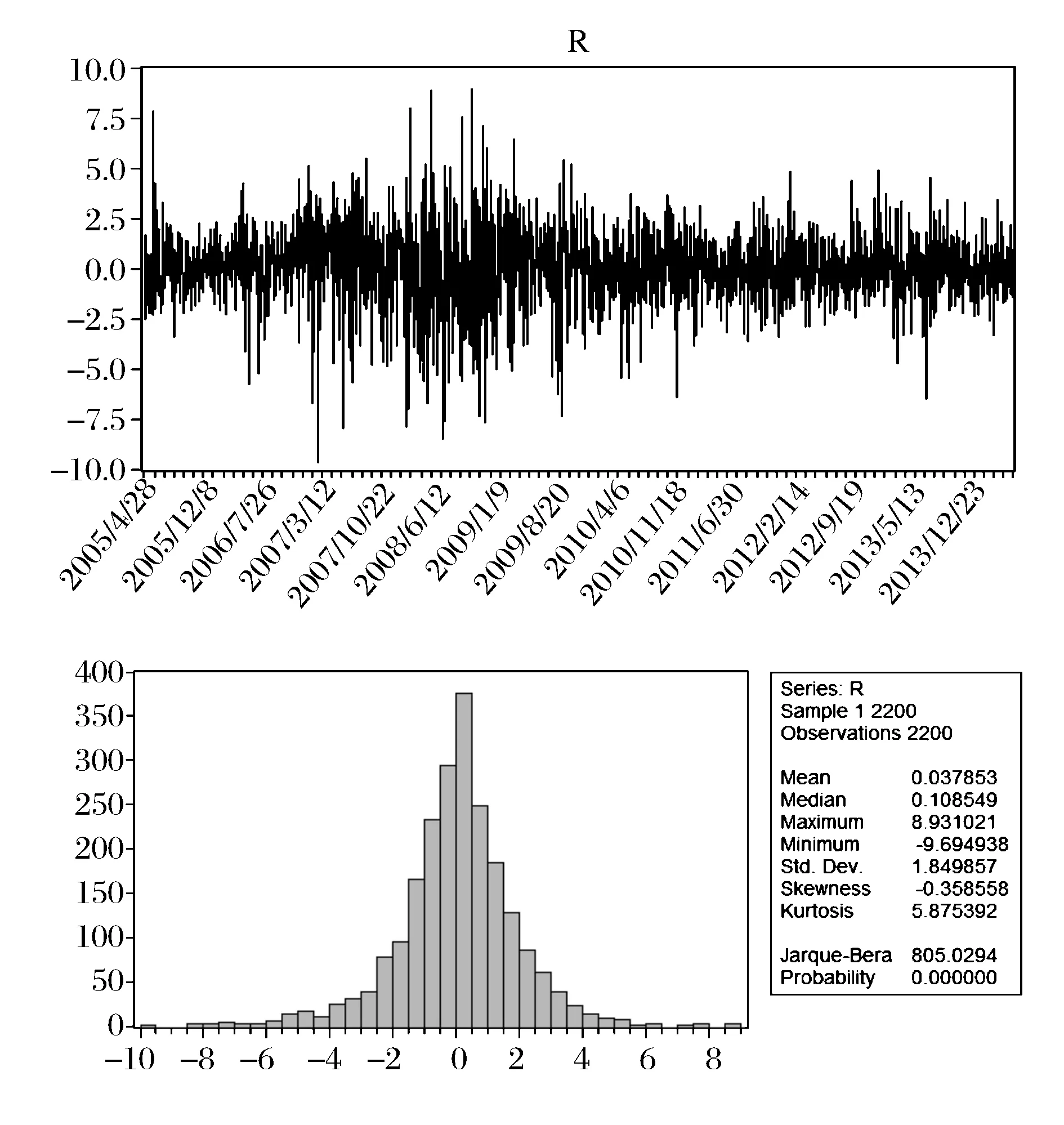
图2 收益率序列的统计特征
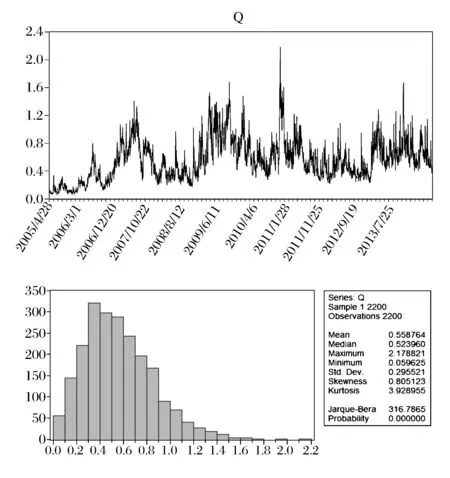
图3 成交量序列的统计特征

变量ADFDF-GLSPPERSKPSS收益率-45.88**-3.13**-45.92**0.042**0.563*成交量-6.18**-2.92**-11.03**1.05**1.15**
注:**和*分别表示在显著水平5%和10%下拒绝原假设。
图2给出了rt序列的基本统计信息,可以看出收益率序列具有左偏厚尾的特征,且不服从正态分布;图3给出了qt序列的基本统计信息,可以看出成交量序列不服从正态分布,具有右偏厚尾的特征。
论文构建的收益率rt对成交量qt的分位数回归模型为:
rt=α(U)+qtβ(U),U|qt~Uniform(0,1)
(13)
其中τα(τ)+qtβ(τ)是τ的连续且严格递增函数。随机变量U取值为τ时,α(τ)+qtβ(τ)便是在成交量为qt的条件下rt的τ分位数。
为避免伪回归,对rt和qt分别用了五种方法进行单位根检验结果如表2所示。根据检验结果可以认为收益率序列和成交量序列都是平稳的,可以直接进行回归分析。
4.1 分位数回归结果
首先利用传统的分位数回归模型进行分析,求出不同分位水平(共取了91个水平)下斜率参数β(τ)的估计以及95%的置信区间,如图4所示,横坐标为分位水平,从0.05到0.95,纵坐标为斜率参数的估计值。图5为不同分位水平下斜率参数显著性检验的值,p值越小说明斜率参数越显著,表3列出了二十一个分位水平下的估计值及统计性质的具体数据。

图4 普通分位数回归的斜率参数估计
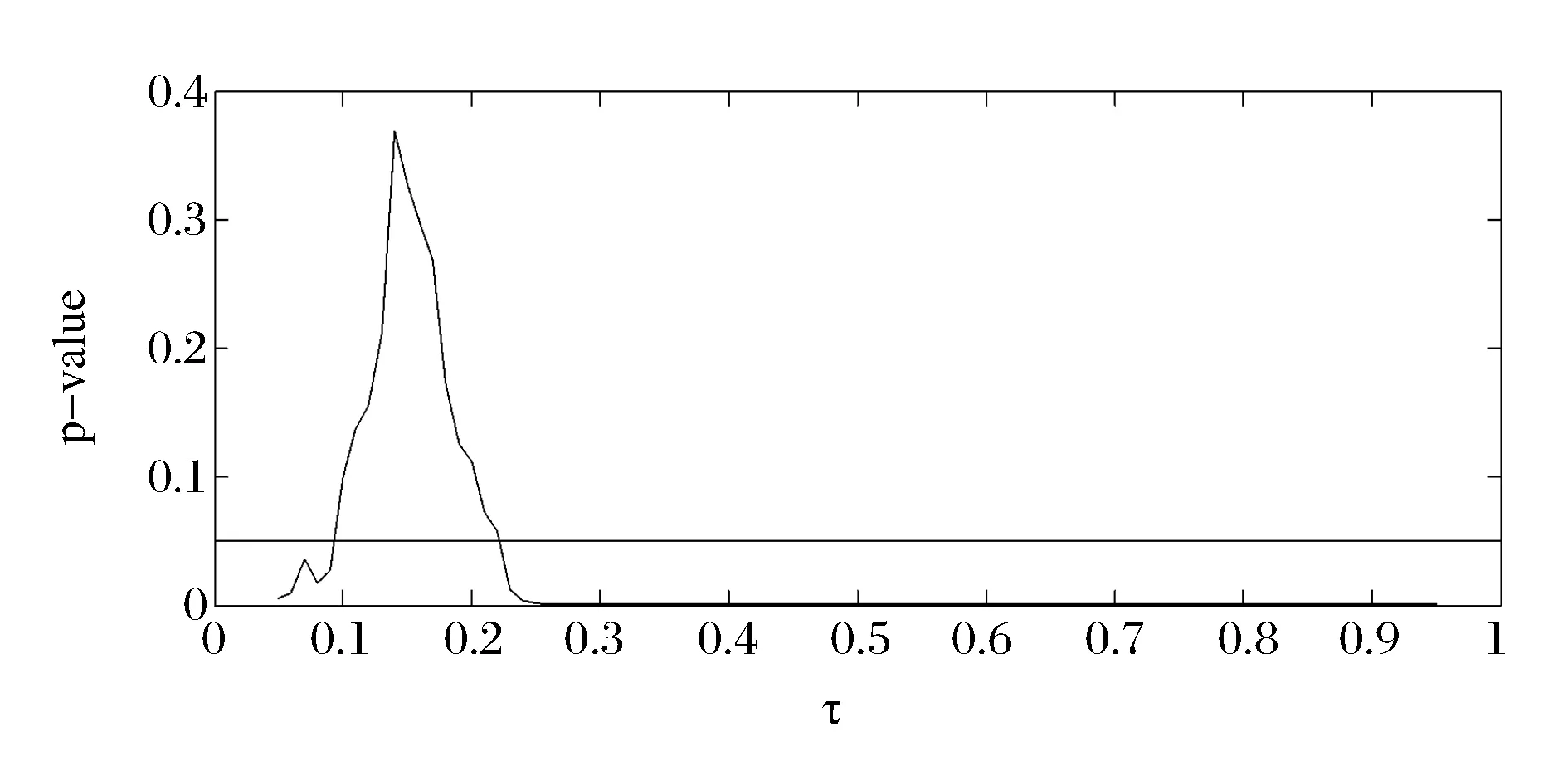
图5 参数估计的p值
由于模型中存在内生性,求得的斜率参数β(τ)并不能客观测度成交量对收益率τ分位点的作用,但可在一定程度上反映成交量与收益率在τ分位点的相关性。从图5可以看出大多数分位水平下系数是显著的,这说明成交量与大多数分位水平下的收益率之间存在相关性。分位水平在区间[0.1,0.2]及附近时,斜率参数并不显著,从图4可以看出分位水平从0.1上升到0.2时成交量与收益率的相关性从负相关转变为正相关。之所以出现这种现象,可能当条件收益率处于较高水平时,投资者的看涨情绪要大于看跌情绪,会继续买入股票,成交量随之增大,而新增资金的入场使得股价继续上扬,这种收益率与成交量的双向影响使得它们之间的相关性为正;而当条件收益率处于较低水平时,股市中的看跌情绪占据主导地位,投资者为减少损失会纷纷抛售手中的股票,成交量虽然增大,但供大于求的市场关系使得股价进一步下跌,于是出现了收益率与成交量呈负相关的现象。
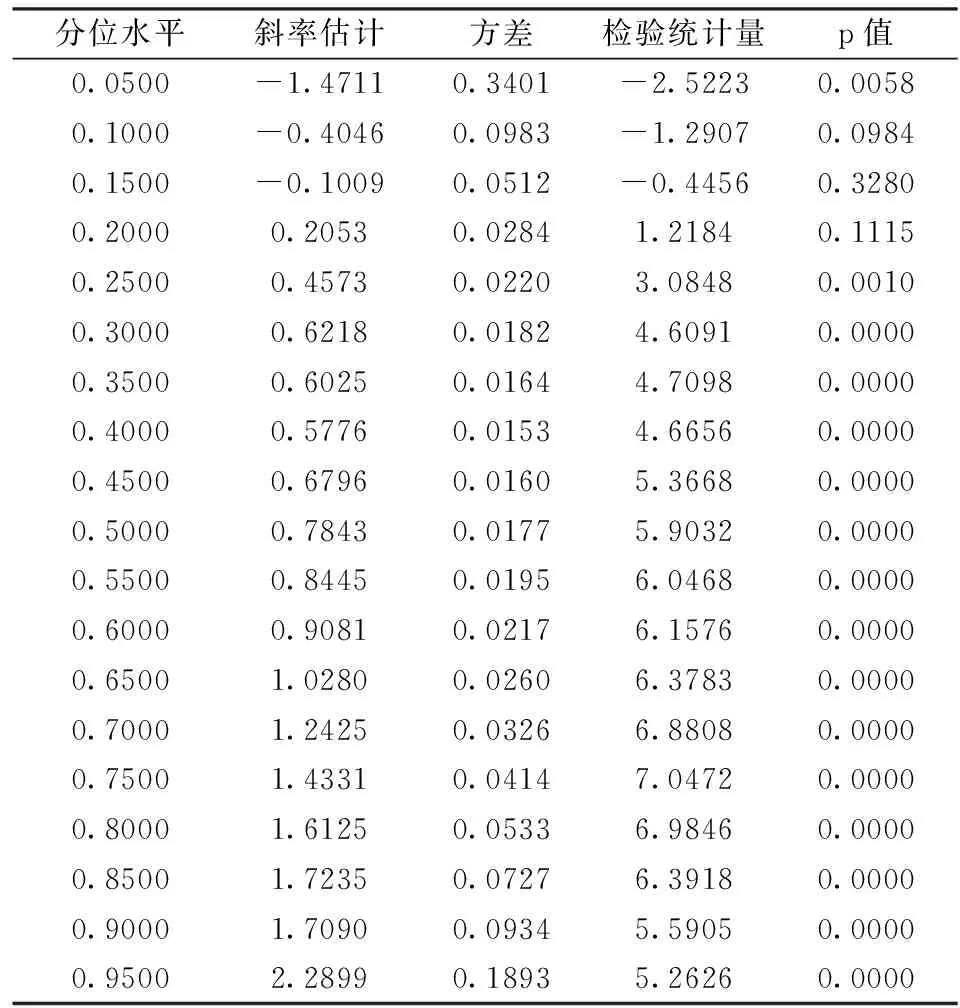
表3 系数估计及显著性检验
从图4还可以看出不同分位水平下得到的参数估计不同,分位水平越高,斜率参数越大。收益率与成交量的相关性为正时,分位水平越大,与成交量的相关性越强,这可能因为条件收益率越高,投资者的看涨情绪越重,对成交量的影响也越大,成交量与收益率的双向影响越明显,相关性也就越强。收益率与成交量的相关性为负时,分位水平越低,与成交量的负相关性越强,这可能因为条件收益率越低,投资者的看跌情绪越重,抛售股票的行为越多,对成交量的影响也越大。0.95分位水平下的收益率与成交量的相关性要大于0.05水平下的收益率与成交量的相关性的绝对值,这说明投资者受乐观情绪的影响要大于受悲观情绪的影响。
4.2 工具变量分位数回归结果
直接用分位数回归方法求出的斜率参数只能在一定程度上反映成交量与收益率不同分位点的相关性,不能够客观度量成交量对收益率的作用,因为斜率参数里也包含了分位水平U对成交量的影响,为了消除这种影响引入前一期的成交量作为工具变量,构建IVQR模型(5),求得的斜率参数估计及置信区间见图6,图7刻画了不同分位水平下求得的p值,p值越小说明系数越显著,可以看出在大多数分位水平下系数都是显著的。二十一个分位水平下的估计值及统计性质的具体数据见表4。
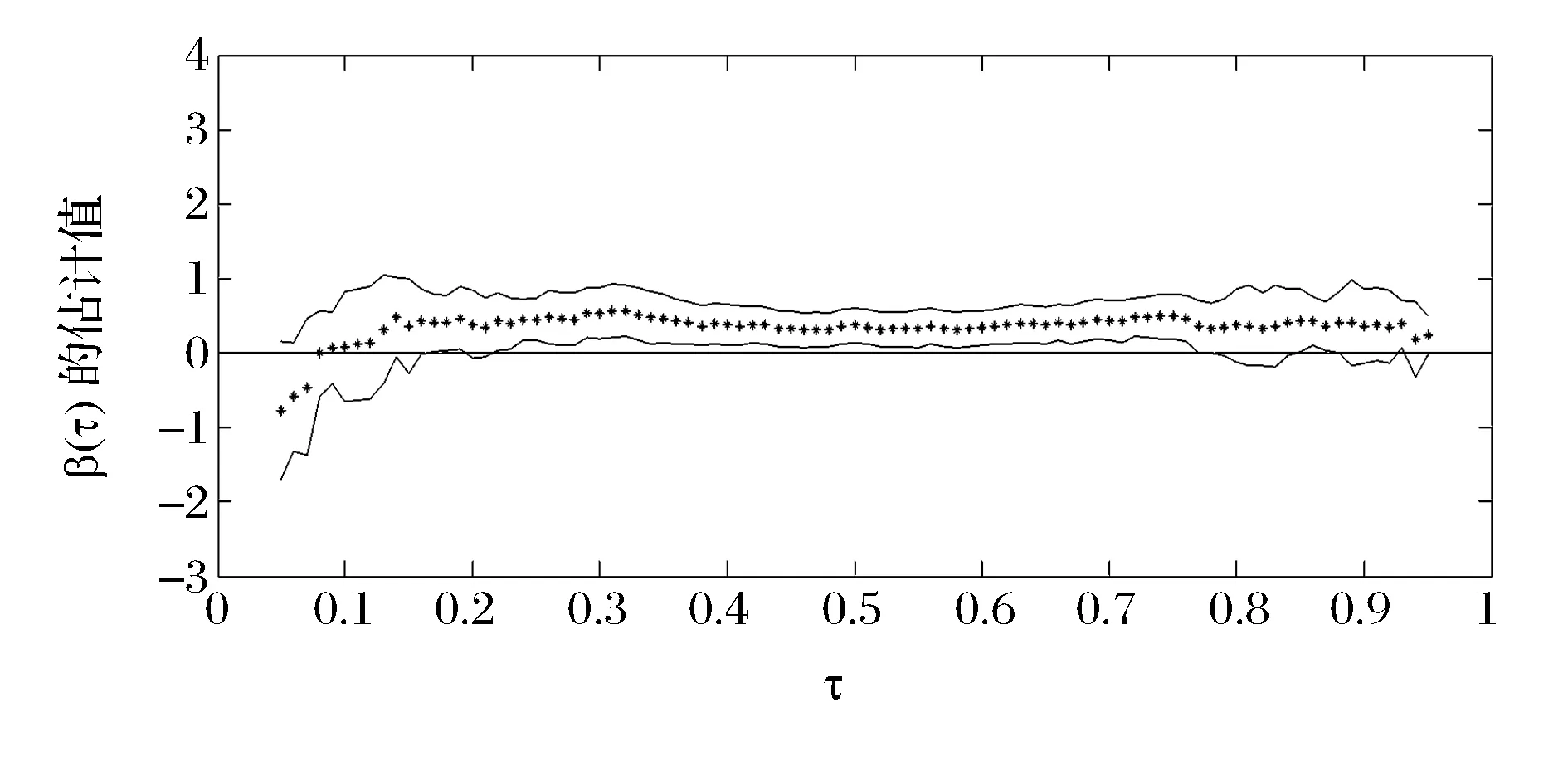
图6 IVQR斜率参数的估计
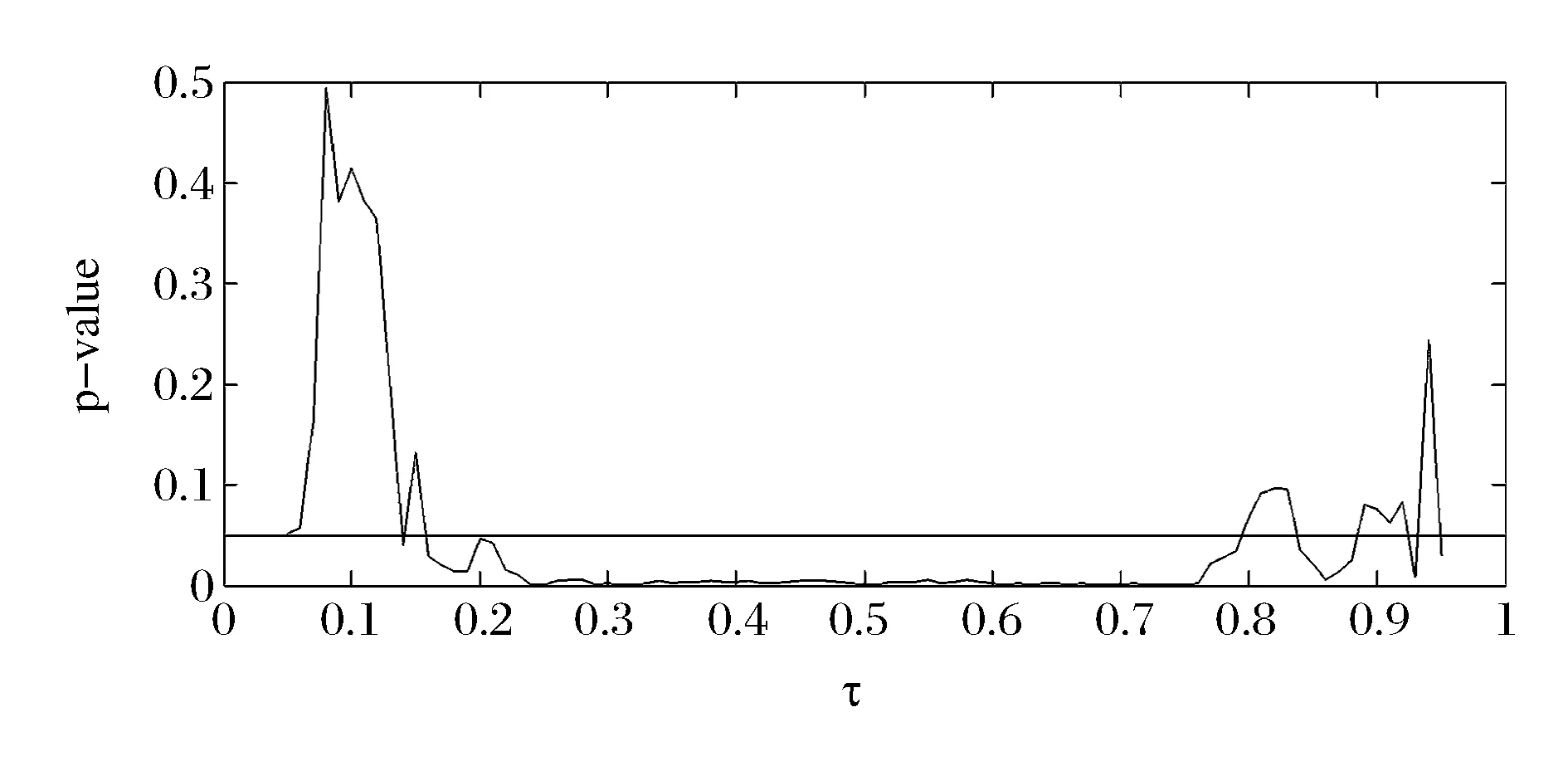
图7 IVQR 参数估计的p值
图6中最左端的斜率参数为负,表明成交量增加反而使得股价降低,这是因为在条件收益率较低时,大部分投资者认为股价会进一步下跌,为减少损失会尽快卖掉手中的股票,此时股市中有大量的股票亟待出售,出现了供大于求的局面,这导致价格进一步下跌。在0.05到0.15的分位水平下,系数由负变正,且在0附近。从表4及图7可看出,在此分位水平下,系数的显著性不明显,当分位水平小于0.05时,系数为负,大于0.15时,系数为正,说明条件收益率处于中段或较高分位水平时,成交量增大会使股价上升,而条件收益率处于较低分位水平时,成交量增大会导致股价下跌。因此在收益率处于相对较低水平时,监管部门可通过一系列政策(如熔断机制)限制成交量,对金融市场进行宏观调控。从0.2分位点到0.8分位点斜率的估计几乎处于同一水平,并不随分位点的增大而增大,这表明在分位水平为0.2到0.8时,成交量增加会推动收益率增加,这种推动效果比较稳定,并不随着收益水平的增加而有明显的改变。在条件收益率处于较高水平时增加成交量对收益率继续上扬的推动作用与收益率处于正常水平时成交量的推动效果并没有明显的差异;而且从表中可以看出在收益率处于非常高的分位水平(0.8以上)时,系数的显著性水平并不高,这表明条件收益率处于高分位水平时,增加成交量可能不会使收益率继续上扬。因此在条件收益率处于相对较高水平时,交易量的增加并不会带来收益率的持续增加,投资者在做投资决策时,应保持理性,综合考虑多种因素后谨慎投资。
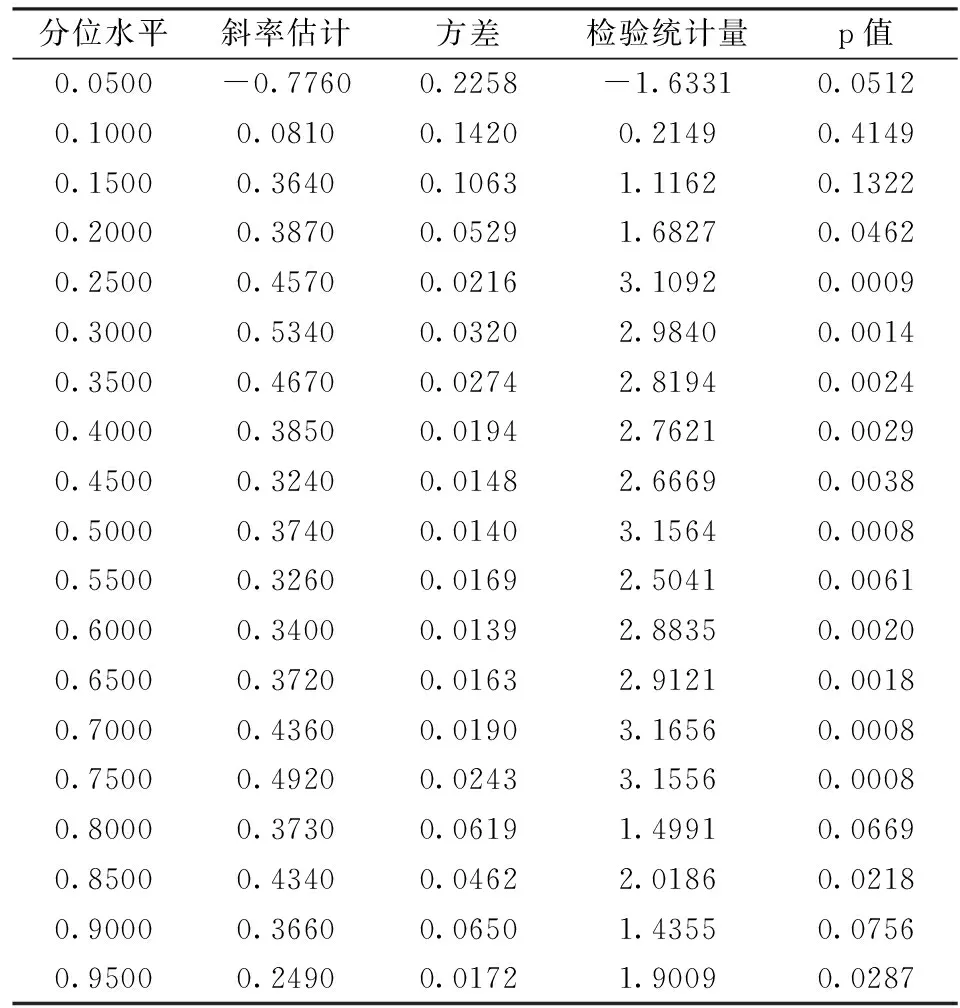
表4 IVQR系数数估计及显著性检验
4.3 两种方法结果的比较
本节将分位数回归方法和引入工具变量后的IVQR方法求出的结果放在同一张图中进行比较(见图8)。图中实线代表直接用分位数回归方法求得的斜率参数估计,星线代表加入工具变量后求得的斜率参数估计。
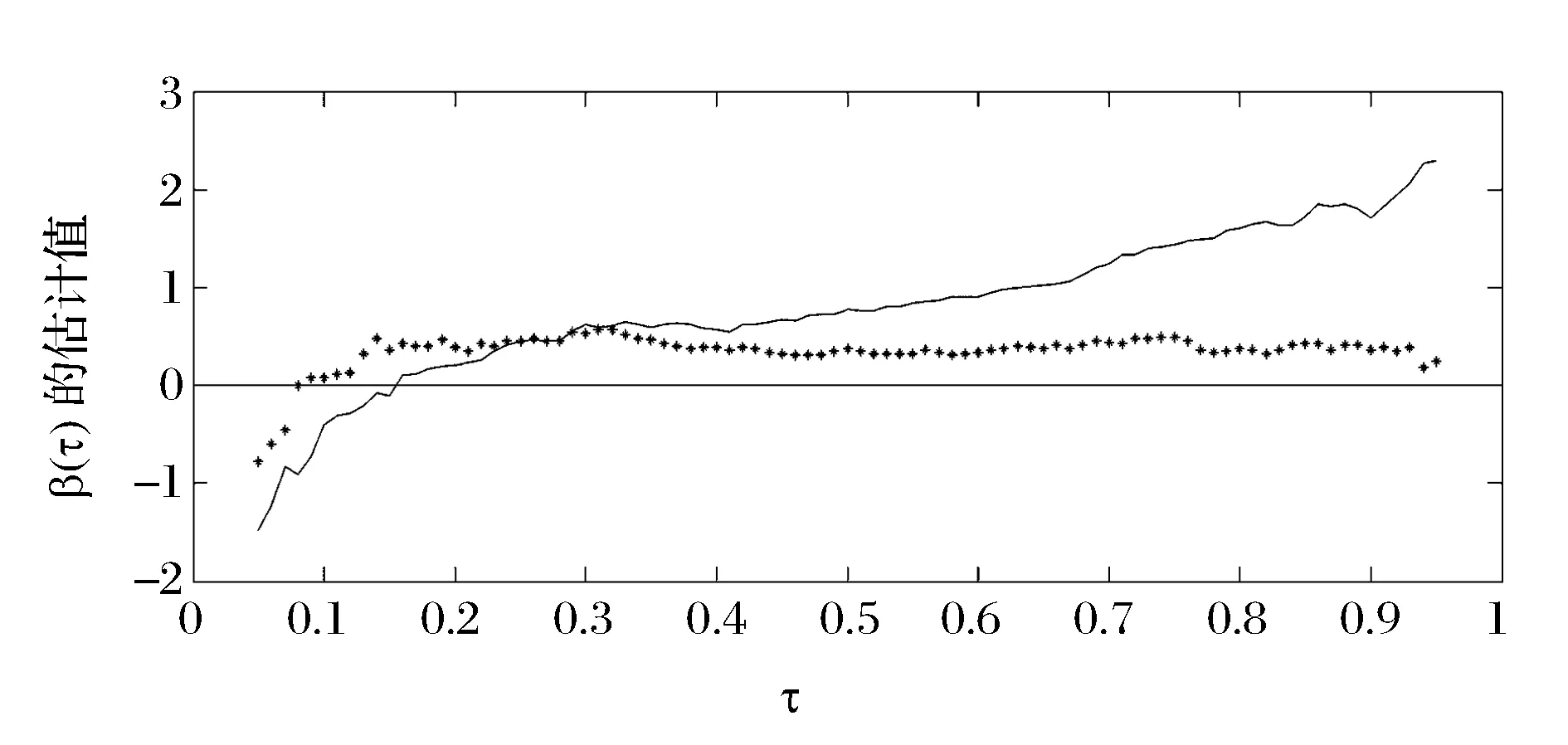
图8 两种方法估计的斜率参数对比
直接用分位数回归方法求出的结果,只能反映成交量与不同分位水平下的收益率的相关性,加入工具变量后求出的估计,考虑了收益率分位水平对成交量的影响,可以较为准确的反映不同分位水平下成交量对收益率的影响。由图8可以看出星线要比实线平缓,实线的走向表明在τ∈[0.2,0.9]时相关性随分位水平增大而增大,星线在τ∈[0.15,0.8]范围内接近于一条水平的直线,表明成交量对0.15到0.8分位水平下的收益率影响差别不大。星线与实线的差异体现出加入工具变量的作用,直接用分位数回归方法求出的斜率中还包含有分位水平对成交量的影响,导致估计结果出现较大的偏差,并不能准确地度量成交量对不同分位水平的收益率的作用,只能在一定程度上反映两者的相关程度,而IVQR模型考虑到了这种影响,通过引入工具变量规避这种影响,更加客观地度量成交量对收益率的影响。
5 结语
论文首先通过蒙特卡洛模拟方法论证了IVQR估计比QR估计具有更小的偏差以及更强的稳健性。接着利用分位数回归方法对股市成交量与不同分位水平下收益率的相关性进行了研究,结果表明在条件收益率处于中段或较高的分位水平时,收益率与成交量成正相关,且相关性随着条件收益率的增大而增大;条件收益率处于较低的分位水平时,收益率与成交量成负相关,且条件收益率越低相关性越强;成交量与收益率0.95分位点处的相关性要大于0.05分位点处的相关性的绝对值,这反映了中国股民比较乐观,看涨情绪对投资者的影响要比看跌情绪的影响大。
因为收益率的分位水平对成交量有一定的影响,传统的分位数回归模型估计的斜率并不能客观衡量成交量对收益率的作用,它还包含分位水平的部分影响,因此论文进一步选取前一期的成交量作为工具变量,构建IVQR模型进行分析。与传统方法结果相比,IVQR模型得到的斜率在大多数分位水平下都是显著的,表明成交量对大多数分位水平下的收益率有影响。条件收益率处于中段或较高的分位水平时,成交量的增加会使股价上升,而条件收益率处于较低的分位水平时,成交量的增大会导致股价下跌。另外本文还发现,在分位水平为0.15到0.8时(即非极端的情况),成交量与收益率的相关性虽然在增大,但成交量对收益率的影响基本不变;当分位水平非常高(0.8以上)时,增加成交量可能不会使收益率继续上扬。
研究结果还表明应用分位数回归模型分析问题过程中,如果模型中被解释变量受分位数的影响,即出现内生性问题,比较有效的处理方法是利用工具变量的分位数回归模型。相较于一般分位数回归模型的分析结果,工具变量分位数回归解决了分位数回归模型中可能存在的内生性问题,模拟结果表明工具变量分位数回归具有较小的偏差和均方误差,参数估计更加靠近真实值,这样使得经济分析结果更加真实可靠。中国金融市场的发展具有较大的异质性,工具变量分位数回归能够结合金融发展的具体现象,针对变量的不同阶段和特点进行研究。本文的研究方法对于宏观经济现象的分析具有重要的指导意义,能够为政府决策部门提供科学、客观的依据,从而促进经济市场平稳运行。
[1] Crouch R L.The volume of transactions and price changes on the New York stock exchange[J].Financial Analysis Journal,1970,26(4):104-109.
[2] Karpoff,Jonathan M.The relation between price changes and trading volume:A survey[J].Journal of Financial and Quantitative analysis,1987,22(1):109-126.
[3] Lamoureux C G,Lastrapes W D.Heteroskedasticity in stock return date:Volume versus GARCH effects[J].Journal of Finance,1990,45(1):221-229.
[4] Chen Gongmeng.The dynamic relation between stock returns trading volume and volatility[J].The Financial Review,2001,36(3):153-174.
[5] 郭梁,周炜星. 基于高频数据的中国股市量价关系研究[J].管理学报,2010,7(8):1242-1247
[6] 吴冲锋,王承炜,吴文锋.交易量和交易量驱动的股价动力学分析方法[J].管理科学学报,2002,5(1):1-11.
[7] 吴秋芳,王长辉,唐亚勇.基于GARCH类模型和BP神经网络的量价关系实证研究[J].四川大学学报,2013,50(4):703-708
[8] 卢英,刘晓艳.经济转型时期股指收益率与成交量关系分析[J].统计与决策,2015,(8):170-172.
[9] 陈怡玲,宋逢明.中国股市价格变动与交易量关系的实证研究[J].管理科学学报,2002,3(2):62-68.
[10] 田大伟,金泰一.中国股票市场量价关系的重新审视——基于鲁棒(Robust)方法的研究[J].中国管理科学,2004,12(S1): 279-283.
[11] 翟爱梅,周彤.基于市场参与者行为假设的股票市场量价关系研究[J].中国管理科学,2011,19(4):31-37.
[12] 翟爱梅,王雪峰.基于弹塑性理论构建的股票量价关系模型[J].统计与决策,2010,(3):144-146.
[13] 徐加根,孙文佳,牛锋.我国A股市场交易量信号的差异性研究[J].财经问题研究,2015,(7):52-57.
[14] 林德钦.上海股市收益率与成交量的动态关系研究——基于分位数回归模型的分析[J].金融教学与研究,2014,157(5): 48-52.
[15] Chernozhukov V, Hansen C. Instrumental variable quantile regression: A robust inference approach [J]. Journal of Econometrics, 2008, 142(1):379-398.
[16] Koenker R,Bassett G W. Regression quantiles [J].Econometrica,1978,46(1):33-50.
[17] Koenker R. Quantile regression[M].Cambridge:Cambridge University Press,2005.
[18] Koenker R, Machado J A F.Goodness of fit and related inference processes for quantile regression [J].Journal of the American Statistical Association, 1999, 94(448):1296-1310.
[19] Durrett R. Probability:Theory and examples[M]. Belmont, CA: Duxbury Press,Second Edition,1996.
[20] Chernozhukov V, Hansen C.Instrumental quantile regression inference for structural and treatment effect models[J].Journal of Econometrics, 2006,132(2): 491-525.
Analysis of Yield and Volume in China’s Stock Market—Based on IVQR Models
REN Yan-yan, Li Shao-min
(Academy of economics,Shandong University, Jinan 250100,China)
Based on quantile regression models, the correlation between volumeand yield on different levels is studied.In order to eliminate the influence of yield’s level to the volume, an instrumental variable and instructa IVQR model are introduced, based on which the effect of volume on yield of different levels can be analyzed objectively.Monte Carlo simulation shows that IVQR estimator has less bias and stronger robustness.In empirical analysis,it is found that yield and volume are positively correlated if the yield is on a high level, the higher the level is,the larger the correlation will be;and that yield and volume arenegativelycorrelated if the yield is on a low level, the lower the level is,the larger the correlation will be.We also find that the volume’s effects on yields of most levels are similar.The outcome simultaneously shows that IVQR can dispose the endogeneity in models.
yield; volume; quantile regression models; IVQR Models
1003-207(2017)08-0011-08
10.16381/j.cnki.issn1003-207x.2017.08.002
2016-04-29;
2017-03-17
国家社会科学基金资助项目(12BTJ015);山东省自然科学基金资助项目(ZR2014AM014)
李劭珉(1991-),男(汉族),山东兖州人,山东大学经济学院,博士生,研究方向:计量经济学,E-mail:lsmjim@163.com.
F224.0
A
