基于纹理特征的自适应插值
2017-09-15张云峰姚勋祥包芳勋张彩明
张云峰 姚勋祥 包芳勋 张彩明
1(山东财经大学计算机科学与技术学院 济南 250014)2(山东大学数学学院 济南 250100)3 (山东大学计算机科学与技术学院 济南 250100)
基于纹理特征的自适应插值
张云峰1姚勋祥1包芳勋2张彩明3
1(山东财经大学计算机科学与技术学院 济南 250014)2(山东大学数学学院 济南 250100)3(山东大学计算机科学与技术学院 济南 250100)
(yfzhang@sdufe.edu.cn)
在传统有理插值函数的基础上构造出一种新的混合插值模型.该混合插值模型是有理函数与分形插值函数的有机整体,可由形状参数和尺度因子唯一确定.由于分形是刻画图像复杂度的有效工具,引入分形维数描述纹理的复杂程度.首先,提出一种基于局部分形维数的自适应阈值选取的方法,将整幅图像划分为纹理区域和非纹理区域.在纹理区域采用有理分形函数插值,在非纹理区域采用有理函数插值.尤其在有理分形插值模型中,提出一种基于分形维数的精确计算尺度因子的方法.最后,通过优化形状参数进一步提高插值图像质量.实验结果表明:提出的基于图像特征的混合插值模型与当前经典算法相比,尤其是在处理纹理图像方面,具有明显优势.
混合插值;局部分形维数;自适应阈值;参数优化;有理分形
图像插值,或称图像放大,是指由低分辨率图像获取高分辨率的图像,在本质上是通过已知像素估算出未知像素.图像插值技术能够在一定条件下保持丰富的纹理信息和锐利的边缘.图像插值技术在图像处理领域起着重要的作用并且广泛应用于各个领域,如航空航天、军事、通信、遥感卫星、电视及电影制作等.诸多插值算法被广泛地用于现实中,如最近邻、双线性、双三次以及样条插值[1-2]等.虽然这些传统的插值算法比较有效,但是往往会产生边界模糊、走样等.
为了弥补传统插值算法的不足,许多经典的插值算法被提出.文献[3]首先从低分辨率图像估计局部协方差系数,然后在高分辨率图像中基于低分辨率和高分辨率协方差的几何对偶性,利用估计出的协方差做自适应插值.这种基于协方差的插值方法具有较高的运算复杂度.在文献[4]中,Hiroyuki等人提出泛化的核退化自适应插值算法,将非参数统计方法与核退化方法结合,提出泛化的方法用于图像处理和重建.核退化的方法可以有效减少估计误差,但这种方法往往也会产生边界模糊和纹理错乱现象.在文献[5]中,Zhang等人提出基于线性均方差的图像插值方法.对于每一个被插像素点,将其邻域划分为2个观测子集,并从正交的2个方向估计缺失的像素.Zhang等人在文献[6]中提出一种软决策的插值技术,这种方法不是一次估计一个像素而是一次估计一组像素.此方法使用二维分段自回归模型,能够学习和适应不同结构.这种算法能很好地保持插值图像的空间相关性,且具有良好的主观视觉质量和图像质量客观评价值.以上2种方法均是采用非连续函数,这种方法常常产生斑点噪声以及边界错乱.Dong等人[7]将非局部自回归模型与稀疏表示相结合.传统的稀疏表示未能包含丢失像素的结构信息导致其效果不理想,非局部自回归模型可以有效降低样本矩阵与稀疏表示字典的相关性,从而使得稀疏表示更加有效.虽然这种方法取得了较好的视觉效果,但是其算法时间复杂度较高.
近几年,Jeong 等人[8]提出了一种基于局部方向自相似性的多帧图像超分辨率算法.窦诺等人[9]提出一种基于图像块在训练字典下稀疏表示的协同处理方法,用来解决含噪图像超分辨的问题.在文献[10]中,曹世翔等人提出一种映速有效的边缘特征点提取方法,实现多分辨率图像融合.Jha 等人[11]提出了一种新的图像插值方法,该方法利用逆梯度和像素间的距离自适应获取权值,以此估计未知像素.在文献[12]中,Zhu等人提出一种基于非局部几何自相似的插值算法,基于图像块梯度方向变化以及相似块极小化获取理想权重系数.在文献[13]中,Zhang等人提出结合结构信息和稀疏表示的方法以提高基于稀疏表示方法的超分辨效果.然而以上方法在复杂纹理图像的处理中效果并不理想,会产生纹理错乱等现象.
如今,与理想核函数接近的有理函数作为一种新的方法用于图像插值中.总的来说,采用有理函数重构出的图像具有较好的视觉效果,无块状痕迹,模糊程度较低等.在文献[14]中,Hu等人提出自适应切触有理插值函数以保持边界,这种函数是对理想核函数更精确的逼近.在文献[15]中,Carrato 等人提出一种新的基于现实图像合成的内插算法.有理算子提供边缘敏感数据插值,以此减少人工痕迹的出现. 在文献[16]中,Liu等人构建出基于权重的自适应插值函数,包含边界信息的权重系数可由距离、梯度、采样点的差商自适应计算得出.然而,有理函数在纹理细节保持等方面效果并不理想.由于分形是描述纹理的有效工具,基于分形分析的纹理描述子广泛应用于纹理分割和分类[17-21].Xu等人[22]提出一种基于局部分形分析的单幅图像超分辨增强算法.在文献[23]中,将分形编码看作是特征的相似性评价标准,通过搜索内部图像块和使用的低分辨率单一图像的图像相似融合重建高分辨率图像信息块,实现基于分形编码的图像超分辨率增强.在文献[24]中,Zhai提出一种新的基于分形的PLC OFDM信号重建方法.由此,提出一种既可以保持纹理细节又能保持锐利边界的算法是必要的.
为了解决上述问题,在先前有理函数[25-27]的研究基础上,本文提出一种有理分形的混合插值模型.该模型将形状参数包含于分形函数中,通过尺度因子和形状参数可确定唯一的插值模型.给定不同的尺度因子的值,模型的表达形式随之变化.根据图像的特征信息,将图像划分为不同区域.区域划分是依据分形特征的自适应阈值选取.对于不同的区域,我们采用不同的插值函数.最后,通过对表达式中参数的优化,进一步提高图像的插值质量.本文算法的流程图如图1所示:
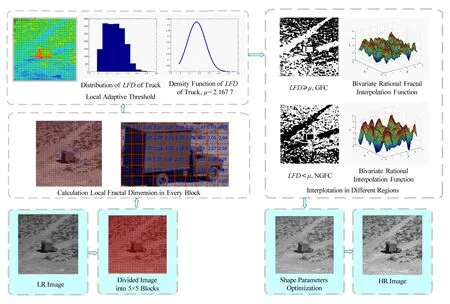
Fig. 1 Flowchart of mixing interpolation system图1 混合插值系统算法流程图
1 有理分形插值函数构造
有理分形插值函数是本文混合插值算法的基础.在介绍经典双变量插值函数的基础上,本节提出的一种新的双变量有理分形插值函数.
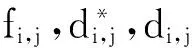
(1)
其中,0≤λ≤1,令φm(y):J→Jm为线性压缩同胚,并且满足:
(2)
其中,0≤μ<1,
(3)
且
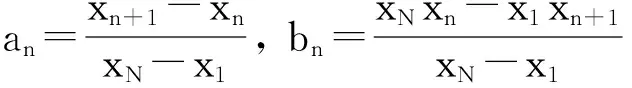
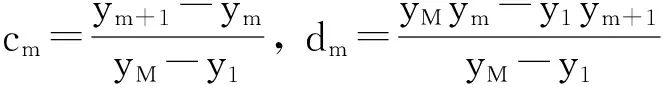
令hi=xi+1-xi,lj=yj+1-yj,θ=(x-xi)hi,η=(y-yj)lj.对每一个数y=yj,j=1,2,…,M构造x方向的插值函数如下:
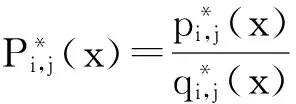
(4)
其中,
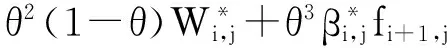
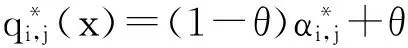
且
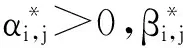
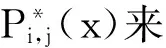
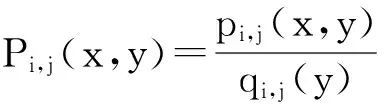
(5)
其中,
其中,
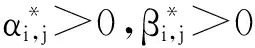
由此构造迭代函数系(IFS)
{I×J×R;(φi(x),φj(y),Fi,j(x,y,z))}.
(6)
记HN=xN-x1,LM=yM-y1,对[x1,xN;y1,yM],θ=(x-x1)(xN-x1),η=(y-y1)(yM-y1),Bi,j(x,y)表达式如下:
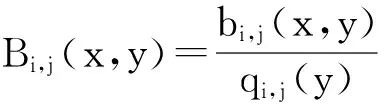
(7)
其中,
且
其中,
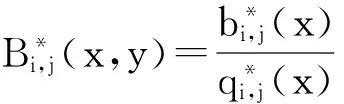
(8)
且
其中,
且θ=(x-x1)(xN-x1),η=(y-y1)(yM-y1),Bi,j(x,y)满足:Bi,j(x1,yM)=f1,1,Bi,j(xN,y1)=fN,1,Bi,j(x1,yM)=f1,M,Bi,j(xN,yM)=fN,M,Fi,j(x,y,z)=si,jz+Pi,j(φi(x),φj(y))-si,jBi,j(x,y),其中si,j为迭代函数系的尺度因子且|si,j|<1.
因此,上述定义的迭代函数系统存在唯一的吸引子G,且为连续函数记为ψ(x,y).式(6)中定义的有理分形插值函数(fractal interpolation function, FIF)称之为双变量有理分形插值函数(bivariate rational fractal interpolation function, BRFIF),其表达式如下:
ψ(φi(x),φj(y))=si,jψ(x,y)+
P(φi(x),φj(y))-si,jBi,j(x,y).
(9)
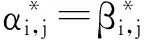
2 插值算法
在本节我们将讨论如何利用上述构造的模型由低分辨图像获取高分辨图像:1)计算图像的分形维数,以此作为划分纹理区域与非纹理区域的依据;2)根据图像局部特征,不同区域采用不同插值模型,在纹理区域采用有理分形插值函数,在非纹理区域采用有理函数插值;3)根据局部分形维数与全局分形维数的关系准确计算尺度因子;4)通过参数优化技术进一步提高图像的插值质量.
2.1 基于分形维数的区域划分
对于同时包含纹理区域和非纹理区域的复杂图像,区域划分是插值算法的关键步骤,区域划分的精确与否将直接影响图像的插值质量.在本文中,我们利用分形维数描述图像的复杂性,并以此将图像划分为纹理区域和非纹理区域.阈值选取是区域划分的关键,因此阈值选取的精确与否会直接影响区域的划分.
2.1.1 分形维数
分形维数也被称作全局分形维数,是分形理论中的重要内容.由于分形维数与人眼区分纹理粗糙度相一致,分形维数被视为描述纹理复杂性的有效工具.全局分形维数用来描述整幅图像的复杂程度,而局部分形维数(local fractal dimension,LFD)用来描述图像局部小块的复杂性.“毯子覆盖法”是一种被广泛应用的计算分形维数的方法,其优势在于可以覆盖分形维数的取值范围.接下来将介绍如何利用毯子覆盖法计算全局分形维数和局部分形维数[28].图像灰度曲面可看作灰度函数H(i,j),毯子的上下表面分别记作Tε,Bε.初始时,T0(i,j)=B0(i,j)=H(i,j).当ε=1,2,…,N,毯子的上下表面可定义为
(10)其中d(i,j;m,n)代表(i,j)与(m,n)两点之间的距离,应用图像处理中的膨胀和腐蚀技术,选择尺寸大小为ε的结构元素,则不同尺度对应的表面积测度A(ε)为
(11)
其中,T为膨胀层面积,B为腐蚀层面积.此时图像的表面积测度可记作:
A(ε)=kε2-D,
(12)其中A(ε)是尺度ε下的表面积.应用最小二乘法对双lg-lg曲线拟合,可以计算出分形维数的数值如下:
D=2-k.
(13)
2.1.2 局部自适应阈值

Fig. 2 Regional division by different methods图2 不同方法区域划分对比
纹理区域最主要的特征是其灰度值变化剧烈,一个简单的区分纹理的方法就是阈值选取.区域划分的关键在于精确选择阈值,因为阈值选取的正确与否将直接影响插值函数的选取,从而影响插值质量.如果阈值较小,会错把非纹理区域视为纹理区域;相反,如果阈值较大,那么纹理区域将会被错误地认作是非纹理区域.
自动阈值选取是一种广泛应用的方法,它根据公式利用图像特征信息自适应计算阈值大小.自动阈值[29]计算为
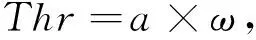
(14)
其中,a=[3,5],x代表每个像素点的灰度值,n为像素点数.整幅图像灰度值均值如下:

(15)
其中,a=5,x代表每个像素点的灰度值,median是指整幅图像灰度中值.这种阈值选取的方法忽略了图像自身的结构信息,同时单纯依靠全局灰度值阈值选取的方法是不精确的.因此,我们提出一种可以描述纹理复杂性的基于分形维数的阈值选取方法.经过大量实验,我们发现自然图像局部分形维数的分布近似符合正态分布.正态分布,又称高斯分布,是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力.若随机变量x服从一个数学期望为μ、标准方差为σ2的高斯分布记为X~N(μ,σ2),则其概率密度函数为
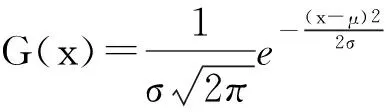
(16)
高斯模型广泛应用于图像处理领域,利用高斯概率密度函数作为量化标准将整体分为部分通常是准确的.图像纹理区域高斯模型的建立原理与过程:局部分形维数的直方图反映图像分形维数出现的次数,同样也可以认为是其密度分布.如果纹理区域和非纹理区域存在差别,其局部分形维数直方图会呈现出“铃形”曲线形状.因此整幅图像就可以分为2部分:
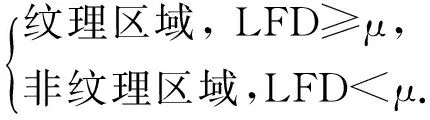
(17)
利用“毯子覆盖法”计算每一个5×5子块的分形维数.按照式(16),μ为局部分形维数的均值,即为选取的划分纹理区域与非纹理区域的阈值.在本文的插值算法中,通过计算每一子块的分形维数,如果其值大于μ,被认为是纹理区域,否则为非纹理区域.图2为自动阈值方法和本文阈值选取方法的对比效果图.图3是包含纹理与非纹理区域的实验图像.局部分形维数的范围为2.0~3.0.为了证明此方法的有效性,图4是其对应的概率密度函数,图5为通过阈值二值化测试图像的结果.

Fig. 3 Images used for discriminating textures图3 区分纹理区域实验图
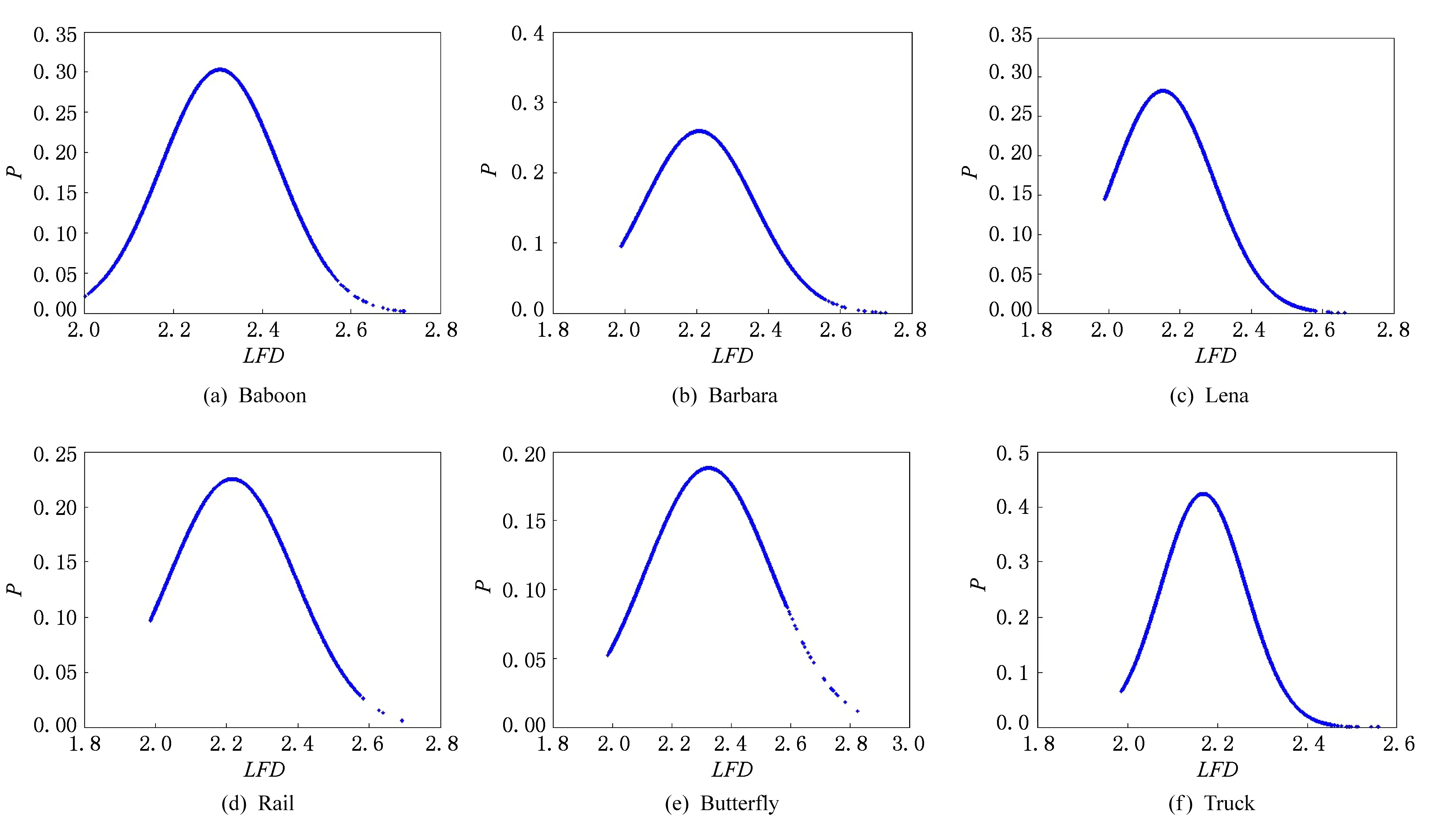
Fig. 4 Density function of LFD of images图4 局部分形维数密度函数

Fig. 5 Results of edge detection图5 边界检测结果图
2.2 自适应插值算法
本文的插值模型为混合插值模型,利用其表达式的多样性分别对纹理区域和非纹理区域处理.根据子块的区域特征,其形状参数可以做调整以更符合图像的结构特征.通过以上步骤,整幅图像被分成纹理区域与非纹理区域.在非纹理区域,插值函数为双变量有理插值;在纹理区域,插值函数为有理分形插值.
2.2.1 纹理区域插值
对于纹理区域,其插值模型表达形式如下:
ψ(φi(x),φj(y))=si,jψ(x,y)+
P(φi(x),φj(y))-si,jBi,j(x,y),
(18)
其中α,β为待优化的形状参数.本文2.4节将讨论形状参数的优化,除此之外,公式中还包含尺度因子si,j的待确定参数.
2.2.2 非纹理区域插值
对于非纹理区域,其插值函数的表达式为
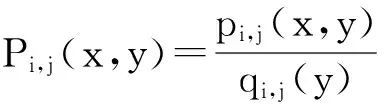
(19)
其中,
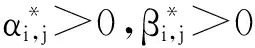
2.3 基于分形维数的尺度因子计算
显然,随机选取尺度因子对图像插值来说是不精确的.针对现实情况,通过已知信息准确计算尺度因子具有重要实践意义.随着尺度因子精确性的提高,本文的插值函数就更接近理想核函数.一般来说,尺度因子通常作为自由参数,或者给出其变化范围[30-31].由于分形维数与尺度因子密切相关,本文中通过分形维数精确计算尺度因子,其表达式如下:
(20)
其中,FD是全局分形维数,N为平面的拓扑维数,N=2.考虑到尺度因子si,j对插值函数的影响,我们控制其他形状参数不变.如图6所示,插值曲面形状受尺度因子影响较大.尺度因子的变化越小(si,j→0),构造的插值函数变化也越小.针对图像,图7给出PSNR随着尺度因子变化情况,当尺度因子在[0,0.3]变化时,峰值信噪比(PSNR)取得最大值.因此,精确计算尺度因子可以有效提高插值质量.实验也刚好证明了我们方法的正确性.
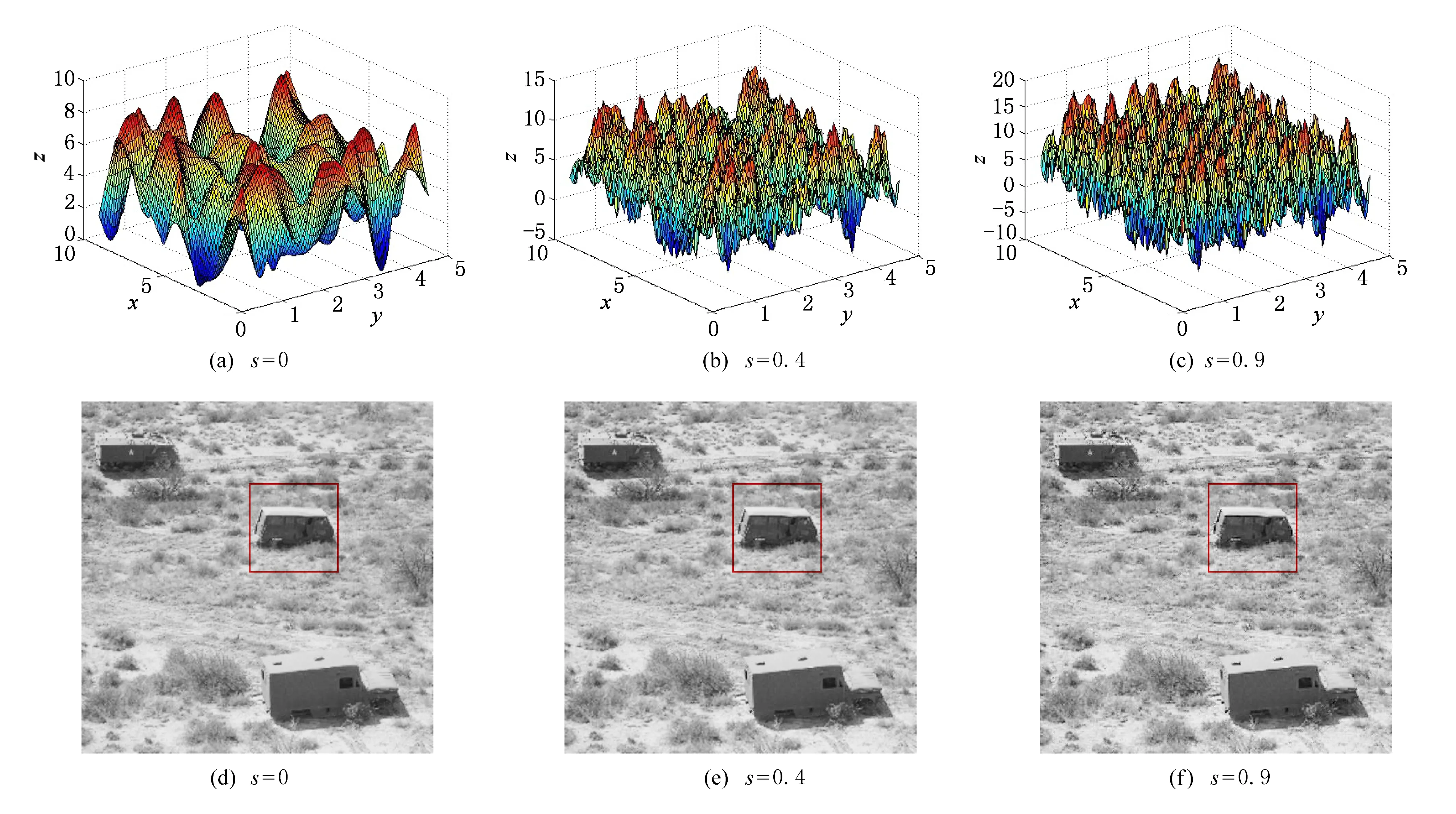
Fig. 6 Comparison of interpolation with different scaling factor图6 不同尺度因子下插值曲面和图像对比
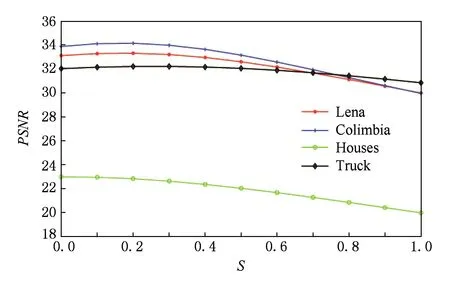
Fig. 7 PSNR changes with scaling factor图7 PSNR随尺度因子变化
2.4 形状参数优化
文献中常用的一种简单的刻画插值的精确性方法是比较插值图像与原图之间的差异.主要是通过计算峰值信噪比(PSNR),其定义如下:
(21)
其中,MSE是原图像与插值图像之间的均方误差, 为图像中灰度的最大值,8位图像的最大值为255.将含有α,β的式(19)带入到式(21)中,记为U(α,β).通过极小化U(α,β) 可以获得局部最优的α,β值,表达式如下:
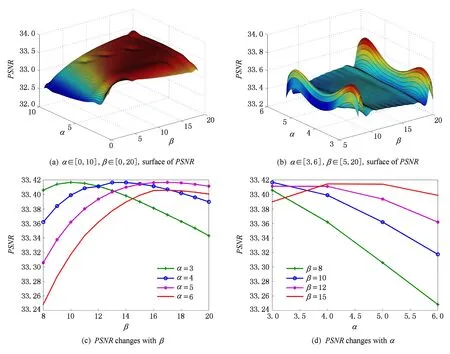
Fig. 8 PSNR changes with shape parameters图8 PSNR随形状参数变化情况
(22)
很显然,采用此种方法获取最优化形状参数具有较高的时间复杂度.下面给出数值化优化参数的算法步骤.
算法1. 参数优化算法.
输入:参数取值范围;
输出:PSNR取最大值时参数取值.
① 对于参数取值范围{(α,β)|0≤α≤10,0≤β≤20}, 分别计算每一对(α,β)的PSNR值;
② 假定PSNR>T为目标值,选取此时(α,β)的取值范围;
③ 固定α的值,选取此时PSNR最大时β的取值;
④ 固定β的值,选取此时PSNR最大时α的取值;
⑤ 获取参数的最优化值.
对于给定的插值函数,插值质量可以通过调节参数进一步提高,本文是以PSNR作为目标函数,从而获得最优的参数取值.
如图8(a)所示,PSNR随着参数变化而发生变化.当α∈[4,5],β∈[14,16] 时,PSNR取得最大值.在图8(c)中,当α取定值、β∈[13,15]时,PSNR达到峰值;当β取定值、α∈[3,5] 时,PSNR达到峰值.其交集即为α,β的最优取值.
3 实验结果与分析
如第2节所述,通过分形特征分析,区分出图像的纹理区域和非纹理区域.纹理区域和非纹理区域可以选择同一个插值模型的不同参数来处理.在纹理区域,需要对参数自适应优化处理,进一步提高插值图像质量.
我们选取了7幅图像作为测试图像,如图9所示.测试图像的尺寸均为512×512.比较算法均为近年经常被引用的且多次比较过的算法:NEDI[3], DFDF[5],SAI[6],NARM[7].

Fig. 9 Images used for quantitative comparison图9 对比实验图像
我们把高分辨率图像下采样获得低分辨率图像,采样方法为直接下采样.峰值信噪比(PSNR)是对图像平均的质量评价,而基于结构相似性(SSIM)的质量评价是一种视觉感知的评价,这2种方法广泛应用于图像质量评价中.表1给出采用不同方法把低分辨率图像重建为高分辨图像的PSNR和SSIM值.从数据上可以看出,本文算法的平均PSNR和SSIM值是最高的.通过数值对比发现,本文算法数值上优于对比算法.
此外,我们进一步探究区域划分时不同阈值对插值效果的影响.如图10所示,当阈值T分别取2.1,2.3,2.4时,图10(a)(b)(c)为对应的区域划分的效果图.由图10所示,不同的阈值对区域划分有较大的影响.图11为采用图10对应阈值插值后的图像,其对应的PSNR依次减小,可见区域划分的精确性会对插值图像产生一定影响.
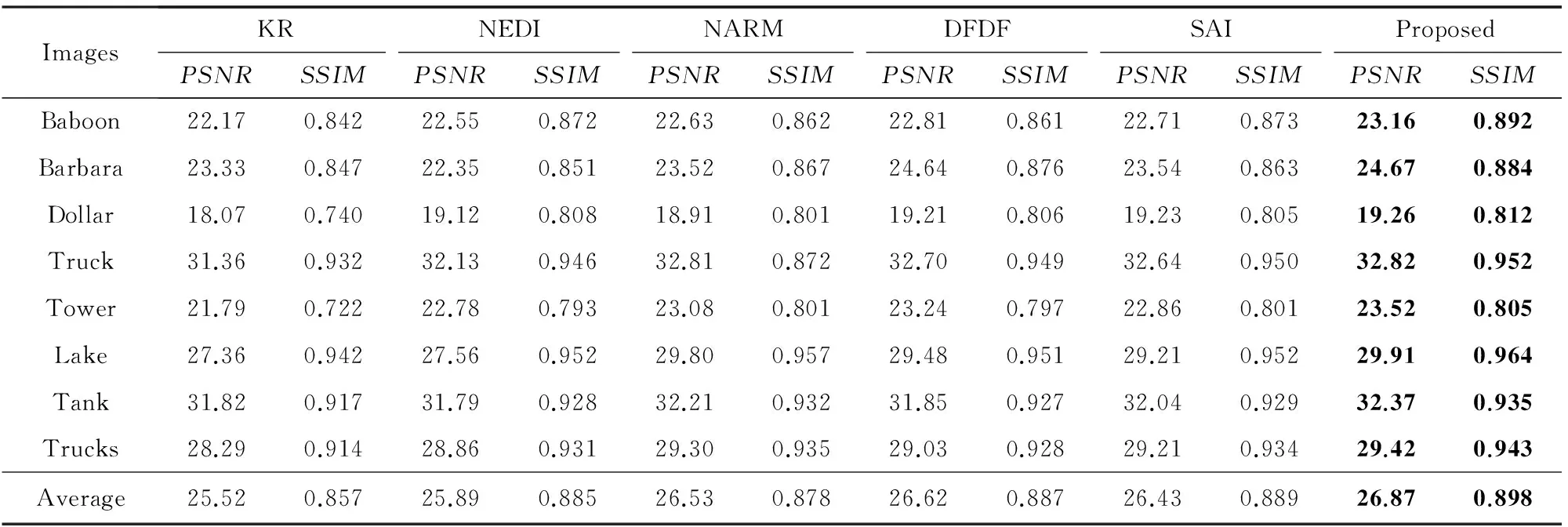
Table 1 The PSNR and SSIM Comparison of Different Algorithms
PSNR和SSIM是仅从数值上对二者之间的误差加以比较,同时也应当考虑到视觉效果.图12~19为测试图片视觉效果对比.在图12~16中,本文算法的插值效果图像明显增强,图像对比度有所提高.在图13中,所有比较算法均发生了纹理走样,而本文算法较其他算法走样较小,在下巴处围巾的处理效果明显好于其他算法.在图19中,NEDI和SAI在围栏处出现了噪点和变形,NARM在围栏处也有轻微噪点.本文算法与NARM视觉效果难分伯仲,但本文算法客观质量评价数值要好.图20~21为局部图像对比,放大之后的围栏处对比更加明显.针对纹理图像,如图21所示,本文算法无论是在客观数据上还是视觉质量上均取得一定优势.同时本方法也有一定的局限性,由于没有引入纹理的方向信息,在纹理方向的保持上稍显不足(如Barbara裤腿处).这也是我们下一步的工作计划.综上所述,标准测试图像的实验表明,本文算法与4种经典算法相比优势明显,尤其是包含纹理区域的高频部分.

Fig. 10 Edge detection by different threshold图10 不同阈值下区域检测效果图

Fig. 11 Interpolated images by different PSNR图11 不同峰值信噪比下插值效果图

Fig. 12 Results of “Brick”图12 Brick实验结果

Fig. 13 Results of “Barbara”图13 Barbara实验结果

Fig. 14 Results of “Rail”图14 Rail实验结果

Fig. 15 Results of “Dollar”图15 Dollar实验结果

Fig. 16 Results of “Lena”图16 Lena实验结果

Fig. 17 Results of “Truck”图17 Truck实验结果

Fig. 18 Results of “Xxal”图18 Xxal实验结果

Fig. 19 Results of “Cliff”图19 Cliff实验结果

Fig. 20 Regional results of “Rail”图20 Rail局部实验结果

Fig. 21 Regional results of “Xxal”图21 Xxal局部实验结果
4 结 论
本文基于图像局部分形维数特征分析提出一种混合插值算法.在传统有理函数插值的基础上,我们提出一种新的有理分形函数插值模型.模型中包含尺度因子和形状参数作为可调参数,通过插值点的结构信息调节参数,使得模型灵活性更高、精确性更好.在本文的插值算法中,首先通过计算局部分形维数,自适应地选取阈值对纹理区域和非纹理区域划分.分区域采用不同的插值函数进行插值.在有理插值模型中包含尺度因子,本文提出一种通过尺度因子与维数的关系精确计算尺度因子的方法.为了进一步提高图像的插值质量,我们通过极大化PSNR值对参数优化.实验结果表明:本文算法与其他5种经典插值算法相比优势明显,尤其在遥感图像和复杂纹理图像方面.

[1]Matsumoto S, Kamada M, Mijiddorj R O. Adaptive image interpolation by cardinal splines in piecewise constant tension[J]. Optimization Letters, 2012, 6(7): 1265-1280
[2]Zhang Caiming, Zhang Xin, Li Xuemei, et al. Cubic spline surface fitting to image with edges as constraints[C]Proc of the 20th IEEE Int Conf on Image Processing (ICIP). Piscataway, NJ: IEEE, 2013: 1046-1050
[3]Li Xin, Orchard M T. New edge-directed interpolation [J]. IEEE Trans on Image Processing, 2001, 10(10): 1521-1527
[4]Hiroyuki T, Sina F, Peyman M. Kernel regression for image processing and reconstruction [J]. IEEE Trans on Image Processing, 2007, 16(2): 349-366
[5]Zhang Lei, Wu Xiaolin. An edge-guided image interpolation algorithm via directional filtering and data fusion [J]. IEEE Trans on Image Processing, 2006, 15(8): 2226-2238
[6]Zhang Xiangjun, Wu Xiaolin. Image interpolation by adaptive 2-D autoregressive modeling and soft-decision estimation [J]. IEEE Trans on Image Processing, 2008, 17(6): 887-896
[7]Dong Weisheng, Zhang Lei, Lukac R, et al. Sparse representation based image interpolation with nonlocal autoregressive modeling [J]. IEEE Trans on Image Processing, 2013, 22(4): 1382-1394
[8]Jeong S, Yoon I, Jeon J, et al. Multi-frame example-based super-resolution using locally directional self-similarity[C]Proc of IEEE Int Conf on Consumer Electronics (ICCE). Piscataway, NJ: IEEE , 2015: 353-358
[9]Dou Nuo, Zhao Ruizhen, Cen Yigang, et al. Noisy image super-resolution reconstruction based on sparse representation [J]. Journal of Computer Research and Development, 2015, 52(4): 943-951 (in Chinese)(窦诺, 赵瑞珍, 岑翼刚, 等. 基于稀疏表示的含噪图像超分辨重建方法[J].计算机研究与发展,2015, 52(4): 943-951)
[10]Cao Shixiang, Jiang Jie, Zhang Guangjun, et al. Multi-scale image mosaic using features from edge [J]. Journal of Computer Research and Development, 2011, 48(9):1788-1793 (in Chinese)(曹世翔, 江 洁, 张广军, 等. 边缘特征点的多分辨率图像拼接[J].计算机研究与发展, 2011, 48(9): 1788-1793)
[11]Jha A K, Kumar A, Schaefer G, et al. An adaptive distance-based edge preserving interpolation algorithm for natural images[C]Proc of the Int Conf on Informatics, Electronics and Vision (ICIEV). Piscataway, NJ: IEEE, 2015: 1-5
[12]Zhu Shuyuan, Zeng Bing, Liu Guanghui, et al. Image interpolation based on non-local geometric similarities[C]Proc of 2015 IEEE Int Conf on Multimedia and Expo (ICME). Piscataway, NJ: IEEE, 2015: 1-6
[13]Zhang Yongqin, Liu Jiayang, Yang Wenhan, et al. Image super-resolution based on structure-modulated sparse representation [J]. IEEE Trans on Image Processing, 2015, 24(9): 2797-2810
[14]Hu Min, Tan Jieqing. Adaptive osculatory rational interpolation for image processing[J]. Journal of Computational and Applied Mathematics, 2006, 195(1): 46-53
[15]Carrato S, Tenze L. A high quality 2X image interpolator [J]. IEEE Signal Processing Letters, 2000, 7(6): 132-134
[16]Liu Yifang, Zhang Yunfeng, Guo Qiang, et al. Image interpolation based on weighted and blended rational function[G]LNCS 9009: Proc of Asian Conf on Computer Vision. Berlin: Springer, 2015: 78-88
[17]Varma M, Garg R. Locally invariant fractal features for statistical texture classification[C]Proc of the 11th Int Conf on Computer Vision. Piscataway, NJ: IEEE, 2007: 1-8
[18]Xu Yong, Ji Hui, Fermuller C. A projective invariant for textures[C]Proc of IEEE Computer Society Conf on Computer Vision and Pattern Recognition. Los Alamitos, CA: IEEE Computer Society, 2006: 1932-1939
[19]Xu Yong, Ji Hui, Fermuller C. Viewpoint invariant texture description using fractal analysis[J]. International Journal of Computer Vision, 2009, 83(1): 85-100
[20]Xu Yong, Yang Xiong, Ling Haibin, et al. A new texture descriptor using multifractal analysis in multiorientation wavelet pyramid[C]Proc of 2010 IEEE Conf Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2010: 161-168
[21]Xu Yong, Quan Yuhui, Ling Haibin, et al. Dynamic texture classification using dynamic fractal analysis[C]Proc of IEEE Int Conf on Computer Vision. Piscataway, NJ: IEEE, 2011: 1219-1226
[22]Xu Hongteng, Zhai Guangtao, Yang Xiaokang. Single image super-resolution with detail enhancement based on local fractal analysis of gradient [J]. IEEE Trans on Circuits and Systems for Video Technology, 2013, 23(10): 1740-1754
[23]He Sihua, Wu Zhen. Method of single image super-resolution enhancement based on fractal coding[C]Proc of the 3rd Int Conf Computer Science and Network Technology (ICCSNT). Piscataway, NJ: IEEE, 2013: 1034-1036
[24]Zhai Mingyue. Signal recovery in power-line communications systems based on the fractals [J]. IEEE Trans on Power Delivery, 2011, 26(3): 1864-1872
[25]Zhang Yunfeng, Bao Fangxun, Zhang Caiming. A weighted bivariate blending rational interpolation function and visualization control [J]. Journal of Computational Analysis and Applications, 2012, 14(7): 1303-1321
[26]Zhang Yunfeng, Bao Fangxun, Zhang Caiming. Local shape control of a bivariate rational interpolating surface with mixing conditions[C]Proc of the 8th Int Symp on Voronoi Diagrams in Science and Engineering (ISVD). Piscataway, NJ: IEEE , 2011: 200-205
[27]Duan Qi, Zhang Huanling, Zhang Yunfeng. Bounded property and point control of a bivariate rational interpolating surface [J]. Computers and Mathematics with Applications, 2006, 10(52): 975-984
[28]Novianto S, Suzuki Y, Maeda J. Near optimum estimation of local fractal dimension for image segmentation [J]. Pattern RecognitionLetters, 2003, 24(123): 365-374
[29]Zhou Jiyang, Xu Shengwei, Lin Nansen, et al. Spike detection based on fractal dimension[C]Proc of the IEEE Int Conf on Green Computing and Communications and IEEE Internet of Things and IEEE Cyber, Physical and Social Computing. Piscataway, NJ: IEEE, 2013: 1834-1838
[30]Viswanathan P, Chand A K B, Navascués M A. A rational iterated function system for resolution of univariate constrained interpolation [J]. Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales: Serie A Matemáticas, 2014, 109(2): 483-509
[31]Viswanathan P, Chand A K B, Navascués M. Fractal perturbation preserving fundamental shapes: Bounds on the scale factors [J]. Journal of Mathematical Analysis and Applications, 2014, 419(2): 804-817Zhang Yunfeng, born in 1977. PhD, professor in Shandong University of Finance and Economics. His main research interests include computer aided geometric design, digital image processing, computa-tional geometry, function approximation.

Yao Xunxiang, born in 1988. Master in Shandong University of Finance and Economics. His main research interests include imagevideo processing, fractal interpolation.

Bao Fangxun, born in 1968. PhD, professor of Shandong University. His main research interests include function approximation, computation geometry, computer aided geometric design and compute.

Zhang Caiming, born in 1955. PhD, professor and PhD supervisor in Shandong University. His main research interests include CAGD, CG, information visualiza-tion and medical image processing.
《信息安全研究》期刊简介
习近平总书记指出“没有网络安全就没有国家安全,没有信息化就没有现代化”.数字时代信息安全工具的大众化是不可阻挡的历史潮流.大众化的信息安全已经直接影响到我们每个人的利益,信息安全已成为国家、地方区域经济结构优化提升和转型发展的新机遇.在信息安全上升为国家战略、行业迎来崭新发展机遇形势下,《信息安全研究》期刊应时代而生.
《信息安全研究》是由国家发改委主管、国家信息中心主办的中文学术期刊,其宗旨是集中展示和报道国际、国内网络和信息安全研究领域研究成果及最新应用,传播信息安全基础理论和技术策略,服务国家信息安全形势发展需要.所刊登的论文均经过专家严格评审.
《信息安全研究》于2015年10月创刊发行.刊期为月刊,每期96页,由《信息安全研究》杂志社出版,国内外公开发行.
《信息安全研究》将以研究致以应用,搭建信息安全领域的学术交流平台,愿意和同行业及社会各界建立联系,友好合作,共赢美好未来.欢迎大家积极投稿、赐稿,洽谈合作.
投稿信箱:ris@cei.gov.cn
编辑部联系人:崔先生(185 0008 6481) 马先生(158 1058 2450)
Adaptive Interpolation Scheme Based on Texture Features
Zhang Yunfeng1, Yao Xunxiang1, Bao Fangxun2, and Zhang Caiming3
1(SchoolofComputerScience&Technology,ShandongUniversityofFinanceandEconomics,Jinan250014)2(SchoolofMathematics,ShandongUniversity,Jinan250100)3(SchoolofComputerScience&Technology,ShandongUniversity,Jinan250100)
A new interpolation model is proposed based on the bivariate rational interpolation. This model contains rational fractal interpolation and bivariate rational interpolation, which is identified uniquely by the values of iterated function system parameters (scaling factor and shape parameters). Due to efficient capacity of fractal in description of complex phenomenon, the fractal dimension is employed to texture analysis. Based on the analysis of local fractal dimension (LFD), a new local adaptive threshold method is proposed. And then images can be divided into texture region and non-texture region. As for texture regions, rational fractal interpolation is used to get high resolution images. Similarly, rational interpolation is used in non-texture region. Considering the parameters in rational fractal interpolation model, we propose a new method for calculating the scaling factor. Further, in order to improve the quality of interpolated image, shape parameters optimization technique is applied. Experimental results show that the presented model achieves very competitive performance with the state-of-the-art interpolation algorithms.
mixing interpolant; local fractal dimension; adaptive threshold; parameters optimizing; rational fractal
2016-07-13;
2016-12-09
国家自然科学基金项目(61373080,61672018,61402261,61373088,61272431,61332015);山东省高等学校优势学科人才团队培育计划 This work was supported by the National Natural Science Foundation of China (61373080, 61672018, 61402261, 61373088, 61272431, 61332015) and Fostering Project of Dominant Discipline and Talent Team of Shandong Province Higher Education Institutions.
包芳勋(fxbao@sdu.edu.cn)
TP391
