数字视频稳像技术综述
2017-09-15魏闪闪贺志强
魏闪闪 谢 巍 贺志强
1(北京航空航天大学计算机学院 北京 100191)2(联想研究院SoC中心 北京 100085)3 (联想集团生态系统与云服务业务群组 北京 100085)
数字视频稳像技术综述
魏闪闪1,2谢 巍2贺志强3
1(北京航空航天大学计算机学院 北京 100191)2(联想研究院SoC中心 北京 100085)3(联想集团生态系统与云服务业务群组 北京 100085)
(wswss11986@qq.com)
数字视频稳像(digital video stabilization, DVS)技术发展已历经30多年,随着设备计算能力的不断提高、算法研究的不断更新以及市场需求的不断驱动,数字视频稳像技术也随之不断发展,经历了从最初以计算简单为主的方案发展到以稳像效果显著为主的方案,再发展到计算简单并且效果显著的方案.通过对文献资料的整理分析,并根据技术发展的时间顺序,数字稳像技术被分类为传统方案和新兴方案.按照采用运动模型的不同,传统方案分为传统2D方案和传统3D方案;新兴方案分为新兴2D方案和借助传感器方案.对每类方案,首先对其采用的关键技术进行分析总结,然后列举这些关键技术在数字视频稳像中的应用实例.对数字稳像技术的发展进行了总结,最后对数字视频稳像技术的研究难点和发展趋势进行了展望.
数字视频;稳像;综述;传统方案;新兴方案
专业摄像师通常使用摄影车或者摄像机稳定器来保证拍摄视频的稳定性[1],而普通用户使用手持设备或者车载摄像头拍摄视频时,由于没有专业拍摄技能和专业稳像设备,拍摄的视频往往稳定性较差.当前,智能手机、平板电脑是主流的智能终端产品;穿戴式设备作为新生代智能设备正逐渐成为热点.它们一般都具备摄像功能,普通用户拍摄的视频常面临抖动问题.视频稳像技术的目的就是消除或减少视频的抖动,生成稳定的视频.
视频稳像技术总体可以分为三大类:机械稳像、光学稳像和数字稳像[2].
1) 机械稳像.常用于早期摄像机的稳像技术,采用稳定整个摄像机的方法,基于传感器(如陀螺仪、加速度仪等)的震动反馈.整个稳像系统较笨重且功耗高,因而不适于手持设备.
2) 光学稳像.光学稳像系统对光路进行重定向或者移动成像板来达到稳像目的.目前光学稳像系统大多依靠陀螺仪传感器来测量设备的移动或旋转量,通常是使用2个陀螺仪传感器来分别测量设备水平和垂直方向的角速率,二者的输出信号通过模数转换器(ADC)被转换为数字信息.
3) 数字视频稳像(digital video stabilization, DVS).除了机械稳像和光学稳像技术,还有2类视频稳像技术:电子稳像技术和纯数字稳像技术.这2类技术极其相似,区别仅仅在于设备抖动检测和运动估计方法.电子稳像技术使用硬件传感器(如陀螺仪等)来检测相机抖动,而纯数字稳像技术通过图像处理方法估计相机抖动.得到相机运动向量后,二者都进行运动补偿,并根据补偿的运动进行图像修补.本文将电子稳像和纯数字稳像技术统一称为数字稳像技术,因为二者都采用了数字方法进行图像修补,从而避免高功耗的电路控制系统,节省电路控制成本并降低了设备功耗.
表1对3种不同的视频稳像技术进行了对比.
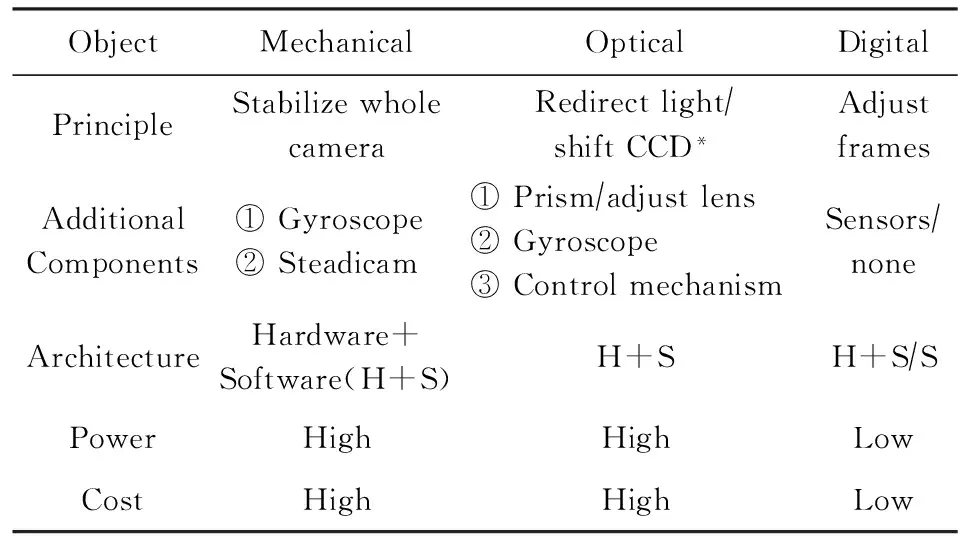
Table 1 Comparison of Video Stabilization Techniques
*:CCD means charge coupled device.
数字稳像解决方案是在图像生成后再进行视频抖动去除的数字技术方案.本文将其分为传统技术方案和新兴技术方案2种.传统技术方案分为传统2D技术方案和传统3D技术方案;新兴技术方案包括新兴2D技术方案和借助传感器的方案.对于每种解决方案,本文都先介绍技术原理并分析关键技术,然后综述应用实例.
1 传统数字稳像技术方案
数字稳像传统技术多采用3步法:运动估计、运动补偿和图像修补,如图1所示.根据运动模型的不同又可以分为传统2D方案和传统3D方案.前者采用2D运动模型,如平移[3]、2D欧氏变换[4]、仿射变换[5]等模型;后者采用3D运动模型,如投影变换模型.
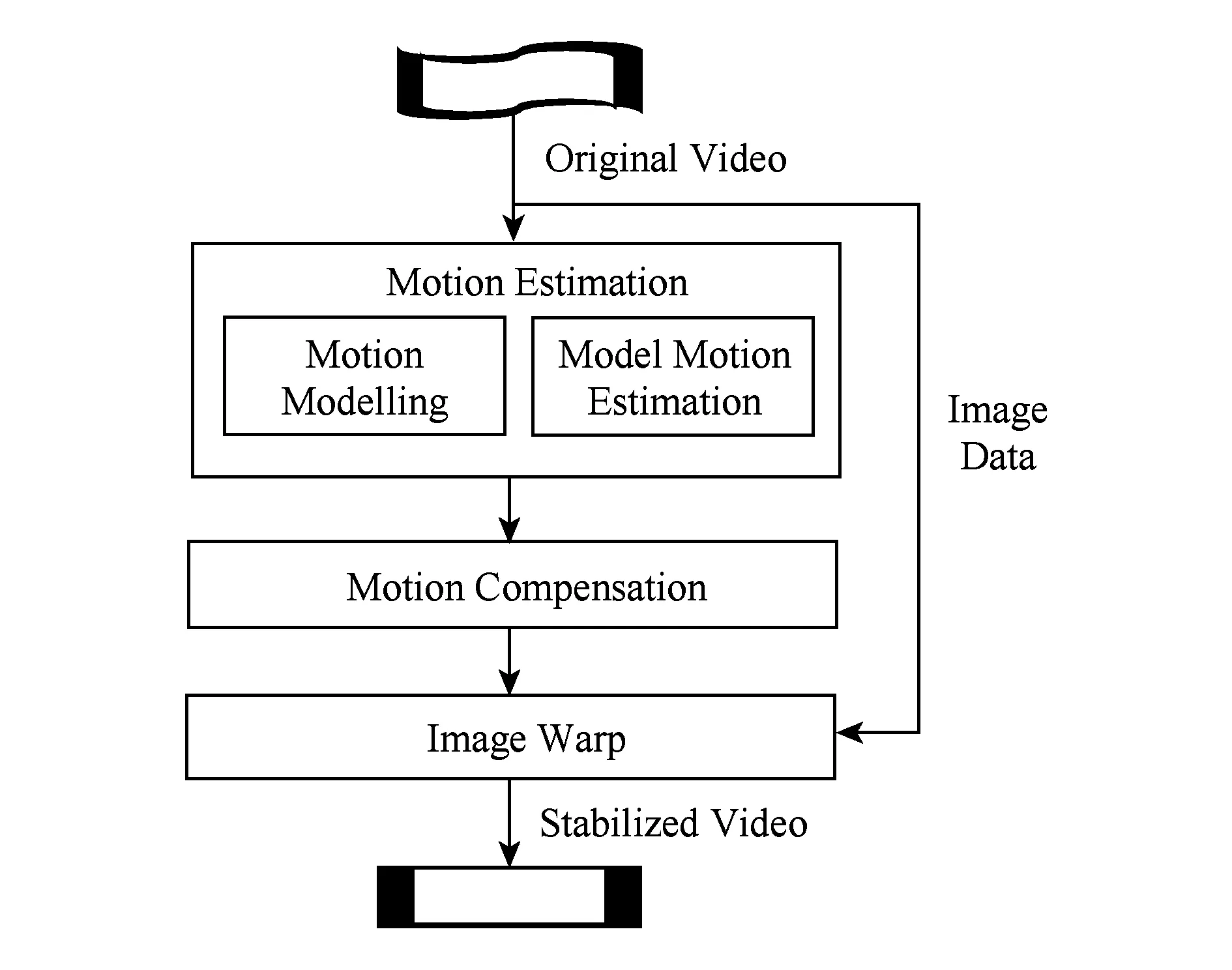
Fig. 1 Traditional DVS techniques图1 传统稳像技术方案图
1.1 传统2D稳像
传统2D稳像技术(如图2所示)采用“黄金3步法”:运动估计、运动补偿和图像修补.其解决方案众多,本文将它们划分为基于像素点的方案和基于特征点的方案两大类.
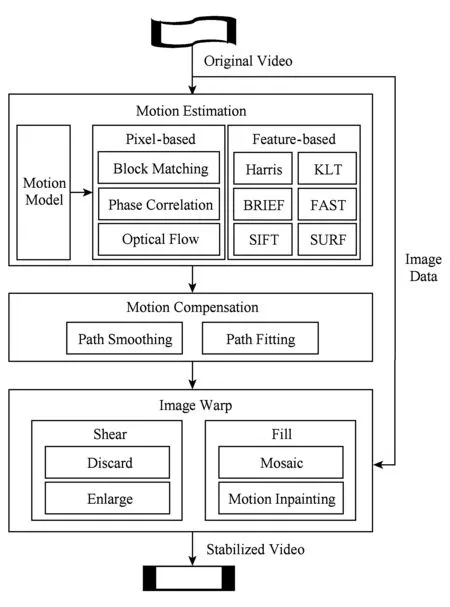
Fig. 2 Traditional 2D DVS techniques图2 传统2D稳像技术
1.1.1 运动估计
相机运动估计(camera motion estimation)是在特定相机运动模型下确定相机运动向量的过程,这些运动向量是描述2D图像(通常是连续的视频帧)间运动转换的量.相机运动向量可以使用平移模型来建模,也可以使用其他能够近似表示实际相机运动的模型来建模.相机运动向量是指与整张图像运动相关的全局运动向量,而它的估计常常通过局部运动向量来完成.局部运动向量指图像某一部分的运动向量,例如矩形块、任意形状块甚至是每个像素.传统2D稳像中的相机运动估计经常是首先进行局部运动向量的估计,然后通过这些局部运动向量来估计全局运动向量.局部运动估计方法可以分为两大类:基于像素点的方法(直接方法)和基于特征点的方法(间接方法).
1) 基于像素点的方法
此方法包括块匹配法、相位相关法、光流法等.
① 块匹配法
块匹配法是在数字视频序列中定位匹配块的一种运动估计方法,包括将视频帧分块、在附近帧(有时可能仅前一帧)中寻找当前帧中特定块位置.帧间匹配块的运动构成一个运动向量,所有匹配块的运动向量构成整个视频帧的运动向量.
块匹配法原理简单、实现方便,在传统2D视频稳像中拥有广泛的应用.Chen[6]使用基于块的参数运动模型进行视频稳像,其参数运动模型通过块匹配运动估计得到.在Chen[6]工作基础上,Bhaskar等人[7]使用块匹配法,提出一种基于移动平均滤波和Kalman滤波的运动补偿机制.
上述块匹配法方案实现简便,但在以下2种场景中效果并不好:一是场景中有快速运动物体或运动物体离镜头很近;二是场景较平坦变化少.这也是之后传统2D视频稳像应用块匹配法时重点解决的问题,即如何提高块匹配法的准确度.常用的策略包括以下3种:区分前景和背景、过滤局部运动矢量、优化全局运动估计算法.这3种策略也经常联合使用.
i) 区分前景和背景
例如Vella等人[8]使用经验法:假定图像中心某阈值内的区域为前景而其余靠近图像边缘部分为背景.同年作者还提出另外一种基于块匹配的算法[9],文章使用同样方法区分前景和背景,并使用加权平方直方图方法分别估计出前景和背景的运动矢量,然后根据组成前景和背景的块数来决定稳定前景还是背景.
ii) 过滤局部运动矢量
块匹配法获取的块运动矢量即为局部运动矢量,由于计算误差、匹配误差、运动物体等原因,直接使用它们进行全局运动估计往往误差较大.常用的局部运动矢量的过滤策略有:去除低信噪比(signal noise ratio, SNR)块(过于复杂的块)、去除平坦块(无明显特征的块)、去除绝对差和(sum of absolute difference, SAD)值过低块、去除重复类型块等.
例如,Yang等人[10]为去除局部运动向量(local motion vector, LMV)的偏值,在稳像算法中去除了缺少特征点、低SNR以及重复类型的块.算法全局运动向量(global motion vector, GMV)通过取所有LMV均值的简单操作来估计.Battiato等人[11]使用块匹配法获取局部运动矢量,然后使用简单快速的过滤规则去除偏值,获取可靠的局部运动矢量.这些规则包括初级过滤规则和记忆过滤规则,前者是通用的过滤规则,文章贡献点在于后者:对于当前帧中新块的局部运动矢量,拒绝其中一定比例来降低大块运动物体的影响.
iii) 优化全局运动估计算法
常用策略包括权值法、统计法、聚类法等.
Chen等人[12]对局部运动矢量使用聚类过程确定全局运动向量:构建局部运动向量的直方图,然后通过加权平均方法计算全局运动向量.Puglisi等人[13]使用基于选举的方法来从局部运动向量计算全局运动向量,方案还将穷尽搜索与卷积投影误差函数结合来获取局部运动向量.Tang等人[14]使用一种基于加权直方图的统计方法来计算全局抖动运动向量,最后通过累加得到整体全局运动链.
② 相位相关算法
相位相关算法是一种非线性、基于傅氏功率谱的频域相关算法,其理论基础是傅里叶变换.它只取互功率谱中的相位信息,减少了对图像内容的依赖性,位移检测范围较大,有很高的匹配精度;同时,相位相关技术对图像灰度依赖较小,因而具有一定抗干扰能力.相位相关法用于运动估计的解决方案有很多[15-25],用于视频稳像的应用也很多.
Erturk[26]使用基于子图像相位相关的全局运动估计方法进行视频稳像,算法首先将图像分为4个子图像,然后对每个子图像使用相位相关法进行局部运动估计,最后基于4个子图像的局部运动来完成全局运动的估计.同年,作者使用相位相关和对数极坐标幅度谱表示法来获取运动参数(平移、旋转和缩放),然后使用Kalman滤波器进行运动平滑来进行视频稳像[27].Sanjeev等人[28]提出一种基于Fourier-Mellin域相位相关的稳像算法,算法分粗粒度和精细粒度2个阶段.Jia等人[29]的稳像算法首先对Fourier-Mellin变换图像通过相位相关法获得旋转和缩放参数并对目标图像进行旋转和缩放,然后使用相位相关法来计算空间平移参数完成运动估计.Zhang等人[30]基于中心子图像的相位相关法提出一种适用于车载摄像头的视频稳像方法.
③ 光流法
光流法的概念最早由美国心理学家Gibson在20世纪40年代提出,当时是为了实现描述动物运动的视觉仿真[31].在图像处理领域,光流描述的是图像中亮度的视运动,它计算不同时刻的2张图像上每个像素的运动情况.Barron等人[32]对微分法、匹配法、基于能量法和基于相位法光等多种知名流算法从光流测量的准确度、可靠性和密度等方面进行了其性能的研究对比.
Lucas与Kanade[33]为光流法在视频稳像中的应用提供了基础.作者将图像进行块划分,并假设若块足够小,则块中各像素的运动向量是一致的,此时可以使用块中心的运动矢量代表块中各像素的运动矢量.基于上述假设,Chang等人[34]首先基于Lucas-Kanade法计算连续帧间的光流值,接着将光流域结果应用到简化的仿射运动模型中进行相机运动估计并完成视频稳像.Chang等人[35]首先使用光流法计算图像局部运动向量,求出每一个像素的运动速率,然后应用最小二乘法估计平移和旋转运动参数,最后运用上述运动参数去除抖动.Cai等人[36]使用Lucas-Kanade金字塔法[37]进行光流估计,并使用排序局部运动直方图来估计相机运动,这利用了每个运动直方图的峰值位置对估计误差不敏感且不受运动物体影响的特点.之后作者又研究提出使用增量光流法(delta optical flow)的视频稳像方案[38],以增强存在大面积运动物体的场景视频稳像的稳健性.文章使用光流排序队列和增量光流法来选择特征点以避免影响运动物体,进而避免全局运动估计受估计误差和运动物体影响.
2) 基于特征点的方法
特征点检测法将高维的图像数据进行简化表达,常见的特征点检测方法有角点检测法、斑点检测法、边检测法等.在视频稳像应用中,角点检测和斑点检测是最常用的技术.
角点也叫极值点,是指在某方面属性特别突出的点.视频稳像方案中常用的角点检测算法有Harris算法[39]、FAST(features from accelerated segment test)算法[40]以及KLT(Kanade-Lucas-Tomasi)算法[33,41]等.斑点检测法检测图像中比它周围像素灰度值大或小的区域.视频稳像中实现斑点检测的主要方法是尺度不变特征转换方法(scale-invariant feature transform, SIFT)[42]和加速稳健特征算法(speeded up robust features, SURF)[43].SIFT算法对旋转、尺度缩放、亮度变化保持不变性,对视角变化、仿射变换、噪声也保持一定程度的稳定性;SURF算法作为SIFT算法的加速版,基本实现了实时处理,它能提高速度的理论基础是使用积分图像haar求导.
Amisha等人[44]对FAST,BRIEF,SIFT,SURF等特征点检测方法进行了分析对比.
Censi等人[45]通过KLT特征点跟踪方法计算相机运动补偿来进行视频稳像,并使用图像形变结果来帮助预估特征点的位置,以增强特征点跟踪的可靠性.Hu等人[46]采用2D仿射模型,使用SIFT特征点和最小二乘法来进行运动估计并完成视频稳像.Yang等人[47]将粒子滤波器在目标跟踪中的传统应用扩展到相机运动的投影仿射模型中.算法首先使用SIFT特征点跟踪法进行全局运动估计,然后对SIFT特征点进行粒子滤波来整合图像强度信息,最终得到更加平滑的相机运动估计.Shen等人[48]使用基于SIFT特征点的主成分分析法(principal component analysis, PCA)来降低特征点空间的维度,获取到PCA-SIFT特征点用来估计帧间抖动运动.之后使用粒子滤波框架来进行相机运动滤波完成稳像功能.Pinto等人[49]使用SURF作为帧间跟踪的稳定特征点来进行2D仿射运动参数的全局运动估计,使用离散Kalman滤波器来平滑运动向量,最终得到稳定视频.Zhou等人[50]对每帧图像提取并跟踪SURF特征点,使用RANSAC算法来估计仿射运动参数,并利用自适应运动向量积分法进行相机抖动运动平滑,最终完成视频稳像.Zhang等人[51]使用类似的方法,应用SURF特征点进行局部运动向量估计,并用稳定后的帧来修补抖动帧,完成全帧视频稳像.Zheng等人[52]使用SURF作为特征描述子,利用RANSAC算法提纯特征点,并使用最小二乘法估计2D仿射模型运动参数,最后使用带有自适应阻尼系数的运动矢量积分法来平滑全局运动,最终完成视频稳像.
基于像素点和基于特征点的方法各有优缺点,关于它们的讨论最终以2篇结论性的论文而收官:Irani和Anandan所著基于像素点方法的综述[53]以及Torr和Zisserman所著基于特征点方法的综述[54].
1.1.2 运动补偿
在稳像技术中,相机运动补偿是用来产生新的相机运动的算法,它抑制抖动生成更加稳定的相机运动.对于2D视频稳像来说,运动补偿机制接收相机2D运动数据,经算法计算产生新的平滑2D运动数据.运动补偿总体上分为2类方案:运动路径平滑和运动路径拟合.
1) 运动路径平滑
稳定视频所对应的相机运动数据应该也是平滑的,相反抖动视频的相机运动数据存在小幅抖动的“噪声”.从数字信号处理角度来说,运动平滑就是消除这些运动噪声.视频稳像方案中常用的平滑滤波器有移动平均(moving average)滤波器、Gaussian滤波器、Kalman滤波器[55]、粒子滤波器以及其他多项式滤波器[56].
① 移动平均滤波器
移动平均滤波器是一种低通滤波器,它将连续的采样数据看成一个长度固定的队列,每完成一次新的处理,队列向前移动,即去掉队列首数据,队尾插入新数据.这种滤波方法简单易行,在视频稳像方案中经常采用.Chen[6]使用了简单的移动平均滤波器进行运动平滑.无限冲击响应(infinite impulse response, IIR)滤波器属于移动平均滤波器,它也被称为运动向量整合法(motion vector integration, MVI).Ko等人[3]在其视频稳像方案中,基于位平面匹配法使用一阶IIR滤波器进行运动平滑.Yang等人[10]使用简单的一阶自适应IIR移动平均滤波器进行运动平滑,为实现自适应性,滤波器通过动态机制来确定平滑因子大小:通过连续3帧图像的全局运动矢量来判断当前抖动情况,并赋予其不同大小.Erturk[57]对MVI法进行了分析总结.
② Gaussian滤波器
Gaussian滤波器是根据Gaussian函数的形状来选择权值的线性平滑滤波器,对抑制服从正态分布的噪声非常有效.而相机运动数据中的抖动可以建模为符合Gaussian分布的噪声,因此非常适合使用Gaussian滤波器来进行滤波,抑制噪声的过程即为平滑运动的过程.理想的Gaussian滤波器在计算机中实现复杂,因此有时采用效果近似同时计算简单的滤波方法,如Binomial滤波[58]等.Yasuyuki等人[59]使用Gaussian内核完成运动补偿,之后Hu等人[46]、Xu等人[60]在各自稳像方案中使用了类似方法进行运动补偿.
③ Kalman滤波器
Kalman滤波器是一种最优化自回归数据处理算法,能够在线性Gaussian模型的条件下对目标的状态做出最优估计,得到较好的跟踪效果.非线性滤波问题常用的处理方法是利用线性化技巧将其转化为一个近似的线性滤波问题.因此可以利用非线性函数的局部性特性将非线性模型局部化,再利用Kalman滤波算法完成滤波跟踪.扩展Kalman滤波(extended Kalman filter,EKF)就是基于此思想,将系统的非线性函数做一阶Taylor展开得到线性化的系统方程从而完成对目标的滤波估计等处理.
Kalman滤波器用于视频稳像的应用有很多.Erturk[26-27]使用Kalman滤波器进行运动平滑,并实现实时稳像.Erturk[61]将全局运动表示为常量加速运动和常量角速度运动,然后使用标准Kalman滤波框架去除短时间图像抖动,保留平滑运动,实现稳像.Litvin等人[62]使用概率估计框架检测抖动,将帧间相机抖动视为相机本意运动的噪声观察,并使用Kalman滤波框架来估计获取用户本意的运动参数完成视频稳像.Gullu等人[63]的稳像方案使用2个并列的Kalman滤波器、1个稳定Kalman滤波器和1个参考Kalman滤波器.前者用于平滑相机运动,后者引入模糊自适应机制来调节控制运动补偿偏移量.Wang等人[64]考虑运动平滑程度问题:过度补偿会导致图像空白边缘太大,影响图像质量.为解决此问题,作者将此约束作为额外的状态更新方程包含到Kalman滤波过程中,将运动轨迹稳定问题转化为该约束下最优化问题.
④ 粒子滤波器
粒子滤波是20世纪90年代发展起来的一种新滤波算法,其核心思想是通过从后验概率中抽取的随机状态粒子来表达其分布,它克服了EKF的缺点,在非线性、非高斯系统中表现出优越性.Gordon等人[65]为粒子滤波在视频稳像中的应用奠定了基础.Yang等人[66]首先将粒子滤波法用于视频稳像,之后又对其进行了改进[67].
2) 运动路径拟合
与运动路径平滑不同,运动路径拟合模仿专业电影摄影路径,例如直线、抛物线等.这种方案能比运动路径平滑获取更加稳定的运动补偿结果,因为它不仅能去除高频抖动,还能去除路径中的无效低频抖动.Chen等人[68]根据专业拍摄使用三脚架时相机运动路径接近折线(polyline)的特点,采用拟合折线法来进行运动补偿.其运动补偿方案首先使用Kalman滤波器去除高频抖动,然后在此基础上进行折线路径拟合,从而去除无效低频抖动.Zhang等人[69]使用低级和高级双通道优化方法约束相机路径进行运动补偿.方案首先进行低级路径优化,自动检测画面干扰并消除,再使用L1优化框架来生成初级补偿相机路径;之后将相机路径分解为缩放、旋转、平移分量,通过分析这些分量将路径分段,并为每段路径拟合更简单的专业拍摄中使用的运动模型来达到运动补偿目的.
当然,运动路径拟合法在获取更平滑运动补偿结果的同时,也会增加需要修补的缺失区域,即增加了图像修补过程的难度.
1.1.3 图像修补
在相机运动估计和相机运动补偿完成后,得到一个新的、平滑的相机运动链.图像修补操作根据新运动链在所采用的运动模型对原始图像进行形变处理,得到包含丢失部分(空白边缘)的稳定后图像.此时处理方法有2种:剪切处理和填补空白边缘.前者处理简单,但改变了图像尺寸;后者保存图像尺寸,最常用的方法是马赛克法(mosaicing),马赛克法根据图像所要修补区域周边的像素信息来完成图像修补.Litvin等人[62]使用马赛克法来填补空白边缘,作者声明他们最先使用马赛克法对稳定后的视频帧进行图像修补操作.Yasuyuki等人[59]的运动修补法是2D方案中的经典图像修补方案,它将运动估计的思想融入到图像修补中:根据当前帧或相邻帧中像素的运动数据来估计空白区域的像素信息.Tang等人[14]和Yoo等人[70]的稳像方案中,都综合马赛克法和运动修补法进行图像修补.Chen等人[68]提出的方案对于动态场景缺失域修补使用运动修补法,对于静态场景缺失域修补使用像素修补法:根据仿射变换模型,直接从其他帧中寻找对应像素点复制而来.
1.2 传统3D稳像
相机在3D空间中运动,而图像的像素在2D平面运动.对于人眼而言,对于视频运动的感知直接来源于像素的运动.然而,事实证明,对2D图像像素进行简单直接的平滑操作并不能获得很好的稳像效果,因为仅对2D图像像素进行的操作忽略了相机本身的3D空间运动信息.
2D图像空间和相机3D空间之间是存在运动关联的,3D稳像方案同时考虑二者,采用相机3D运动模型,而非简单的2D运动模型来表示相机运动.运动估计方式的不同也决定了运动补偿方式的不同,以及相应的图像修补方式的不同.因为不同运动模型下2D图像像素运动和3D真实相机运动的映射关系不同.
视频3D稳像是通过2D图像信息来重构相机的3D运动信息(有的方案还会恢复像素点的3D位置信息);然后对恢复的相机运动进行平滑处理去除抖动,生成平滑后新的相机运动信息;最后根据这些新的运动信息(和像素点3D位置信息)来完成图像的修补.
3D稳像方案也采用“黄金3步法”:相机3D运动估计、相机3D运动补偿和2D图像修补.与传统2D稳像方案不同的是,3D稳像基于相机3D运动模型来解决稳像问题,通常采用针孔相机模型下的投影变换运动模型[71],传统3D稳像流程如图3所示.
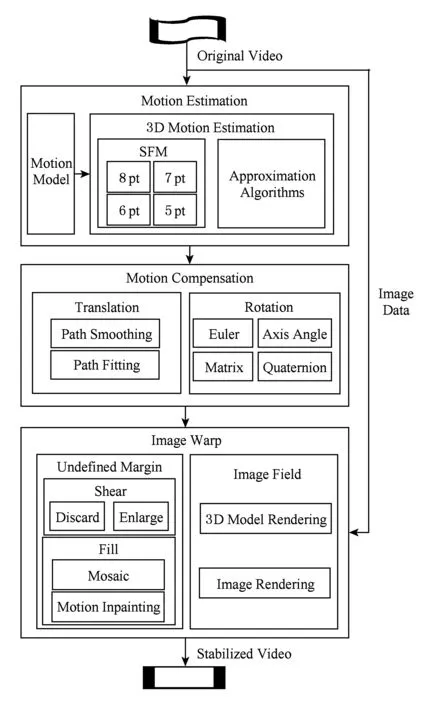
Fig. 3 Traditional 3D DVS techniques图3 传统3D稳像技术
1.2.1 运动估计
3D稳像中相机3D运动估计即为在针孔相机投影变换模型下,从图像信息中恢复相机姿态的问题.3D运动参数包括平移和旋转参数,运动到结构算法(structure from motion, SFM)正是用来解决此问题的:从2D的图像序列中恢复出相应的3D信息,其中包括成像相机的运动参数以及场景的结构信息.SFM问题可以通过双视角、三视角或者多视角方案来解决[71],而3D稳像中使用的是双视角方法,即给定2个视角相机的图像,恢复2个成像时间相机的位置信息.SFM算法的前提是特征点匹配的问题得以解决,这正是2D稳像方案中基于特征点的运动估计的相关技术.SFM算法将3D运动估计转化为在若干视角下,使用若干特征点对来构建方程组求解相机外参的问题.求解方法包括8点算法[72]、7点算法[71]、6点算法[73-74]、5点算法等[75-76],Brückner等人[77]对这几种算法进行了系统的实验比较.SFM算法计算相对复杂,早期的稳像方案并没有采用这种方法.
Wang等人[78]使用SIFT特征点和RKHS图形匹配技术[79]进行SIFT特征点匹配,在旋转角度极小的假设前提下(作者认为帧间平移与旋转量相对较小),对旋转矩阵进行简化,这样精简了相机3D运动的估计过程.Zhang等人[80]提出一种基于相机3D运动模型的稳像方案,将视频稳像建模为平滑和相似约束条件下的二次成本函数,并通过对稳像过程中平滑性和相似性一对矛盾的平衡来获取视频的稳定性.Liu等人[81]提出的3D稳像方案被视为近些年来最经典的3D稳像方案,它首先使用SFM算法恢复相机3D原始运动以及3D场景点云,然后进行自动或交互的运动平滑来获取稳定的相机运动,最后使用3D场景点云和参考帧图像完成运动平滑后的图像形变修复.Lee等人[82]在Liu等人[81]的工作基础上,提出了基于兴趣域(region of interest,ROI)形变的稳像方法.方案首先筛选特征点,筛选后的特征点所在区域是抖动最严重区域ROI并予以重点处理,仅使用ROI区域的特征点作为参数来进行Liu等人[81]的算法.如果ROI区域特征点在筛选后剩余量少于设定的阈值,则算法变为Liu等人[81]的方法.Ryu等人[83]借助零均值归一化互相关匹配法(zero mean normalized cross-correlation,ZNCC)和KLT算法来进行相机3D运动估计,提出一种类人眼的视频稳像方案.文章还引入了受启发于人眼前庭动眼反射的方法(vestibulo ocular reflex,VOR)用于加快运动估计的速度.
1.2.2 运动补偿
对于3D视频稳像来说,平滑滤波器接收相机3D运动数据,经算法计算产生平滑后的3D运动数据.与2D运动不同,3D运动数据不仅包括相机位置信息,还包括相机方向信息矩阵R.因此,3D运动补偿要比2D运动补偿复杂.在针孔相机投影变换模型下,相机3D运动数据中的位置信息向量T和方向信息矩阵R为2个独立运动,因此二者的运动补偿可以分开进行.位置信息向量T的运动补偿技术原理与2D运动补偿类似,区别在于3D位置向量多一个分量.3D运动补偿的难点在于方向信息的运动补偿.
尽管3D位置信息平滑有很多方法,但这些方法不能简单应用到3D方向信息的平滑中,因为3D方向信息是非线性的.方向信息的表示有若干种形式,包括欧拉角、轴角、旋转矩阵、四元数等.
这些表示方法中,四元数因其诸多优点成为目前最流行的形式.四元数平滑的难点在于四元数空间的非线性属性,这导致无法直接使用通用线性时不变(linear time-invariant, LTI)滤波器进行平滑.为解决此问题,研究者提出一些方法.Azuma等人[84]提出将四元数4个分量分开处理,然后再重规格化(re-normalize)滤波响应来保证单位性.重规格化的缺点是会带来副作用,例如奇点、畸变等.另外一种方法是使用全局线性化方法,例如使用指数与对数映射法[85-87]来避免重规格化.这种方法的缺点是当输入信号接近奇点时会产生不确定结果.Shoemake球面线性插值 (spherical linear interpolation, SLERP)方法[88]的提出为四元数平滑滤波提供了新方案,之后基于此的非线性滤波方法也逐渐提出[89-90].Lee等人[91]提出一种滤波方式,将旋转数据转为向量空间上的表达,然后在向量空间进行滤波,最后将滤波后的向量空间数据再反转为旋转空间数据.这种方法是一种局部线性化方法,它对旋转数据的表示方式没有限制,是一种通用的旋转数据滤波方式.Morimoto等人[92]使用单位四元数来表示帧间旋转量,并使用EKF来完成运动估计和运动补偿.Liu等人[81]将3D运动向量分为平移和旋转分量来分别平滑,旋转分量使用了Lee[91]的方法.
1.2.3 图像修补
3D相机运动补偿完成后,得到了平滑的运动轨迹,稳像最后一步即是根据新的轨迹渲染生成新的稳定的图像.3D稳像中常用的图像修补的类型总体包括两大类:一是图像空白边缘的处理;二是基于图像域的处理.前者与传统2D稳像方案中的技术一样.基于图像域的处理方案,目前流行的有2种:一是基于3D模型的渲染(3D model-based rendering);二是基于图像的渲染(image-based rendering, IBR).Kang[93]对基于3D模型的渲染方法与基于图像的渲染方法进行了比对.
1) 基于3D模型的渲染
基于3D模型的渲染是根据已重构(或近似重构)的场景3D模型来计算新视角下的场景图像.3D场景模型可以使用CAD建模工具获取,也可以从实际数据中通过场景重构算法计算得到.Liu等人[81]为防止修复的图像产生畸变,提出保存内容的形变技术(content-preserving warps),将稀疏场景点的位移视为软约束条件.此方法稳像效果优异,被视为3D稳像的经典;缺点是计算复杂,运算消耗大.Zhang等人[80]3D稳像方案中的图像修补阶段也采用了基于3D场景点的渲染技术.
2) 基于图像的渲染
与基于3D模型的渲染方法不同,基于图像的渲染通过同一场景不同视角的图像来插值成一副新视角的图像,是一种新视角插值技术.图像渲染技术研究已有多年,Kang[93]将图像渲染技术按像素索引属性分为四大类:基于非物理图像映射法、马赛克法、深度采样插值法以及几何有效像素重投影法.这些方法的一个缺点是鬼影效果(ghosting effect),这是因为IBR方法假设前提是场景是静态的,当在不同视角下场景中有明显运动的物体或光照变化时,合成的图像会有“重影”.因此本技术直接使用于3D稳像方案时,在动态场景下稳像效果会带来明显副作用.要克服此问题,一种直观的方案是在动态场景下检测运动物体并提出,然后只对剩余的静态背景进行图像渲染,最后将运动物体重新合成到场景中去.然而这些步骤中的每一步都是巨大的挑战,实现困难.为解决IBR的这个问题,研究者在IBR基础上提出了很多改进方案.Shade等人[94]提出一种使用分层深度图像的渲染方法,允许单个像素可以进行多层深度编码,每层内深度固定.Kang等人[95]在1999年提出一种“多层IBR算法”,将视频分为多层,每层均进行独立的重投影,并最终合并为一帧图像.Buehler等人[96]在2001年提出非结构流明图渲染方法,它主要作为一种IBR渲染框架来扩展当时的IBR算法;之后又提出一种非度量IBR算法[97],在上述算法基础上进行了改善,将所有的测量在图像域进行,而非度量域.文章提出的基于图像渲染技术的视频稳像方案被视为最早的3D稳像方案.Buehler等人指出基于图像的渲染技术用于视频稳像的3个必备技术条件:1)帧间匹配特征点;2)帧间插值;3)场景中虚拟相机轨迹操作.
1.3 本节小结
传统稳像方案采用运动估计、运动补偿、图像修补“黄金3步曲”.根据运动模型选取的不同,本节将传统稳像方案划分为传统2D稳像和传统3D稳像并按照3个关键步骤分别进行了综述.相机运动模型选择的不同,导致3个关键步骤都不尽相同.传统2D稳像方案原理简单、计算量小,但稳像效果一般;传统3D稳像方案效果好,但计算复杂.二者的应用场景也会根据效果和速度这一对矛盾进行适当选取.
2 新兴数字稳像技术方案
随着智能终端时代的来临,传统稳像技术已逐渐无法满足智能设备的应用需求,新兴技术正逐渐涌现.一方面,研究者在寻求新兴的2D稳像技术,不再局限于传统稳像“3步曲”;另一方面,借助智能设备中的微机电传感器,研究者在寻求新兴的基于传感器的稳像技术,使运动估计过程更加有效.
2.1 新兴2D稳像
与传统2D稳像方案不同,新兴2D稳像既不遵循“黄金3步曲”,也不像传统3D稳像那样重建完整3D相机运动,而是使用新兴的2D方法来尽力获取与3D方法相似的防抖效果.这些方案不尽相同,但共同点是将相机3D运动重建过程的约束条件放松,绕过复杂的3D重建操作.新兴2D稳像按其采用的策略可以划分为特征点轨迹法和几何约束条件法.
1) 特征点轨迹法
此方法将相机3D运动重建问题的约束放宽,转化为处理相应2D图像空间特征点轨迹的问题.
Wang等人[98]用贝塞尔曲线表示特征点轨迹,提出一种时空优化法,将稳像问题转化为平滑特征曲线并避免视觉畸变的时空优化问题.作者认为贝塞尔曲线表示法能够有效平滑特征轨迹,同时能够减少优化问题中的变量数目,从而提高稳像效率.Lee等人[99]提出,可靠的跟踪特征点通常落在背景区域;大部分相机运动已经足够稳定,而无需进行运动平滑导致过多的空白边缘.因此作者使用稳健特征轨迹进行视频稳像,在保证视频稳定的前提下尽量控制空白边缘,力求二者的平衡.文章使用的特征提取算法融合SIFT算法和粒子视频法,利用SIFT算法空域运动的连续性减少误匹配以及粒子视频法轨迹时域运动的相似性保证大范围特征跟踪.Liu等人[1]根据3D刚体场景图像的运动轨迹矩阵可以近似表示在低维度子空间内[100]的理论,提出子空间稳像法.方案先使用标准2D特征点跟踪方法建立稀疏场景点的2D轨迹矩阵;然后对其做移动分解变换(moving factorization)来寻找对输入运动的一个时变子空间近似,以将运动估计局部表示为2部分的乘积:一是称为“特征轨迹”的基向量,二是将特征点描述为这些特征轨迹线性组合的系数矩阵;之后对特征轨迹进行运动平滑,将平滑后的特征轨迹与原始系数矩阵重新相乘来得到平滑后的输出轨迹;最后使用渲染方案完成视频稳像.Ryu等人[101]使用KLT跟踪器来跟踪特征点轨迹,然后使用Kalman滤波器来生成平滑特征点轨迹,最后在2D仿射模型下采用双线性插值法进行图像拼接完成稳像.Ringaby等人[102]使用KLT跟踪器对Harris角点进行跟踪,将相机旋转参数化为带有节点的连续曲线,并使用非线性最小二乘法来求解曲线参数,然后平滑此曲线来完成相关旋转序列的平滑.Liu等人[103]将“as-similar-as-possible”的思想[81]引入到相机运动估计中来提高运动估计的鲁棒性,提出一种多重的、时空可变的相机路径模型,让不同位置可以有独自的相机路径.此方法无须进行长时间特征轨迹跟踪或稀疏3D重建,而使用多相机路径建模相机运动,并使用基于网格的空间可变运动表示法以及自适应的时空路径优化法.Zhang等人[69]使用KLT跟踪器来跟踪特征点轨迹,并根据特征点显著度(saliency)来判断其是否位于运动物体,去掉高显著度的特征点后使用仿射模型来估计相机运动路径,并提出一种“双通道”优化方法进行运动补偿完成视频稳像.基于Liu等人[103]的多路径方案,Bai等人[104]提出一种用户辅助的视频稳像方案,将跟踪到的特征轨迹进行聚类并显示,用户可以根据需要选择或去除不合适的特征轨迹类,用户还可以直接自定义视频帧中某个区域如何进行形变,这可以帮助减少视频稳像后的畸变,最后根据用户对于特征轨迹的筛选和指定区域的形变来生成稳定视频.Wang等人[105]使用多平面结构实现视频稳像.文章首先进行平面检测:根据多视角几何的平面单应变换产生的重投影误差来将特征轨迹进行分类,相同类型的特征轨迹位于同一平面;然后对每个平面进行单独特征轨迹平滑操作;最后使用保存内容的图像形变[82]来融合图中所有平滑过的平面,生成最终稳定视频.
2) 几何约束条件法
几何约束条件法不直接进行相机3D运动重建,而是寻找一些重要的几何约束条件,将复杂3D运动重建过程近似为遵循这些约束条件的求解问题.
Goldstein等人[106]提出一种稳像方案,将计算复杂的3D运动恢复简化为简单的像素点与极线的几何约束条件.这种方法可以获得接近3D方法的稳像结果,同时增强了稳健性并减小了运算开销.方案首先使用KLT法来跟踪特征点,然后计算包含了相机运动信息的基础矩阵,再使用Gaussian滤波器完成估计平滑,最后使用对极点转移法[107]来确定平滑后特征点的位置.Hsu等人[108]基于单应一致性约束提出一种稳像算法.作者认为稳定视频应满足2个条件:一是平滑的运动轨迹,二是连贯的帧间过渡.传统方法大多只解决第1个问题,它们需要合适的、特定场景的参数设置,无法通用于不同场景.针对此问题,作者使用KLT跟踪器跟踪Harris角点来进行特征点匹配,并基于单应一致性的几何约束来直接提取最佳平滑轨迹并使得帧间过渡均匀分布.
2.2 借助传感器稳像
随着微机电(micro-electro-mechanical system,MEMS)传感器近些年在智能设备中的逐渐普及并且精度越来越高,基于MEMS传感器的视频稳像的新兴方案逐渐出现.传感器用来获取相机运动极大简化了运动估计的计算量,且可以应用在特征点不明显甚至无法检测到特征点情况下,提高视频稳像的稳健性.
Ryu等人[109]使用惯性传感器获取3D旋转信息来预测特征点初始位置,使其尽量接近跟踪搜索范围,以加速特征点跟踪.方案将传感器与KLT跟踪器结合,采用相机3D旋转模型,并且引入受启发于人眼前庭动眼反射的方法来完成视频稳像.Karpenko等人[110]声称,他们率先使用陀螺仪来解决手机应用的数字视频防抖.作者使用陀螺仪获取相机3D旋转信息,并使用相机3D旋转模型建模解决视频稳像问题.作者指出,使用3D旋转运动模型的原因有3点:1)加速度传感器需要二次积分运算来获取位移信息,然而二次积分带来的误差太大,严重影响平移参量估计的准度;2)即便获取精确的平移参量,没有深度信息它们也无法用于稳像;3)旋转是造成视频抖动的主要原因,平移带来的抖动相对于选择而言可以忽略.Hanning等人[111]使用加速度传感器和陀螺仪传感器,采用3D旋转畸变模型来进行运动估计,并使用扩展Kalman滤波器EKF进行运动平滑,实现视频稳像.Jia等人[112-113]基于流体优化法提出一种使用陀螺仪的稳像方案,针对已标定相机使用3D旋转运动模型,利用流形黎曼几何法来平滑视频帧的相机旋转矩阵,将运动平滑规划为基于测地距的非线性流形约束回归问题.为解决构建的流形约束平滑问题,方案使用黎曼几何计算目标函数的梯度和海森矩阵,并且将欧氏空间中的二度量映射算法扩展到非线性流形结构中,以提高解决流形优化问题的效率.作为Karpenko等人[110]工作的续篇,Bell等人[114]针对定焦已标定相机,采用投影相机模型,借助陀螺仪传感器完成相机3D旋转抖动的稳像.文章提供一种非线性滤波方法,去掉所有小幅运动(不管其频率),对于大幅运动,采用平滑相机角速度的方法来输出平滑运动.另外一种方案,Sun[115]使用深度摄像头解决视频稳像问题,由于深度摄像头输出的深度信息有噪声、深度图像不完整且分辨率低,作者将深度图像与原图像结合来进行相机3D运动估计,即在2D特征点基础上使用深度信息完成相机3D运动估计并最终完成视频稳像.
这些使用传感器来辅助完成相机运动估计的方法的优点是减小了视频稳像算法的运算量,能够适用于计算能力相对较弱的智能设备.
2.3 本节小结
不同于传统技术的“黄金3步曲”,新兴稳像技术试图平衡效果和速度这一对矛盾,力求用接近传统2D方案的计算复杂度来达到近似传统3D方案的稳像效果.本节将新兴方案分为2类:新兴2D稳像技术和借助传感器稳像技术.新兴2D稳像将相机3D运动重建过程的约束条件放松,绕过复杂的3D重建操作,从特征轨迹和几何约束条件2个方面寻找新的稳像方案;借助传感器稳像方案将运动估计过程由传统图像处理方法转化为更加简单高效的硬件方法,极大提高运动估计速度,简化稳像过程.
3 总结与展望
3.1 总 结
本文对数字视频稳像技术进行了调研和综述.数字稳像技术发展的近40年间,从最初简单2D稳像技术发展到3D稳像,再发展到新兴2D稳像技术以及借助传感器稳像技术.
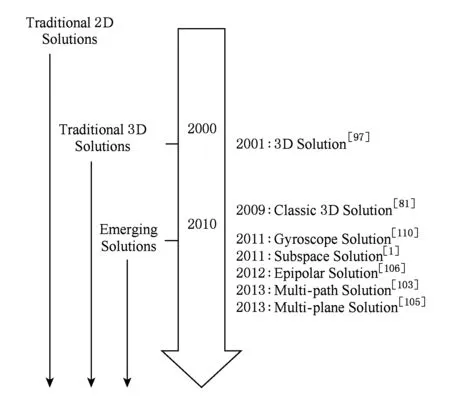
Fig. 4 Development of DVS techniques图4 数字视频稳像技术发展
最初简单2D稳像技术流行,一方面是因为当时视频设备的计算能力较弱,另一方面是因为当时视频质量较差,2D稳像可以达到应用需求.随着稳像技术的深入研究、视频设备计算体能的提高以及特征匹配问题的精确解决等一系列因素的驱动,3D稳像技术逐渐发展成熟并得以应用.近几年,随着智能终端设备占据主流市场,智能传感器的使用越来越普及,以及人们对于应用时效性的要求越来越高,研究者开始研究寻找更高效同时稳像效果接近3D稳像技术的方案,并取得了不错的成果,新兴2D稳像技术和借助传感器的稳像技术涌现出来,并突破了传统稳像技术的固定框架.这些技术的共同特点是用更简单的计算量达到接近3D稳像的效果.本文对数字视频稳像技术发展的总结如图4所示:
3.2 展 望
通过对数字视频稳像技术发展的总结分析,本文展望数字视频技术发展趋势和挑战热点为:
1) 视觉处理与传感器深入融合
即传统图像处理法与传感器的深入融合.在机器视觉和机器人应用中,视觉处理和传感器融合的方法应用较成熟.但在视频稳像应用中,鉴于设备计算能力和成本问题,二者融合的方案还并不多见.如何有效利用智能终端设备中的传感器资源,使之与图像处理算法更加高效地融合,会成为将来视频稳像技术的一个研究点.
2) 新型传感器的出现
陀螺仪等角速度传感器在视频稳像中的应用很多,而且效果不错.然而正如一些研究者在其研究成果的不足之处所提到的,借助传感器的方案都将运动模型选择为旋转模型,而忽略了平移对视频抖动的影响.理由是视频抖动主要由选择运动造成,因为一般情况下场景离相机较远.在智能终端设备普及的当前时代,室内或其他近距离视频应用场景越来越多,此时平移运动造成的抖动并不能简单忽略.另一方面,从学术研究角度看,完整的3D稳像研究也是必要的.当前加速度传感器无法直接用于精度要求较高的视频稳像应用,如果有精度更高的新型传感器出现,能够满足视频稳像的精度要求,则平移估计问题就迎刃而解.
3) 实时运动补偿的研究
不管是传统技术还是新兴技术,都涉及到运动补偿的问题,它的处理速度制约着视频稳像的处理速度.目前运动补偿常用的是Gaussian滤波器以及Kalman滤波器.Gaussian滤波器平滑效果很好,但适用于线下处理,即需要知道更多的运动状态(包括过去的和将来的);Kalman滤波器能够预测将来状态,但没有Gassian平滑效果好.如今智能终端设备对于应用的实时要求越来越高,例如实时视频聊天,急需更高效的实时运动平滑滤波器.
[1]Liu Feng, Gleicher M, Wang Jue, et al. Subspace video stabilization[J]. ACM Trans on Graphics, 2011, 30(1): 623-636
[2]Rawat P, Singhai J. Review of motion estimation and video stabilization techniques for hand held mobile video[J]. International Journal of Signal & Image Processing, 2011, 2(2): 159-168
[3]Ko S J, Lee S H, Lee K H. Digital image stabilizing algorithms based on bit-plane matching[J]. IEEE Trans on Consumer Electronics, 1998, 44(3): 617-622
[4]Morimoto C, Chellappa R. Automatic digital image stabilization[COL]Proc of IEEE Int Conf on Pattern Recognition. Piscataway, NJ: IEEE, 1996 [2016-02-19]. https:www.researchgate.netpublication247372692_Automatic_Digital_Image_Stabilization
[5]Irani M, Rousso B, Peleg S. Recovery of ego-motion using image stabilization[C]Proc of Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 1994: 454-460
[6]Chen Ting. Video stabilization algorithm using a block-based parametric motion model, EE392J[R]. Palo Alto, CA: Stanford University, 2000
[7]Bhaskar H, Bez H E. A novel block motion estimation model for video stabilization applications[C]Proc of Int Conf on Informatics in Control, Automation and Robotics. Piscataway, NJ: IEEE, 2007: 303-306
[8]Vella F, Castorina A, Mancuso M, et al. Digital image stabilization by adaptive block motion vectors filtering[J]. IEEE Trans on Consumer Electronics, 2002, 48(3): 796-801
[9]Vella F, Castorina A, Mancuso M, et al. A robust digital image stabilization algorithm using block motion vectors[C]Proc of Int Conf on Consumer Electronics. Piscataway, NJ: IEEE, 2002: 234-235
[10]Yang S H, Jheng F M. An adaptive image stabilization technique[C]Proc of IEEE Int Conf on Systems, Man and Cybernetics. Piscataway, NJ: IEEE, 2006: 1968-1973
[11]Battiato S, Puglisi G, Bruna A R. A robust video stabilization system by adaptive motion vectors filtering[C]Proc of ICME. Piscataway, NJ: IEEE, 2008: 373-376
[12]Chen Homer H, Liang Chiakai, Peng Yuchun, et al. Integration of digital stabilizer with video codec for digital video cameras[J]. IEEE Trans on Circuits & Systems for Video Technology, 2007, 17(7): 801-813
[13]Puglisi G, Battiato S. A Robust image alignment algorithm for video stabilization purposes[J]. IEEE Trans on Circuits & Systems for Video Technology, 2011, 21(10): 1390-1400
[14]Tang Chongwu, Yang Xiaokang, Chen Li, et al. A fast video stabilization algorithm based on block matching and edge completion[C]Proc of the 13th IEEE Int Workshop on Multimedia Signal Processing. Piscataway, NJ: IEEE, 2011: 1-5
[15]Foroosh H, Zerubia J, Berthod M. Extension of phase correlation to subpixel registration[J]. IEEE Trans on Image Processing, 2002, 11(3): 188-200
[16]Li Min, Biswas M, Kumar S. DCT-based phase correlation motion estimation[C]Proc of Int Conf on Image Processing. Piscataway, NJ: IEEE, 2004: 445-448
[17]Kumar S, Biswas M, Nguyen T. Efficient phase correlation motion estimation using approximate normalization[C]Proc of the 38th Asilomar Conf on Signals Systems and Computers. Piscataway, NJ: IEEE, 2004: 1727-1730
[18]Bi Lingyan, Chan Kowkping, Yu Yinglin. Modified CLT-domain motion estimation based on phase correlation[J]. Journal of Electronics, 2004, 21(2): 110-115
[19]Argyriou V, Vlachos T. A study of sub-pixel motion estimation using phase correlation[C]Proc of the British Machine Vision Conf. Durham, UK: BMVA, 2006: 387-396
[20]Ahmed J, Jafri M N. Improved phase correlation matching[G]Image and Signal Processing. Berlin: Springer, 2008: 128-135
[21]Yan Hongshi, Liu Jianguo. Robust phase correllation based motion estimation and its applications[C]Proc of the British Machine Vision Conf. Durham, UK: BMVA, 2008: 1045-1054
[22]Vera E, Torres S. Subpixel accuracy analysis of phase correlation registration methods applied to aliased imagery[C]Proc of the 16th European Signal Processing Conf. Piscataway, NJ: IEEE, 2008: 1-5
[23]Liu Yangke, De Jifu, Li Bo, et al. Real-time global motion vectors estimation based on phase correlation and gray projection algorithm[C]Proc of the 2nd Int Congress on Image and Signal Processing. Piscataway, NJ: IEEE, 2009: 1-5
[24]Chen Yueting, Wu Jiagu, Li Qi, et al. A windowed phase correlation algorithm for subpixel motion estimation[G]SPIE 7850: Proc of Int Society for Optical Engineering. Bellingham, WA: SPIE, 2010: 2280-2283
[25]Lai Lijun, Xu Zhiyong. Global motion estimation based on Fourier Mellin and phase correlation[C]Proc of the 2nd Int Conf on Civil, Materials and Environmental Sciences. Paris: Atlantis, 2015: 636-639
[26]Erturk S. Digital image stabilization with sub-image phase correlation based global motion estimation[J]. IEEE Trans on Consumer Electronics, 2003, 49(4): 1320-1325
[27]Erturk S. Translation, rotation and scale stabilization of image sequences[J]. Electronics Letters, 2003, 39(17): 1245-1246
[28]Sanjeev K, Haleh A, Mainak B, et al. Real-time affine global motion estimation using phase correlation and its application for digital image stabilization[J]. IEEE Trans on Image Processing, 2011, 20(12): 3406-3418
[29]Jia Ruiming, Zhang Hong, Wang Lei, et al. Digital image stabilization based on phase correlation[C]Proc of IEEE Int Conf on Artificial Intelligence and Computational Intelligence. Piscataway, NJ: IEEE, 2009: 485-489
[30]Zhang Yuefei, Xie Mei, Tang Dongming. A central sub-image based global motion estimation method for in-car video stabilization[C]Proc of the 3rd IEEE Int Conf on Knowledge Discovery and Data Mining. Piscataway, NJ: IEEE, 2010: 204-207
[31]Arnheim R. The perception of the visual world[J]. Journal of Aesthetics & Art Criticism, 1952, 11(2): 231-235
[32]Barron J, Fleet D, Beauchemin S S. Performance of optical flow techniques[J]. International Journal of Computer Vision, 1994, 12(1): 236-242
[33]Lucas B, Kanade T. An iterative image registration technique with an application to stereo vision[C]Proc of Int Joint Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 1981: 674-679
[34]Chang Hungchang, Lai Shanghong, Lu Kuangrong. A robust and efficient video stabilization algorithm[C]Proc of IEEE Int Conf on Multimedia and Expo. Piscataway, NJ: IEEE, 2004: 29-32
[35]Chang J Y, Hu Wenfeng, Cheng Muhuo, et al. Digital image translational and rotational motion stabilization using optical flow technique[J]. IEEE Trans on Consumer Electronics, 2002, 48(1): 108-115
[36]Cai Jinhai, Walker R A. Robust motion estimation for camcorders mounted in mobile platforms[C]Proc of Digital Image Computing: Techniques and Applications. Piscataway, NJ: IEEE, 2008: 491-497
[37]Bouguet J Y. Pyramidal implementation of the Lucas Kanade feature tracker description of the algorithm[R]. Santa Clara, CA: Intel Corporation Microprocessor Research Labs, 2000
[38]Cai Jinhai, Walker R. A Robust video stabilization algorithm using feature point selection and delta optical flow[J]. IET Computer Vision, 2010, 3(4): 176-188
[39]Harris C, Stephens M. A combined corner and edge detector[C]Proc of the 4th Alvey Vision Conf. Durham, UK: BMVA, 1988: 147-151
[40]Edward R, Reid P, Tom D. Faster and better: A machine learning approach to corner detection[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2010, 32(32): 105-119
[41]Shi Jiaobo, Tomasi C. Good features to track[C]Proc of IEEE Computer Society Conf on Computer Vision and Pattern Recognition. Los Alamitos, CA: IEEE Computer Society, 1994: 593-600
[42]Lowe D. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110
[43]Bay H, Tuytelaars T, Gool L V. SURF: Speeded up robust features[J]. Computer Vision & Image Understanding, 2006, 110(3): 404-417
[44]Amisha P. A survey on video stabilization techniques[J]. International Journal of Engineering Sciences & Research Technology, 2015, 4(2): 338-342
[45]Censi A, Fusiello A, Roberto V. Image stabilization by features tracking[C]Proc of IEEE Int Conf on Image Analysis and Processing. Piscataway, NJ: IEEE, 1999: 665
[46]Hu Rong, Shi Rongjie, Shen Ifan, et al. Video stabilization using scale-invariant features[C]Proc of the 17th IEEE Int Conf on Information Visualization. Piscataway, NJ: IEEE, 2007: 871-877
[47]Yang Junlan, Schonfeld D, Mohamed M. Robust video stabilization based on particle filter tracking of projected camera motion[J]. IEEE Trans on Circuits & Systems for Video Technology, 2009, 19(7): 945-954
[48]Shen Yao, Guturu P, Damarla T, et al. Video stabilization using principal component analysis and scale invariant feature transform in particle filter framework[J]. IEEE Trans on Consumer Electronics, 2009, 55(3): 1714-1721
[49]Pinto B, Anurenjan P R. SURF based robust video stabilization using Kalman filter[C]Proc of Int Conf on Technological Trends. Piscataway, NJ: IEEE, 2011 [2016-02-17]. https:www.researchgate.netpublication260384456_SURF_based_Robust_Video_Stabilization_Using_Klman_Filter
[50]Zhou Minqi, Asari V K. A fast video stabilization system based on speeded-up robust features[G]Advances in Visual Computing. Berlin: Springer, 2011: 428-435
[51]Zhang Kun, Xu Tingfa, Wang Ping, et al. Real-time full-frame digital image stabilization system by SURF[J]. Optics & Precision Engineering, 2011, 19(8): 1964-1972 (in Chinese)(张坤, 许廷发, 王平, 等. 高精度实时全帧频SURF电子稳像方法[J]. 光学精密工程, 2011, 19(8): 1964-1972)
[52]Zheng Xie, Cui Shaohui, Wang Gang, et al. Video stabilization system based on speeded-up robust features[C]Proc of Int Industrial Informatics and Computer Engineering Conf. Paris: Atlantis, 2015: 1995-1998
[53]Irani M, Anandan P. About direct methods[G]LNCS 1883: Vision Algorithms: Theory and Practice. Berlin: Springer, 1999: 267-277
[54]Torr P H S, Zisserman A. Feature based methods for structure and motion estimation[G]LNCS 1883: Vision Algorithms: Theory and Practice. Berlin: Springer, 1999: 278-294
[55]Kalman R E. A new approach to linear filtering and prediction problems[J]. Journal of Basic Engineering, 1960, 82(1): 35-45
[56]Valiviita S, Ovaska S J, Vainio O. Polynomial predictive filtering in control instrumentation: A review[J]. IEEE Trans on Industrial Electronics, 1999, 46(5): 876-888
[57]Erturk S. Image sequence stabilization: Motion vector integration (MVI) versus frame position smoothing(FPS)[C]Proc of the 2nd Int Symp on Image and Signal Processing and Analysis. Piscataway, NJ: IEEE, 2001: 266-271
[58]Jahne B B. Digital Image Processing: Concepts, Algorithms and Scientific Applications[M]. Berlin: Springer, 1992
[59]Yasuyuki M, Eyal O, Ge Weina, et al. Full-frame video stabilization with motion inpainting.[J]. IEEE Trans on Pattern Analysis & Machine Intelligence, 2006, 28(7): 1150-1163
[60]Xu Jie, Chang Huawen, Yang Shuo, et al. Fast feature-based video stabilization without accumulative global motion estimation[J]. IEEE Trans on Consumer Electronics, 2012, 58(3): 993-999
[61]Erturk S. Real-time digital image stabilization using Kalman filters[J]. Real-Time Imaging, 2002, 8(4): 317-328
[62]Litvin A, Konrad J, Karl W C. Probabilistic video stabilization using Kalman filtering and mosaicking[G]SPIE 5022: The Int Society for Optical Engineering. Bellingham, WA: SPIE, 2003: 663-674
[63]Gullu M K, Yaman E, Erturk S. Image sequence stabilisation using fuzzy adaptive Kalman filtering[J]. Electronics Letters, 2003, 39(5): 429-431
[64]Wang Dechong, Liang Aimin. Constraint translational and rotational motion filtering for video stabilization[C]Proc of the 13th European Signal Processing Conf. Piscataway, NJ: IEEE, 2005, 2005: 64-70
[65]Gordon N, Arulampalam M, Maskell S, et al. A tutorial on particle filters for online nonlinearnon-Gaussian Bayesian tracking[J]. IEEE Trans on Signal Process, 2002, 50(2): 174-188
[66]Yang Junlan, Schonfeld D, Chen Chong, et al. Online video stabilization based on particle filters[C]Proc of Int Conf on Image Processing. Piscataway, NJ: IEEE, 2006: 1545-1548
[67]Yang Junlan, Schonfeld D, Mohamed M. Robust video stabilization based on particle filter tracking of projected camera motion[J]. IEEE Trans on Circuits & Systems for Video Technology, 2009, 19(7): 945-954
[68]Chen Bingyu, Lee Kenyi, Huang Weiting, et al. Capturing intention-based full-frame video stabilization[J]. Computer Graphics Forum, 2008, 27(7): 1805-1814
[69]Zhang Fanglue, Wang Jue, Zhao Han, et al. Simultaneous camera path optimization and distraction removal for improving amateur video[J]. IEEE Trans on Image Processing, 2015, 24(12): 5982-5994
[70]Yoo S, Katsaggelos A K, Jo G, et al. Video completion using block matching for video stabilization[C]Proc of the 18th IEEE Int Symp on Consumer Electronics. Piscataway, NJ: IEEE, 2014: 1-2
[71]Hartley R, Zisserman A. Multiple View Geometry in Computer Vision[M]. 2nd ed. Cambridge, UK: Cambridge University Press, 2003
[72]Hartley R. In defense of the eight-point algorithm[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 1997, 19(6): 580-593
[73]Stewenius H, Nister D, Kahl F, et al. A minimal solution for relative pose with unknown focal length[C]Proc of IEEE Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2005: 789-794
[74]Kukelova Z, Bujnak M, Pajdla T. Polynomial eigenvalue solutions to minimal problems in computer vision[J]. IEEE Trans on Software Engineering, 2012, 34(7): 1381-1393
[75]Nister D. An efficient solution to the five-point relative pose problem[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2004, 26(6): 756-770
[76]Li Hongdong, Hartley R. Five-point motion estimation made easy[C]Proc of the 18th Int Conf on Pattern Recognition. Piscataway, NJ: IEEE, 2006: 630-633
[77]Brückner M, Bajramovic F, Denzler J. Experimental evaluation of relative pose estimation algorithms[C]Proc of the 3rd Int Conf on Computer Vision Theory and Applications. Piscataway, NJ: IEEE, 2008: 431-438
[78]Wang Jungming, Chou Hanping, Chen Seiwang, et al. Video stabilization for a hand-held camera based on 3D motion model[C]Proc of the 16th IEEE Int Conf on Image Processing. Piscataway, NJ: IEEE, 2009: 3477-3480
[79]van Wyk M A, Durrani T S, van Wyj B J. A RKHS interpolator-based graph matching algorithm[J]. IEEE Trans on Pattern Analysis & Machine Intelligence, 2002, 24(7): 988-995
[80]Zhang Guofeng, Hua Wei, Qin Xueying, et al. Video stabilization based on a 3D perspective camera model[J]. Visual Computer, 2009, 25(11): 997-1008
[81]Liu Feng, Gleicher M, Jin Hailin, et al. Content-preserving warps for 3D video stabilization[J]. ACM Trans on Graphics, 2009, 28(3): 341-352
[82]Lee T H, Lee Y G, Song B C. Fast 3D video stabilization using ROI-based warping[J]. Journal of Visual Communication & Image Representation, 2014, 25(5): 943-950
[83]Ryu Y G, Roh H C, Chung M J. 3D video stabilization for humanoid eyes using vision and inertial sensors inspired by human VOR[C]Proc of IEEE Int Conf on Robotics and Biomimetics. Piscataway, NJ: IEEE, 2010: 1780-1785
[84]Azuma R, Bishop G. Improving static and dynamic registration in an optical seethrough HMD[C]Proc of the 21st Annual Conf on Computer Graphics and Interactive Techniques. New York: ACM, 1994: 197-204
[85]Grassia F S. Practical parameterization of rotations using the exponential map[J]. The Journal of Graphics Tools, 1998, 3(3): 29-48
[86]Hanotaux G, Peroche B. Interactive control of interpolations for animation and modeling[COL]Proc of Graphics Interface. 1993: 201-208 [2016-02-19]. https:www.researchgate.netpublication243782403_Interactive_Control_of_Interpolations_for_Animation_and_Modeling
[87]Johnstone J K, Williams J P. Rational control of orientation for animation[COL]Proc of Graphics Interface. 1995: 179-186[2016-02-19]. https:www.researchgate.netpublication243781796_Rational_control_of_orientation_for_animation
[88]Shoemake K. Animating rotation with quaternion curves[J]. ACM SIGGRAPH Computer Graphics, 1985, 19(3): 245-254
[89]Hsieh C C, Fang Y C, Wang M E, et al. Noise smoothing for VR equipment in quaternions[J]. IIE Transactions, 1998, 30(7): 581-587
[90]Lee J, Shin S Y. Motion fairing[C]Proc of Computer Animation. Piscataway, NJ: IEEE, 1996: 136-143
[91]Lee J, Shin S Y. General construction of time-domain filters for orientation data[J]. IEEE Trans on Visualization and Computer Graphics, 2002, 8(2): 119-128
[92]Morimoto C, Chellappa R. Fast 3D stabilization and mosaic construction[C]Proc of IEEE Computer Society Conf on Computer Vision & Pattern Recognition. Piscataway, NJ: IEEE, 1997: 660-665
[93]Kang Singbing. Survey of image-based rendering techniques[G]SPIE 4067: The Int Society for Optical Engineering. Bellingham, WA: SPIE, 1997: 2-16
[94]Shade J, Gortler S, He Liwei, et al. Layered depth images[C]Proc of the 25th Annual Conf on Computer Graphics and Interactive Techniques. New York: ACM, 1998: 231-242
[95]Kang S B, Dinh H Q. Multi-layered image-based rendering[J]. Graphics Interface, 1999, 1(7): 2-13
[96]Buehler C, Bosse M, Mcmillan L, et al. Unstructured lumigraph rendering[C]Proc of Association for Computing Machinery. New York: ACM, 2001: 425-432
[97]Buehler C, Bosse M, Mcmillan L. Non-metric image-based rendering for video stabilization[C]Proc of the 2001 IEEE Computer Society Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2001: 609-614
[98]Wang Yushuen, Liu Feng, Hsu Pushen, et al. Spatially and temporally optimized video stabilization[J]. IEEE Trans on Visualization & Computer Graphics, 2013, 19(8): 1354-1361
[99]Lee Kenyi, Chuang Yungyu, Chen Bingyu, et al. Video stabilization using robust feature trajectories[C]Proc of IEEE Int Conf on Computer Vision. Piscataway, NJ: IEEE, 2009: 1397-1404
[100]Tomasi C, Kanade T. Shape and motion from image streams under orthography: A factorization method[J]. International Journal of Computer Vision, 1992, 9(2): 137-154
[101]Ryu Y G, Chung M J. Robust online digital image stabilization based on point-feature trajectory without accumulative global motion estimation[J]. IEEE Signal Processing Letters, 2012, 19(4): 223-226
[102]Ringaby E, Forssén P E. Efficient video rectification and stabilization for cell-phones[J]. International Journal of Computer Vision, 2012, 96(3): 335-352
[103]Liu Shuaicheng, Yuan Lu, Tan Ping, et al. Bundled camera paths for video stabilization[J]. ACM Trans on Graphics, 2013, 32(4): 96-96
[104]Bai J, Agarwala A, Agrawala M, et al. User-assisted video stabilization[C]Proc of the 25th Eurographics Symp on Rendering. New York: ACM, 2014: 61-70
[105]Wang Zhongqiang, Zhang Lei, Huang Hua. Multiplane video stabilization[C]Proc of Computer Graphics Forum. Hoboken, NJ: John Wiley & Sons, 2013: 265-273
[106]Goldstein A, Fattal R. Video stabilization using epipolar geometry[J]. ACM Trans on Graphics, 2012, 31(5): 573-587
[107]Laveau S, Faugeras O. 3-D scene representation as a collection of images[C]Proc of the 12th Int Conf on Pattern Recognition. Piscataway, NJ: IEEE, 1994: 689-691
[108]Hsu Yufeng, Chou Chengchuan, Shih Mingyu. Moving camera video stabilization using homography consistency[C]Proc of the 19th IEEE Int Conf on Image Processing. Piscataway, NJ: IEEE, 2012: 2761-2764
[109]Ryu Y G, Roh H C, Chung M J. Video stabilization for robot eye using IMU-aided feature tracker[C]Proc of IEEE Int Conf on Control Automation and Systems. Piscataway, NJ: IEEE, 2010: 1875-1878
[110]Karpenko A, Jacobs D, Baek J, et al. Digital video stabilization and rolling shutter correction using gyroscopes[R]. Palo Alto, CA: Stanford University, 2011
[111]Hanning G, Forslow N, Forssen P E, et al. Stabilizing cell phone video using inertial measurement sensors[C]Proc of IEEE Int Conf on Computer Vision Workshops. Piscataway, NJ: IEEE, 2011: 1-8
[112]Jia Chao, Evans B L. 3D rotational video stabilization using manifold optimization[C]Proc of Int Conf on Acoustics, Speech, and Signal Processing. Piscataway, NJ: IEEE, 2013: 2493-2497
[113]Jia Chao, Evans B L. Constrained 3D rotation smoothing via global manifold regression for video stabilization[J]. IEEE Trans on Signal Processing, 2014, 62(13): 3293-3304
[114]Bell S, Troccoli A, Pulli K. A non-linear filter for gyroscope-based video stabilization[C]Proc of European Conf on Computer Vision. Berlin: Springer, 2014: 294-308
[115]Sun Jian. Video stabilization with a depth camera[C]Proc of IEEE Computer Society Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2012: 89-95


Xie Wei, born in 1974. PhD. Professorate Senior Engineer. His main research interests include IC design and image processing.

He Zhiqiang, born in 1963. Professor, PhD supervisor. Member of CCF. His main research interests include computer architecture and computer application technology.
Digital Video Stabilization Techniques: A Survey
Wei Shanshan1,2, Xie Wei2, and He Zhiqiang3
1(SchoolofComputerScienceandEngineering,BeihangUniversity,Beijing100191)2(SoCCenter,LenovoCorporateResearch&Development,Beijing100085)3(Ecosystem&CloudServicesBusinessGroup,LenovoGroup,Beijing100085)
Digital video stabilization (DVS) techniques have been developing for over 30 years. The improvement of device computing ability, the research on related algorithms as well as the market needs have always been driving the development of DVS techniques: from simple solutions aimed at computing simplicity in early years to complex solutions aimed at stabilization effect, and further to advanced solutions trying to meet both computing simplicity and stabilization effect in recent years. In this survey, we first analyze the existing DVS techniques chronologically and then classify them into two basic catalogues: traditional techniques and emerging techniques. Traditional techniques are strictly based on typical motion models and rely on image processing algorithms for motion estimation. Emerging techniques relax the motion models and introduce novel techniques for motion estimation. According to the motion model they adopt, the traditional techniques are further divided into traditional 2D techniques and traditional 3D techniques. Similarly, the emerging techniques are further divided into emerging 2D techniques and sensor-based techniques. In each technique survey, we first analyze the key techniques it relies on and then list its applications in DVS. Finally, we summarize the existing DVS techniques and look into the challenges and developing trend of DVS techniques in the future.
digital video; stabilization; survey; traditional techniques; emerging techniques
his BSc and MSc degrees in computer science in North China Electric Power University in 2008 and 2011. Currently PhD candidate of computer science and technology in Beihang University. His main research interests include image processing and computer vision.
2016-02-19;
2016-12-09
TP391
