改进的BP神经网络在传动轴结构设计中的应用
2017-09-15杨宏才
王 胜,杨宏才
(西京学院 机电技术系,陕西 西安 710123)
改进的BP神经网络在传动轴结构设计中的应用
王 胜,杨宏才
(西京学院 机电技术系,陕西 西安 710123)
Shaffer函数定义域在[-10,10]区间内,BP神经网络拟合该函数训练时间长,且无法达到期望精度,说明BP神经网络拟合复杂非线性函数能力需改善。文章提出了一种改进的BP神经网络,先对网络的输入进行K-Means聚类,BP神经网络训练采用大规模节点,聚类输入分别激活部分节点进行训练,每组聚类使用不同的节点,通过子网络训练聚类样本,减少了网络拟合难度。经测试改进的BP神经网络达到了精度。最后,用改进的BP神经网络进行了轴径的最优计算。
BP神经网络;Shaffer函数;K-Means聚类;结构优化
1 人工神经网络研究背景
人工神经网络具有强大的函数拟合、数据预测、模式识别等能力,成为学术界的研究热点。BP神经网络是人工神经网络常见的一种形式,理论上已经证明,当BP神经网络的节点数足够大时,它可以拟合任意一种曲线[1],因而BP神经网络是使用最为广泛的一种网络。但BP神经网络存在一些问题,主要包括:训练时间过长;易陷入局部极小解;隐层节点数难以确定,隐层节点数太少,拟合精度达不到要求,隐层节点数太多,会导致计算负担过重。
学术界对BP神经网络主要的优化方向,一种是数值优化,主要有牛顿法、共轭梯度法;一种是启发式优化,常见的有动量算法、可变速率算法[2]。算法优化的另一个思路是多种算法的融合,粒子群神经网络[3],遗传神经网络[4],混沌神经网络[5],模拟退火神经网络[6],蚁群神经网络等[7],上述算法都在一定程度上改善了神经网路的性能,但是都无法完全克服BP神经网络的不足,特别是复杂非线性系统,网络的不足尤为明显。
针对BP神经网络上述不足,本文提出了一种改进的BP神经网络。用局部BP神经网络对部分样本进行训练,训练过的局部网络不再参与其他样本的训练,这些适应局部输入的网络综合成为大系统。该改进方法简化了目标,减少了网络负担。用Shaffer测试函数对网络性能进行了检测,达到了预设精度。将该网络应用于某型印刷机主传动轴轴径的计算,用该网络可以减少印刷机主传动轴设计的计算量。
2 BP神经网络算法概述
2.1 BP神经网络算法思想
BP神经网络主要由隐含层、输出层两层组成。BP神经网络运行包括两个过程,正向传播,输入数据自网络隐含层的权值、阈值、神经元函数处理后,传送到输出层;反向传播,当输出结果达不到期望精度时,由输出层到隐含层修正网络每一层神经元的权值和阈值。两个过程反复进行,最终使网络的性能函数达到要求。BP神经网络的具体算法参照文献[2]。
2.2 BP神经网络算法分析
本文采用Shaffer测试函数为例,对BP神经网络算法特点进行讨论,Shaffer函数如式(1)所示。
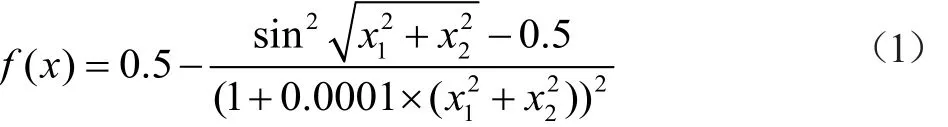
该函数是典型的非线性震荡函数,用BP神经网络对Shaffer函数进行拟合,随机产生10 000个训练样本,22个测试样本。神经网络的隐层采用sigmoid函数,隐层节点数设置为50,输出层采用purelin函数。训练步数设定为6 000,设定误差目标0.000 05。Shaffer函数的两个输入x1,x2定义域为[-10,10]时,用BP神经网络拟合,
网络训练用时3 284秒,训练很早就陷入了停滞,无法达到预设精度。可见,BP神经网络在应用时难以实现任意函数的拟合,需要隐层节点更加复杂的神经网络。但是神经网络结构的确定本身就是一个难点,且复杂的网络结构具有更大的训练负担。
2.3 BP神经网络的改进
本文提出一种BP神经网络的改进算法,具体做法是:
(1)对样本输入采用K-Means聚类法进行预处理,从S个样本中随机选取n个元素作为质心。计算其余元素到每个质心的欧式距离,将这些元素到质心距离最短的归为一类,分别为(S1,S2,...Sn),计算同类元素的平均值,作为新的质心μi,重复上述步骤直到质心收敛。距离计算表达式如式(2)所示。
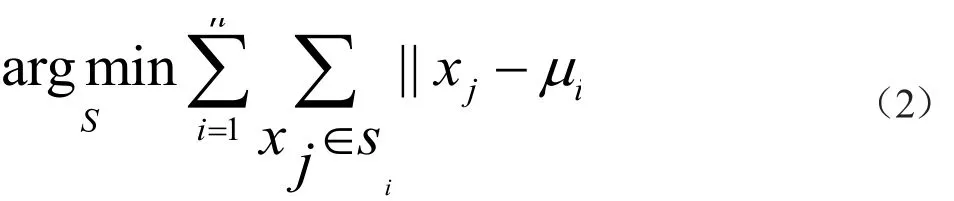
其中,xj是样本输入集合的一个元素,样本xj和质心μi均为多维。
(2)将聚类后的输入样本用改进的BP神经网络训练。网络的总节点数应满足n个聚类样本激活的节点的总和,聚类后的输入样本依次进入网络进行训练。每一聚类样本只激活部分节点参与训练,激活的最小节点数为网络输入数和输出数之和的5~10倍。新样本进入后,训练过的节点将不参与训练,激活新的节点继续训练。
(3)训练后的BP神经网络,实现了子网络对不同聚类的拟合。当有输入数据进入网络时,判断该数据属于何种聚类,通过网络对应激活的权值计算其输出。
2.4 改进的BP神经网络拟合Shaffer函数
采用改进的BP神经网络拟合Shaffer函数,网络最大节点数设置为500,每类样本初始激活15节点,随机产生10 000个输入样本,均匀随机选取9个质心进行K-Means聚类,聚类后的样本进入改进后的BP神经网络进行训练,经过362.223秒达到预设精度,用测试样本验证,其结果如表1所示。
经过测试样本进行验证,实际输出值与期望输出拟合较好,说明改进的BP神经网络拟合复杂的非线性函数具有良好的性能。
3 改进的BP神经网络的应用
某印刷厂拟对该型胶印机主传动轴进行技术改造。从节约材料、减轻重量、缩短响应时间等方面考虑,将原有的实心传动轴改造成空心传动轴。传动轴主要受到扭转力矩,应保证传动轴在最大扭转力矩作用下,具有足够的扭转强度和刚度。本文用改进的BP神经网络进行轴径设计。
3.1 轴径的设计分析
根据强度条件计算主轴的外径。主轴所受到的切应力应该小于主轴材料所允许的切应力。可得空心传动轴内外径比如式(3)所示。
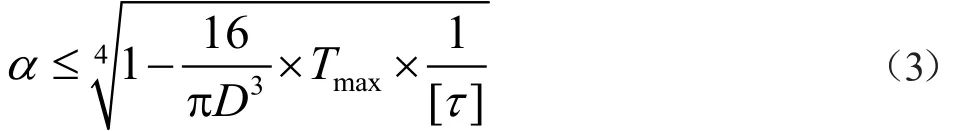
其中,Tmax为传动轴最大扭矩,单位kN·m,[τ]为轴的许用切应力,单位d为空心轴的内径,D为空心轴的外径,单位为m。
根据刚度条件计算主轴的外径如式(4)所示。

上式中,G为材料的切变模量,取值为79~81 GPa。[θ]为单位长度允许扭转角,单位°/m,取值0.15~1°/m。传动轴的内外直径比是一个典型的多输入单输出函数,其值受到轴的最大扭转力矩、轴的材料、外径、允许扭转角等因素影响,主轴设计力矩0.5~10 kN·m,许用直径0.02~0.120 m,轴类材料许用切应力如表2所示。
表中的每一个参数不一定都有可行解,且各个参数相互耦合,传统的BP神经网络难以完成公式(3)和(4)的拟合。本文用改进的BP神经网络拟合上述的计算公式。
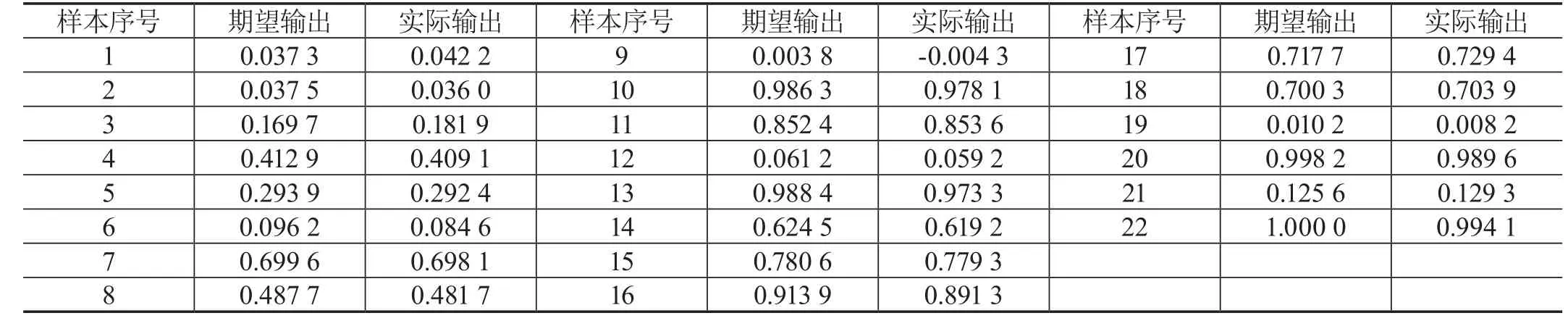
表1 改进的BP神经网络测试结果

表2 轴类材料设计参数
3.2 BP神经网络拟合内外径计算公式
用BP神经网络拟合强度条件下的公式(1),输入值分别为:轴外径、设计最大扭矩、许用切应力,输出为轴内外径比值。网络训练目标步数6 000,期望误差0.000 01,随机产生5 000个样本,其中的100个样本用作测试样本。由于3组输入值彼此差异过大,且量纲不一致,对输入样本线性归一化,如式(5)所示。

xnorm表示数据进行了线性化处理,该数据范围为[-1,1],没有量纲。对于样本中的非可行解,将该样本舍弃,可行解样本进入训练。
满足刚度条件下的公式(6)的拟合,输入值分别为轴外径、设计最大扭矩、允许扭转角,输出为轴内外径比值。其他网络参数以及拟合过程,与强度条件下的拟合类似,两个网络对可行解的拟合如图1所示。
改进的神经网络较好地完成了轴径公式的拟合任务,为轴的设计提供参考。轴径的最优解希望传动轴的直径、质量最小,承受的扭矩最大,设置最优解判定公式(6)。
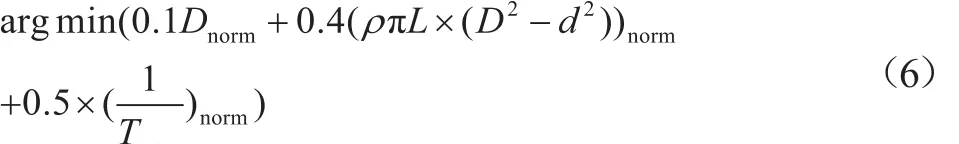

图1 改进的BP神经网络拟合轴计算公式
公式中的常数为权重系数,表明该项指标的重要性。为材料密度,单位:g/cm3。公式中轴直径、质量、扭矩的倒数均作归一化处理。用本文改进的BP神经网络拟合公式(6),训练样本为公式(3)和公式(4)的随机可行解。神经网络拟合结果如图2所示。
某型胶印机传动轴承受的最大扭矩Tmax为1.163 kN·m,安全系数为1.1~1.3,因此设计轴的扭矩1.2~1.5 kN·m。利用建立起的BP神经网络对轴径设计进行决策,有效解中40Cr等合金材料样本许用切应力为52 MPa,获得最优输出-0.608 8,外径D为0.062 7 m,内径d为0.050 7 m,内外径比值α为0.8080,最大扭矩Tmax为1.445 kN·m。
本文最后给出的设计建议是,采用40 Cr等合金材料,设计传动轴扭矩为1.445 kN·m时,传动轴轴外径D为0.060 0 m,内径d为0.050 0 m为最佳设计值。
4 结语
BP神经网络拟合Shaffer等非线性函数时,网络结构不易确定,训练时间长,且难以达到控制精度,本文提出了一种改进的BP神经网络,首先对样本输入进行K-Means聚类,BP神经网络产生一个大规模节点;每组聚类分别进入网络训练,训练时只激活部分节点,被激活的节点不再参与其他聚类的训练,即每一个节点只接受一种聚类。经过验证,改进的神经网络具有较快的收敛速度和良好的拟合精度,适用于拟合复杂的非线性函数,用改进的神经网络计算传动轴的轴径,并且拟合传动轴设计的最优决策,证明该算法具有良好的应用前景。
[1]HORNIK K,STINCHCOMBE M,WHITE H. Multilayer feedforward networks are universal approximators[J]. Neural Networks,1989(5):359-366.
[2]哈根.神经网络设计[M].戴葵,译.北京:机械工业出版社,2002.
[3]李松,刘力军,翟曼.改进粒子群算法优化BP神经网络的短时交通流预测[J].系统工程理论与实践,2012(9):2045-2049.
[4]徐小力,徐洪安,王少红.旋转机械的遗传算法优化神经网络预测模型[J].机械工程学报,2003(2):140-144.
[5]周颖,赵慧敏,陈阳,等.基于改进混沌自适应粒子群神经网络的磨矿粒度软测量[J].系统仿真学报,2016(12):2946-2950.
[6]尤丽华,吴静静,王瑶.基于模拟退火优化BP神经网络的pH值预测[J].传感技术学报,2014(12):1643-1648.
[7]孙旺,李彦明,杜文辽.基于蚁群神经网络的泵车主泵轴承性能评估[J].上海交通大学学报,2012(4):596-600.
[8]杨晓辉.简明机械实用手册[M].北京:科学出版社,2006.
Application of improved BP neural network in structural design of drive shaft
Wang Sheng, Yang Hongcai
(Mechanical and Electrical Engineering Department of Xijing University, Xi’an 710123, China)
The Shaffer function de fi nes the domain in the range of [-10,10], BP neural network fi tting function costs long training time, and can not achieve the desired accuracy, it showed that the ability of BP neural network to fi t the complicated nonlinear functions needs to be improved. This paper presents an improved BP neural network, fi rst, we should carry out K-Means clustering for the input of network, BP neural network is trained by large scale nodes, partial nodes are activated by clustering input to train, each cluster uses different nodes, by sub network to train clustering samples, it reduces network fi tting dif fi culty. The test results show that improved BP neural network meets the precision. Finally, the axle diameter is calculated optimally by the improved BP neural network.
BP neural network; Shaffer function; K-Means clustering; structure optimization
王胜(1982— ),男,陕西西安人。
