限定GA搜索空间的WSF求解算法①
2017-09-15蔡丽萍李世宝陈海华
蔡丽萍, 孙 莉, 李世宝, 陈海华, 龚 琛
(中国石油大学(华东)计算机与通信工程学院,青岛 266580)
限定GA搜索空间的WSF求解算法①
蔡丽萍, 孙 莉, 李世宝, 陈海华, 龚 琛
(中国石油大学(华东)计算机与通信工程学院,青岛 266580)
波达方向(DOA)估计在无线传感器网络中得到了广泛的应用,本文针对DOA中加权子空间拟合(WSF)算法多维非线性优化计算量大的问题,提出一种限定遗传搜索空间的WSF求解算法.该方法将旋转不变子空间(ESPRIT)与无偏估计量的理论最小误差(TME)相结合来限定遗传算法的搜索空间,通过缩短遗传算法的基因长度来降低加权子空间拟合算法的求解复杂度.仿真结果表明,该算法的估计性能与WSF基本相同,与其它的一些智能优化算法相比,显著的降低了算法的计算量.
波达方向估计;加权子空间拟合;遗传算法;计算复杂度;传感器网络
无线传感器网络(Wireless Sensor Network,WSN)是由传感、数据收集、处理和无线通信单元的低成本、小体积传感器节点构成的自组织网络,在特定的环境下自动的完成制定任务的智能系统.现在,无线传感器网络在医疗健康、生态环境监测、军事、智能交通控制等领域应用比较广泛[1,2].目标跟踪与定位成为当前无线传感器网络的热点问题.
近年来基于无线传感器网络目标定位的研究越来越多.比较常用的目标定位的方法主要有到达时间(Time of Arrival,TOA)、到达时间差[3](Time Delay of Arrival,TDOA)、波达方向估计[4](Direction of Arrival,DOA)等定位方法.其中DOA估计的基本理论和基本算法已经相当成熟,而且被广泛的应用在雷达、声纳、医学等许多的领域[5,6].基于子空间理论的加权子空间拟合(Weighted Subplace Fitting,WSF)算法[7]是DOA估计中的重要算法,该算法可以获得比较精确的信号方向估计值,但是此算法的计算复杂度比较高,在实际中难以使用,因此,如何降低WSF算法的计算量的问题已成为研究热点.
仿生学智能优化算法通过模拟自然界生物的行为来解决复杂的优化问题,随着优化算法的不断发展,这类优化算法被应用在对WSF算法的求解中.文献[8]入连续蚁群优化算法,通过利用算法中的信息量高斯概率分布函数求得全局最优值,减少了WSF算法的计算量;文献[9]利用人工蜂群优化算法对WSF算法中多维非线性问题进行优化,降低了WSF算法的计算复杂度;文献[10]采用混合蛙跳(Shuffled Frog Leaping Algorithm,SFLA)算法求解WSF算法,进而降低了WSF算法的运算时间;文献[11]在使用粒子群求解WSF算法的过程中,利用粒子群跟踪算法,将目标函数限定在一个很小的搜索空间内,减少了WSF算法的计复杂度.
遗传(Genetic Algorithm,GA)算法由于发展成熟、结构简单、全局搜索能力强等优点在许多复杂的优化问题中得到广泛的应用.文献[12]将GA算法应用在网络编码优化问题中,通过修正GA算法的流程使得优化算法的复杂度降低;文献[13]利用GA算法,对采用多变量、高非线性的似然函数的DOA估计进行求解,在保证全局收敛的同时降低了算法的复杂度;文献[14]将GA算法直接应用在对WSF算法的求解过程中,加快了WSF算法的收敛速度,减少了算法的计算量;文献[15]将模拟退火思想融合到GA算法中,改善传统GA算法的一些弊端,以降低WSF算法的计算复杂度.但是后前大多数是直接利用GA算法对WSF算法进行求解,缺少针对WSF算法的特性对GA算法中的参数进行修改,计算复杂度比较高.针对这一问题,本文在WSF算法的求解空间中利用ESPRIT算法结合无偏估计量的理论最小误差限定一个较小且包含全局最优值的搜索空间,在此较小的空间中利用GA算法进行求解,降低算法的计算复杂度.
1 数学模型
假设有q个远场窄带信号,入射到c个传感器上,入射角分别为其中传感器阵列之间的间距中心频率的波长则阵列输出表示为:


关于阵列快拍数据的协方差矩阵为:
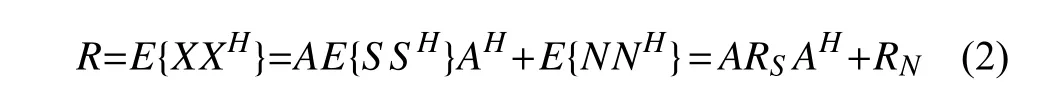
其中RS是信号协方差矩阵,RN是噪声协方差矩阵.在具体的实现中,对R进行特征值分解:

在理想情况下,当估计信源与真实信源相等时,可以得到:

当噪声存在时,上式(4)不一定成立.为解决上述问题,构造一个拟合关系,找出一个矩阵T使式(4)成立,且两者在最小二乘意义下拟合的最好,推广到一般形式的加权子空间拟合问题,即:

2 遗传算法
遗传算法具有很强的全局搜索性能,适合并行处理,在许多领域中得到了广泛的应用.图1是遗传算法的流程示意图.
它是利用“优胜劣汰,适者生存”的生物竞争进化理论,根据预先设定的目标适应度函数,通过遗传过程中的选择、交叉、变异对个体进行筛选,适应度高的个体得以保留,形成的新群体既继承上一代信息又优于上一代.通过不断的竞争选择,群体的适应值得到改善,使得种群朝着有最优解的方向进化,通过不断地繁衍进化,进而导群体逐渐逼近最优解,直到满足一定条件为止.

图1 遗传算法的流程示意图
3 限定遗传搜索空间的WSF求解算法
3.1 遗传算法搜索空间
3.1.1 定位搜索空间
旋转不变子空间(Estimation of signal parameters via rotational invariance techniques,ESPRIT)算法通过计算可以直接得到信号的方向信息,不存在谱峰搜索的步骤,计算复杂度远低于WSF算法,但是该算法的精度较低.因为ESPRIT算法和WSF算法都是对DOA估计求解,所以ESPRIT算法的解在WSF算法的全局最优解附近.因此,选用ESPRIT算法的解为中心缩小本文中遗传算法的搜索空间,加快算法收敛,进而降低算法的计算复杂度.
ESPRIT算法求解DOA是利用子阵间的旋转不变性,对于同一个信号的两个子阵X1、X2对应的阵列流型矩阵A1、A2之间存在一个旋转不变关系,由式(5)可以得知两个子信号的空间关系:

就能够获得信号的入射角信息.
3.1.2 确定基因长度
在本文中,通过对确定的合适搜索空间进行编码,进而确定GA算法的基因长度.
为了让GA算法更快地搜索出WSF算法的精确解,本文以ESPRIT算法的值为中心选取一个搜索空间.在保证一定精度的情况下,如果搜索空间选取的过大,此时GA算法需要选取初始种群中个体的种类较多,基因长度会变长,计算复杂度较高.如果搜索空间选取的太小可能不包含全局最优值,虽然GA算法选取的初始种群中个体的种类较少,基因长度会变短,算法需要执行到设定的遗传代数才可能停止计算,计算时间较长,复杂度升高.因此,一个合适的搜索空间对初始种群和基因长度的选取非常重要.
无偏估计量的理论最小误差(Theoretical Minimum Error,TME)可以为DOA无偏估计量的方差确定一个下界,TME的大小与SNR和快拍数有关.将放大μ倍的TME作为搜索空间的半边长,用来确定GA算法初始种群的基因长度.搜索空间的边长可以表示为2μ*TME.随着信号信噪比的降低,ESPRIT算法的均方误差会逐渐升高,与算法需要求得的全局最优值相差较大,但是搜索空间应该包含全局最优解,所以搜索空间的放大倍数μ也需要适当的增加,因此GA算法初始种群的基因长度需根据信噪比的变化进行调整.
初始化空间可表示为:

如果选取的搜索空间包含全局最优解且空间相对较小,此时GA算法的基因长度最合适,并且能够产生比较优良的初始种群个体,算法可以在较短的时间内搜索出全局最优值.
3.2 限定遗传搜索空间的WSF求解算法步骤
通过上文3.1节确定合适的搜索空间,在此确定空间的基础上通过入GA算法对WSF算法进行求解.
3.2.1 算法的步骤
限定GA搜索空间的WSF求解算法的设计步骤如下:
1)计算ESPRIT的解和TME.根据信噪比的不同确定TME的放大倍数,由式(12)划分出搜索空间的大小.
2)初始化种群.产生第一代个体,在经过1)步确定的搜索空间中,为了避免随机方式产生初始种群分布的不均匀,本文采用单元分布法,在搜索空间中根据种群的大小按照一定的单元选取种群的个体.

上式中θi是变量θ的第i个取值点.对取得的m个点采用十进制的编码方式产生初始种群.
3)适应值计算.选用上式(7)作为适应度函数,计算群体中个体的的适应值.
4)选择操作.选择父代种群个体要进行的操作.在实验中,采用最优值保存策略和比例选择法相结合,父代个体按适应度大小排序,然后根据最优保存策略,父代个体中适应值较高的个体替换适应值较低的个体,不进行5)步的操作直接遗传到子代.利用比例选择法选出父代中适应值较低的个体进行5)步操作.
5)交叉和变异操作.通过该操作增加种群的多样性.在实验中,分别采用的是单点交叉和基本位变异的方法.
6)迭代终止.若群体中个体的平均适应值趋于稳定或者达到设定的最大迭代次数,则停止迭代,输出算法的最优值;如果不满足终止条件,则返回第3)步继续进行迭代过程.
4 仿真性能分析
仿真模型:阵元数 M=16,阵元间距Δ=λ/2,其中λ是均匀线阵列接收信号的波长,信号的采样频率是1500 Hz,快拍数是100.本实验中遗传算法的参数的设置分别是:N=20,Pc=0.6,Pm=0.01.传统的遗传算法:N=100,Pc=0.6,Pm=0.01.有4个远场窄带信号源,入射角度分别是:-10°、15°、30°、45°.
为了证明本算法的有效性,在实验中将本文算法与其他常见的优化算法:传统的GA算法、MUSIC算法等进行算法性能上的比较.以下所有结果均为1000次实验下的平均值.
图2(a)、(b)分别是在4信源,SNR=-10 dB、0 dB和10 dB下,μ的取值对算法精度和算法时间的影响.从图中可以看出,当μ大于2时,μ的取值对算法的精度影响较小,此时搜索空间的大小包含全局最优值,随着μ取值的增加,GA算法初始种群中选取的个体种类较多,算法基因长度变长,计算复杂度较高.当μ小于2时,μ的取值对算法的影响较大,此时搜索空间的大小可能不包含全局最优值,虽然GA算法的初始种群中产生个体的种类较少,基因长度较短,但是算法执行到设定的次数也不一定找到全局最优值,计算复杂度较高.当μ等于2时,GA的搜索空间恰好包含全局最优值,GA算法的基因长度比较合适,此时算法复杂度较低.

图2 μ取值对算法的影响
图3(a)、(b)分别是在4个信源下,SNR从-10 dB~20 dB变化时,本文算法与WSF算法和MUSIC算法的计算精度在非相干和相干信号实验下的比较结果,从实验结果中可以看出,无论是相干还是非相干的情况,本文算法与WSF算法计算精度相当,当信噪比较低时,该算法的计算精度远远优于MUSIC算法.
表1是在SNR=0 dB、不同信源下,本文算法与传统GA算法、AM算法在保证精度相同时的计算时间.由表1可知,随着信号数量的增加,所有算法的计算时间都会升高.AM算法在求解最优值时是将一个多维问题转化成多个一维问题,随着信源数量的增加,计算时间呈指数增长.传统的GA算法的计算时间小于AM算法,但是计算复杂度仍然较高.本文算法有效的减小了GA算法的搜索空间,在计算过程中,减少了GA算法的基因长度和遗传代数,算法的计算复杂度更低.
图4是在4个信源的情况下,SNR从-10 dB~20 dB变化时,保证WSF算法的精度不变,本文算法与传统GA算法、AM算法的计算时间的对比,从图3可以看出,无论是相干信号(b)还是非相干信号(a),随着信噪比的增加,算法的计算时间在缓慢的减少,但是AM算法的计算时间远远大于其它两种算法,GA算法的计算时间虽然小于AM算法,但是仍大于本文算法.
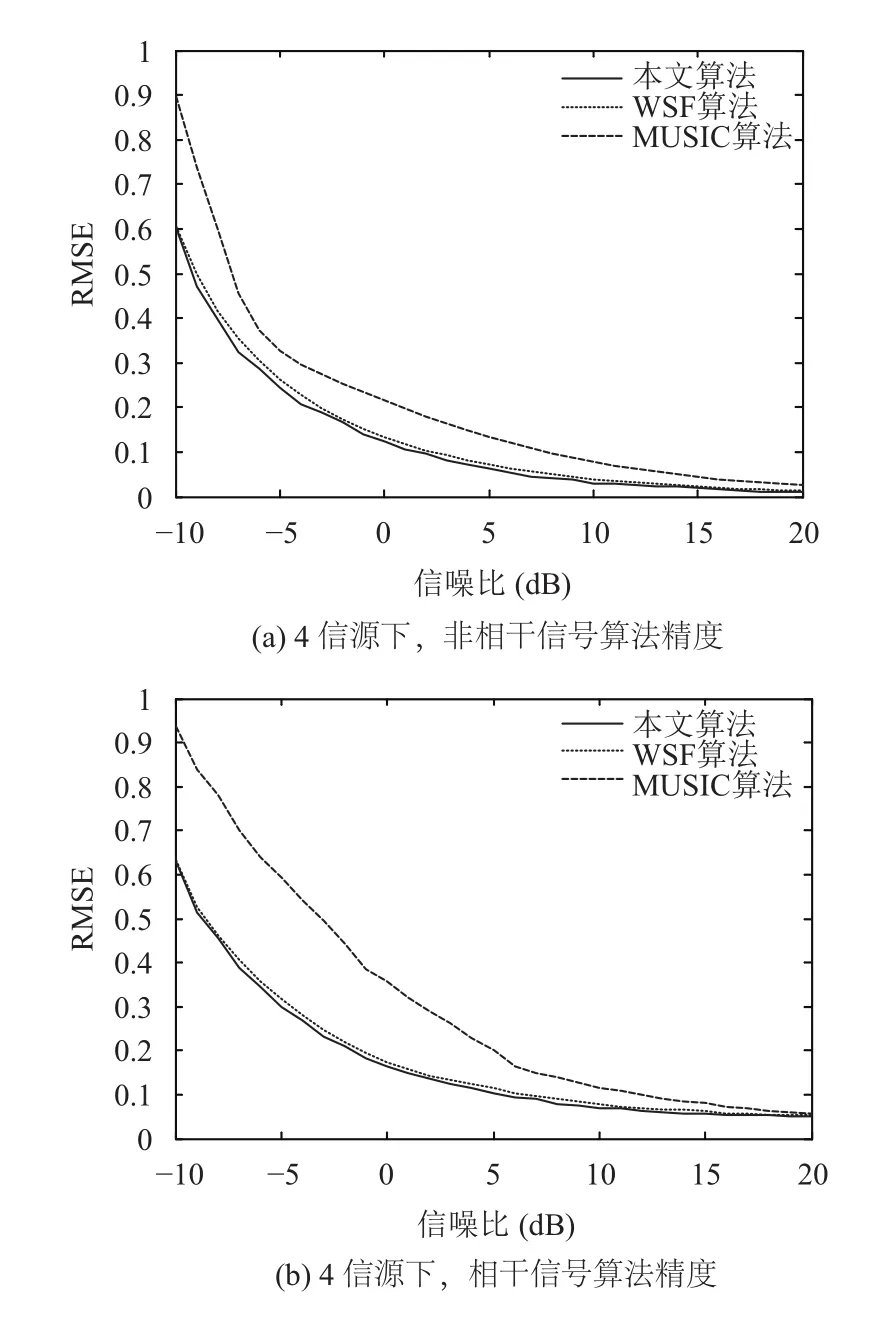
图3 4信源算法的估计精度

表1 不同信源算法的计算时间
5 结论
WSF算法的估计性能虽优于其它一些子空间分解类算法,但是由于该算法存在多维非线性搜索问题,计算量较大.本文针对WSF算法求解复杂度高的问题,利用ESPRIT算法和无偏估计量的理论最小误差确定GA算法搜索空间的位置和初始空间的大小,提出了一种限定GA搜索空间的加权子空间拟合算法.从仿真结果可以看出,本文算法在保证WSF算法的优良性能的同时,降低WSF算法的计算复杂度.尤其是在多信源的条件下,相比使用常规的GA算法直接求解,计算效率大幅度的提升.
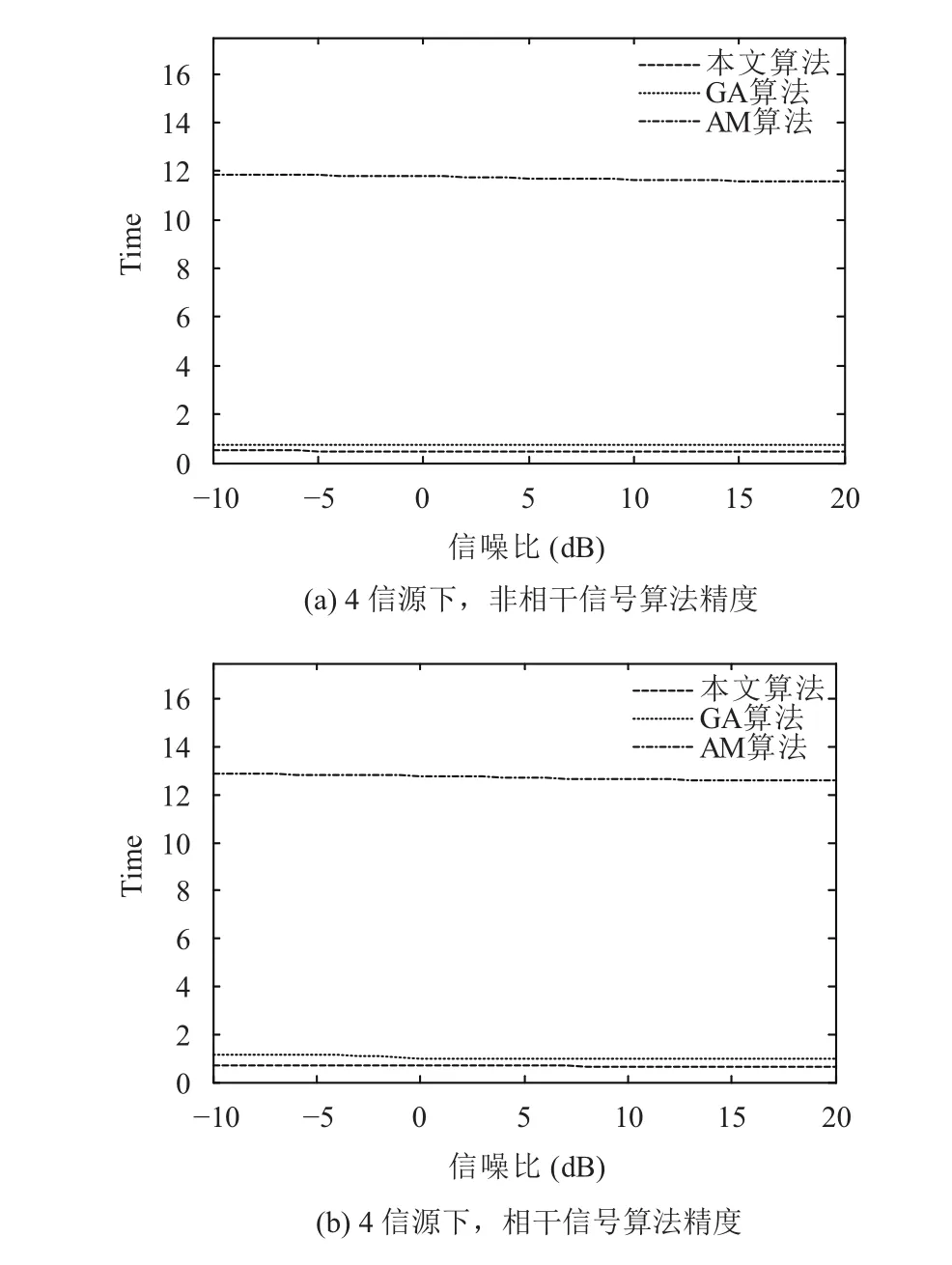
图4 4信源算法的计算时间
1 徐立锋.基于无线传感器网络技术在交通信息采集系统的应用.计算机应用与软件,2012,29(4):236–241,262.
2 王骥,林杰华,谢仕义.基于无线传感网络的环境监测系统.传感技术学报,2015,24(11):1732–1740.[doi:10.3969/j.issn.1004-1699.2015.11.026]
3 Yu Y,Silverman HF.An improved TDOA-based location estimation algorithm for large aperture microphone arrays.Proc.of IEEE International Conference on Acoustics,Speech,and Signal Processing,2004.Montreal,Que,Canada.2004,4.iv-77-iv-80.
4 Jian M,Kot AC,Er MH.DOA estimation of speech source with microphone arrays.Proc.of IEEE International Symposium on Circuits and Systems.Monterey,CA,Canada.1998.293–296.
5 黄中瑞,张剑云,周青松.双基地MIMO雷达发射功率聚焦的角度估计算法研究.电子与信息学报,2015,37(10):2314–2320.
6 Li YX,Gu SN,Zheng NE.MIMO radar transmit beampattern design for DOA estimation with sidelobe suppression.International Journal of Antennas and Propagation,2016,2016:1512843.
7 Viberg M,Ottersten B,Kailath T.Detection and estimation in sensor arrays using weighted subspace fitting.IEEE Trans.on Signal Proc.,1991,39(11):2436–2449.[doi:10.1109/78.97999]
8 焦亚萌,黄建国,韩晶.基于连续蚁群优化算法的小快拍加权子空间拟合快速算法.电子与信息学报,2011,33(4):972–976.
9 Zhang ZC,Lin J,Shi YW.Joint angle-frequency estimation based on WSF using artificial bee colony algorithm.Proc.of 2013 International Conference on Information Science and Technology (ICIST).Yangzhou,China.2013.1312–1315.
10 Zhang ZC,Yu XH,Sun HX.Weighted subspace fitting DOA estimation based on shuffled frog leaping algorithm.Applied Mechanics and Materials,2013,411-414:1049–1052.[doi:10.4028/www.scientific.net/AMM.411-414]
11 刁鸣,袁熹,高洪元,等.一种新的基于粒子群算法的DOA跟踪方法.系统工程与电子技术,2009,31(9):2046–2049.
12 邓亮,赵进,王新.基于遗传算法的网络编码优化.软件学报,2009,20(8):2269–2279.
13 Li M,Lu Y.Genetic algorithm based maximum likelihood DOA estimation.RADAR 2002.Edinburgh,UK.2002.502–506.
14 申冰,周群.一种基于遗传算法的加权子空间求解法.航天电子对抗,2007,23(3):51–53,60.
15 贾伟娜,刘顺兰.模拟退火遗传算法在DOA估计技术中的应用.计算机工程与应用,2014,50(12):266–270.[doi:10.3778/j.issn.1002-8331.1206-0247]
WSF Solving Algorithm Based on Limited GA Search Space
CAI Li-Ping,SUN Li,LI Shi-Bao,CHEN Hai-Hua,GONG Chen
(College of Computer and Communication Engineering,China University of Petroleum,Qingdao 266580,China)
The direction of arrival estimation has been widely employed in Wireless Sensor Networks.This paper proposes a Weighted Subspace Fitting algorithm which can largely reduce the computation amount when doing highdimensional non-linear optimization by limiting the genetic searching space.This method uses rotation invariant subspace and unbiased estimator of the theoretical minimum error to limit the search space and the complexity of WSF algorithm is reduced by shortening the genetic length of genetic algorithm.The simulation results show that this algorithm has the same performance as the WSF algorithm.Compared with other intelligent optimization algorithms,the proposed algorithm significantly reduces the computational complexity of the algorithm.
DOA estimation;weighted subspace fitting;genetic algorithm;computational complexity;wireless sensor networks
蔡丽萍,孙莉,李世宝,陈海华,龚琛.限定GA搜索空间的WSF求解算法.计算机系统应用,2017,26(9):170–175.http://www.c-sa.org.cn/1003-3254/5952.html
① 基金项后:中国自然科学基金青年基金(61601519);青岛市科技创新计划(2014-1-45);青岛市科技创新计划(15-9-80-jch);中央高校研究基金(15CX05025A)
2016-12-28;采用时间:2017-01-18
