基于用户信任和兴趣的概率矩阵分解推荐方法①

彭 鹏,米传民,肖 琳

(南京航空航天大学 经济与管理学院,南京 211100)

基于用户信任和兴趣的概率矩阵分解推荐方法①

彭 鹏,米传民,肖 琳

(南京航空航天大学 经济与管理学院,南京 211100)

传统协同过滤推荐算法存在数据稀疏性、冷启动、新用户等问题.随着社交网络和电子商务的迅猛发展,利用用户间的信任关系和用户兴趣提供个性化推荐成为研究的热点.本文提出一种结合用户信任和兴趣的概率矩阵分解(STUIPMF)推荐方法.该方法首先从用户评分角度挖掘用户间的隐性信任关系和潜在兴趣标签,然后利用概率矩阵分解模型对用户评分信息、用户信任关系、用户兴趣标签信息进行矩阵分解,进一步挖掘用户潜在特征,缓解数据稀疏性.在Epinions数据集上进行实验验证,结果表明,该方法能够在一定程度上提高推荐精度,缓解冷启动和新用户问题,同时具有较好的可扩展性.

推荐系统;协同过滤;社交信任;兴趣标签;概率矩阵分解

随着网络和信息技术的不断普及,人类产生的数据量正在呈指数级增长,“信息过载”(Information Overload)问题日益严重[1].作为帮助用户发现其感兴趣的物品、解决信息过载问题的重要工具,推荐系统应运而生.越来越多的电子商务服务商包括Amazon,Half.com,CDNOW,Netflix,和 Yahoo!等都致力于使用推荐系统为自身客户提供“量身定做”的购买建议[2].然而传统的协同过滤(Collaborative Filtering Recommendation,CF)推荐算法本身存在的数据稀疏性[3]、冷启动、新用户等问题,影响了推荐的精度与质量.

近年来,互联网用户数量呈现爆炸式增长,社交网络异军突起.2016年8月3日,中国互联网络信息中心(CNNIC)在京发布的第38次《中国互联网络发展状况统计报告》显示,截至2016年6月,中国网民规模达7.10亿,互联网普及率达到51.7%[4].美国著名的尼尔森调查机构调查了影响用户相信某个推荐的因素,调查显示,近百分之九十的用户相信朋友对他们的推荐[5].基于社交信任的推荐算法得到了广泛的研究,并且可以提高推荐的质量[6].然而,由于用户数后庞大,也存在用户间直接信任数据比较稀疏的问题.

在推荐系统中入用户信任关系能够缓解冷启动问题,加入用户兴趣能够缓解数据的稀疏性,基于以上事实,本文从用户评分角度挖掘用户间的隐性信任关系和潜在兴趣,在概率矩阵分解模型的基础上,融入用户信任关系信息、用户兴趣相似信息,提出一种新的结合用户信任和兴趣的协同过滤STUIPMF推荐方法(Recommended algorithm combined with social trust and user interest based on probability matrix factorization model).实验结果表明,本文所提出的方法能够在一定程度上提高推荐精度,同时缓解传统协同过滤推荐算法的冷启动和新用户等问题,具有较强的可扩展性.

1 相关工作

推荐算法(或叫推荐策略)是整个推荐系统中最为核心和关键的部分,在很大程度上决定了推荐系统性能的优劣[7].协同过滤推荐算法因其操作简单、解释性强、技术易于实现等优点成为应用最为广泛的推荐算法之一[8],其主要根据用户对项后的评分计算相似度的高低来进行推荐,但有研究表明,在大型电子商务系统上,用户评分项后一般不会超过项后总数的1%[9],因此其不可避免的会出现数据稀疏性、冷启动、新用户等问题.

为了解决这些问题,不少学者将信任机制入基于模型的协同过滤推荐算法,大致分为两类:一类是基于邻域模型研究信任关系的推荐方法:Massa提出Mole Trust模型,利用深度优先搜索评分用户,通过信任在用户A的社会网络边上的传递,预测其对目标用户 B的信任值[10];与之类似,Golbeck提出 Tidal Trust模型,改进宽度优先策略预测用户间的信任值[11];Jamali提出TrustWalker模型将基于项后的推荐系统与基于信任的推荐系统相结合[12].杨雪梅综合考虑用户评分相似性和用户之间信任关系,利用层次分析法构建用户信任模型,提出一种融合用户信任模型的协同过滤推荐算法[13].但是这些方法只考虑了近邻用户间的信任关系,忽视了对用户间的隐性信任关系的挖掘以及用户评分对推荐结果的影响.

另一类是基于矩阵分解模型考虑信任关系的推荐方法,Jamali提出融入用户信任信息的SocialMF(a matrix factorization based model for recommendation in social rating network)方法,入信任传播的概念,考虑直连的信任用户和二步连接的用户的信息来产生推荐,获得了较好的推荐效果,但计算复杂度较高,而且未采用不同的信任度量标准[14].Ma 等提出 SoRec(Social Recommendation)方法,通过共享用户隐特征向量空间把用户评分信息和用户社交信息联系起来进行研究[15].但这些方法更多是考虑直连的信任网络,而忽视了用户间隐性信任关系的挖掘.

由于基于矩阵分解的推荐算法利用的是隐因子,较难对推荐结果给出准确合理的解释.Salakhutdino等从概率的角度描述了矩阵分解问题,提出概率矩阵分解模型(Probabilistic Matrix Factorization,PMF),通过给用户-推荐项后的特征矩阵加上先验分布,并最大化预测评价的后验概率来进行推荐,并在Netflix数据集上得到了十分优秀的预测结果[16].Noam Koenigstein等人在概率矩阵分解过程中集成了部分物品特征信息,并且在Xbox电影推荐系统上进行实验,验证了所提模型的有效性[17].

有研究表明,考虑用户兴趣进行建模有利于做出更精准的个性化推荐.姚平平提出一种基于用户偏好和项后属性的协同过滤推荐算法,但忽视了用户间信任关系对于推荐结果的影响[18].Lee提出将用户偏好信息和社交网络中的信任传播相结合,提高推荐质量[19].陶俊等提出了一种适应用户兴趣多样性的基于用户兴趣分类的协同过滤算法并利用改进的模糊聚类算法,搜索最近邻来改善推荐算法的准确性[20].嵇晓声等提出了一种基于用户兴趣度的相似性度量方法,利用用户对不同项后类别的兴趣程度与用户评分相结合进行用户之间的相似性计算[21].但这些方法大多数都只关注用户对项后评分值,没有考虑用户偏好以及用户评分与项后属性之间的关系对推荐精度的影响,也忽视了用户间信任关系的挖掘.

因此,本文综合考虑用户对项后的评分和用户间的隐性信任关系,在概率矩阵分解模型基础上加入用户间的信任关系和用户兴趣信息,进一步挖掘出隐藏在信任关系和用户评分背后的用户特征,提出一种新的STUIPMF推荐算法,实验结果表明:该方法综合利用多方面信息,能够提升推荐精度和模型的可扩展性.

2 结合用户信任和兴趣的概率矩阵分解推荐算法

2.1 概率矩阵分解模型

概率矩阵分解模型的原理是从概率的角度来预测用户对项后的评分.为了便于形式化描述,本文将用到的参数符号,如表1所示.

表1 参数列表

PMF的计算过程如下:

假设用户和物品的隐式特征向量都服从高斯先验分布:

再假设已获取的用户评分数据的条件概率也服从高斯先验分布:

通过贝叶斯推理,可得用户和物品的隐式特征的后验概率:

这样,通过用户物品评分矩阵,就可以学习到用户和物品的隐特征向量,进而通过求内积的方式得到最近似的用户评分,用公式表示即:

图1 概率矩阵分解图模型

相应的概率图模型如图1所示.

2.2 挖掘用户隐性信任关系

基于信任的推荐算法可以有效解决推荐系统的冷启动和数据稀疏性问题,提高推荐覆盖率.本文通过研究发现,当前大多数算法只考虑直连的信任网络,即用户间的显性信任关系,而较少关注用户隐性信任关系的挖掘,所以入用户行为系数和用户信任度函数对用户信任关系衡量进行改进.

用户行为系数是基于用户评分信息进行信任推理,通过计算评分准确度得到,在用户评分相似度的基础上得到用户隐性信任关系;本文中,用户评分准确度利用用户与所有用户对项后平均评分的差值进行表示;一般来讲,用户评分的准确与否将直接影响其他用户对其信任的程度.表示用户u的用户行为系数,由用户评分准确度决定.

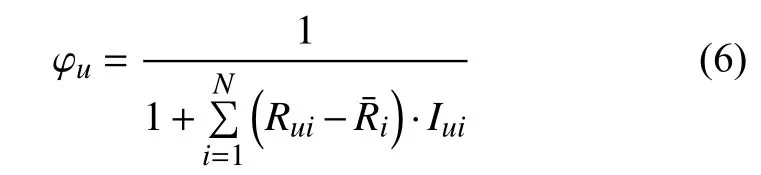
Rui表示用户u对项后i的评分,表示所有用户对于项后i的平均评分,如果用户u对项后i有评分,Iui=1,没有评分,则Iui=0.

评分相似度采用较为流行的Pearson相关系数进行度量.它首先需要找到用户i和用户j共同评分的项后集合,这个集合用表示,如此两个用户的相似性的计算公式为:

本文中用户隐性信任关系用TI表示,用户i和用户j的隐性信任关系:

本文用tij表示用户i和用户j的显式信任关系,用户 i信任用户 j时,tij=1,反之为 0.由于信任关系具有非对称性,tij并不能准确地反映用户之间的显性信任关系,还应跟信任和被信任的用户个数有关.比如,当用户ti信任很多用户时,用户ti和用户tj之间的信任值 tij应降低,反之,当用户 ti被很多用户信任时,用户ti和用户tj之间的信任值应得到增强.因此,结合用户影响力对用户之间的显性信任值进行改进:TEij表示改进后的显性信任值.

用户信任度函数用Tij表示,通过结合信任网络中声明的显性信任关系,确定显性信任和隐性信任各自的权重系数之后计算获得.

其中α代表权重系数.

用户信任关系矩阵用T表示,元素Til表示用户Ui与朋友Fl之间的信任度,已知用户信任条件概率分布函数,如下所示:

U和F概率分布,如下所示:

根据贝叶斯推理,如下所示:

基于用户信任关系的模型,相应的概率图模型如图2所示.

图2 基于用户信任关系的概率图模型

2.3 挖掘用户兴趣相似关系

本文研究发现当前基于用户兴趣分类的算法较少关注用户偏好以及用户评分与项后属性之间的关系对推荐结果精度的影响,所以本文基于用户—项后评分矩阵结合项后类型信息和用户评分阈值,挖掘用户隐性标签,得到用户—兴趣标签矩阵,进而补充用户信息,缓解数据稀疏性.

用户兴趣标签矩阵用P表示,元素Pik表示用户Ui在兴趣标签Lk上的标记次数,已知用户兴趣标签概率分布函数,如下所示:

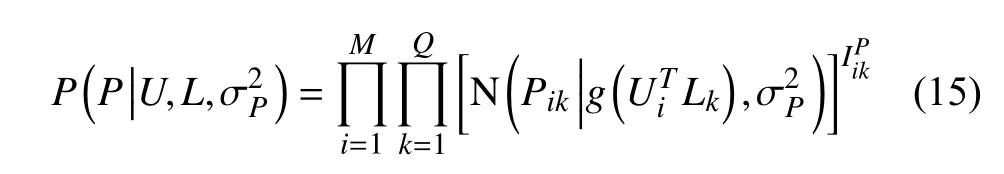
Ui和L的概率分布,如下所示:

根据贝叶斯推理,如下所示:

基于用户兴趣标签的模型,相应的概率图模型如图3所示.

图3 基于用户兴趣标签的概率图模型

3 融合用户信任和兴趣的STUIPMF模型具体实现

概率矩阵分解算法仅依据用户-项后评分矩阵,学习相应的特征向量,并没有考虑用户之间信任关系以及用户兴趣对推荐结果的影响,为了体现这一影响,本文对上述模型进行改进,将用户信任关系矩阵、用户兴趣标签矩阵和用户-项后评分矩阵的分解整合起来,通过用户潜在特征矩阵进行连接,提出STUIPMF模型,如图 4 所示.

联合之后的后验概率的对数值满足下式:

图4 STUIPMF 概率图模型

本文采用随机梯度下降法学习得到相应的潜在特征矩阵:

每次迭代时,Ui,Vj,Lk,Fl调整如下:

其中,γ为预先定义的步长.

重复上述训练过程,每次迭代后,计算并验证平均绝对误差,当目标函数S值的变化小于预先定义的很小的常数后终止迭代过程.得到迭代终止后的Ui,Vj,Lk,Fl之后,就可以预测用户Ui对商品Vj的未知评分,对于每一个用户,根据计算得到的预测评分值由高到低对候选商品进行排序,产生Top—N推荐列表,然后推荐给用户.

4 实验验证及结果分析

4.1 数据集介绍

Epinions作为1999年在美国成立的一个点评性质的网站,用户在上面能够浏览到其他用户对于琳琅满后的物品的评论,进而为其购物、选择公司、观看节后或者电影时提供参考意见.网站定位是“社会化商务”,它建立了一种“信任机制”,即用户能够对他人对物品点评质量的好坏做出自己的判定,假如相信某个用户,就可以把他加入自己的信任列表,反之也有权利加入不信任列表.这样Epinions网站的数据中就同时包含用户评分信息和用户信任关系,因此在当前推荐系统研究领域,都会把Epinions数据集作为一个基准数据库,来进行基于信任的推荐方法的研究.

本文的数据集就是由 Pao1o Massa 和 Paolo Ave sani提供的,爬取自“Epinions.com”的网站.关于这个数据集的统计情况如表2所示.

表2 Epinions 数据集的统计信息

4.2 评价指标

为了评价推荐系统预测的准确性,本文采用常用的评价指标:平均绝对误差(MAE,全称 Mean Absolute Error)和 RMSE 均方根误差(Root Mean Squared Error,RMSE),分别定义如下:

其中n为参与预测的项后数,pi是系统预测的目标用户的评分,ri是目标用户实际评分.

将本文所提算法与文献[16]提到的PMF模型、文献[14]提到的SocialMF模型、文献[15]提到的SoReg这三种典型推荐算法的效果进行对比.

4.3 参数λP、λF的影响

在本文所提的方法中,参数λP、λF的设置显得至关重要,它们起到平衡的作用.当λP设置为 0 时,系统推荐时就不考虑用户之间的信任关系,而只考虑用户的评分矩阵和用户的隐性兴趣标签.当λP设置为无穷大时,系统推荐时就只考虑用户之间的信任关系,而不考虑其他因素;同理,当λF设置为 0 时,系统推荐时就不考虑用户的隐性兴趣标签,而只考虑用户的评分矩阵和用户之间的信任关系.当λF设置为无穷大时,系统推荐时就只考虑用户隐性兴趣标签,而不考虑其他因素.

图5显示的是在其他参数设置不变的情况下,参数λP在潜在特征数分别为5和 10的情况下对MAE 和 RMSE 的影响.由图 5 的(a)和(b)可知,随着λP的增加,MAE和RMSE都在降低,即预测的准确性在提高;当λP达到一定阈值时,随着λP的增加,MAE和RMSE都在提高,即预测的准确性在降低.由此可得出,λP∈[0.01,0.1]时,推荐的准确度比较高,因此,在后面的实验中我们均采用这个区间的平均值作为近似最优值,即λP=λF=0.005 进行实验.图 6 展示的λF取值的影响,同理,在此不再赘述.

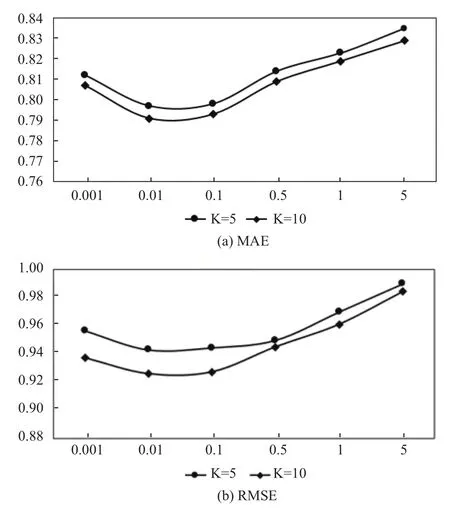
图5 参数λP对 MAE 和 RMSE 的影响

为了验证实验效果,分别选择其中80%的用户作为训练集,20%的用户作为测试集和90%的用户作为训练集,10%的用户作为测试集进行实验.

在实验过程中,相关参数主要是根据实验效果进行最优选择的.本文的STUIPMF推荐方法的参数设置如下:,λP=λF=0.005,特征向量K的取值分别为5和10;其他方法的参数设置:在PMF方法中,;在SocialMF方法中,;在 S o R e g 方 法 中,STUIPMF 方法与其他方法的试验效果对比如图7、图8所示.

图6 参数λF对 MAE 和 RMSE 的影响

图7 STUIPMF 方法与其他方法实验效果对比(80%训练集)

根据图7、8所示,我们可以得出如下结论:

1)本文所提出的STUIPMF模型综合考虑了用户评分信息、用户信任关系和兴趣信息,在所有实验参数都选择最优的情况下,80%作为训练集,20%作为测试集时,与 PMF、SocialMF、SoReg 相比,MAE 值分别下降17%、5.8%、5.3%,RMSE值分别下降21%、13%、4%;90% 训练集,10% 测试集时,与 PMF、SocialMF、SoReg相比,MAE值分别下降16.2%、4.1%、3.7%,RMSE值分别下降20.8%、13.5%、4.1%;说明本文所提方法在推荐准确性上有所提高.

2)随着隐特征向量维数的增加,推荐的精度有所提高,但另一方面可能出现过拟合和计算复杂度增加的问题.

3)对用户信任关系矩阵和用户兴趣标签矩阵进行概率矩阵分解后,能增加用户特征的先验信息,从而缓解推荐系统中的冷启动和新用户问题.

图8 STUIPMF方法与其他方法实验效果对比(90%训练集)

5 结论及展望

随着个性化服务在当今经济和社会生活中的地位和重要性日益突出,如何通过用户行为准确把握用户真实兴趣与需求,提供高质量的个性化推荐成为当前的研究热点.针对传统协同过滤方法存在的冷启动和数据稀疏性等问题,本文提出一种结合用户信任和兴趣的概率矩阵分解推荐方法(STUIPMF方法).首先从用户评分角度挖掘用户间的隐性信任关系和潜在兴趣标签,然后利用概率矩阵分解模型对用户评分信息、用户信任关系、用户兴趣标签信息进行矩阵分解,进一步挖掘用户潜在特征,缓解数据稀疏性,产生更精准的推荐.在Epinions数据集上进行实验验证,结果表明,本文所提出的STUIPMF方法综合利用用户评分、用户信任关系、用户兴趣等多方面信息,能够在一定程度上提高推荐精度,缓解冷启动和新用户问题,同时具有较强的可扩展性.

但其中也存在一些问题,比如模型中λ的取值我们是使用的是近似最优值,接下来将进一步确定λ的最优值以及动态λ值的变化,提高推荐准确度;另一方面会考虑更多的信息融入所提模型中,如文本信息、位置信息、时间因素等,关注用户信任关系和兴趣的更新,以及加入对用户之间不信任关系的考量.

1 Borchers A,Herlocker J,Konstan J,et al.Ganging up on information overload.Computer,1998,31(4):106–108.[doi:10.1109/2.666847]

2 Linden G,Smith B,York J.Amazon.com recommendations:Item-to-item collaborative filtering.IEEE Internet Computing,2003,7(1):76–80.[doi:10.1109/MIC.2003.1167344]

3 Vozalis E,Margaritis KG.Analysis of recommender systems’algorithms.Proc.of the the 6th Hellenic-European Conference on Computer Mathematics and its Applications.Athens,Greece.2003.732–745.

4 中国互联网络信息中心.第38次《中国互联网络发展状况统计报告》.北京:中国互联网络信息中心,2016.

5 Bobadilla J,Ortega F,Hernando A,et al.Recommender systems survey.Knowledge-Based Systems,2013,46:109–132.[doi:10.1016/j.knosys.2013.03.012]

6 Guo GB.Integrating trust and similarity to ameliorate the data sparsity and cold start for recommender systems.Proc.of the 7th ACM Conference on Recommender Systems.Hong Kong,China.2013.451–454.

7 王国霞,刘贺平.个性化推荐系统综述.计算机工程与应用,2012,48(7):66–76.

8 张学钱,林世平,郭昆.协同过滤推荐算法对比分析与优化应用.计算机系统应用,2015,24(5):100–105.

9 Sun XH,Kong FS,Ye S.A comparison of several algorithms for collaborative filtering in startup stage.Proc.of 2005 IEEE Networking,Sensing and Control.Tucson,AZ,USA.2005.25–28.

10 Massa P,Avesani P.Trust-aware recommender systems.Proc.of the 2007 ACM Conference on Recommender Systems.Minneapolis,MN,USA.2007.17–24.

11 Golbeck J.Personalizing applications through integration of inferred trust values in semantic web-based social networks.Proc.of Semantic Network Analysis Workshop.Galway,Ireland.2005.

12 Jamali M,Ester M.TrustWalker:A random walk model for combining trust-based and item-based recommendation.Proc.of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.Paris,France.2009.397–406.

13 杨秀梅,孙咏,王丹妮,等.融合用户信任模型的协同过滤推荐算法.计算机系统应用,2016,25(7):165–170.[doi:10.15888/j.cnki.csa.005229]

14 Jamali M,Ester M.A matrix factorization technique with trust propagation for recommendation in social networks.Proc.of the 4th ACM Conference on Recommender Systems.Barcelona,Spain.2010.135–142.

15 Ma H,Yang HX,Lyu MR,et al.SoRec:Social recommendation using probabilistic matrix factorization.Proc.of the 17th ACM Conference on Information and Knowledge Management.Napa Valley,California,USA.2008.931–940.

16 Salakhutdinov BR,Mnih A.Probabilistic matrix factorization.Proc.of the 20th International Conference on Neural Information Processing Systems.2015.1257–1264.

17 Koenigstein N,Paquet U.Xbox movies recommendations:Variational bayes matrix factorization with embedded feature selection.Proc.of the 7th ACM Conference on Recommender Systems.Hong Kong,China.2013.129–136.

18 姚平平,邹东升,牛宝君.基于用户偏好和项后属性的协同过滤推荐算法.计算机系统应用,2015,24(7):15–21.

19 Lee WP,Ma CY.Enhancing collaborative recommendation performance by combining user preference and trust-distrust propagation in social networks.Knowledge-Based Systems,2016,(106):125–134.[doi:10.1016/j.knosys.2016.05.037]

20 陶俊,张宁.基于用户兴趣分类的协同过滤推荐算法.计算机系统应用,2011,20(5):55–59.

21 嵇晓声,刘宴兵,罗来明.协同过滤中基于用户兴趣度的相似性度量方法.计算机应用,2010,30(10):2618–2620.

Recommended Algorithm Based on User Trust and Interest with Probability Matrix Factorization

PENG Peng,MI Chuan-Min,XIAO Lin
(College of Economics and Management,Nanjing University of Aeronautics and Astronautics,Nanjing 211100,China)

The traditional collaborative filtering recommendation algorithm has such problems as data sparseness,coldstart and new users.With the rapid development of social network and e-commerce,how to provide personalized recommendations based on the trust between users and user interest tag is becoming a hot research topic.In this study,we propose a probability matrix factorization model (STUIPMF)by integrating social trust and user interest.First,we excavate implicit trust relationship between users and potential interest label from the perspective of user rating.Then we use the probability matrix factorization model to conduct matrix decomposition of user ratings information,users trust relationship,user interest label information,and further excavate the user characteristics to ease data sparseness.Finally,we make experiments based on the Epinions dataset to verify the proposed method.The results show that the proposed method can to some extent improve the recommendation accuracy,ease cold-start and new user problems.Meanwhile,the proposed STUIPMF approach also has good scalability.

recommender system;collaborative filtering;social trust;interest tag;probability matrix factorization

彭鹏,米传民,肖琳.基于用户信任和兴趣的概率矩阵分解推荐方法.计算机系统应用,2017,26(9):1–9.http://www.c-s-a.org.cn/1003-3254/5933.html

①基金项后:江苏省高校哲学社会科学基金(2015SJD039);中央高校基本科研业务费专项资金(NS2016078)

2016-12-23;采用时间:2017-01-12