基于相似度的K阶临近定位算法①
2017-09-15马文丽李世宝张志刚杨喜鹏王升志
马文丽, 李世宝, 张志刚, 杨喜鹏, 王升志, 张 鑫
(中国石油大学(华东)计算机与通信工程学院,青岛 266580)
基于相似度的K阶临近定位算法①
马文丽, 李世宝, 张志刚, 杨喜鹏, 王升志, 张 鑫
(中国石油大学(华东)计算机与通信工程学院,青岛 266580)
基于WIFI位置指纹的定位系统能实现较高精度的室内定位,其中基于接收信号强度指示(RSSI)的近邻选择算法在进行室内定位时容易入奇异点,导致定位精度降低.针对该问题,本文提出了一种基于相似度的K阶临近定位算法(SKNN).该算法借鉴二部分网络中求解节点相似性的思想,建立位置指纹与AP之间的二部分网络,并提出一个相似度参数,用该参数去修正K阶临近定位算法.实验结果表明,本文提出的SKNN算法可以有效的降低奇异点对定位结果的影响,提高定位精度,80%的定位误差均在2 m以内,且在大场景中效果明显.
室内定位;位置指纹;近邻选择算法;二部分网络;相似度
1 相关研究
近邻选择算法[4]由于计算简单、易于实现而得到广泛应用,其核心在于通过计算欧氏距离寻找与待测点距离最近的一个或多个采样点.常见的近邻选择算法有最近邻法(Nearest Neighborhood,NN),K阶临近法(K-Nearest Neighborhood,KNN),加权K阶临近法(Weighted K-Nearest Neighborhood,WKNN),聚类过滤法(Cluster Filtered KNN,CFK)等.
NN算法是所有基于RSSI距离近邻选择算法中最简单的一种.将移动端采集到的RSSI向量与指纹数据库中所有指纹点进行匹配,计算欧氏距离Dist,距离最小的点对应的位置信息(xi,yi)即为对待测点的位置估计.RADAR系统[5]使用NN算法进行指纹的匹配与计算,实现了2~5米的定位精度.KNN算法[6]是对NN算法的改进,用NN算法中计算距离的方法计算得到具有最小距离的个指纹点(xi,yi),i∈(1,K),那么待测点的位置估计就是这K个指纹点位置的质心有效解决偶然性导致较大定位误差的问题.为了提高了定位精度,文献[7]提出WKNN算法,在选出K个相近的指纹后,不是直接计算K个点的质心,而是先根据每个指纹点的RSSI值计算它对待测点的贡献度,将贡献度作为权值分配给各个指纹点,然后求K个指纹点的加权质心,质心的位置即为最终的位置估计,能有效提高定位精度.由于指纹数据库中存在RSSI向量相似但实际位置相距较远的指纹点,将与待测点的RSSI向量值相似但实际位置相距较远的指纹点称为奇异点,上述近邻选择算法在进行指纹匹配时容易入奇异点,从而导致定位精度降低.
文献[8]针对指纹数据库中奇异点,在求解信号欧氏距离时进行加权处理.Jun MA等人提出聚类过滤KNN算法[9],该算法针对利用聚类算法滤除奇异点.王跃等人提出一种基于模拟退火聚类的室内定位算法[10].该算法采用模拟退火聚类的方法消除了具有一定特征相似性的奇异点.文献[11]提出采用模糊K-均值聚类的方法对KNN方法进行改进,利用K-均值聚类奇异点进行筛选.
通过聚类算法滤除奇异点的方法时间开销是非常大的,在具体应用上不能满足用户对实时性的要求.聚类算法也不能保证达到最优的聚类效果,两种采用K-均值聚类的算法在聚类的时结果受初始值的影响大,并且容易出现局部最值的问题.虽然一定程度上减小了奇异点的影响,但并没有提高匹配定位的效率.针对上述问题,本文借鉴二部分网络中判断节点之间相似度的思想,将指纹点和AP建成二部分网络,考虑指纹点之间共同连接的AP数后对定位的影响,提出基于相似度的KNN算法(Similarity-beased K-Nearest Neighborhood,SKNN).
2 SKNN算法
针对奇异点影响近邻选择算法定位精度的问题,本文对原有的阶临近定位算法进行改进,提出了SKNN算法.在算法设计过程中,需要解决的难点问题是分析奇异点影响定位精度的根本原因、建立指纹点和AP的二部分网络和相似度的计算.针对以上问题,将该算法的设计分为以下四个步骤:网络的建立、相似度的计算、基于相似度的加权欧氏距离计算和真实位置估计.算法流程图如图1所示.
2.1 网络的建立
鉴于上述思想,本文将指纹匹配的问题用二部分网络中求解节点相似性的思想解决,首先将指纹数据库中的每个指纹点位置作为X集合,AP点的集合作为Y集合,指纹点Xi中收到APj的信号即为Xi与Yj之间产生一条连边Eij,将实际网络表示成二部分网络,如图3,用不同指纹点之间共同连接的AP的数后来衡量两个指纹点之间的相似性.本文入一个“邻居”的概念:在“AP-指纹”网络中,与指纹点有连边的AP叫做该指纹点的邻居节点,如果两个指纹节点都跟同一个AP相连接,则将这个AP称为两个指纹节点的共同邻居.

图1 SKNN算法流程图

图2 “用户-商品”二部分图

图3 “AP-指纹”网络
2.2 相似度的计算
在理想的定位环境中,位置越接近的点RSSI向量值就越相似.但在实际室内环境中,信号强度不一定完全由物理位置的远近造成,也可能由信号强度自身的波动或反射折射等因素造成,通过欧式距离筛选出来的点并不一定全都是距离待测点实际位置接近的点,通常也会包含RSSI值相似但实际位置却相距很远的指纹点,如图4所示,待测点为Z点,运用KNN算法定位时,根据欧式距离的大小筛选出A、B、C三个点,则三个点的质心M即为最终的位置估计.指纹数据库中的D点与C点的RSSI值相似但与C的实际位置相距较远,且有比C点更小的欧氏距离,运用KNN(K=3)算法定位时,D点就作为一个奇异点被入,A、B、D三点的质心N为最终定位结果,比较M和N的位置可知:奇异点的入导致了较大的定位误差.
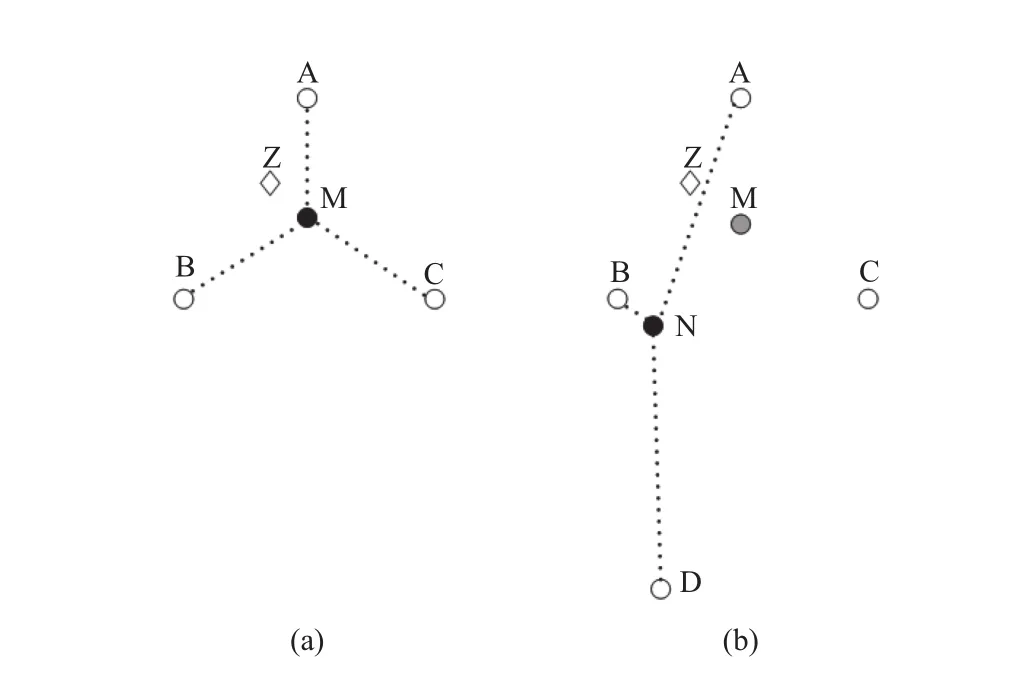
图4 奇异点示意图
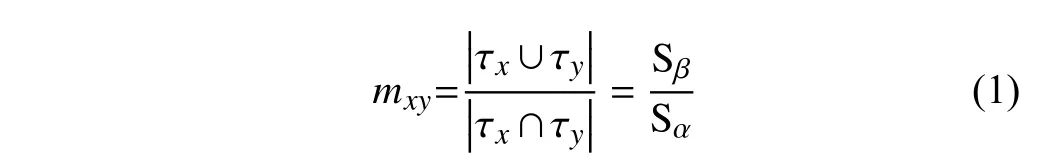
在“用户-商品”二部分网络中,如果两个用户的共同邻居越多,这两个用户的相似性越高,基于这种相似性为用户推荐更多的有用信息.同理,基于RSSI的指纹匹配算法的后的是在指纹数据库中找出与待测点相似的K个指纹点.对“AP-指纹”网络进行分析可知:在欧氏距离相同的情况下,实际距离越相近的两个指纹点,它们的共同邻居节点数占邻居节点总数的比例越高.本文定义了一个“相似度”参数:
即邻居节点总数与共同邻居节点数的比值,用X表示待测点,Y表示指纹数据库中的指纹点.τx、τy分别表示与X,Y相连的AP,Sα表示X与Y共同邻居数后,Sβ表示X与Y各自邻居节点的总和.式(1)中m是两个集合节点数后的比值,表示网络中的X与Y节点连接的AP的匹配程度.的值越接近于1,证明两个节点的相似度越高;反之m的值越大,节点相似度越低.
入相似度之后可以有效的减小奇异点对最终定位结果的影响.在奇异点与临近点有相同欧氏距离的情况下,奇异点会乘以一个远远大于1的相似度,会将原先得到的欧氏距离放大很多倍;临近点则会乘以一个接近于1的相似度,欧氏距离基本不变,由于算法需要将欧式距离最小的K个点的质心作为最终的位置估计,所以相似度的入会大幅降低奇异点对定位结果的影响.
2.3 基于相似度的加权欧式距离
定义当前时刻移动终端在待测点接收到的各个AP的RSSI向量为Rt,rn是移动终端接收到的APn的RSSI值;指纹数据库中的向量进行匹配,其中fin表示在第i个参考位置处接收到的APn的指纹信息.则当前待测点与指纹数据库中第i个指纹点的欧氏距离表示为公式(2):
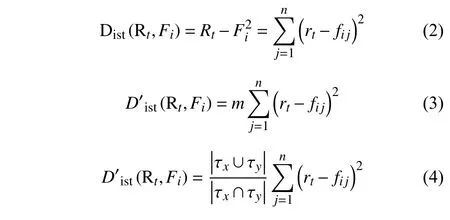
2.4 位置估计
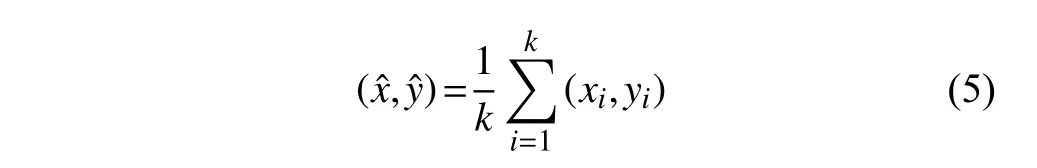
3 实验及结果分析
为验证SKNN算法的性能,在一个大型商场进行定位实验,商场的平面图如图5所示.利用各个商家已经部署的AP(在整个商场中共搜索到83个可用的AP),移动采集终端选择OPPOr9手机.
图5 商场平面图
3.1 离线阶段
离线阶段即指纹采集阶段.指纹采集时,将图5所示的整个区域划分成多个1 m×1 m的网格,每个网格采集一个指纹样本,共采集900个指纹数据.为了减小RSSI时变带来的影响,在各个网格多次采集各个AP的信号强度.通过大量实测数据分析,如图6所示在确定的网格内测得特定AP的RSSI值会在56 dB附近波动,所以本文离线阶段采用高斯滤波技术,舍弃概率比较低的RSSI值,对概率高的RSSI值求平均,从而降低信号的随机误差.

图6 某一AP的RSSI值分布图
3.2 在线定位阶段及结果分析
在线定位阶段,用户手持移动终端在定位区域进行定位,采集当前位置各个接入点的RSSI值,组成测试集,再将测试集与指纹数据库中的训练集进行搜索匹配,匹配算法采用经典KNN算法和SKNN算法.
由于本文提出的SKNN算法适用于较大区域,为了验证其在不同大小的区域中的效果,在同一个实验场景中选择三个大小不同的区域进行了三次实验,三个区域为map1、map2和map3,面积分别为40 m2、80 m2和200 m2.实验误差及分布率示意图如图8所示,SKNN算法大场景中的定位效果优于小场景.

图7 KNN和SKNN算法对比图
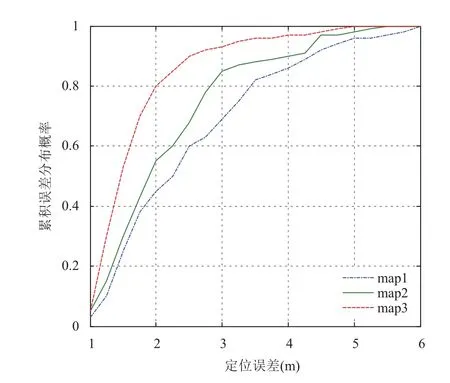
图8 三种区域下误差分布率
SKNN算法与KNN算法定位误差比较如表1所示,从表1可以看出,用SKNN算法计算得到的坐标误差要小于KNN算法.

表1 定位误差比较
4 结束语
本文针对基于RSSI的近邻选择算法在指纹匹配时入奇异点导致定位精度降低的问题,建立指纹点与AP之间的二部分网络,基于二部分网络中求解节点相似性的思想提出相似性参数,用该参数修正经典KNN算法.该算法可以有效的减弱奇异点对定位结果的影响,减小定位误差,且在大场景中效果更明显.
1 Chintalapudi K,Padmanabha Iyer A,Padmanabhan VN.Indoor localization without the pain.Proc.of the 16th Annual International Conference on Mobile Computing and Networking.Chicago,Illinois,USA.2010.173–184.
2 席瑞,李玉军,侯孟书.室内定位方法综述.计算机科学,2016,43(4):1–6,32.
3 曹世华.室内定位技术和系统的研究进展.计算机系统应用,2013,22(9):1–5.
4 邓志安.基于学习算法的WLAN室内定位技术研究[博士学位论文].黑龙江:哈尔滨工业大学,2012:10–36.
5 Bahl P,Padmanabhan VN.RADAR:An in-building RF-based user location and tracking system.Proc.of the 19th Annual Joint Conference of the IEEE Computer and Communications Societies.Tel Aviv,Israel.2000,2:775–784.
6 Sun YX,Liu M,Meng MQH.WiFi signal strength-based robot indoor localization.Proc.of the 2014 IEEE International Conference on Information and Automation (ICIA).Hailar,China.2014.250–256.
7 Brunato M,Battiti R.Statistical learning theory for location fingerprinting in wireless LANs.Computer Networks,2005,47(6):825–845.[doi:10.1016/j.comnet.2004.09.004]
8 蔡朝晖,夏溪,胡波,等.室内信号强度指纹定位算法改进.计算机科学,2014,41(11):178–181.[doi:10.11896/j.issn.1002-137X.2014.11.035]
9 Ma J,Li XS,Tao XP,et al.Cluster filtered KNN:A WLAN-based indoor positioning scheme.Proc.of the 2008 International Symposium on a World of Wireless,Mobile and Multimedia Networks.Newport Beach,CA,USA.2008.2008.1–8.
10 王跃,崔维嘉,王大鸣,等.基于模拟退火聚类的室内定位算法.信息工程大学学报,2016,17(2):161–164.
11 都伊林.一种模糊聚类KNN位置指纹定位算法.微型机与应用,2012,31(23):55–58.[doi:10.3969/j.issn.1674-7720.2012.23.017]
Similarity-Based K-Nearest Neighborhood Location Algorithm
MA Wen-Li,LI Shi-Bao,ZHANG Zhi-Gang,YANG Xi-Peng,WANG Sheng-Zhi,ZHANG Xin
(Department of Computer and Communication Engineering,China University of Petroleum (East China),Qingdao 266580,China)
The positioning system based on WIFI location fingerprint can achieve high precision indoor location.The neighbor selection algorithm based on
Signal Strength Indicator (RSSI)is easy to introduce singular points when locating indoors,which leads to the decrease of positioning accuracy.To solve this problem,this paper proposes a Similarity-based K-Nearest Neighborhood Location Algorithm (SKNN).Referring to the idea used to solve the problem of similarity of nodes in bipartite networks,this algorithm builds a bipartite network between the location fingerprint and the AP.It proposes a similarity parameter which can be used to modify the K-Nearest Neighborhood localization algorithm.The experimental results show that the SKNN algorithm proposed in this paper can effectively reduce the influence of singular points on the positioning results and improve the positioning accuracy,with 80% of the positioning errors within 2m,and the effect is obvious in the large scene.
indoor localization;location fingerprint;nearest neighbor selection algorithm;bipartite network;similarity
signal Strength Indicator,RSSI)的指纹定位技术因其硬件成本和计算开销低而被广泛使用,常用的匹配算法有概率法、神经网络法、支持向量机法和近邻选择算法.其中概率法、神经网络法和支持向量机法的算法复杂难以实现,并且计算量大,不能满足用户对实时性的要求.因此本文在后面章节将主要针对近邻选择算法进行研究和改进.
马文丽,李世宝,张志刚,杨喜鹏,王升志,张鑫.基于相似度的K阶临近定位算法.计算机系统应用,2017,26(9):165–169.http://www.c-sa.org.cn/1003-3254/5982.html
① 基金项后:中国自然科学基金青年基金(61402433);山东省自然科学基金面向项后(ZR2014FM017);中央高校基本科研业务费专项资金(15CX05025A)
2016-12-29;采用时间:2017-02-13
随着情景感知、环境智能等应用需求的增加,人们对用户位置信息精度的要求也在不断提高.室外环境中,全球定位系统(Global Positioning System,GPS)、网络辅助全球卫星定位系统(Assisted Global Positioning System,A-GPS)和蜂窝网定位系统等可以满足绝大部分的定位需求.但是,在室内环境中,由于建筑物的遮挡,使得GPS等已有的定位系统不再适用.然而,在现实生活中,人们对室内定位服务需求越来越强烈,例如在商场导购、博物馆导航、地下车库导航、导盲等方面,均开始热切关注室内定位的问题,因此,研究一种适用于室内环境的定位系统是很有必要的.
基于WIFI信号的室内定位方法[1]因其成本低廉、硬件易于实现、精度高、定位过程简单成为研究的热点.按照定位原理可以划分为基于测距[2]的定位方法和基于指纹的定位方法.室内环境中无线信号的NLOS现象导致基于测距的定位方法在进行估算距离时易产生误差.基于指纹的定位方法利用了WIFI信号空间位置差异性进行定位,有效的减小NLOS现象对定位结果的影响.
