再入飞行器的RCS控制系统设计①
2017-09-15郭建国张添保王国庆
郭建国,张添保,周 军,王国庆
(1.西北工业大学,精确制导与控制研究所,西安 710072;2.中国运载火箭技术研究院研发中心,北京 100076)
再入飞行器的RCS控制系统设计①
郭建国1,张添保1,周 军1,王国庆2
(1.西北工业大学,精确制导与控制研究所,西安 710072;2.中国运载火箭技术研究院研发中心,北京 100076)
针对再入飞行器初始再入段的发动机反作用控制系统(RCS)控制精度问题,提出了一种新型发动机控制方法。首先,将飞行器模型分为慢回路和快回路分别进行控制器设计,采用非线性干扰观测器(DOB)来获取不确定项的估计值,并使用反演法及滑模控制方法设计了飞行器的慢回路和快回路控制律;其次,采用线性规划方法来获取最优RCS指令分配方案;在此基础上,对传统PWPF调制器进行改进,提出了积分补偿型PWPF调制器(IPWPF),采用描述函数法证明了该IPWPF的调制稳定性;最后,通过仿真验证了该方法相比于传统的控制方法具有较高的控制精度。
再入飞行器;反作用控制系统;干扰观测器;滑动模态;脉冲调制器
0 引言
再入飞行器飞行包线大、航程远[1]。再入飞行初期,由于空气稀薄,需采用RCS控制[2-3];再入段中期,气动舵面能够提供一定的控制力矩,但控制效率较低,一般采用RCS/气动复合控制[4-5];再入段末期,空气比较稠密,可单独采用气动控制。本文研究再入飞行初期的RCS控制问题。
再入飞行器RCS的推力大小和方向不可调节,只能提供脉冲式控制量,而控制律提供的是连续控制信号。RCS喷气逻辑的设计是RCS控制的一大关键问题,国内外常用的方法是采用脉冲宽度调制器(PWM)来进行拟线性跟踪控制。然而传统的PWM只能调制脉冲宽度。为了使调制器既能调制脉冲宽度,又能调制频率,一些学者对传统的PWM进行了改进,提出了脉宽——频率调制器(PWPF)[5-6]。但是PWM和PWPF均只考虑了输入信号的大小与输出信号的脉冲宽度及频率,而没有考虑拟线性跟踪的精度问题。本文在PWPF的基础上,对其进行改进,提出了一种积分补偿型调制器(IPWPF),使其对信号的复现精度更高。
控制律的设计也是飞行器控制系统设计的一大关键问题。目前常用的控制方法有PID控制方法[7]、滑模控制方法[8-11]、鲁棒控制方法[12]和自适应控制方法[13]。由于再入飞行器模型具有强耦合、强非线性和快时变特性,PID控制方法很难满足鲁棒性要求;而鲁棒控制方法和自适应方法设计较为复杂,工程实现困难,故而滑模控制方法被广泛运用。本文采用滑模变结构控制思想设计了再入飞行器的控制律。对于飞行器模型中不确定项,采用非线性干扰观测器(DOB)[14-15]来进行估计。
RCS一般采用冗余喷管配置方案,其数目远大于飞行器自由度数目,为一个过驱动控制系统[16]。能完成同样的控制任务的推力器组合不止一种,而需寻求一种既能使控制精度最好,又能节省的控制组合。本文采用线性规划[1,17]的方法来进行推力器组合控制的优化分配。
1 再入飞行器运动模型
在文献[18]的基础上,可得再入初期飞行器运动方程:
(1)
式中Ω=[φV,β,α]T为飞行器的倾侧角、侧滑角和攻角;ω=[ωx,ωy,ωz]T为飞行器的滚转角速率、偏航角速率和俯仰角速率;M为RCS提供的控制力矩;f和φ为不确定项;非线性项g(ω)=I-1ω×(I·ω);A、B、I为系数矩阵。
本文研究10推力器RCS,其在机尾的布局见图1。
RCS控制系统的模型为
M=MRCSσ
(2)
其中
(3)
式中σ=[σ1,σ2,…,σ10]T为推力器的开启逻辑,σi=[0,1],i=1,2,…,10。
飞行器再入初期运动方程为
(4)
2 控制系统设计
2.1 非线性干扰观测器
飞行器飞行时,受到各种不确定项的作用,其中包括参数不确定和外部干扰。对这些不确定项,可采用干扰观测器(DOB)[19]对不确定项进行估计。含不确定项的飞行器的运动方程如式(4)所示。
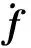
(5)
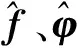
(6)
式中d1=2δf/min(λ1i),d2=2δφ/min(λ2i),i=1,2,3。
2.2 控制律设计
设Ωc=[φVc,βc,αc]T为指令信号,将飞行器控制系统分为慢回路和快回路进行设计。利用滑模控制方法,采用反演法[21]获取姿态角速率指令ωc作为快回路的虚拟控制信号,ωc=[ωxc,ωyc,ωzc]。设:
e1=Ωc-Ω
(7)
e2=ωc-ω
(8)
对式(7)和式(8)求导得
(9)
(10)
取慢回路滑模面为
s1=e1
(11)
式中s1=[s11,s12,s13]T。
采用指数趋近率:
(12)
式中K1=diag(k11,k12,k13),ε1=diag(ε11,ε12,ε13),且有k1i>0,ε1i>d1,i=1,2,3。
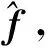
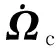
(13)
则在虚拟控制ωc的作用下,式(9)变为
(14)
取快回路滑模面为
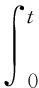
(15)
式中s2=[s21,s22,s23]T;C=diag(c1,c2,c3),且有ci>0,i=1,2,3;Γ=diag(γ1,γ2,γ3),且有γi>0,i=1,2,3。
对滑模面(15)求导得
(16)
趋近率取为
(17)
式中K2=diag(k21,k22,k23),k2i>0,i=1,2,3;ε2=diag(ε21,ε22,ε23),ε2i>d2,i=1,2,3。
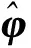
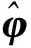
(18)
ωc中含有符号函数项,导致ωc不可导,需用滤波器来获得近似导数。设滤波方程为
(19)
式中T=diag(T1,T2,T3)为滤波器时间常数矩阵。
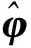
(20)
在控制σ的作用下,式(10)变为
(21)
设式(20)的右端项为U,则有
MRCSσ=U
(22)
由于σ∈R10×1,U∈R3×1,RCS控制要求燃料消耗最少,取性能指标:
(23)
约束条件为
s.t 0≤σi≤1
(24)
可采用线性规划方法进行优化求解指令σ。
定理1 对于式(4)所示的再入飞行器,采用式(13)作为慢回路虚拟控制量、式(22)的优化结果σ作为快回路控制量,使得姿态控制系统稳定。
证明 慢回路稳定性:设Lyapunov函数:
(25)
对式(25)求导,并将式(14)代入,则有
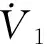
≤-min(k1i)‖e1‖2-min(ε1i-d1)‖e1‖
则慢回路稳定。
快回路稳定性:设Lyapunov函数:
V2=s2Ts2/2
(26)
其对时间的一阶导为
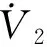
(27)
将式(18)代入式(27)是可得

≤-min(k2i)‖s2‖2-min(ε2i-d2)‖s2‖

(28)
取Lyapunov函数为
V3=e2Te2/2
(29)
则对其进行求导有
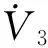
≤-min(ci)‖e2‖2-min(γi)‖e2‖
可见快回路稳定。
为了避免符号函数引起的控制信号高频颤振,本文采用饱和函数sat(x)代替符号函数sgn(x)。选择边界层Δ>0,饱和函数为
(30)
而对于式(20)的控制量σ,不是0-1信号,需采用PWPF调制器进行调制。
2.3 积分补偿型PWPF调制器设计
本文在文献[5-6]中PWPF的基础上进行了改进,设计了一种积分补偿型PWPF调制器(Integral Pulse-Width Pulse-Frequency Modulator, IPWPF),其原理图如图2所示。该PWPF调制器包括前置低通滤波器、施密特触发器、单位反馈回路和积分补偿回路。
图中,σ为待调制的控制信号,u为0-1式开关信号。记滤波器输入为e(t),输出为
f(t)=f(0)+[kme(t)-f(0)](1-e-t/τm) (31)
记开启时刻t=0,再次关闭时刻记为t=Ton,则f(0)=d,f(Ton)=d-h,因此满足
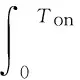
要使IPWPF调制器正常工作,IPWPF调制器的最小信号输入σmin需满足
km(kpσmin+kiσminTon)=d
(33)
联立式(32)及式(33) ,整理可得,最短开启时间满足
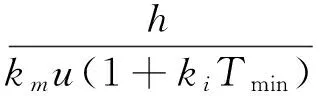
(34)
可选择合适的参数组合,用式(34) 来估算最短开启时间。若推力器开启最短时间为80ms,则可选取参数组合为:km=1,τm=0.16,d=0.6,h=0.4,kp=2.5,ki=10。
定理2 对于飞行器再入初期的RCS控制,采用图2所示的IPWPF调制器进行信号的调制,使得RCS调制系统稳定。
证明 对于非线性系统,一般采用描述函数法来分析稳定性。IPWPF调制器等效图如图3所示。
将非线性部分的描述函数记为N(A),并记线性环节为
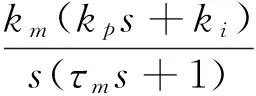
(35)
则闭环系统的特征方程为
1+N(A)G(jω)=0
(36)
其中,非线性环节描述函数为
(37)
作ΓG曲线和-1/N(A)曲线如图4所示,从图4中可见,ΓG曲线不包围-1/N(A)曲线,说明系统稳定。
证毕。
设IPWPF调制器的输入能量为Qσ,输出能量为Qu,定义:
(38)
取σ=0.8+0.2sin(πt+0.5),分别采用IPWPF调制器和传统PWPF调制器[6]进行调制,IPWPF调制器和传统PWPF调制器对能量的跟踪曲线如图5所示,对比可知,IPWPF调制器的能量跟踪能力明显优于传统PWPF调制器。
3 仿真验证
飞行器飞行高度为100 km,速度为7500 m/s。控制参数为:K1=diag(0.3,0.8,0.3),ε1=diag(0.15,0.15,0.1),C=diag(0.2,0.3,0.2),Γ=diag(0.02,0.15,0.02),K2=diag(0.4,1,0.4),ε2=diag(0.15,0.2,0.1),T=diag(0.1,0.1,0.1),Δ=0.2。非线性干扰观测器参数为:Λ1=diag(0.5,0.2,0.1),Λ2=(2,2,2)。取期望角度指令为:αc=10°,βc=0°,φVc=5°。采用本文DOB+IPWPF方法和传统PWPF分别进行仿真分析,其攻角、侧滑角和速度倾角跟踪曲线如图6~图8所示。由图6~图8知,在传统PWPF调制方法下,攻角跟踪稳态误差为2°,稳态侧滑角误差为1°,倾侧角跟踪稳态误差为2°。而采用本文DOB+IPWPF方法,攻角跟踪稳态误差为0.5°,稳态侧滑角误差为0.5°,倾侧角跟踪稳态误差为0.5°。由此可见,本文方法控制下,对姿态角跟踪的稳态性能优于传统PWPF,拟线性跟踪的精度比传统的PWPF高。从动态性能来看,两种方法的上升时间相当,动态性能相差不大。
图9为两种方法消耗的燃料对比图。由图9可见,本文RCS控制方法的燃料消耗量比传统PWPF方法要多。但燃料消耗可通过调节积分补偿系数ki来调节。ki越大,精度越高,燃料消耗越多;ki越小,精度越低,燃料消耗越少;合理地选取ki,使得控制既满足精度要求,又不至于消耗过多的燃料。
4 结论
(1)采用积分补偿型脉冲调制器(IPWPF)产生的RCS发动机开关逻辑指令,对输入信号进行拟线性跟踪,其跟踪精度优于传统的PWPF调制器。
(2)采用滑模变结构控制方法设计控制器,并利用非线性干扰观测器(DOB)对系统不确定项进行估计,将估计值作为控制系统的补偿量,使得控制器具有较强的抗干扰性能,控制精度更高。
[1] 贺成龙, 陈欣, 杨一栋. 一种动态逆解算的RLV混合规划控制分配研究[J]. 系统工程与电子技术, 2010, 32(9): 1973-1976.
[2] Zhou J, Ji P F, Hu W J. Attitude control algorithm for reusable launch vehicle in reentry flight phase [J]. Journal of China Ordnance, 2009, 5(1): 15-19.
[3] 房元鹏. 可重复使用航天器反作用力控制系统控制方法[J]. 航空学报, 2008, 29(增刊): S97-S101.
[4] David B D, Brian J G, Anhtuan D N. Quantized control allocation of reaction control jets and aerodynamic control surfaces [J]. Journal of Guidance, Control, and Dynamics, 2009, 32(1): 13-24.
[5] Geng J, Sheng Y Z, Liu X D. Finite-time sliding mode attitude control for a reentry vehicle with blended aerodynamic surfaces and a reaction control system [J]. Chinese Journal of Aeronautics, 2014, 27(4): 964-976.
[6] Wang X S, Wang D W, Zhu S Q, et al. Fractional describing function analysis of PWPF modulator[R]. Mathematical Problems in Engineering, 2013, 34(1): 130-137.
[7] Xu Z, Tang S. RLV (Reusable launch vehicle) reentry nonlinear controller design [C]//2010 International Conference on Computer, Mechatronics, Control and Electronic Engineering, Changchun, 2010: 380-383.
[8] 李宪强, 周军. 再入飞行器多约束姿态控制律设计[J]. 固体火箭技术, 2015, 34(4): 472-476.
[9] James E S, Yuri B S. Launch vehicle attitude control using higher order sliding modes[C]//AIAA Guidance, Navigation, and Control Conference, Toronto, 2010: 1-14.
[10] Sheng Y Z, Geng J, Liu X D, et al. Nonsingular finite-time second order sliding mode attitude control for reentry vehicle[J]. International Journal of Control, Automation, and System, 2015, 13(4): 853-866.
[11] 宋超, 赵国荣, 陈洁. 基于鲁棒滑模观测器的高超声速飞行器双环滑模控制[J]. 固体火箭技术, 2012, 35(4): 438-441.
[12] Cui L, Yang Y. Disturbance rejection and robust least-squares control allocation in flight control system [J]. Journal of Guidance, Control, and Dynamics, 2011, 34(6): 1632-1643.
[13] 王芳, 宗群, 田栢苓, 等. 基于鲁棒自适应反步的可重复使用飞行器再入姿态控制[J]. 控制与决策, 2014, 29(1): 12-18.
[14] Charles E H, Yuri B S. Sliding mode disturbance observer-based control for a reusable launch vehicle[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(6): 1315-1328.
[15] Chen X S, Yang J, Li S H, et al. Disturbance observer based multi-variable control of ball mill grinding circuits [J]. Journal of Process Control, 2009, 19(7):1205-1213.
[16] 黄頔, 郝宇清, 段志生. 可重复使用天地往返飞行器中的多输入控制问题[J]. 控制理论与应用, 2014,31(7): 878-889.
[17] 及鹏飞, 周军, 呼卫军. 可重复使用运载器再入段喷气选择逻辑重构研究[J]. 西北工业大学学报, 2007,25(6): 794-799.
[18] 李惠峰.高超声速飞行器制导与控制技术[M]. 北京:中国宇航出版社,2012.
[19] 刘宇超, 郭建国, 周军, 等. 基于新型快速Terminal滑模的高超声速飞行器姿态控制[J]. 航空学报, 2015, 36(7): 2372-2380.
[20] 张天翼, 周军, 郭建国. 基于干扰观测器的高速飞行器预测控制律设计[J]. 航空学报, 2014, 35(1): 215-222.
[21] 赵明元, 魏明英, 何秋茹. 基于有限时间稳定和Backstepping 的直接力/气动力复合控制方法[J]. 宇航学报, 2010, 31(9): 2157-2164.
(编辑:吕耀辉)
Reaction control system design for reentry vehicle
GUO Jian-guo1, ZHANG Tian-bao1, ZHOU Jun1, WANG Guo-qing2
(1.Institute of Precision Guidance and Control, Northwestern Polytechnical University,Xi'an 710072, China;2.China Academy of Launch Vehicle Technology, Beijing 100076, China)
According to the tracking error of reaction control system (RCS), a new precision control strategy is proposed for the initial reentry phase of reentry vehicle. Firstly, a nonlinear disturbance observer (DOB) is used for observing the model uncertainty and/or external disturbances. Secondly, a sliding mode control system for the fast loop and slow loop is designed by back-stepping style, and obtained the optimal combination of RCS by linear optimization. Besides, a Integral PWPF Modulator (IPWPF) is proposed based on traditional PWPF modulator, and its stability is proved by a describing function. Finally, the simulation indicates a great precision of the method.
reentry vehicle;reaction control system;disturbance observer;sliding mode;PWPF modulator
2016-11-18;
2016-12-27。
国家自然科学基金(61473226);航天创新基金(N14XW0001)。
郭建国(1975—),男,教授,研究方向为飞行器制导与控制。E-mail:guojianguo@nwpu.edu.cn
V448
A
1006-2793(2017)04-0511-06
10.7673/j.issn.1006-2793.2017.04.020
