基于NHDO的机动目标拦截攻击角度约束导引律①
2017-09-15雷虎民叶继坤
王 斌,雷虎民,李 炯,邵 雷,叶继坤
(空军工程大学 防空反导学院,西安 710051)
基于NHDO的机动目标拦截攻击角度约束导引律①
王 斌,雷虎民,李 炯,邵 雷,叶继坤
(空军工程大学 防空反导学院,西安 710051)
为了精确控制导弹在有限时间内以期望攻击角度拦截机动目标,采用将导弹自动驾驶仪简化为惯性环节的方法,结合终端滑模控制理论设计了一种带攻击角度约束的有限时间收敛制导律。为了滤除视线角速率噪声,提出一种非线性跟踪微分滤波器对噪声进行滤波,建立了考虑滤波的制导系统状态方程,基于此方程设计非齐次干扰观测器,用于目标机动不确定项的估计补偿。仿真结果表明,所设计的制导律能达到对视线角速率有效滤波,对目标机动状态精确估计的目的,克服系统动态延迟对制导精度的不利影响,满足攻击角度和制导精度的双重要求。
攻击角度约束;有限时间收敛;跟踪微分滤波器;非齐次干扰观测器;制导律
0 引言
导弹作为现代战争的主要作战武器,其制导精度始终是人们努力追求的优化目标,而以零化脱靶量为主要目的传统制导武器已不能满足最佳打击效果的战术要求。为取得最佳打击效果,最大程度地击毁目标,必须在高精度制导的同时考虑导弹命中目标时的姿态问题,即攻击角度约束问题[1]。无论是反舰导弹饱和攻击,还是反导拦截协同作战,都要求拦截弹从不同的方向以一定的攻击角度击中目标。因此,开展带攻击角度约束的制导方法研究具有现实而紧迫的意义。
伴随控制理论的不断发展,攻击角度约束的导引律(IACG)研究已经取得一系列丰硕成果。文献[2-3]讨论了一类两阶段控制的偏置比例导引律,用于攻击固定目标和非机动运动目标;文献[4]针对固定目标,提出一种时变比例导引系数的IACG;文献[5]将文献[4]的方案进一步改进,使其扩展到非机动运动目标的拦截上;文献[6]设计了一种虚拟角度控制项,将攻击角度控制问题转化为该虚拟量的收敛问题。上述导引律虽然实现了对攻击角度的精确控制,但只适合于拦截非机动目标,且没有考虑自动驾驶仪延迟对制导性能的影响。
对于同时考虑自动驾驶仪延时和攻击角度约束的问题,文献[7]基于线性化导引模型提出了一种新的非线性滑模导引律,但同样只针对静止或低速目标;文献[8-9]基于反演动态面控制理论设计了拦截机动目标的IACG,但采用估计目标机动上界的办法有失一般性,且估计值的准确与否直接影响制导性能;文献[10]设计了拦截机动目标的积分滑模IACG,并采用高阶滑模微分器估计目标加速度;文献[11]同样采用积分滑模设计IACG,不同之处在于其应用干扰观测器估计目标加速度;文献[12]引入扩张状态观测器估计目标机动扰动,并以此设计了非奇异终端滑模IACG。需要说明的是,上述文献所采用的观测器只能保证观测误差渐近收敛,而非有限时间收敛,且所有关于自动驾驶仪延时的IACG研究均未考虑视线角速率量测噪声。
针对考虑自驾动态特性和视线角速率噪声的机动目标拦截攻击角度约束问题,本文利用线性滑模面结合非奇异终端滑模控制的方法设计了一种有限时间收敛IACG。为了抑制量测噪声,设计一种跟踪微分滤波器进行滤波;为了对目标机动干扰进行补偿,采用误差有限时间收敛的非齐次干扰观测器对其精确估计。仿真结果表明,所设计导引律在噪声抑制、干扰估计、制导精度和落角偏差方面都具有十分优异的性能。
1 制导模型描述
1.1 弹目相对运动方程
末制导过程的弹目相对运动是俯仰平面和偏航平面的耦合运动,本文为了研究方便,将其简化为两个通道的独立运动,考虑到俯仰平面与偏航平面运动的相似性,因此本文只研究二维俯仰平面的弹目相对运动,如图1所示,相对运动方程如下:
(1)
(2)
(3)
(4)
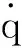
对式(2)求导可得
(5)
整理可得
(6)

(7)
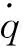
1.2 考虑自动驾驶仪动态特性含攻击角度约束的制导模型
定义弹目遭遇时刻导弹速度矢量与目标速度矢量之间的夹角为攻击角。设弹目遭遇时刻为tf,此时导弹和目标的弹道倾角分别为θMf、θTf,视线倾角为qf。基于零化视线角速率的思想,结合式(2)可得,在弹目遭遇时刻各倾角之间有以下关系成立:
VMsin(qf-θMf)=VTsin(qf-θTf)
(8)
期望攻击角φd为定值按式(9)计算:
φd=θMf-θTf
(9)
考虑到在末制导过程中导引头要锁定目标,因此目标要始终处于导引头的视场范围内[13],而对导引头视场角约束可通过对前置角的限制来处理,这里假定:
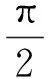
(10)
由式(8)~式(10)就可将弹目遭遇时刻期望攻击角φd转化为期望终端视线角qf来约束。
在导弹攻击目标的制导过程中,导弹自动驾驶仪的动态特性是影响制导精度的一个主要因素[13]。为避免其造成制导精度下降,在建立含攻击角度约束的制导模型时,将导弹自动驾驶仪近似为一阶惯性环节,反映在时域里,即
(11)
式中τ为延迟常数;u为提供给导弹的垂直视线方向的加速度指令。
(12)
(13)
对式(12)求导,并将式(11)代入得
(14)
将式(13)代入式(14)整理得
(15)
(16)
2 考虑滤波的目标机动状态估计
2.1 跟踪微分滤波器设计
为得到纯净的制导信息,有必要对含有噪声的视线角速率信号进行滤波处理。本节将利用跟踪微分器的噪声抑制能力,设计更加精确的跟踪微分滤波器。
非线性跟踪微分器的一般表达式为
(17)
式中v为带噪声的输入信号;μ1为滤波之后的跟踪信号;μ2为滤波之后的微分信号;γ为调节参数。
针对如下一阶微分方程:
(18)
若式(18)有精确解y=y(x),且y(x)是n+1阶连续可导,则y(x)可由泰勒公式展开为如下无穷级数:

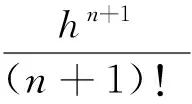
(19)
式中h为仿真步长,xk<ξ 如果令n=2,并且忽略高阶无穷小项,可得式(18)的泰勒近似求解表达式,即 (20) 由式(20)得式(17)的输出预测表达式为 (21) 将式(21)纳入式(17),可得所设计的跟踪微分滤波器表达式为 (22) 由于式(22)的第二式含有符号函数,在实际应用中可能会带来系统抖振,影响滤波性能。而连续光滑的双曲正切函tanh(x)取值无限趋近于±1,因此可采用双曲正切函数tanh(s(x,t)/d)对符号函数进行连续化处理,其中边界层厚度Δ=2πd[15]。 最终可得连续化后的跟踪微分滤波器的表达式: (23) 2.2 基于状态滤波的NHDO设计 为了对系统不确定性扰动进行跟踪估计,文献[14]基于非齐次微分器首次提出了可缩短暂态过程的非齐次干扰观测器,它能在保证误差有限时间收敛的同时提供最优的渐进精度。对于如下SISO非线性系统: (24) 式中u为系统控制输入u∈R;g(t)为m-1次可导连续不确定函数,且gm-1(t)具有Lipschitz常数L。 则针对系统(24)可设计如下有限时间收敛非齐次干扰观测器: (25) 其中,函数hi的表达式如下: 其中,λi>0,γi>0,i=0,1,2,…,m。 (27) 将2.1节所设计的跟踪微分滤波器扩张到系统(27)中去,可得如下包含滤波的制导系统状态方程: (28) 为了得到干扰f1*的Lipschitz常数,首先给出如下假设: 假设2[15]:系统(28)中时变弹目距离R满足R≥Ro,Ro为导引头盲区距离。在导引头盲区内,导引头不产生制导指令,导弹依靠惯性飞行。 结合假设1和假设2,干扰f1*的Lipschitz常数可由下式产生 (29) 式中VTmax、VMmax分别为目标和导弹的最大速度。 结合式(25)、式(26)可知,针对滤波后的制导系统(28),用于估计f1的非齐次干扰观测器应设计为 (30) 根据文献[16]的结论,系统经过有限时间的暂态过程之后,一定有下列等式成立: (31) 3.1 导引律设计 为了能使系统状态在弹目交会前极短的时间内实现快速收敛,本节将利用线性滑模面和Terminal滑模控制相结合的办法设计带有攻击角度约束的有限时间收敛制导律FSMG。 针对非线性制导系统(28),取so=αoμ3+μ4,为保证在有限时间达到滑模面so,设计一种具有递归结构的非奇异Terminal滑动模态为 (32) 其中,βo>0且1<ξ<2。 对式(32)求导可得: (33) 为确保滑动模态可达,选取如下快速幂次趋近律推导控制器: |s1|ηsgn(s1) (34) 其中,α1>0,α2>0,0<η<1。 由式(33)、式(34)可得制导指令: αoμ5-fo-f1)/b (35) 用观测器(30)的输出z1代替式(35)中的f1,并用2.1节所设计的跟踪微分滤波器滤除视线角速率噪声,得到最终可实现的有限时间收敛制导律为 βo-1ξ-1-αoμ5-fo-z1)/b (36) 3.2 收敛时间及稳定性分析 为证明导引律(35)作用下的制导系统有限时间收敛特性,首先给出如下Lyapunov有限时间稳定引理。 (37) 证明:将指令(35)代入式(33)有 αox3-fo-f1)=-α1s1-α2|s1|ηsgn(s1) (38) 取Lyapunov函数V=s12/2,对V求导并将式(38)代入得 |s1|η+1 其中,α1>0,α2>0,因为0<η<1,故0.5<(η+1)/2<1,满足引理1条件,因此所设计的导引律是有限时间收敛的,且收敛时间上界满足: (40) 同理可证在制导律(36)作用下的闭环导引系统也是有限时间收敛的。 Case1:不同期望视线角对比仿真 (1)不加视线角速率噪声 仿真条件为:导弹速度大小VM=1000 m/s,初始弹道倾角θM=60°,初始位置(XM,YM)为(0,0);目标速度大小VT=680 m/s,初始航迹角θT=190°,初始位置(XT,YT)为(10 000,10 000),为验证本文设计的攻击角度约束制导律对机动目标的拦截能力,设目标以大小为5g的法向加速度正弦机动,即αT=50 sin(πt/3)m/s2。制导律参数设置为αo=1.5,α1=α2=10,βo=25,ξ=1.85,η=0.7;干扰观测器参数设置为λo=8,λ1=5,λ2=3,γo=12,γ1=11,γ2=10,L=1.5;自动驾驶仪延时常数τ=0.5 s,制导指令周期取为10 ms,拦截弹过载限制为±30g。仿真如图2~图7和表1所示。 期望视线角/(°)脱靶量/m拦截时间/s实际视线角/(°)300.07439.650030.1341400.03079.372040.0069500.03539.382050.0057600.05989.615059.9644 分析图4~图6可知,针对不同的期望视线角,本文所设计的制导律都能保证滑模面在弹目交会前收敛于零,进而使视线角速率收敛到零,终端视线角达到期望角,证明了该制导律良好的有限时间收敛特性。而由表1数据可知,FSMG不仅落角偏差小,且脱靶量不超过0.1 m,满足高精度制导要求,说明其在拦截机动目标时的有效性。 由图7可看出,这种有效性是基于所设计的非齐次干扰观测器对目标机动干扰的精确估计,虽然导弹初始段需用法向过载较大(图3),但随着干扰估计精度的提高和滑模面的收敛,导弹法向过载呈逐渐减小的趋势,且在制导末段趋近于零,这样导弹可在制导初始段充分利用其机动能力调整攻击角度以及应对目标机动,制导末段则以较小的过载保证制导精度。 (2)加视线角速率噪声 为了验证2.1节设计的跟踪微分滤波器的有效性,给视线角速率加0.01 rad/s的高斯白噪声。设期望视线角为50°,跟踪微分滤波器参数设置为γ=1.5,d=0.005,其余仿真条件同(1)。则一次滤波效果如图8、图9所示。 为进一步说明滤波器的有效性,在视线角速率加0.01 rad/s高斯白噪声的情况下对30°、40°、50°、60°的期望视线角各做200次蒙特卡洛仿真,并计算脱靶量、视线角的均值和方差,结果如表2所示。 由图8、图9可看出,在保证视线角速率收敛的总体趋势下,本文所设计的跟踪微分滤波器能有效滤除干扰噪声,使终端视线角更加接近期望角。另外由表2也可看出,针对不同的期望视线角,脱靶量均值几乎不会超过0.1 m,视线角误差不会超过1°,且方差均维持在零左右,进一步证明了跟踪微分滤波器滤波的稳定性。 Case2:不同制导律对比仿真 为进一步说明本文设计的FSMG的优越性,将其与文献[18]提出的基于反步法的考虑目标机动和自动驾驶仪动特性的终端角度约束滑模导引律BSMG进行50°角约束下仿真对比,仿真条件同(1),仿真结果如图10~图13所示。 表2 200次蒙特卡洛仿真视线角统计特性 由仿真结果可看出,整体而言,FSMG和BSMG都具有良好的有限时间收敛特性,能满足机动目标拦截时的攻击角度约束要求。但具体来看,FSMG视线角速率能收敛至零且始终维持于零,而BSMG的视线角速率最终收敛在0.2 (°)/s附近(图12);在视线角的控制精度上,FSMG也比BSMG更加接近50°(图13),这主要是因为FSMG滑模面的收敛精度要高于BSMG(图11),在收敛速度方面,FSMG也要快于BSMG,尽管FSMG的法向过载稍大于BSMG,但始终在导弹可用过载范围内。而基于反步法设计的BSMG制导律不仅形式复杂,且易造成虚拟控制项的微分膨胀问题,相比之下,FSMG制导律形式简单,更适合工程应用。 本文采用线性滑模面和终端滑模控制理论设计了一种考虑自动驾驶仪动态特性的有限时间收敛攻击角度约束导引律。为滤除视线角速率噪声,设计了一种跟踪微分滤波器,建立了包含滤波的导引方程;针对目标机动带来的不确定性扰动,设计非齐次干扰观测器对其进行精确估计,并在制导律中加以补偿,仿真结果表明: (1)所设计的跟踪微分滤波器具有良好的滤波特性,能有效克服视线角速率噪声对制导精度的不利影响; (2)采用非齐次干扰观测器能够在有限时间内对目标扰动快速跟踪估计; (3)采用线性滑模面和终端滑模相结合的方法设计的有限时间收敛导引律能够满足攻击角度约束要求,克服导弹动态延迟影响,且导引律形式简单,易于工程实践。 [1] 蔡洪,胡正东,曹渊.具有终端角度约束的导引律综述[J].宇航学报,2010,31(2):315-323. [2] Erer K S,Merttopçuoɡlu O. Indirect impact-angle-control against stationary targets using biased pure proportional navigation[J].Journal of Guidance,Control, and Navigation,2012,35(2):700-703. [3] Erer K S,Özgören M K. Control of impact angle using biased proportional navigation[C]//AIAA Guidance,Navigation,and Control(GNC) Conference,2013:1-15. [4] Ratnoo A,Ghose D. Impact angle constrained interception of stationary targets[J].Journal of Guidance,Control, and Navigation,2008,31(6):1816-1821. [5] Ratnoo A,Ghose D. Impact angle constrained guidance against nonstationary nonmaneuvering targets[J].Journal of Guidance,Control, and Navigation,2010,33(1):269-275. [6] Zhang Y A,Ma G X,Wu H L. A biased proportional navigation guidance law with large impact angle constraint and the time-to-go estimation[J].Proceedings of the Institution of Mechanical Engineers,Part G: Journal of Aerospace Engineering,2014,228(10):1725-1734. [7] Lee C H,Kim T H,Tahk M J. Design of impact angle control guidance laws via high -performance sliding mode control[J].Proceedings of the Institution of Mechanical Engineers,Part G: Journal of Aerospace Engineering,2012,227(2):235-253. [8] 曲萍萍,周荻.考虑导弹自动驾驶仪二阶动态特性的导引律[J].系统工程与电子技术,2011,33(10):2263-2267. [9] 张尧,郭杰,唐胜景,等.机动目标拦截含攻击角约束的新型滑模制导律[J].兵工学报,2015,36(8):1143-1157. [10] Zhang Z,Li S,Luo S. Terminal guidance laws of missile based on ISMC and NDOB with impact angle constraint[J].Aerospace Science and Technology,2013,31(1):30-41. [11] Zhang Z X,Li S H,Luo S. Composite guidance laws based on sliding mode control with impact angle constraint and autopilot lag[J].Transactions of the Institute of Measurement and Control,2013,35(6):764-776. [12] Xiong S,Wang W,Liu X,et al. Guidance law against maneuvering targets with intercept angle constraint[J].ISA Transactions,2014,53(4):1332-1342. [13] 周慧波.基于有限时间和滑模理论的导引律及多导弹协同制导研究[D].哈尔滨:哈尔滨工业大学,2015. [14] Shtessel Y B,Shkolnikov I A,Levant A. Smooth second-order sliding modes: missile guidance application[J].Automatic,2007,43(8):1470-1476. [15] 马克茂,贺风华,姚郁.目标机动加速度的估计与导引律实现[J].宇航学报,2009,30(6):2213-2219. [16] Levant A. Non-homogeneous finite-time-convergent differentiator [C]//Preceedings of Decision and Control,2009 held jointly with the 2009 28th Chinese Control Conference. CDC/CCC 2009.Proceedings of the 48th IEEE Conference on. IEEE,2009:8399-8404. [17] Yu S H,Yu X H,Shirinzadeh B,et al. Continuous finite-time control for robotic manipulators with terminal sliding mode[J].Automatica,2005,41(11):1957-1964. [18] 孙胜,张华明,周荻.考虑自动驾驶仪动态特性的终端角度约束滑模导引律[J].宇航学报,2013,34(1):69-78. (编辑:吕耀辉) NHDO-based impact angle control guidance law for maneuvering target WANG Bin, LEI Hu-min, LI Jiong, SHAO Lei, YE Ji-kun (Air and Missile Defense College, Air Force Engineering University, Xi'an 710051, China) In order to control the missile to attack the maneuvering target with desired terminal impact angle precisely in finite time, finite time convergence guidance law based on terminal sliding mode control theory is proposed according to simplified autopilot lag by the first order inertial element. To filter the noise of the LOS rate, a nonlinear tracking differential filter is proposed and the state equation of the guidance system is constructed considering filtering. Meanwhile, a non-homogeneous disturbance observer is devised based on the equation of state proposed to track and estimate the target maneuver disturbance. Simulation results show that the proposed guidance law can achieve the aim of filtering the LOS rate noise, precisely tracking the maneuver state of the targets, eliminating the adverse effect caused by the dynamic delay, satisfying the requirements of terminal impact angle and guidance precision. lmpact angle constraint;finite time convergence;tracking differential filter;non-homogeneous disturbance observer;guidance law 2016-11-25; 2017-01-10。 国家自然科学基金(61573374;61503408);航空科学基金(20150196006)。 王斌(1993—),男,硕士生,研究方向为飞行器制导与控制。E-mail:wwbb125100@qq.com V448 A 1006-2793(2017)04-0517-08 10.7673/j.issn.1006-2793.2017.04.021
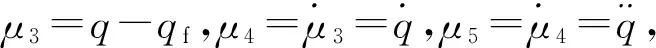



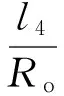
3 有限时间收敛导引律
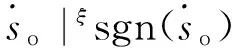
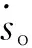



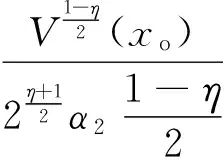
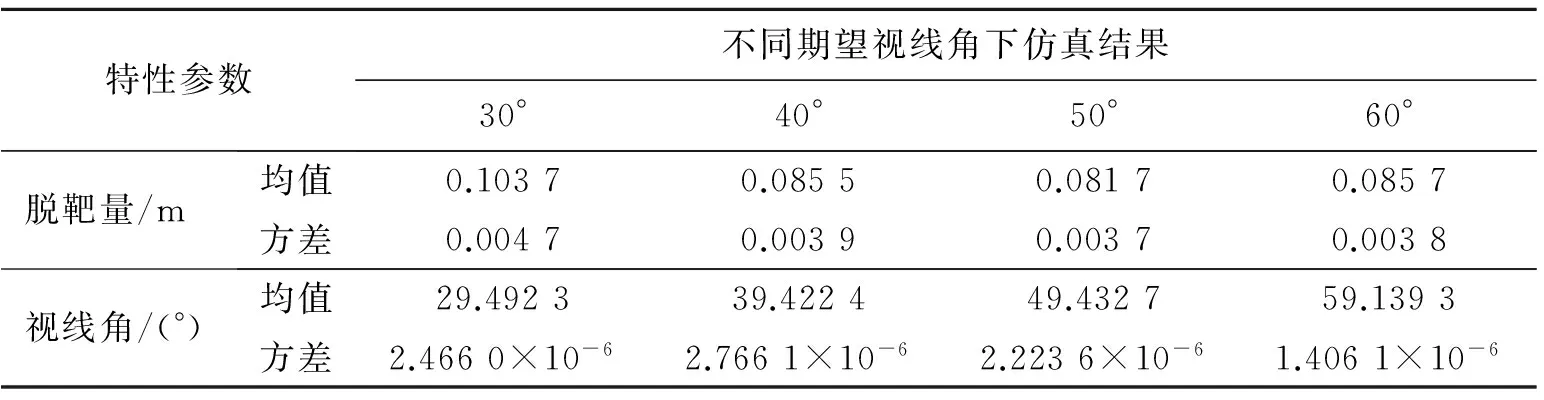
4 仿真实例与分析

5 结论
